考虑非局部应变梯度效应的轴对称压电纳米圆板热-力-电耦合振动

罗秋阳 李成

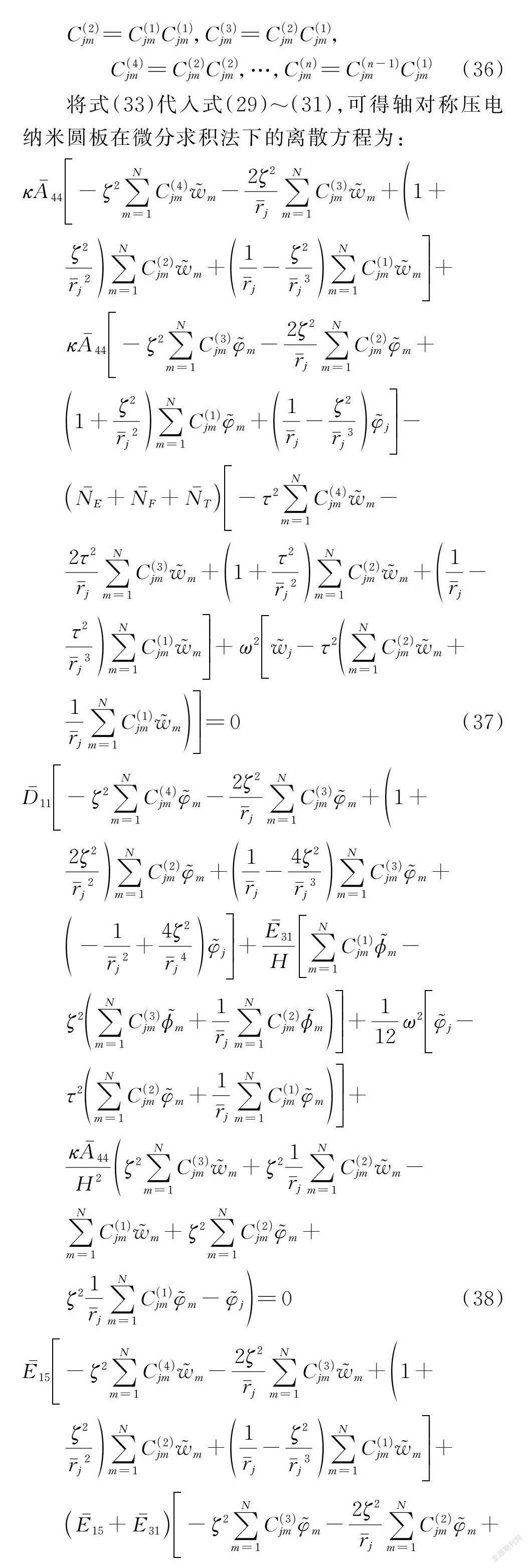
摘要：基于非局部应变梯度理论和Mindlin板理论，研究了热⁃力⁃电多场耦合下轴对称压电纳米圆板的振动特性。通过 Hamilton 原理推导了非局部应变梯度本构框架内的运动方程，采用微分求积法数值求解了理论模型微分方程组，分析了压电纳米圆板的振动固有频率受内尺度参数与外场参数的影响。压电纳米圆板的固有频率随着非局部参数的增大而减小，随着应变梯度特征参数的增大而增大。当非局部参数小于应变梯度特征参数时，纳米圆板表现出刚度硬化行为；当非局部参数大于应变梯度特征参数时，表现出刚度软化行为。当非局部参数等于应变梯度特征参数时，纳米圆板的刚度退化为相应的经典连续介质理论结果。此外，固有频率随着径向压力和正电压的增大而减小，随着径向拉力和负电压的增大而增大，随着温差的增加而小幅减小。特别地，研究发现当径向载荷和电压增大到一定程度时，纳米圆板出现了振动失稳现象，并分析了非局部参数与应变梯度特征参数对失稳临界径向载荷及临界电压的影响。

关键词：耦合振动；压电纳米圆板；非局部应变梯度；Mindlin板理论；轴对称

中图分类号： O326；O343.1    文献标志码： A    文章编号：1004-4523（2022）05-1118-12

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.009

引言

近年来，各种压电材料和结构成为研究热点[1⁃4]。当尺寸减小到纳米量级时，压电纳米材料和结构因为具有优越的热、电、机械、物理和化学性能，使其在纳机电系统中有着广泛的应用。研究压电纳米结构的力学性能对于纳机电系统的设计、调控及优化具有重要意义。

大量研究表明，当微结构处于纳米尺度时，其力学性能将呈现明显的尺度效应[5⁃6]。此时经典连续力学理论无法适用，因此需要发展纳米尺度下的新的理论与方法[7⁃8]。建立和发展能准确描述纳米结构尺度效应的非经典连续介质理论是当前纳米力学的研究前沿之一。其中，由 Lim 等[9]提出的非局部应变梯度理论，考虑了纳米材料和结构的非局部效应和应变梯度效应，是近年来应用最广泛的非经典连续介质理论[10⁃12]。Mehrez等[10]推导了弹性地基上非局部应变梯度石墨烯片的振動控制方程，探究了磁场、弹性基础、纳米粒子数量和质量、非局部参数以及应变梯度特征参数等对石墨烯片振动特性的影响。Wu 等[11]基于非局部应变梯度理论和改进的双曲剪切变形梁理论，建立了尺寸不均匀梁模型，研究了在外加谐波激励下，功能梯度增强复合纳米梁的非线性振动。Gholipour等[12]研究了非线性非局部应变梯度理论下的功能梯度 Timoshenko 纳米梁模型，并分析其动力学特性。基于非局部应变梯度理论，既考虑非局部效应又考虑应变梯度效应，所以模型和结果更为全面[13⁃19]。因此，本文以非局部应变梯度理论作为主要研究方法。

随着纳米技术的发展，压电纳米材料被认为有可能实现纳机电系统的自供电。王中林[20]采用氧化锌纳米线阵列作为纳米发电机部件，当作用5 nN的外力时，输出6.5 mV 的电压，在纳尺度下将机械能转化为电能。Motezaker等[21]基于高阶非局部理论研究了在顶部和底部表面集成了压电层的环形纳米板的振动、屈曲和弯曲。Eltaher等[22]考虑非局部效应与表面效应，研究了压电多孔纳米梁弯曲和自由振动，探讨了各类因素对压电多孔纳米梁的机电性能的影响。Karimiasl等[23]通过非局部理论推导了嵌入黏弹性地基中的磁电黏弹性压电纳米板在湿热环境下的控制方程组，并求出其临界载荷的解析解。

不过，尽管已有部分学者对压电纳米结构的振动开展了若干研究，但大多数文献是基于非局部理论，仅少数文献[24⁃25]考虑了非局部应变梯度效应。Arefi等[24]基于非局部应变梯度理论与各类高阶剪切变形梁理论推导了夹层压电纳米梁的控制方程，分析了动态失稳区域特征。Masoumi等[25]研究了挠曲电现象对压电纳米梁色散特性的影响，考虑 Reddy 高阶剪切变形理论以及非局部应变梯度理论推导控制方程，分析了挠曲电效应和施加电压对色散的作用。已有一些研究基于非局部应变梯度理论分析压电纳米梁模型，然而对纳米圆板模型的研究未见报道。考虑到纳米圆板作为纳机电系统的结构之一，常工作于多物理场环境中。因此，本文基于非局部应变梯度理论，研究在热⁃力⁃电多场作用下轴对称压电纳米圆板的振动特性，分析了非局部参数、应变梯度特征参数以及热⁃力⁃电场耦合对压电纳米圆板振动的影响。当然，纳米尺寸结构还存在表界面效应问题。以纳米圆板为例，当径厚比超过50时，纳米圆板的表界面效应不可忽略[26]。本文利用Mindlin板理论研究中厚纳米圆板，其径厚比不低于20，此时相比于表界面效应，非局部效应和应变梯度效应占主导地位。

1 力学模型与基本方程

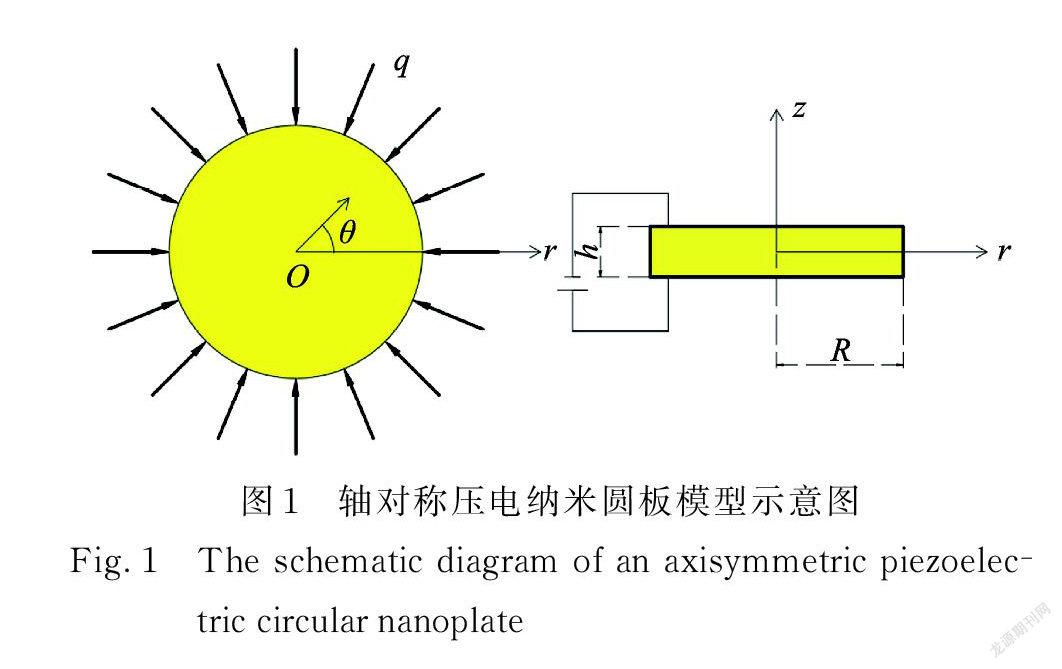
压电纳米圆板模型如图1所示，其中半径为 R，厚度为 h，受到径向均布载荷 q（单位：N/m）、外部电势Φ（单位：V）和温差ΔT（单位：K ）的作用，外边界约束考虑为常见的简支和固支两类。

根据非局部应变梯度理论，计及压电效应的基本方程为[27]：

式中σij，ε kl，Di 和Em分别表示应力、应变、电位移以及电场；cijkl，emij和 sim 分别表示弹性模量、压电常数和电介质常数；ea和 l 表征了非局部效应和应变梯度效应的影响；[·]表示矩阵，{·}表示数列。拉普拉斯算子∇2=∂2∂r2+∂ r∂r。

将基本方程引入到纳米圆板模型中可得其本构方程为：

其中：

对式（2）积分，且考虑柱坐标系下的圆板几何方程ε r = z ，εθ= z ，γrz =φ+，可得：

剪力弯矩；κ=为剪切修正因子，其余系数如下：

根据Mindlin板理论，轴对称纳米圆板的径向位移ur和横向位移uz可表示为：

式中  w （r，t ）表示圆板中面上任意一点的横向位移，φ（r，t ）表示圆板中面法线的转角，t 为时间变量。

假设电势由线性函数和正弦函数组成且满足Maxwell 方程[28]：

式中 β=π/h，ϕ（r，t ）表示圆板中面上任意一点的电势，V0为外部电压。

则电位移与电场的关系为：

通过 Hamilton 原理可推得轴对称压电纳米圆板的振动控制方程，即：

式中  U，T 和 K 分别表示系统的应变能、动能和外力做功。

轴对称压电纳米圆板的应变能可表示为：

则应变能变分为：

轴对称压电纳米圆板的动能可表示为：

则动能变分为：

其中：

式中ρ为圆板的体密度。

外力做功为：

则外力做功的变分为：

式中 NE =-2 31 V0，NF = q，NT =11 hΔT。

将式（12），（14）和（17）代入式（10），可得轴对称压电纳米圆板的经典控制方程为：

引入以下无量纲量：

式中  2表示无量纲化的拉普拉斯算子。

式（25）～（27）中，设其解为：

边界条件为：

2  求解方法

轴对称压电纳米圆板的振动控制方程组包含三个四阶偏微分方程，本文采用微分求积法进行数值求解。微分求积法的本质是对全域范围内所有节点的函数值进行加权求和，以表示该函数及其导数在所选节点的值。函数 W 的 n 阶导数可近似为：

式中ξm 为域中第 m 个节点，N 代表域中的节点数， C m（n））为 n 阶导数的加权函数。这里用切比雪夫多项式作为节点的选取方式，可得：

权系数表示为：

高阶导数可以看成对一阶导数的求导，于是有：

将式（33）代入式（29）～（31），可得轴对称压电纳米圆板在微分求积法下的离散方程为：

式中 j =2，3，…，N -1。

将方程（37）～（39）结合边界条件，可得特征方程为：

式中 K，M 分别为刚度矩阵和质量矩阵，下标 d 表示控制方程，下标 b 表示边界条件；q 表示节点位移： q 1={w͂ 1，w͂ 2，…，w͂ N }T，q2={ 1，2，…， N }T，

3 數值结果与讨论

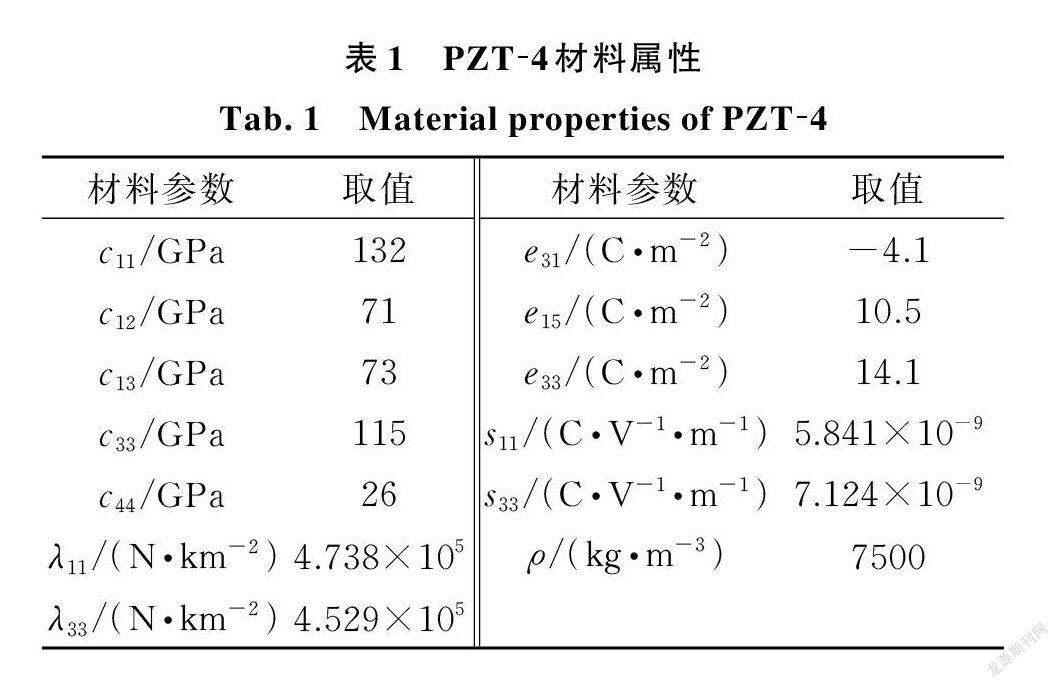
考虑厚度为2.5 nm ，半径为50 nm ，采用 PZT ⁃4材料做成的压电纳米薄板，材料参数如表1 所示。在计算中选取节点数 N=18，研究外边固支（C）、外边简支（S）两种边界下压电纳米圆板的振动特性，探索非局部参数、应变梯度特征参数、径向均布载荷、电场和温度场对无量纲固有频率的影响。

根据文献[29⁃30]，用于制备纳米圆板的常用材料的非局部参数ea一般不超过2 nm ，因此 PZT ⁃4材料的非局部参数也应在[0，2 nm]范围内，应变梯度本征常数 l 也相应地取在[0，2 nm]范围。

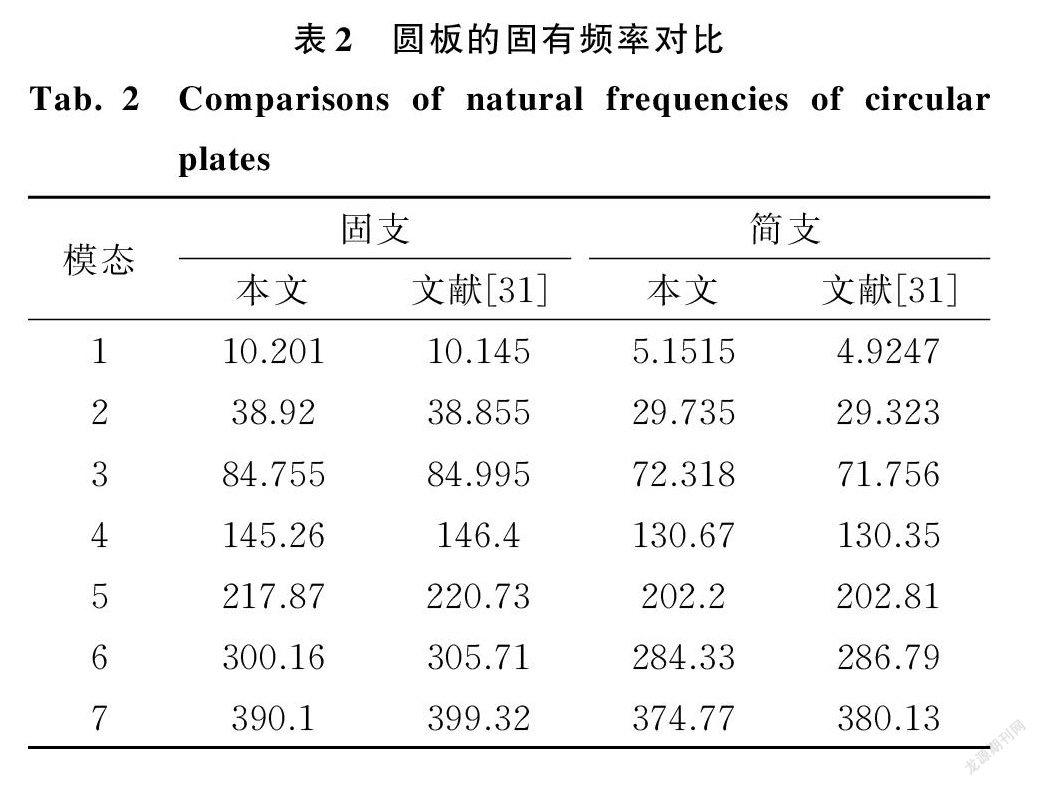
为了验证上述计算结果的准确性，将理论模型退化为宏观尺寸圆板的自由振动。结合边界条件，计算了外边固支和简支情况下宏观圆板的前7阶固有频率，并与文献[31]进行对比，如表2所示。从表2可见本文中的结果与文献[31]中的结果非常接近，因此验证了本文数值方法的有效性和数值结果的准确性。

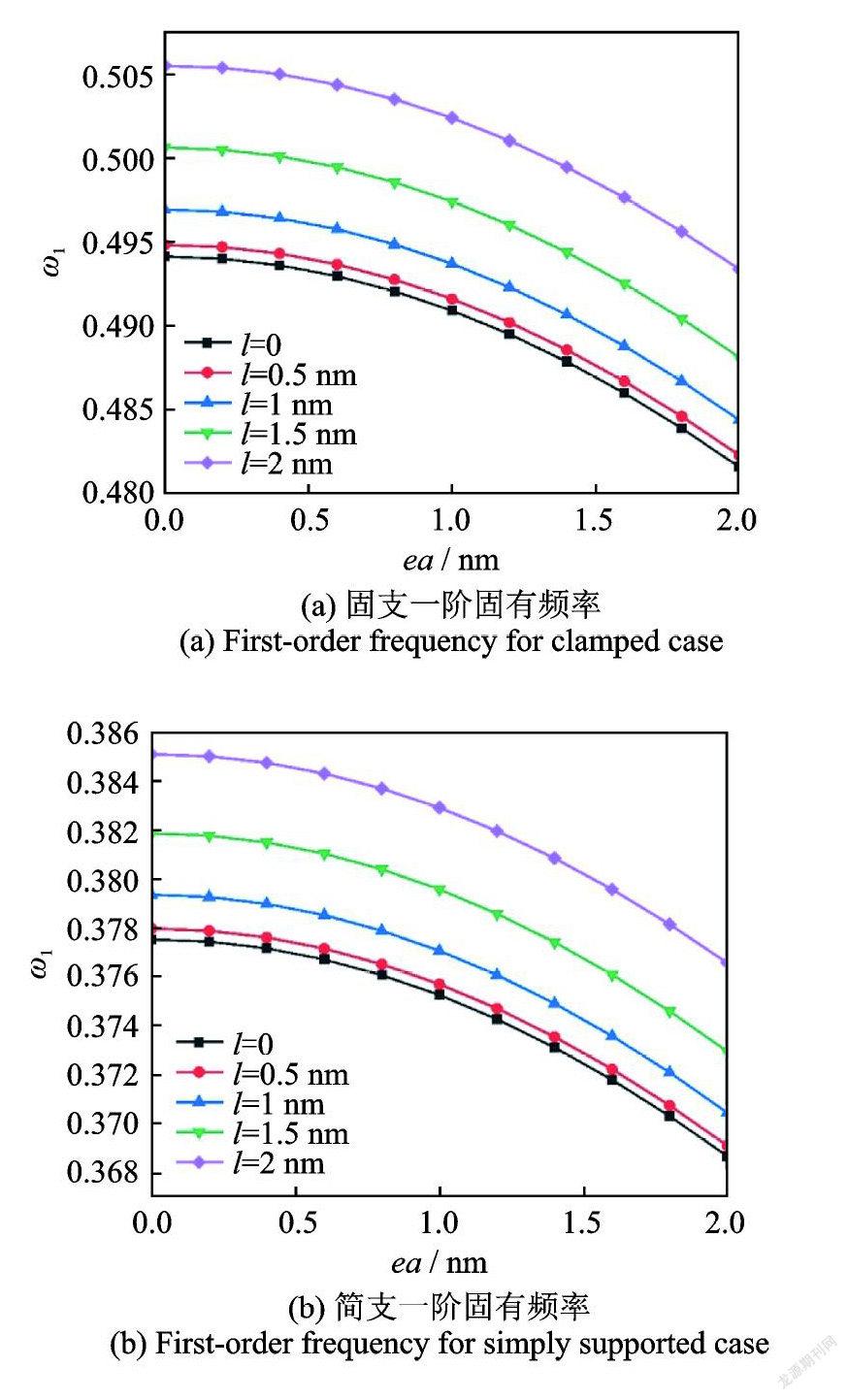
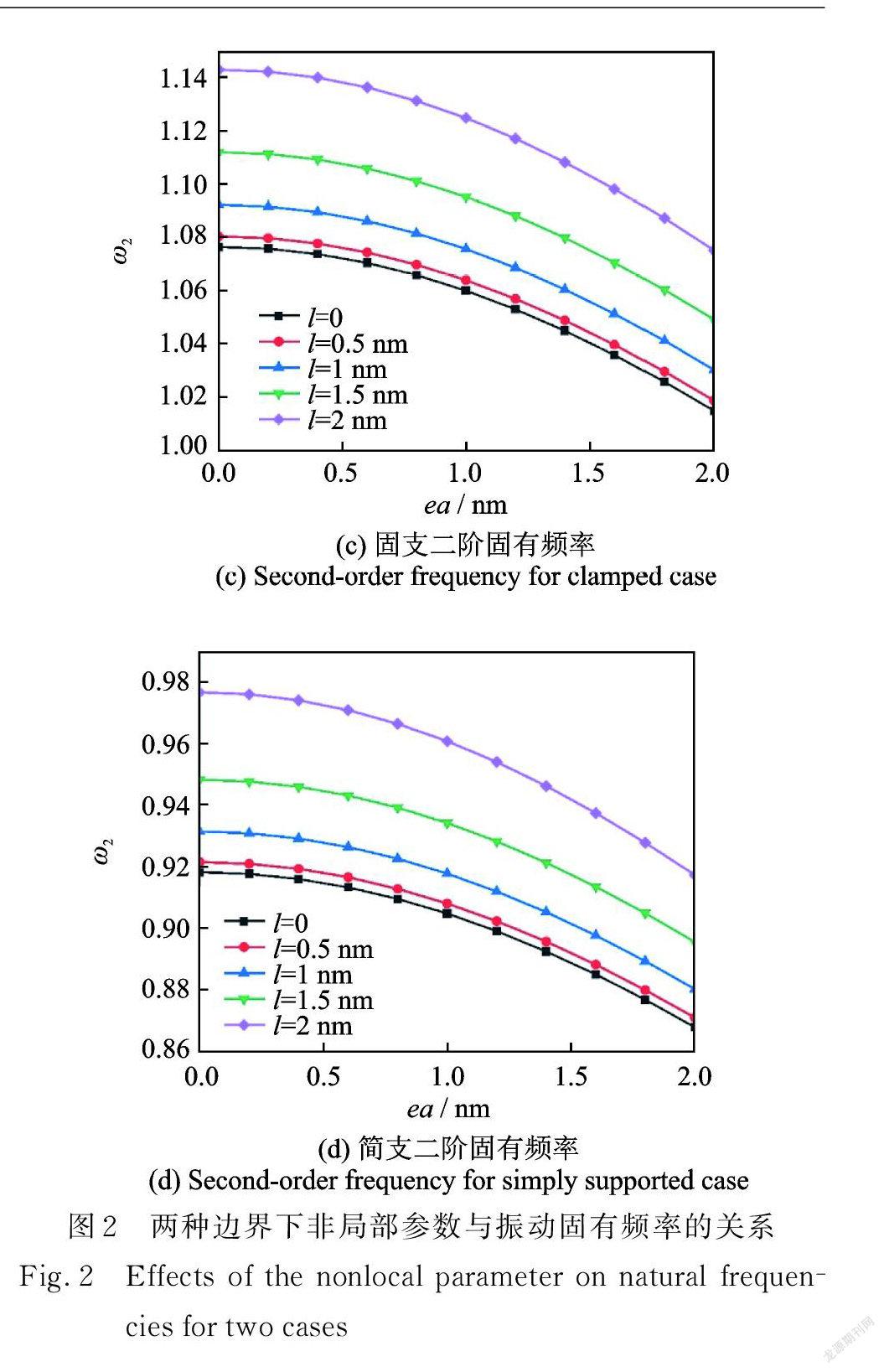
图2计算了应变梯度特征参数 l 分别取0，0.5，1，1.5和2 nm 时，非局部参数ea对固支和简支外边界下纳米圆板前两阶无量纲固有频率的影响。压电纳米圆板的振动固有频率随着非局部参数ea的增大而减小，固有频率的降低意味着纳米结构刚度的弱化，这表明非局部参数对纳米结构起到软化作用。

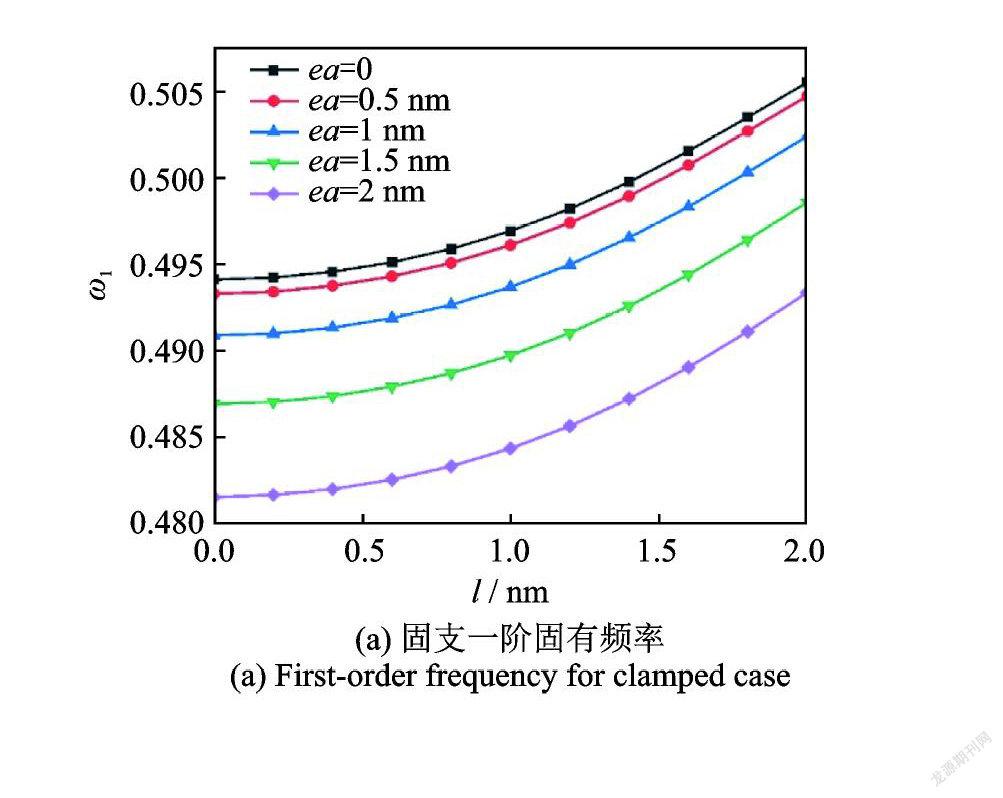
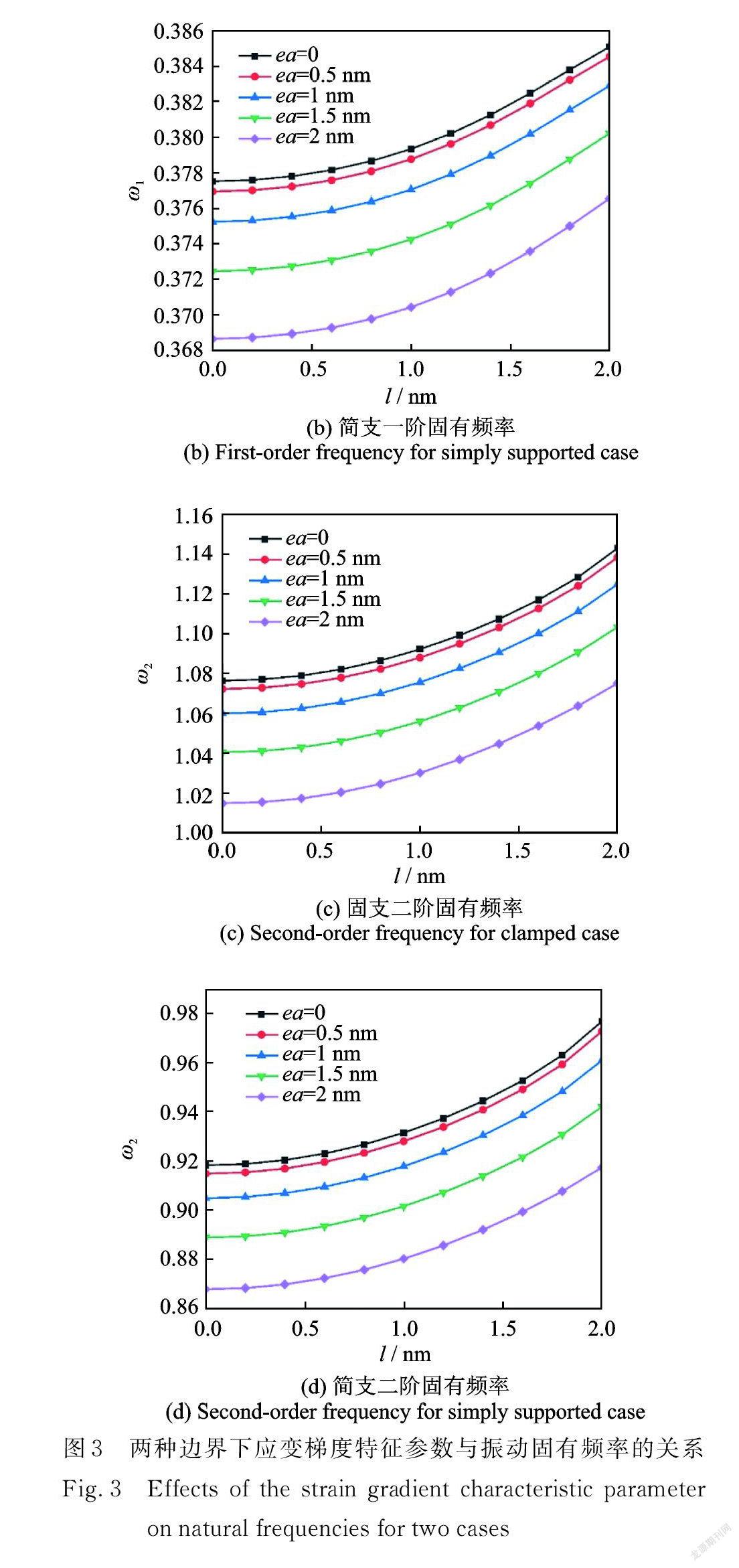
图3给出了非局部参数ea分别取0，0.5，1，1.5和2 nm 时，应变梯度特征参数 l 对纳米圆板前两阶固有频率的影响。可见振动固有频率随着应变梯度特征参数的增大而增大，因此应变梯度特征参数对纳米结构起到硬化作用。

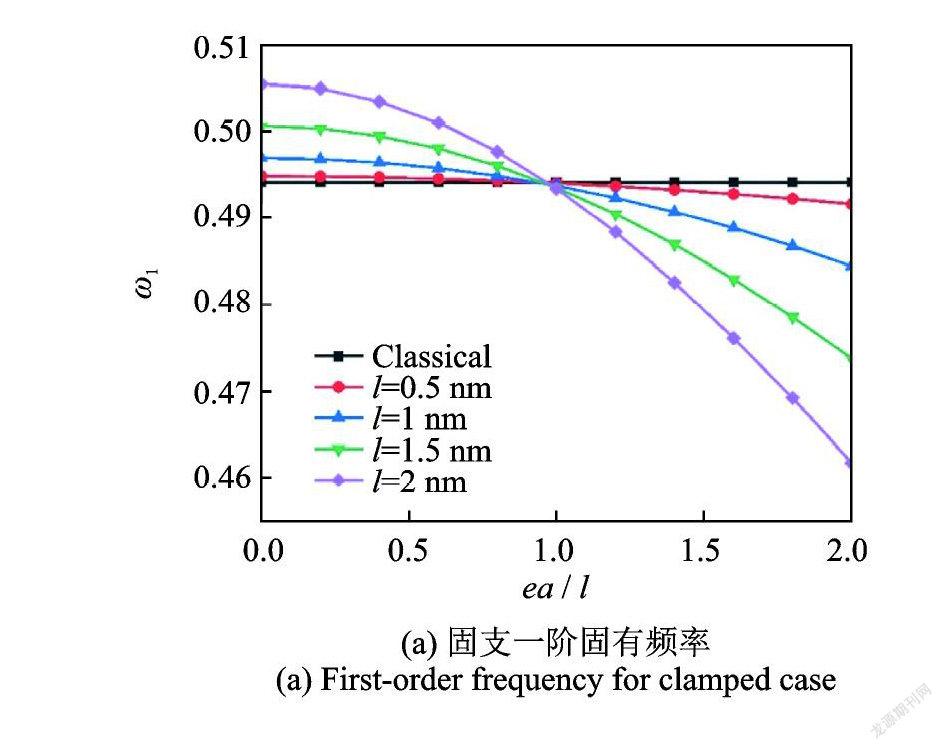
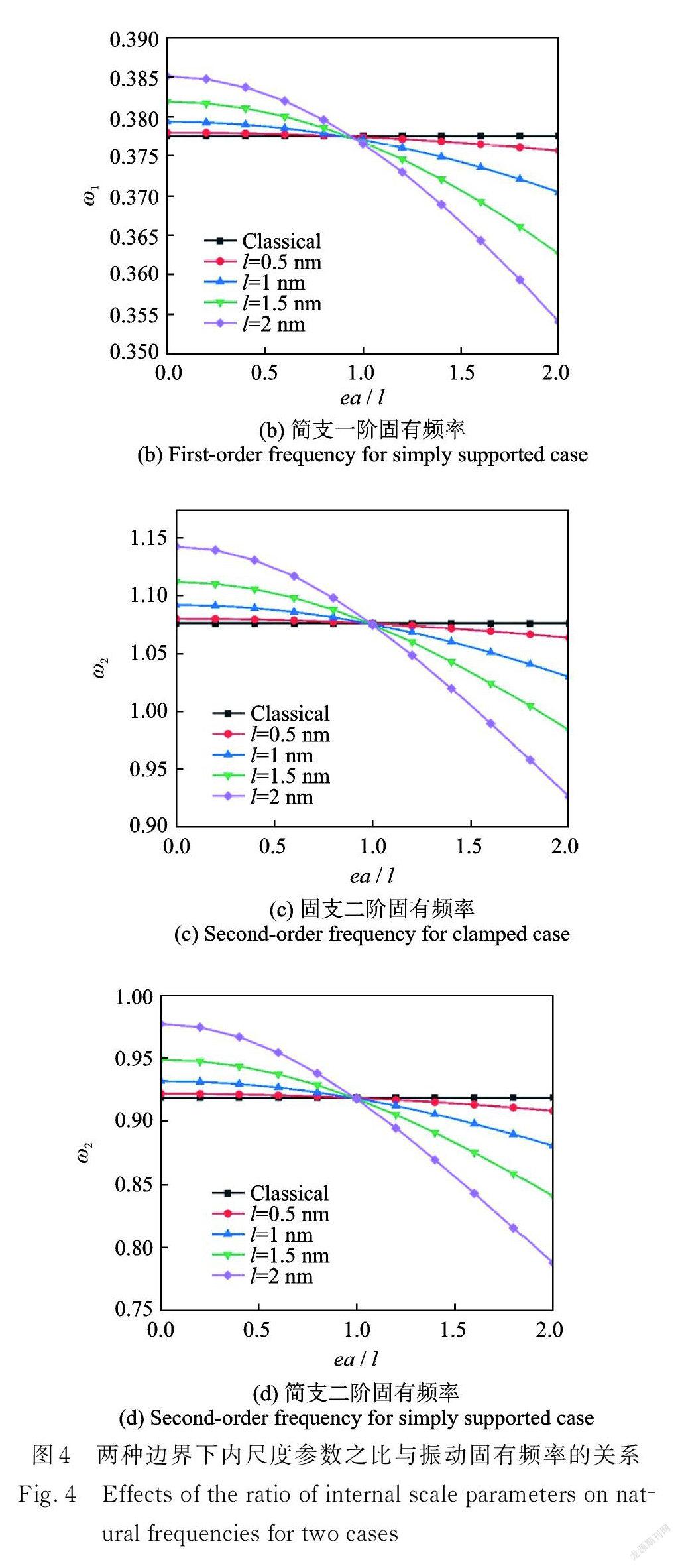
图4显示了固支和简支两种边界下，非局部参数与应变梯度特征参数的比值ea/l 对纳米圆板前两阶固有频率的影响。压电纳米圆板的固有频率随着ea/l 的增大而减小。从理论本构上显见，当ea=l=0时，结果将退化到经典连续介质模型结果。实际上，只要当ea=l，即使二者不为零，压电纳米圆板的固有频率都将不随ea/l 的改变而改变，且固有频率退化为经典连续介质理论结果，这表明两类内尺度参数对纳米结构的软/硬化作用相互抵消。这一特殊现象表明：两类内尺度参数对压电纳米圆板振动特性的影响存在内在关联。首先，非局部参数的存在削弱了纳米圆板的等效刚度，应变梯度特征参数则增强了纳米圆板的等效刚度，二者作用趋势相反，但作用强度恰好相同，因此在相反趋势中存在一个特殊点使得二者作用效果互相抵消。其次，非局部参数与应变梯度特征参数的量级相当，这就使得当二者大小相等时，一侧所引起的软化效果正好填补了另一侧的硬化效果，因此即使两类内尺度参数没有分别为零，非局部应变梯度理论结果仍然回归到经典连续介质理论结果。当ea<l 时，振动固有频率大于经典连续介质理论下的固有频率，此时内尺度参数对压电纳米圆板的刚度起到硬化作用；当ea>l 时，振动固有频率小于经典连续介质理论结果，此时内尺度参数对压电纳米圆板的刚度起到软化作用。因此，非局部参数与应变梯度特征参数这两类内尺度参数之间存在耦合关系，二者相比的数量关系将决定非局部应变梯度理论中内尺度效应的具体体现，亦即压电纳米圆板中的动力软化或硬化现象。

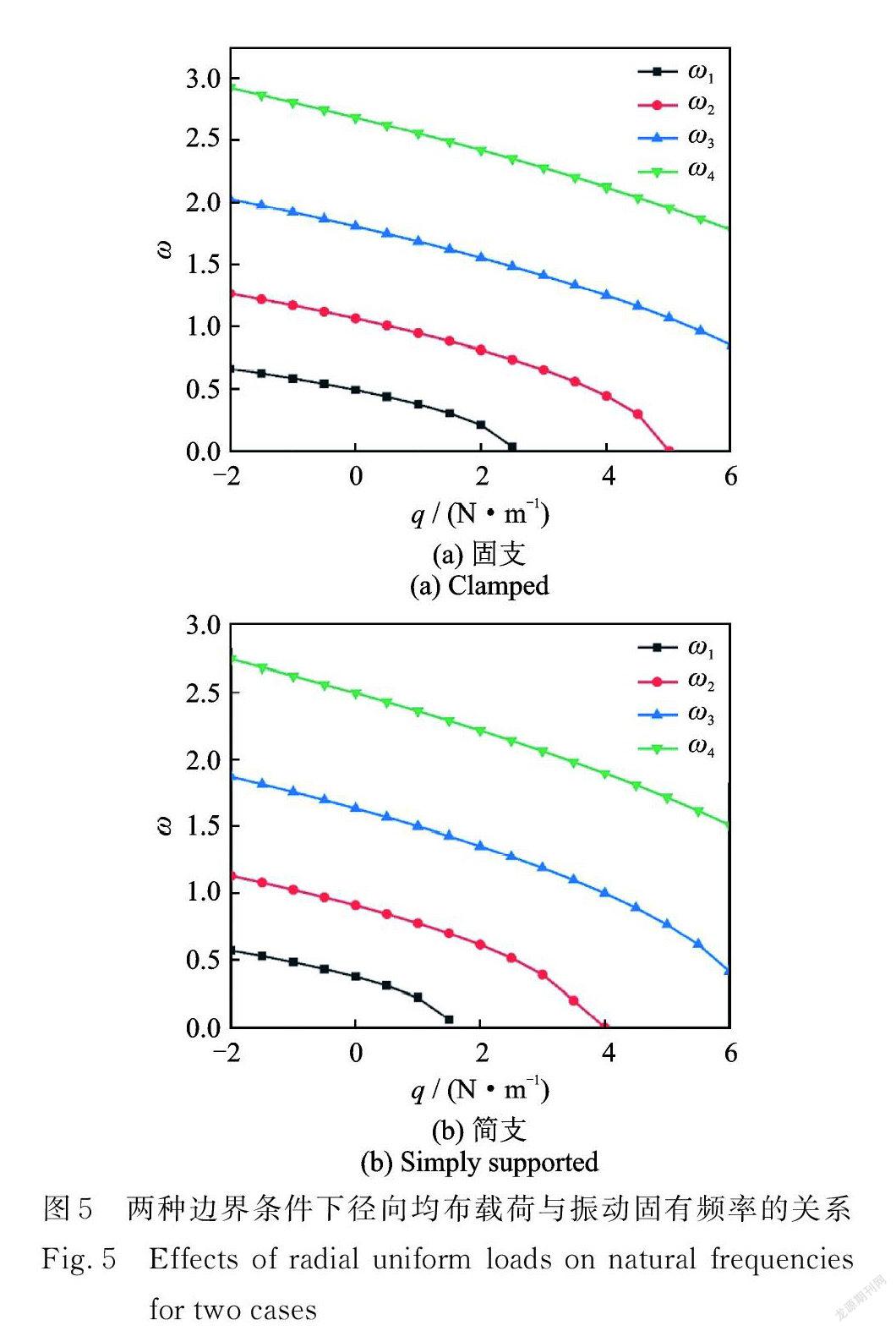
图5计算了 l=0.5 nm，ea=1 nm 时，径向均布载荷对压电纳米圆板前4阶无量纲振动固有频率的影响，可见固有频率随着径向压力的增大而减小，随着径向拉力的增大而增大。在径向压力从0增长到6 N/m 的过程中，第一阶和第二阶固有频率相继减小至零，压电纳米圆板的振动出现失稳，表明振动对径向外力的作用较为敏感。简支边界下压电纳米圆板在承受集度为1.541 N/m 的均布压力时开始失稳，而固支边界下在承受集度为2.518 N/m 的均布压力集度时开始失稳，表明简支外边界约束较固支外边界更易受外部压缩载荷干扰。

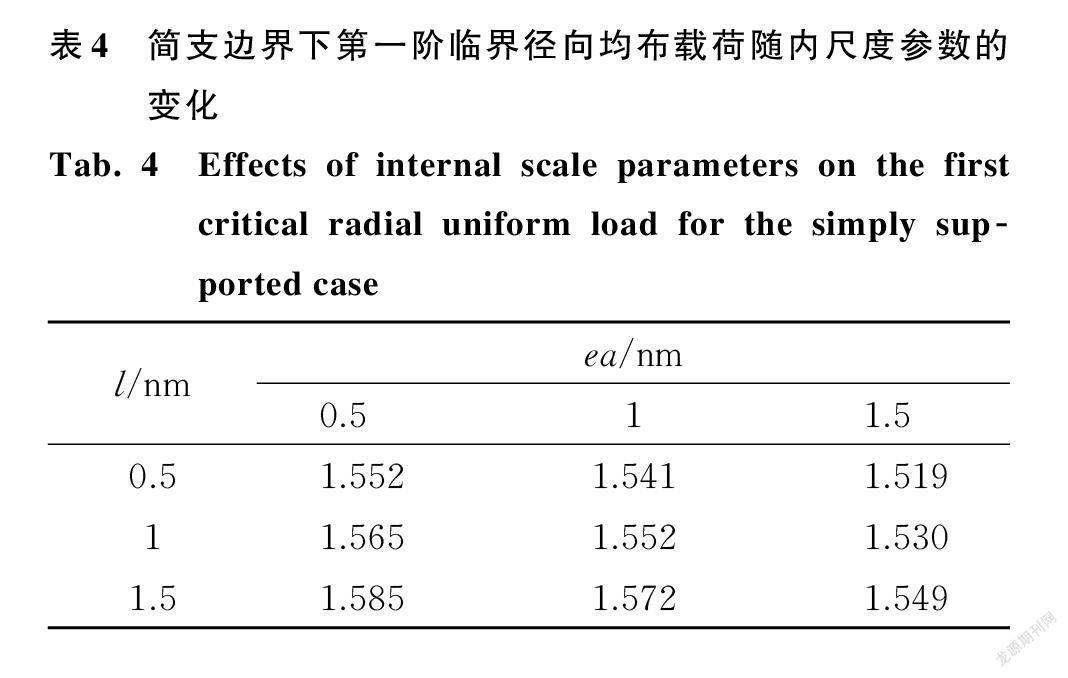
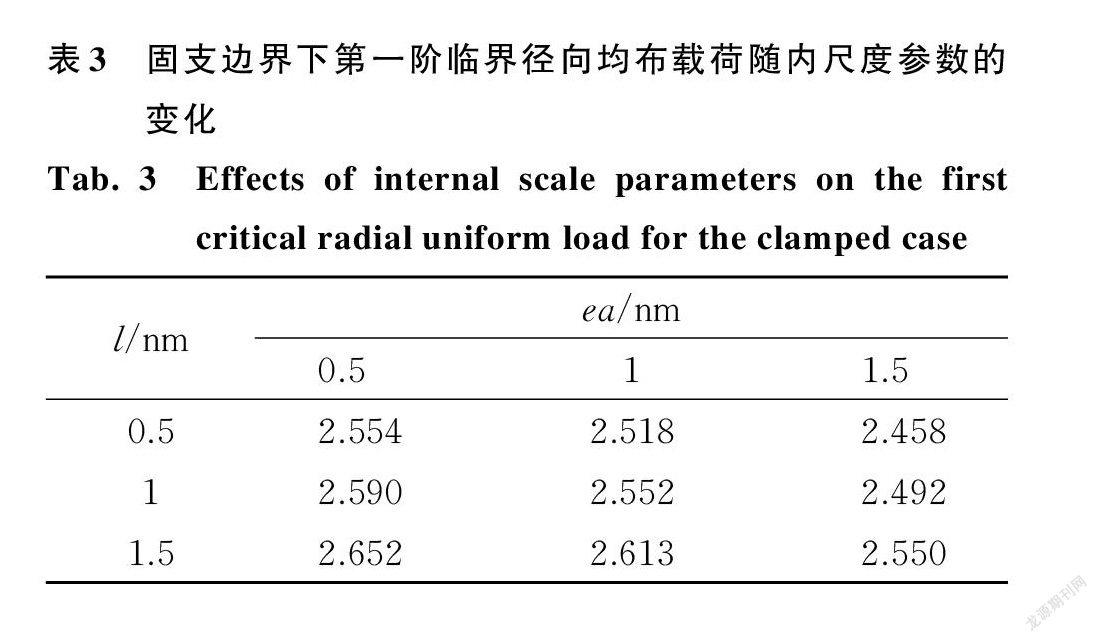
为进一步研究非局部参数与应变梯度特征参数对结构失稳时径向均布载荷临界值的影响，表3和表4分别计算了固支和简支边界下，第一阶临界径向均布载荷随内尺度参数的变化。由表中可以看出，临界径向均布载荷随非局部参数的增大而減小，随应变梯度特征参数的增大而增大。临界径向均布载荷越大代表结构刚度越大，这一现象再次验证前文结论。

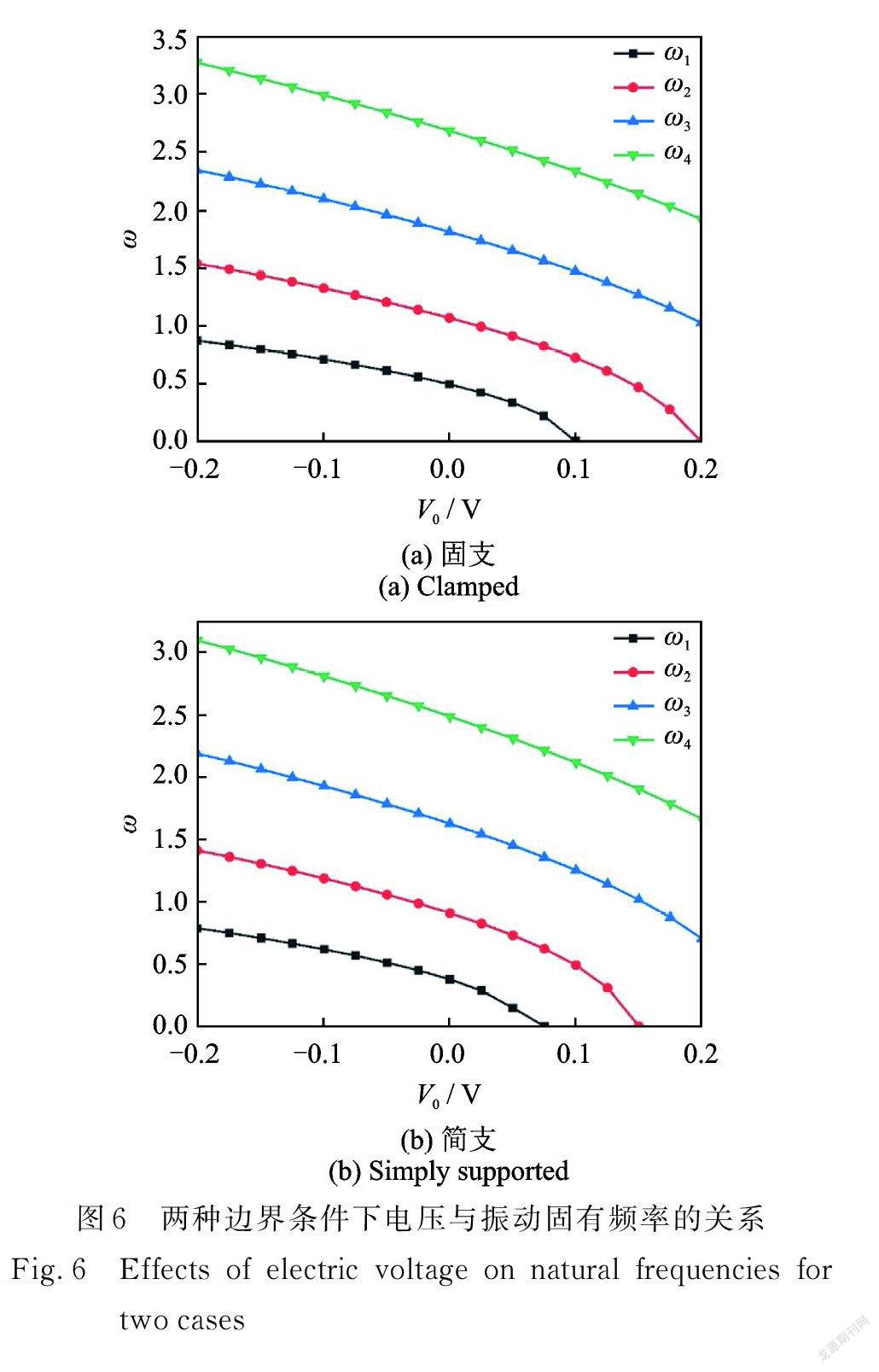
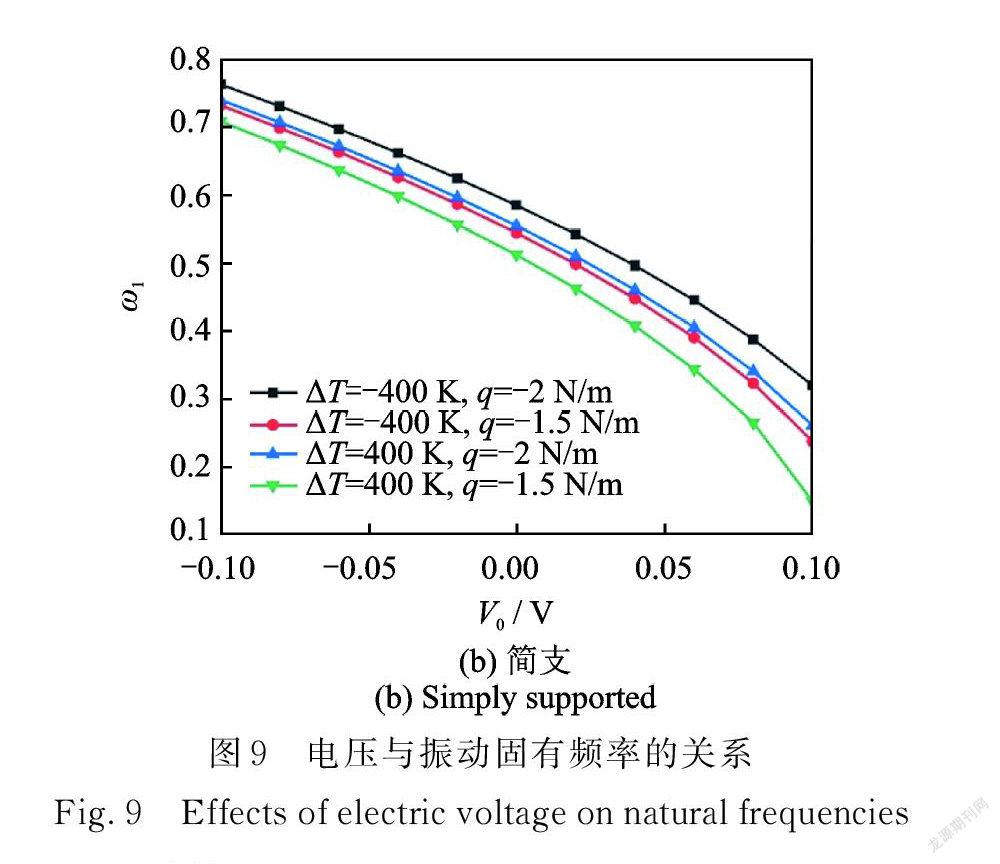
图6分别给出了 l=0.5 nm，ea=1 nm 时，固支和简支边界压电纳米圆板上下表面的外部电压 V0对前4阶无量纲振动固有频率的影响。压电纳米圆板的固有频率受外部电压的影响较大，电压从−0.2 V 增加到0.2 V 时，压电纳米圆板的固有频率出现明显的下降。这是因为当正电压作用在纳米圆板的上下表面时，圆板面内产生径向压缩效果，削弱圆板的刚度，导致固有频率随着正电压的增大而减小；当负电压作用在纳米圆板的上下表面时，圆板面内产生径向拉伸效果，导致固有频率随着负电压的增大而增大。这在物理上可解释如下：由电压引起的压力表达式 NE =-2 31 V0，可知当正电压加载在纳米圆板上下表面时，压电系数31可将 z 方向的电压转化为 r 方向的径向内力，且31为负值，所以 NE 为正值，即径向压缩效果；而当负电压加载在纳米圆板上下表面时，引起的压力 NE 为负值，即径向拉伸效果。

特别地，当电压增大到一定值时，第一阶和第二阶固有频率相继减小为零，系统出现失稳。简支边界下压电纳米圆板在电压取0.0591 V 时失稳，而固支边界下压电纳米圆板在电压取0.0965 V 时失稳，同样的外部静电压对简支压电纳米板的约束力乃至内力产生更大的影响，因此更容易发生失稳。

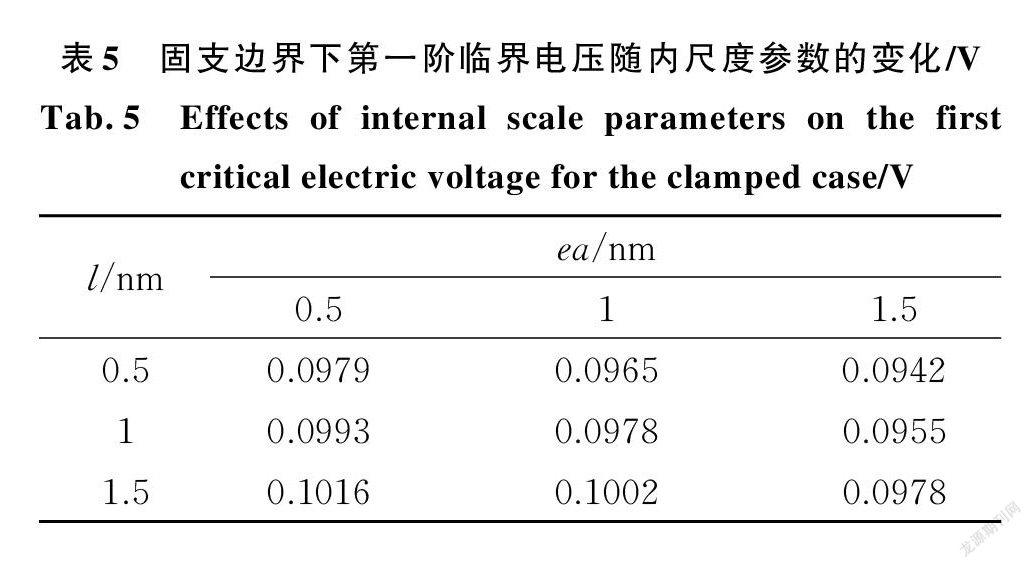
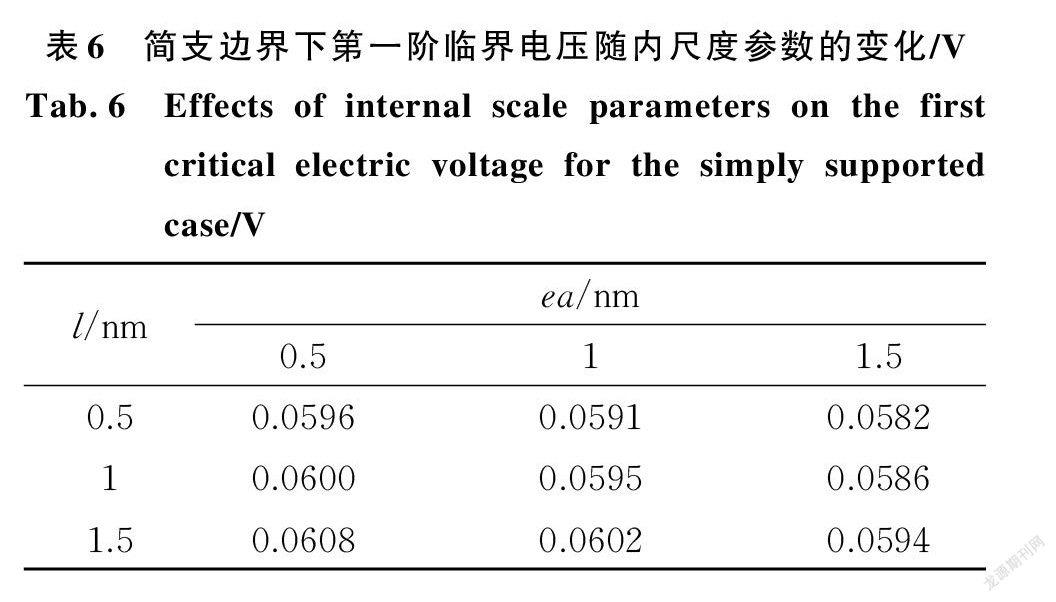
为进一步研究非局部参数与应变梯度特征参数对结构失稳时临界电压的影响，表5和表6分别计算了固支和简支边界下，第一阶临界电压随内尺度参数的变化。可见临界电压随非局部参数的增大而减小，随应变梯度特征参数的增大而增大。临界电压越大代表结构刚度越大，再次验证了前文结论。

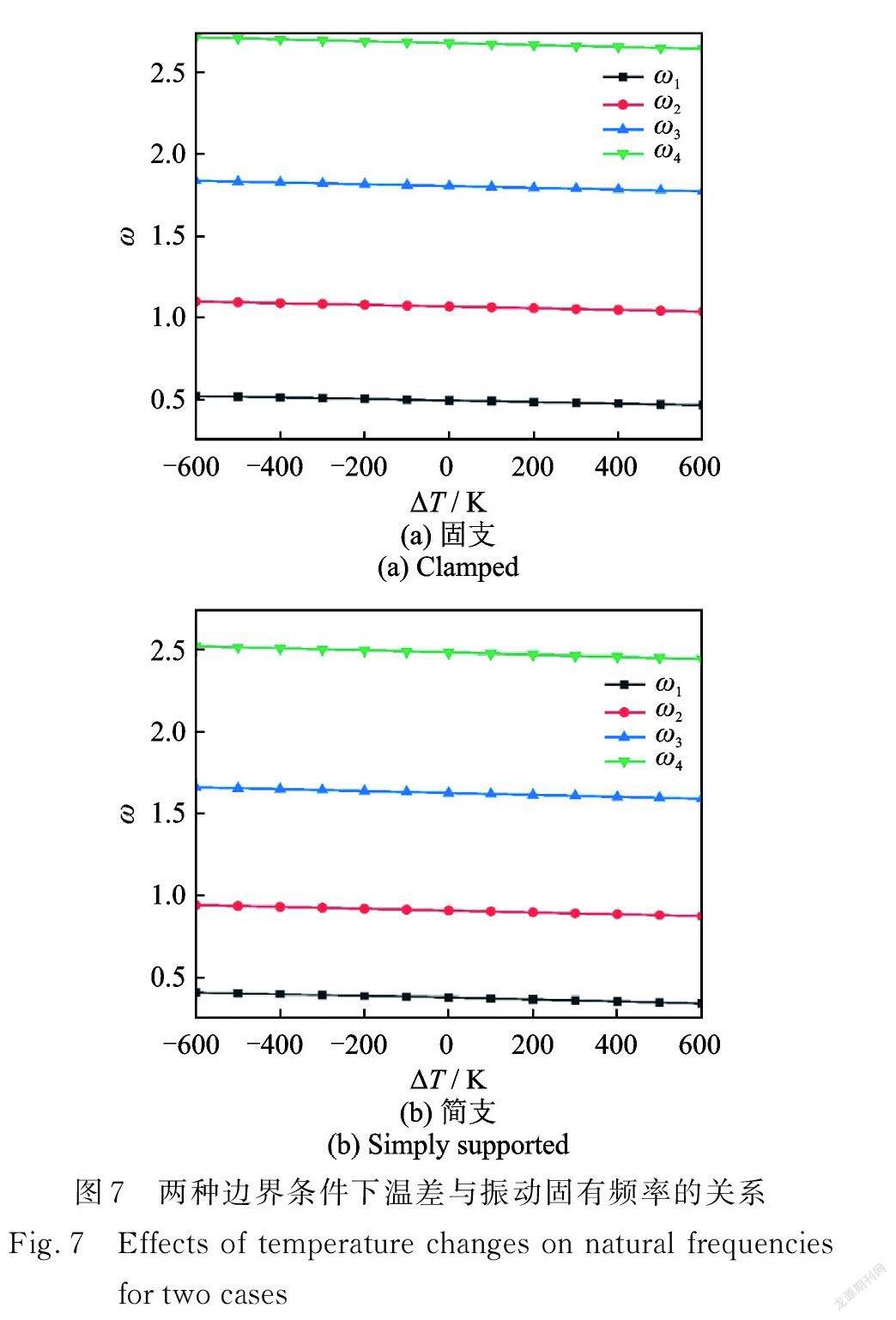
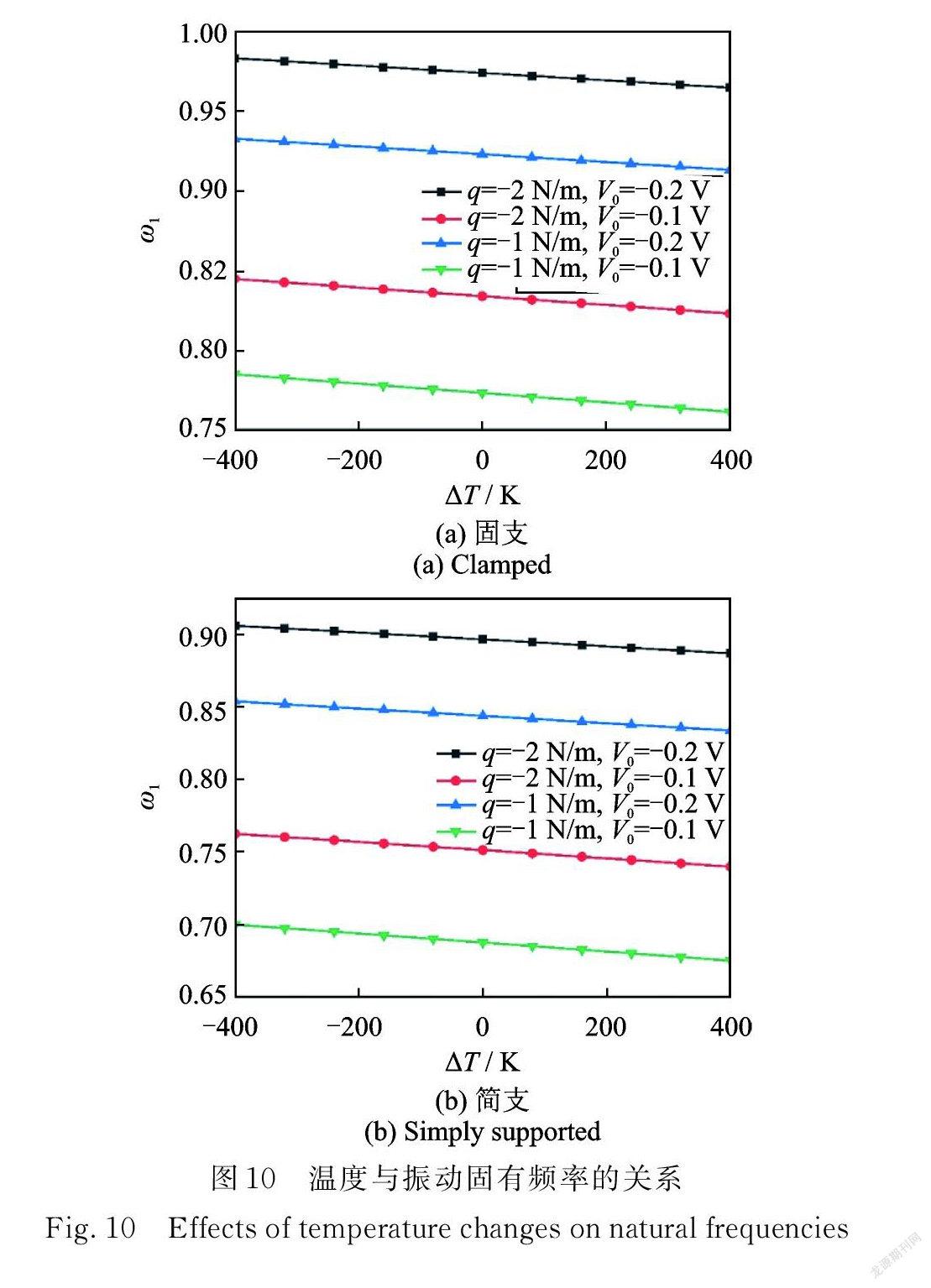
图7讨论了固支和简支两种边界下，l=0.5 nm 和ea=1 nm 时，温差ΔT 对压电纳米圆板前4阶固有频率的影响。压电纳米圆板的固有频率受温差影响相对较小，在温差由−600 K 升到600 K 时，固有频率小幅下降。这是由于温度升高会使材料膨胀从而产生径向压力，导致固有频率降低，但 PZT⁃4压电材料的热释电常数和热弹性模量较小，对温度不敏感，这使得压电纳米圆板的固有频率受温度变化影响也较小。

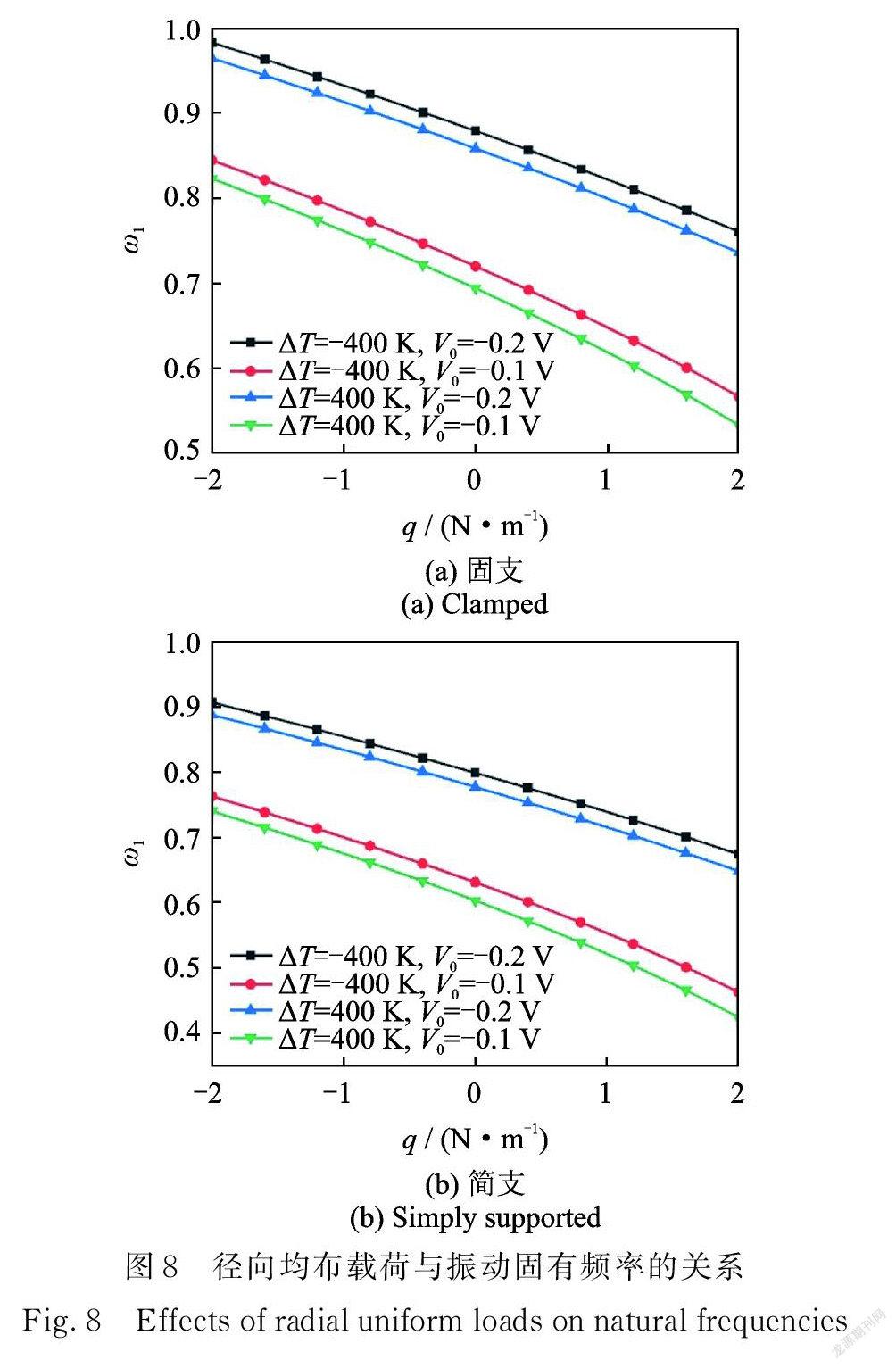
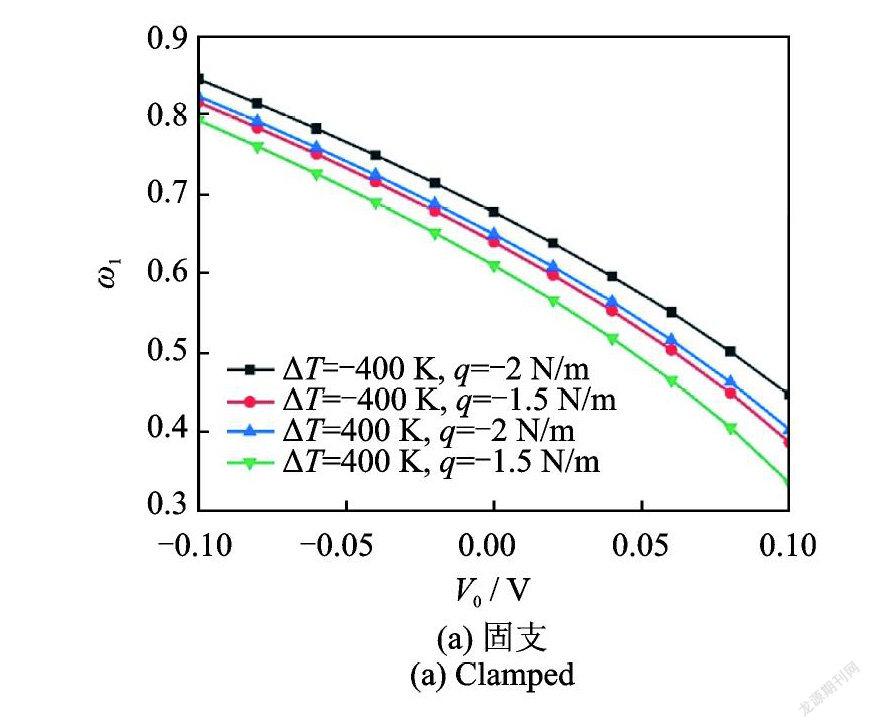
为了进一步揭示多场耦合情形下轴对称压电纳米圆板的振动特性，图8～10分别给出了压电纳米圆板一阶频率随径向均布载荷、电压以及温差的变化关系，其中体现了热⁃力⁃电多场参数的共同作用，并给定尺度参数 l=0.5 nm，ea=1 nm 。由图8（ a ）可知，当Δ T=-400 K ，V0=-0.2 V 时，q 从-2 N/m 变化到2 N/m 将引起一阶频率降低22.66%；当ΔT=-400 K，V0=-0.1 V 时，一阶频率降低了33.26%。这表明电压与径向载荷对振动固有频率的影响存在耦合效应，即负电压的减小助推了径向压力增大带来的纳米圆板刚度削弱的现象，且彼此耦合程度较大。当ΔT=400 K，V0=-0.2 V 时，q 从-2 N/m 变化到2 N/m 将引起一阶频率降低23.71%。这表明温度和径向载荷之间也存在耦合效应，但彼此耦合程度较低。由图8（b）可见固支边界条件下也有类似现象。同样地，根据图9和10，可以发现温度和电压之间也存在耦合效应，但耦合程度较低。此外，外物理场参数不影响内尺度参数对压电纳米圆板振动频率的作用机制。

4 结论

1）振动固有频率随非局部参数的增大而减小，随应变梯度特征参数的增大而增大。当非局部参数小于应变梯度特征参数时，压电纳米圆板表现出硬化特征；当非局部参数大于应变梯度特征参数时，表现出软化特征；当非局部参数等于应变梯度特征参数时，压电纳米圆板的刚度保持不变并等于相应的经典连续介质理论结果。非局部参数和应变梯度特征参数对压电纳米圆板的作用强度相当。

2）压电纳米圆板固有频率随径向压力和正电压的增大而减小，随径向拉力和负电压的增大而增大。在一定的径向载荷和电压作用下，纳米圆板的振动出现失稳现象。临界径向载荷与临界电压均随着非局部参数的增大而减小，随着应变梯度特征参数的增大而增大。

3）压电纳米圆板固有频率随温差的增大而略有减小，相比于外部力场和电场，压电纳米圆板振动对温度变化相对不敏感。简支外边界与固支外边界条件相比，压电纳米圆板的振动对前者相对更敏感。外物理场参数对压电纳米圆板振动特性的影响存在相互耦合，但不影响内尺度参数对压电纳米圆板振动频率的作用机制。

参考文献：

[1] 刘承斌，陈伟球，吕朝锋，等.内含弹性介质功能梯度压电球壳的径向振动调控[ J ].固体力学学报，2017，38（6）：537-543.

Liu  Chengbin，Chen Weiqiu，LüChaofeng，et al . Ex ⁃ act analysis and tuning of radial vibration of functionally graded piezoelectric spherical shells filled with an elastic medium[ J ]. Journal of Solid Mechanics，2017，38（6）：537-543.

[2]  田文祥，仲政.层状磁电复合材料界面共线裂纹平面问题分析[ J ].力学季刊，2018，39（2）：258-269.

Tian  Wenxiang，Zhong  Zheng . Analysis  for  the  plane problem of layered magnetoelectric composites with col⁃ linear  interfacial  cracks [ J ]. Quarterly  of  Mechanics，2018，39（2）：258-269.

[3] 沈纪苹，刘金建，李成，等.轴向运动压电纳米板的非局部热-力-电耦合振动[ J ].振动工程学报，2017，30（3）：378-388.

Shen Jiping，Liu Jinjian，Li Cheng，et al . Thermo-elec? tro-mechanical  vibration  of axially  moving piezoelectric nanoplates[ J ]. ，2017，30（3）：378-388.

[4] 王光庆，崔素娟，武海强，等.多稳态压电振动能量采集器的动力学模型及其特性分析[ J ].振动工程学报，2019，32（2）：252-263.

Wang Guangqing，Cui Sujuan，Wu Haiqiang，et al . Dy⁃ namical model and characteristics of a multi-stable piezo⁃ electric vibration energy harvester[ J ]. Journal of Vibra ⁃ tion Engineering，2019，32（2）：252-263.

[5]  Wang L F，Hu H Y . Flexural wave propagation in sin⁃gle-walled  carbon  nanotubes [ J ]. Physical  Review  B，2005，71（19）：195412.

[6]  Zhang Y Y，Shen H M，Wang Y X，et al . Combinedeffects of surface energy and couple stress on the nonlin⁃ ear bending of FG-CNTR nanobeams[ J ]. International

Journal of Modern Physics B，2020，34（11）：2050103.

[7]  Huang Z X . Coaxial stability of nano-bearings construct⁃ed by double-walled carbon nanotubes[ J ]. Nanotechnol⁃ ogy，2008，19（4）：045701.

[8]  Zhao  X ，Zhu  W  D ，Li  Y  H . Analytical  solutions  ofnonlocal  coupled  thermoelastic  forced  vibrations  of mi⁃ cro-/nano-beams  by  means  of  Green′s  functions [ J ]. Journal of Sound and Vibration，2020，481：115407.

[9]  Lim C W，Zhang G，Reddy J N . A higher-order nonlo⁃cal  elasticity  and  strain  gradient theory  and  its  applica⁃ tions in wave propagation[ J ]. Journal of the Mechanics and Physics of Solids，2015，78：298-313.

[10] Mehrez S，Karati S A，DolatAbadi P T，et al . Nonlo ⁃cal dynamic modeling of mass sensors consisting of gra⁃ phene  sheets  based  on  strain  gradient  theory [ J ]. Ad ⁃ vances in Nano Research，2020，9（4）：221-235.

[11] Wu Q N，Chen H H，Gao W . Nonlocal strain gradientforced  vibrations  of FG-GPLRC nanocomposite micro⁃ beams[ J ]. Engineering with Computers，2020，36（4）：1739-1750.

[12] Gholipour  A ，Ghayesh  M  H . A  couplednonlinearnonlocal  strain  gradient  theory  for  functionally  graded Timoshenko  nanobeams [ J ]. Microsystem  Technolo⁃ gies，2020，26（6）：2053-2066.

[13] Li H B，Wang X，Wang H L，et al . The nonlocal fre ⁃quency behavior of nanomechanical mass sensors based on the multi-directional vibrations of a buckled nanorib⁃ bon [ J ]. Applied  Mathematical  Modelling ，2020，77：1780-1796.

[14] Shen J P，Wang P Y，Li C，et al . New observations ontransversedynamics  ofmicrotubules based  on nonlocal strain gradient theory[ J ]. Composite Structures，2019，225：111036.

[15] Tang H S，Li L，Hu Y J，et al . Vibration of nonlocalstrain  gradient  beams  incorporating  Poisson′s  ratio  and thickness  effects [ J ]. Thin-Walled  Structures ， 2019，137：377-391.

[16] Zhang  P ，Qing  H . Exact  solutions  for  size-dependentbending of Timoshenko curved beams based on a modi? fied  nonlocal  strain  gradient  model[ J ]. Acta  Mechani⁃ ca，2020，231（12）：5251-5276.

[17] Chen W，Wang L，Dai H L . Nonlinear free vibration ofnanobeams based on nonlocal strain gradient theory with the consideration of thickness-dependent size  effect[ J ]. Journal  of  Mechanics  of  Materials  and  Structures，2019，14（1）：119-137.

[18] Li C，Qing H，Gao C F . Theoretical analysis for staticbending of Euler-Bernoulli using different nonlocal gradi⁃ ent  models [ J ]. Mechanics  of Advanced  Materials  and Structures，2021，28：1965-1977.

[19] Xu X J，Zheng M L . Analytical solutions for buckling ofsize-dependent Timoshenko beams[ J ]. Applied Mathe⁃ matics  and  Mechanics （English  Edition）， 2019，40（7）：953-976.

[20]王中林.压电式纳米发电机的原理和潜在应用[ J ].物理，2006，35（11）：897-903.

Wang Zhonglin . Piezoelectric nanogenerators-their prin⁃ciple  and  potential  applications[ J ]. Physics ，2006，35（11）：897-903.

[21] Motezaker  M ，Jamali  M ，Kolahchi  R . Application  ofdifferential  cubature  method  for  nonlocal  vibration， buckling and bending response of annular nanoplates in⁃ tegrated by piezoelectric  layers based  on  surface-higher order  nonlocal-piezoelasticity  theory [ J ]. Journal  ofComputational  and  Applied  Mathematics ，2020，369：112625.

[22] Eltaher M A，Omar F A，Abdalla W S，et al . Mechani⁃cal analysis of cutout piezoelectric nonlocal nanobeam in⁃ cluding  surface  energy  effects[ J ]. Structural  Engineer⁃ ing and Mechanics，2020，76（1）：141-151.

[23] Karimiasl  M ，Kargarfard  K ，Ebrahimi  F . Buckling  ofmagneto-electro-hygro-thermal  piezoelectric  nanoplates system  embedded  in  a  visco-Pasternak  medium  based on  nonlocal  theory [ J ]. Microsystem  Technologies，2020，26（2）：673-673.

[24] Arefi M，Pourjamshidian M，Arani A  G . Dynamic in⁃stabilityregion  analysis of sandwich piezoelectric nano- beam  with  FG-CNTRCs  face-sheets  based  on  various high-order  shear deformation  and nonlocal  strain  gradi⁃ ent theory[ J ]. Steel and  Composite  Structures ，2019，32（2）：157-171.

[25] Masoumi A，Amiri A，Talebitooti R . Flexoelectric ef⁃fects  on  wave  propagation  responses  of  piezoelectric nanobeams  via  nonlocal  strain  gradient  higher  order beam  model[ J ]. Materials Research Express ，2019，6（10）：1050d5.

[26] Yang Y，Zou J Q，Lee K Y，et al . Bending of circularnanoplates with consideration of surface effects[ J ]. Mec ⁃ canica，2018，53（4-5）：985-999.

[27] Mahinzare M，Alipour M J，Sadatsakkak S A，et al . Anonlocal strain gradient theory for dynamic modeling of a rotary thermo piezo electrically actuated nano FG cir⁃ cularplate[ J ]. Mechanical Systems and Signal Process⁃ ing，2019，115：323-337.

[28] Wang Q . On buckling of column structures with a pairof  piezoelectric  layers [ J ]. Engineering  Structures，2002，24（2）：199-205.

[29] Wang  Q ，Wang  C  M . The  constitutive  relation  andsmall scale parameter of nonlocal continuum mechanics for  modelling  carbon  nanotubes [ J ]. Nanotechnology，2007，18（7）：075702.

[30] Li C，Lai S K，Yang X . On the nano-structural depen⁃dence of nonlocal dynamics and its relationship to the up⁃ per limit of nonlocal scale parameter[ J ]. Applied Mathe⁃ matical Modelling，2019，69（5）：127-141.

[31] Liew K M，Han J B，Xiao Z M . Vibration analysis ofcircularMindlin  plates  using  the differential  quadrature method[ J ]. Journal of Sound and Vibration，1997，205（5）：617-630.

Thermal-mechanical-electrical coupling vibration of axisymmetricpiezoelectric circular nanoplates accounting fornonlocal strain gradient effects

LUO Qiu-yang1，LI Cheng1，2

（1.Department of Vehicle Engineering，School of Rail Transportation，Soochow University，Suzhou 215131，China；2.School of Automotive Engineering，Changzhou Institute of Technology，Changzhou 213032，China）

Abstract： The coupling vibration performances of axisymmetric piezoelectric circular nanoplates under thermo-electro-mechanical fields are studied based on the nonlocal strain gradient theory and Mindlin plate theory . Hamilton’s principle is used to develop the equations of motion in the framework of nonlocal strain gradient constitutive relations，and the differential quadrature method is ad⁃ opted to solve differential equations describing the theoretical model . The influences of internal scale parameters and external field parameters on natural frequencies of piezoelectric circular nanoplates are analyzed . It shows that the natural frequency of piezoelec⁃ tric circular nanoplate decreases with an increase of the nonlocal parameter，and increases with an increase of the strain gradient characteristic parameter . When the nonlocal parameter is less than the strain gradient characteristic parameter，the circular nano⁃ plate demonstrates a hardening behavior . When the nonlocal parameter is greater than the strain gradient characteristic parameter， it demonstrates a softening behavior . When the nonlocal parameter is equal to the strain gradient characteristic parameter，the stiff⁃ ness degenerates into the corresponding result of classical continuum theory . Additionally，it indicates that the natural frequencies decrease with an increase of the radial compressive load and positive voltage，and increase with an increase of the radial tensile load and negative voltage . The natural frequency decreases slightly with an increase of the temperature . In particular，it is found that while increasing the radial load and voltage to a certain value，the vibration instability occurs . The effects of the nonlocal parameter and strain gradient characteristic parameter on the critical radial load and critical voltage are analyzed accordingly .

Key words ： coupling vibration；piezoelectric circular nanoplate；nonlocal strain gradient；Mindlin plate theory；axisymmetric

作者簡介：罗秋阳（1996—），男，硕士研究生。电话：17761906520；E-mail：qyluo@stu .suda .edu .cn。

通讯作者：李成（1983—），男，教授。电话：18020272969；E-mail：licheng@suda .edu .cn。