考虑气象和地理因素的电网传输特性计算及灵敏度分析
贾学勇,董晓明,孙宏文,王亚松,陈 凡
(电网智能化调度与控制教育部重点实验室(山东大学),山东省济南市 250061)
0 引言
电力系统运行状态不仅取决于电网的电气参量,同时也受风速、气温、海拔等环境因素的影响,特定的电网运行特征指标通常与关键气象要素密切相关。近年来,多起造成严重后果的电网事故都与极端气象条件的影响密不可分[1-3]。受全球变暖的影响,极冷和极热天气频繁发生,如2014 年美国纽约出现118 年来最低温,2018 年1 月美国东海岸的爆发性气旋影响打破了近百年来的最低气温纪录,2018 年3 月极端初寒流横扫欧洲,2019 年2 月哈萨克斯坦最低气温跌破-40 ℃,2020 年美国西部大部分地区遭遇极端高温天气,位于洛杉矶市中心以北的伯班克市当日最高气温达到46.1 ℃,更靠近内陆沙漠的棕榈泉市气温高达50 ℃。类似的极端天气往往造成区域电网源-网-荷态势紧张,增加严重停电事故[4-5]发生的概率。据此,气象因素越来越受到电力系统分析和决策者的重视。
近年来,国内外对考虑气象因素的电力系统运行相关方向做了大量研究。对于单个输电线路的电气特性,IEEE 728 标准给出的环境因素对架空输电导体运行温度影响的分析报告[6]为众多研究提供了重要的理论依据。以此为基础,文献[7-8]考虑输电线路电阻随运行温度的变化,从电压稳定层面计算线路传输功率极限,对线路实际运行具有重要的指导意义。文献[9-12]中提出的动态热定值技术对受环境影响的输电导体实时温度进行跟踪和评估,并根据导体材料能够耐受的最大允许运行温度决定导体的载流量。文献[13-15]则根据输电线路的动态热定值实时增大风电接入容量,评估结果表明环境协同的电力系统具有更高的风电接纳度。考虑电热耦合的整个电网潮流状态的分析计算方法主要分为统一迭代求解方法[16-19]和交替迭代求解方法[20]。交替迭代求解方法具有计算速度快、占用内存少等优点,但收敛性没有很好的保障;统一迭代求解方法具有严格的数学推导,牛顿迭代具有二阶收敛特性和统一完整的灵敏度矩阵即雅可比矩阵结构,能为VQ灵敏度分析、连续潮流计算[21-22]等提供必要的模型和算法支撑。文献[16-18]将导体温度作为状态变量引入潮流计算中,提出了电热耦合潮流计算方法。文献[19-20]考虑气象因素对线路参数进行了修正,能够获得更加准确的潮流结果。文献[21-22]提出了用于计算功率传输裕度的电热耦合连续潮流模型。上述研究虽然都涉及了电热耦合理论,但对环境因素的变化及其对功率流影响的研究尚显不足。
综上,气象因素对输电线路及电力系统的运行具有显著的影响,但目前能够显现气象和地理因素差异的电网功率传输特性的精细化建模与分析方法较少。对此,文献[20]的研究具有突破性意义,但所提电热协调与潮流计算交替迭代的方法难以适用于基于潮流模型的V-Q灵敏度分析等拓展分析方法。据此,本文将输电线路周围气象和地理信息以变量形式引入潮流模型,建立了考虑环境因素的统一迭代潮流模型及其求解算法。然后,依据所提算法,分析了不同环境因素的差异对电网功率传输特性的影响。最后,基于包含环境信息的拓展雅可比矩阵提出了计及环境因素的V-Q灵敏度分析方法,为准确分析计算潮流分布及评估电网运行状态提供更为精确的算法支撑。
1 理论分析与模型构建
1.1 计及环境因素的架空输电线路电热耦合分析
假设线路处于电热平衡状态,线路散发和产生的热量相等,线路温度最终将趋近于某一恒定值。当环境条件(比如风速、海拔高度以及环境温度等)改变或存在差异时,导线热平衡点将会改变,导体温度和电阻将过渡至新的平衡点。在电力系统需求变化缓慢的假设条件下,依据文献[6]中的静态热平衡方程可得:
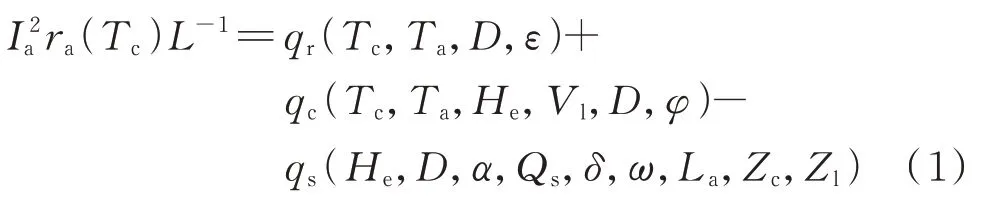
式中:Ia为线路载流量;ra为线路实际串联电阻;L为线路的长度;Tc为导体温度,本文假设导体温度均匀分布;Ta为导体周围环境温度;He为海拔高度;Vl为线路周围风速;D为导体直径;ε为辐射率;φ为风向角;α为导体对光照的吸收率;Qs为太阳光照强度;δ为太阳赤纬角;ω为时角;La为 地理纬度;Zc和Zl分别为太阳和导线的方位角;qr为线路因表面辐射散热;qc为线路因空气对流散热;qs为线路因太阳辐射吸收的热量。各参数的详细描述参考IEEE 738标准。
1)对流散热
导体对流散热分为自然对流散热qcn和强制对流散热qcf两种方式,则对流散热为:
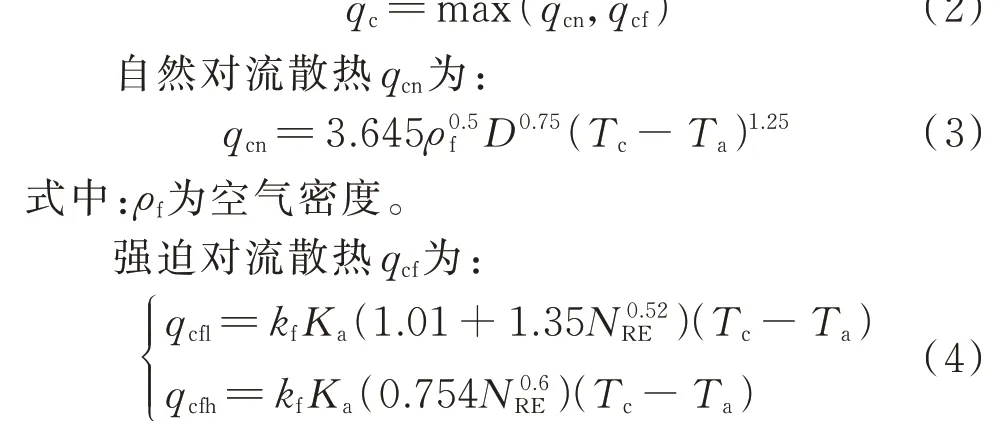
式中:qcfl为低风速时的强迫对流散热;qcfh为高风速时的强迫对流散热;kf为空气导热率;Ka为风向因子;NRE为雷诺数。qcf取qcfl和qcfh的最大值。
NRE可表示为风速函数,即

式中:Tf=(Tc+Ta)/2。
2)日照吸热
单位长度导体所吸收的太阳热量为:

式中:Ks为太阳高度校正因子;θs为有效的太阳入射角。
3)辐射散热
辐射散热与导线直径及导体表面材料特性有关。
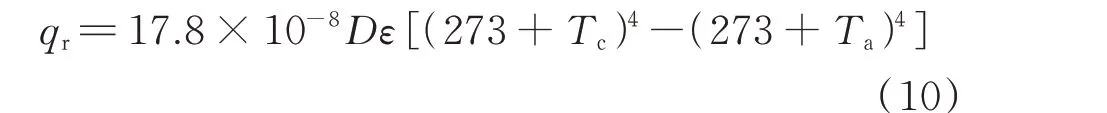
在传统电力系统的分析中,电阻常被视为常数,忽略其变化。实际上线路电阻与温度密切相关,在规定范围内线路温度与电阻呈近似线性关系,ra可以近似地表示为Tc的线性函数:
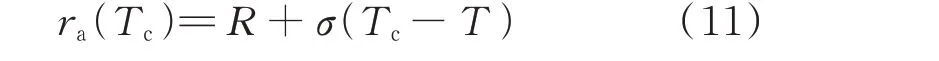
式中:σ为电阻温度系数;R为额定环境温度T下的单位长度导体的电阻。
推导式(1),可得第l条架空输电线路电流标幺值如式(12)所示。
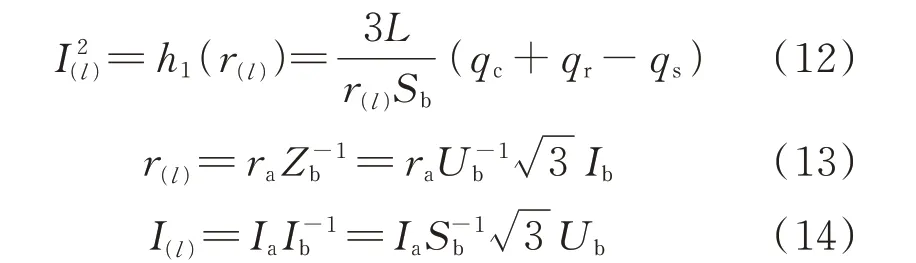
式中:r(l)和I(l)分别为ra和Ia的标幺值;h1(·)为表示r(l)和I2(l)关系的函数;Sb、Zb、Ib、Ub分别为功率、阻抗、电流、电压的基准值。
1.2 考虑环境因素的电热耦合统一潮流计算模型
本文将气象和地理因素引入传统潮流计算中,建立考虑环境因素的电热耦合统一潮流计算模型。假设电网架空线路均为星形连接,相电流等于线电流,表示为:
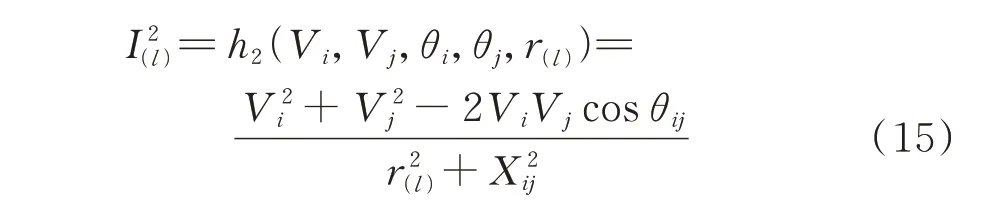
式中:Vi和Vj分别为节点i和节点j的电压幅值;θi和θj分别为节点i和节点j的电压相角;h2(·)为表示Vi、Vj、θi、θj、r(l)和I2(l)关系的函数;Xij为节点i至节点j的电抗;θij=θi-θj为节点i和j的电压相角差。
将式(12)和式(15)相减得到式(16)所示线路电热耦合方程h(l)(v,θ,r),其包含各环境参变量,显现其影响。
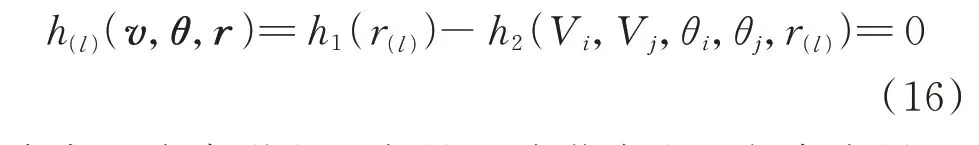
式中:r为串联电阻向量;v为节点电压相角向量;θ为节点电压相角向量。
将线路电热耦合方程和节点功率平衡方程联立,得到考虑环境因素的电热耦合统一潮流模型函数S(z):
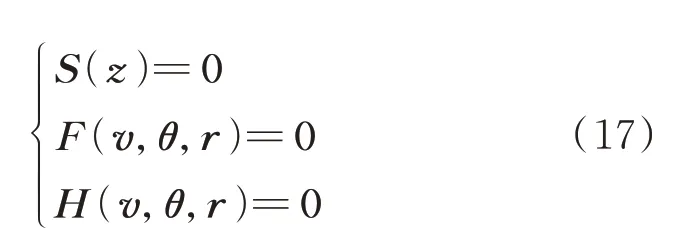
式中:F(v,θ,r)=[f1,f2,…,f2n-2]为功率平衡方程,其 中n为 网 络 的 节 点 数 目;H(v,θ,r)=[h(1),h(2),…,h(m)]为各输电线路电热耦合方程,其中m为架空输电线路的数目。下文将其简化为F和H。
求解式(17)的牛顿迭代关系如下:
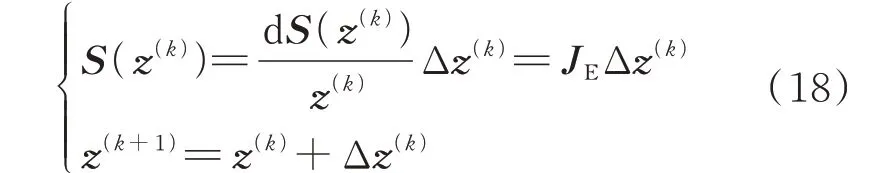
式中:z(k)为第k次迭代时的潮流状态量向量;Δz(k)为第k次迭代时的修正量向量,当Δz(k)元素绝对值最大值小于预先给定的精度参数εS时,迭代结束;JE为扩展雅可比矩阵,具体描述如式(19)所示。
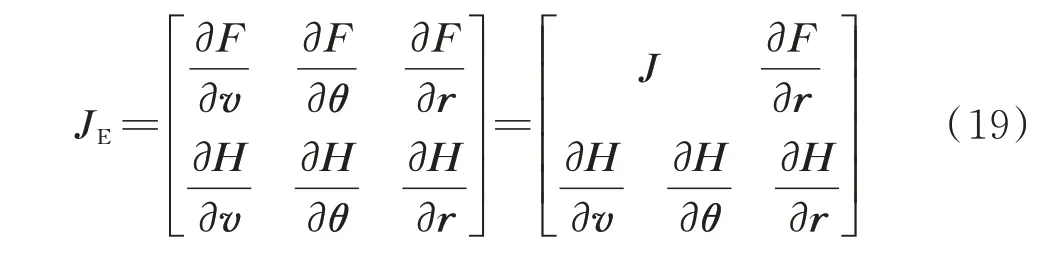
式中:J为传统的雅可比矩阵。
其中,F对r的偏导数的计算公式为:
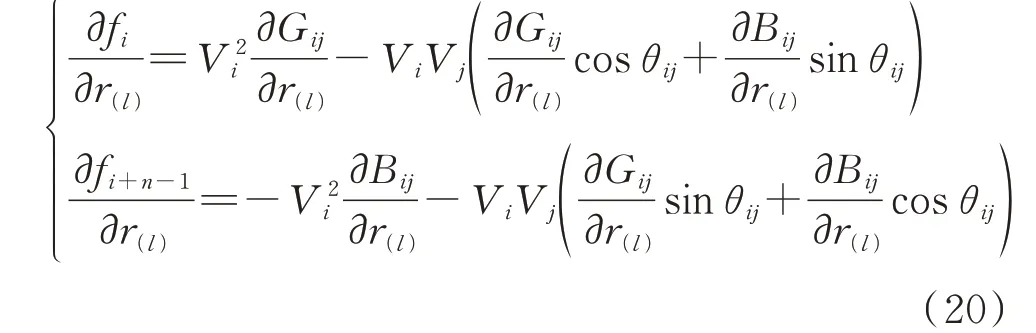
式中:Gij和Bij分别为节点i至节点j的电导和电纳,
其对r(l)的求导公式如式(21)所示。
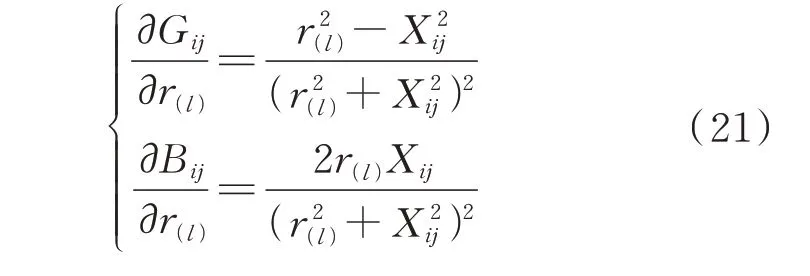
根据式(22)可计算式(19)中H对v的偏导数,其矩阵元素仅与线路l的首末节点电压幅值相关。
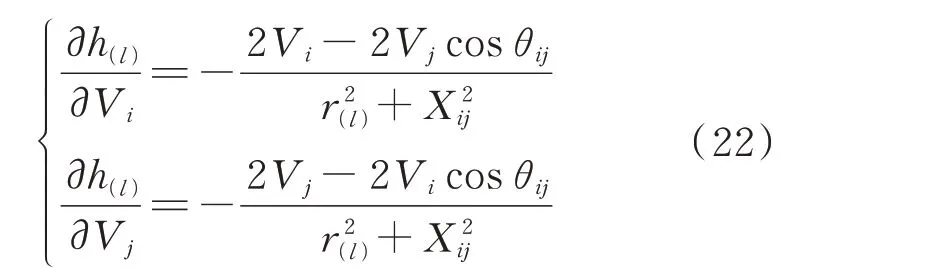
根据式(23)可计算式(19)中H对θ的偏导数,其矩阵元素仅与线路l的首末节点电压相角相关。

此时,参数L、Tc、Ta、T、D、ε、Vl、φ、He、α、Qs、δ、ω、La、Zc、Zl、σ取第l条线路的数据。
1)qr对r(l)的导数计算公式如下:


5)因qs与温度没有关系,其对r(l)求导为0。
考虑环境因素的电热耦合统一潮流计算流程如图1 所示。
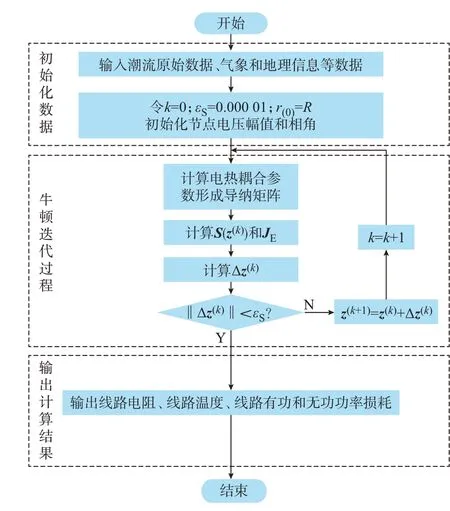
图1 考虑环境因素的电热耦合统一潮流计算流程Fig.1 Calculation process of electric and thermal coupling unified power flow considering environmental factors
2 环境参数对电网功率传输特性的影响
为了分析不同环境参数变化对电网功率传输特性的影响,通过考虑环境因素的电热耦合统一潮流计算方法和常规潮流方法计算的功率传输特性(电阻、有功和无功功率损耗)的差值占常规潮流计算方法计算的功率传输特性的百分比来计算传输功率特性的相差。本文选用IEEE 14 节点测试系统,设置节点2 有功功率为100 MW,节点3 有功功率为50 MW,节点6 有功功率为50 MW,其他数据与标准算例一致。电网线路环境参数基准值如表1所示,以干净环境下的参数计算太阳光照强度。
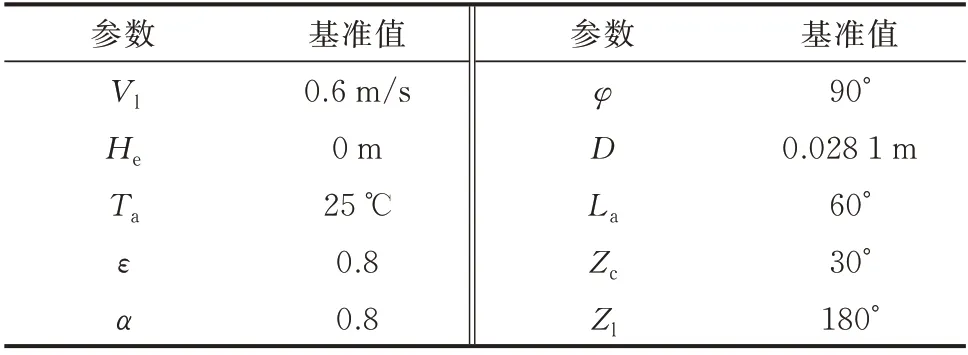
表1 电网线路环境参数基准值Table 1 Reference value of environmental parameters of power lines
2.1 风速变化对电网功率传输特性的影响
风速是对流散热的主要影响因素之一。假设该值变化范围为0~18 m/s,其他参数与基准值保持一致,得到风速与电网不同功率传输特性的关系曲线,如图2 所示。
由于线路5-6、4-7 和4-9 为变压器线路,不涉及环境因素,为此本文只研究非变压器线路。以常规潮流计算的电阻、有功和无功损耗为基准值。通过观察图2 可得,随着风速提高,线路电阻、有功和无功损耗与基准值差距不断缩小,线路温度不断降低,电网功率传输特性呈非线性变化。线路6-13 的电阻和温度降低幅度最大,风速为0时,电阻与其基准值相比约提高了19.08%,温度高达74.5 ℃。线路7-8的有功和无功损耗降低幅度最大,有功损耗为0.000 07 p.u.,无功损耗为0.000 23 p.u.;风速为0 时,线路7-8 有功损耗为0.000 1 p.u.,无功损耗为0.000 32 p.u.,与基准值相比约提高了42.86%和39.13%。
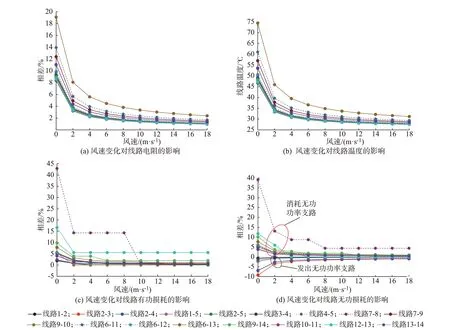
图2 风速变化对电网功率传输特性的影响Fig.2 Influence of wind speed change on power transmission characteristics of power grids
2.2 海拔高度变化对电网功率传输特性的影响
海拔高度对日照吸热和对流散热均有影响,设该值变化范围为0~4 000 m,其他参数与基准值保持一致,得到海拔高度与电网不同功率传输特性的关系曲线,如图3 所示。随着海拔高度的升高,线路电阻、有功和无功损耗与基准值差距不断增大,线路温度不断升高,功率传输特性基本呈线性变化。其中,线路6-13 的电阻和温度提升幅度最大,海拔高度为4 000 m 时,与基准值相比较,电阻约提高了17.91%,温度约高达71.43 ℃。线路7-8 的有功和无功损耗降低幅度最大,海拔高度为4 000 m 时,线路6-13 的有功和无功损耗提升幅度最大,有功损耗为0.000 1 p.u.,无功损耗为0.000 31 p.u.,有功和无功损耗与基准值相比约提高了42.86%和34.78%。
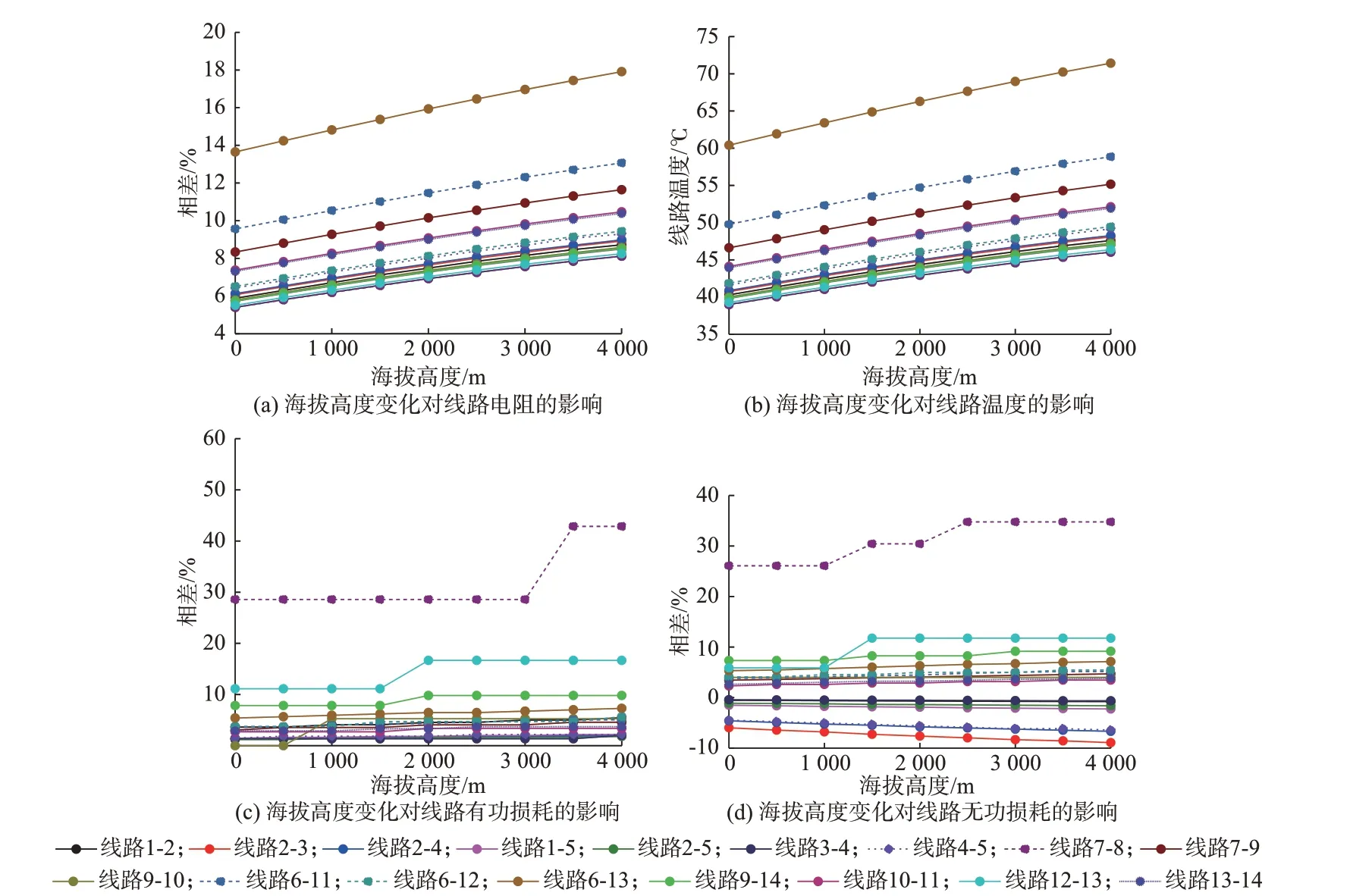
图3 海拔高度变化对电网功率传输特性的影响Fig.3 Influence of altitude change on power transmission characteristics of power grids
2.3 环境温度变化对电网功率传输特性的影响
环境温度是对流散热和辐射散热的主要影响因素之一,设该值变化范围为-40~50 ℃,其他参数与基准值保持一致,得到环境温度与电网不同功率传输特性的关系曲线,如图4 所示。
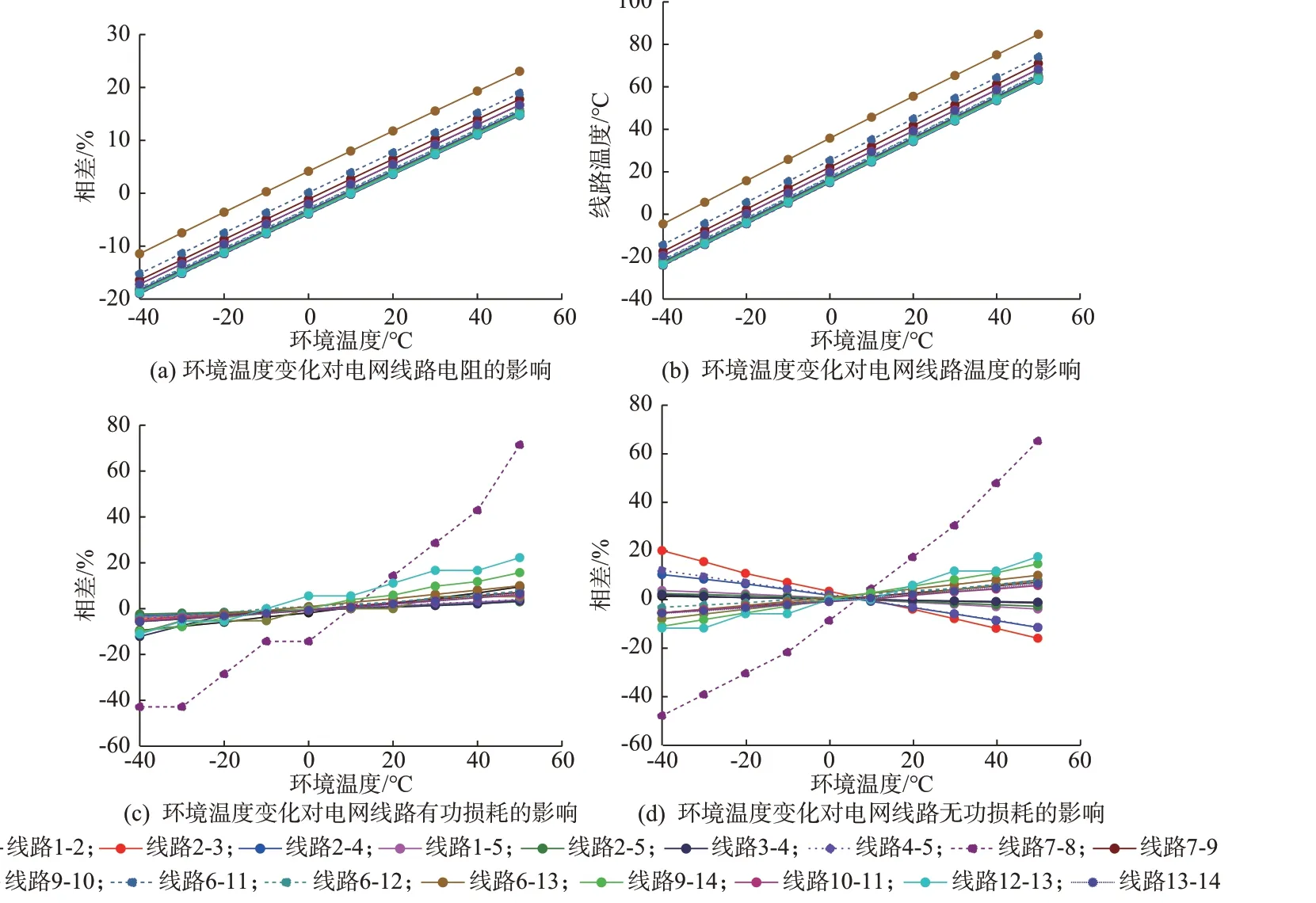
图4 环境温度变化对电网功率传输特性的影响Fig.4 Influence of environment temperature change on power transmission characteristics of power grids
图4 中,随着环境温度的升高,线路电阻、有功和无功损耗与基准值差距先缩小后增大(环境温度为0 ℃至10 ℃之间为电网功率传输特性变化的交接点),线路温度不断升高,功率传输特性基本呈线性变化。线路6-13 的电阻和温度变化幅度最大,环境温度为50 ℃时,电阻与其基准值相比约提高了23%,温度约高达84.7 ℃。线路7-8 的有功和无功损耗降低幅度最大,环境温度为50 ℃时,线路7-8 的有功和无功损耗提升幅度最大,有功损耗为0.000 12 p.u.,无功损耗为0.000 38 p.u.,与基准值相比约提高了71.43%和65.22%。
2.4 气象要素时空关联的电网传输特性分析
比较风速、海拔高度以及环境温度对功率传输特性的影响程度,可得环境温度影响电网传输特性的气象要素。由于邻近地理位置的温度之间存在空间相关性,温度逐日变化间存在时间相关性。本文选取了2020 年新疆维吾尔自治区14 个位置365 天的日平均温度,其数据曲线见附录A 图A1。
为分析不同位置之间日平均温度的相关性,采用Pearson 相关系数衡量不同位置日平均温度的相关性大小,计算公式为:
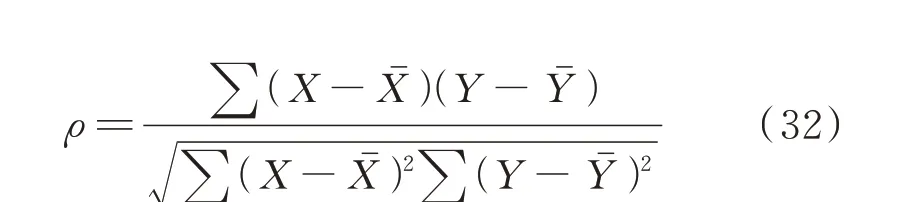
式中:X和Y表示不同位置365 天的日平均温度数据;Xˉ和Yˉ分别为X、Y的均值;ρ为X、Y的Pearson相关系数。式(32)计算得到的相关系数的绝对值越大,相关性越强。相关系数越接近1,正相关度越强;相关系数越接近-1,负相关度越强;相关系数越接近0,相关度越弱。通过对14×365 个日平均温度数据进行相关性分析计算,得到的新疆维吾尔自治区14 个位置之间日均温度相关系数见附录A 图A2。
依据收集数据和分析结果得出,夏季不同位置的日平均温度都较高,最高可达38 ℃;冬季不同位置的日平均温度都较低,最低可达-20 ℃。不同位置之间日平均温度对应的相关系数均在0.9 以上,这说明不同位置日平均温度之间具有高度相关性。当电网线路处于较高或较低的环境温度情况下,都会对导线温度和电阻产生影响,如忽略气象要素时空关联对电网功率传输特性的影响,这将会使得计算结果存在误差。为此,本文依托新疆维吾尔自治区2020 年14 个位置夏季和冬季两个典型日的气象数据和地理信息进行电网潮流计算,对比分析常规潮流模型与改进潮流模型的计算结果。
附录A 图A3 和图A4 展示了常规工况下以及夏季和冬季典型日电网不同节点的电压幅值和相角,并比较了考虑气象要素时空关联与常规潮流计算结果的相差。附录B 表B1 展示了常规工况下电网功率传输特性计算结果,不同季节电网功率传输特性的变化及差异如表2 所示。
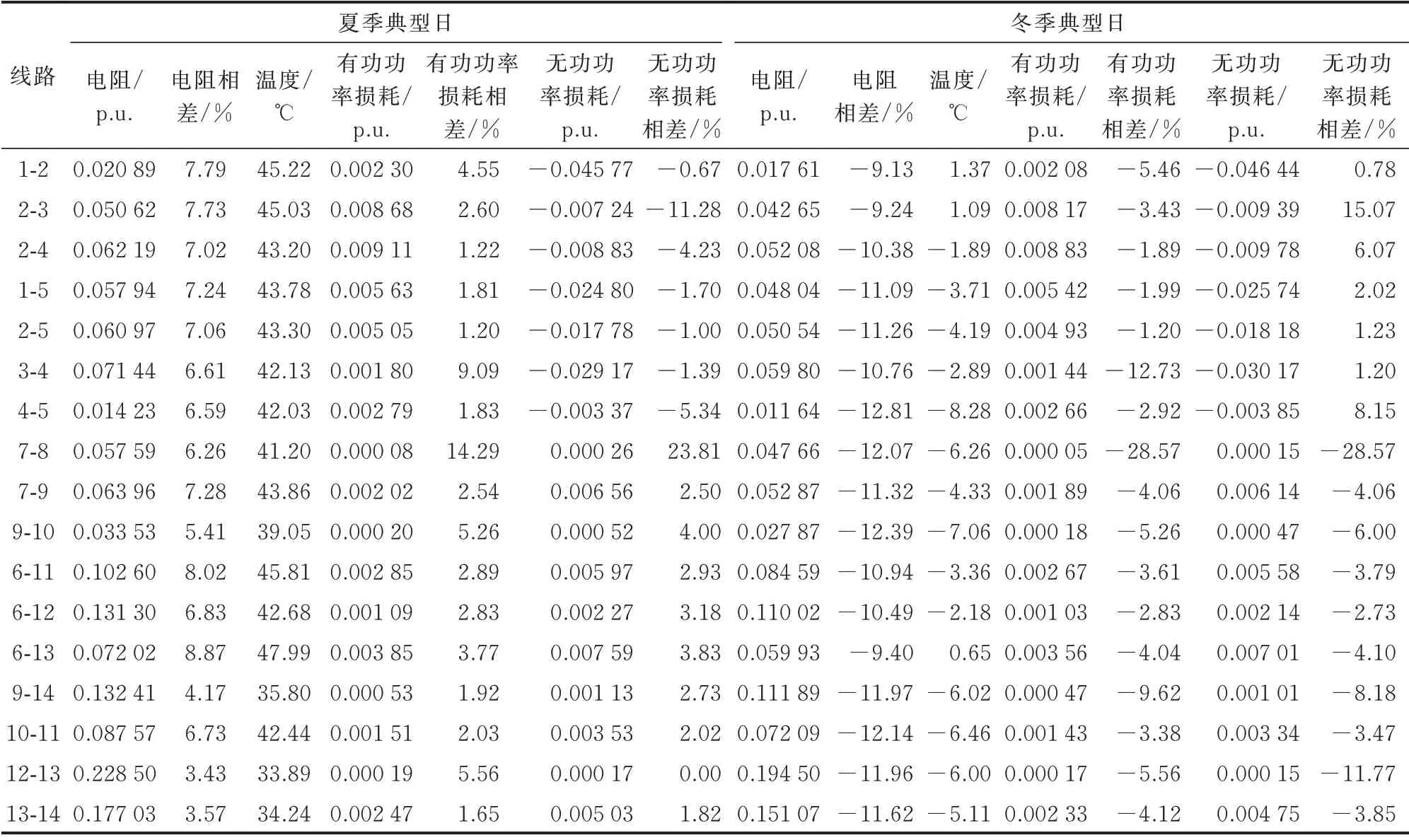
表2 不同季节电网功率传输特性的变化及差异Table 2 Variations and differences of power transmission characteristics of power grids in different seasons
由表2可得,采用夏季和冬季典型日气象数据,电网功率传输特性计算结果与常规方法计算结果相比有较大差距。夏季典型日中线路6-13电阻相差最大,可达8.87%,温度高达47.99 ℃,线路7-8 功率损耗相差最大,有功损耗相差可达14.29%,无功损耗相差可达23.81%;冬季典型日中线路4-5 电阻相差最大,可达-12.81%,温度低至-8.28 ℃,线路7-8 功率损耗相差最大,有功和无功损耗相差均达到了-28.57%。通过计算分析可得不同季节电网功率传输特性会有较大变化和差异,这表明了考虑气象时空关联对电网传输特性计算分析的必要性。
3 计及环境因素的V-Q 灵敏度分析
对于以牛顿法为基础的潮流计算,作为算法核心的雅可比矩阵是非线性功率平衡方程在潮流解附近的最优线性逼近,亦可以理解为状态量与控制量之间的灵敏度矩阵,能够为节点电压和注入无功功率(V-Q)之间的灵敏度分析提供支持。据此本文以常规雅可比矩阵与本文模型中的拓展雅可比矩阵进行V-Q灵敏度对比分析。
3.1 算法理论
在稳态情况下,电力系统中功率、电压之间关系的线性化方程可表示为:
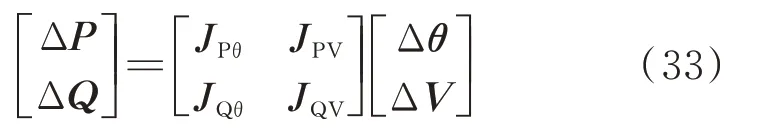
式中:ΔP为节点有功功率的增量;ΔQ为节点无功功率的增量;Δθ为节点电压相角的增量;ΔV为节点电压幅值的增量;JPθ、JPV、JQθ、JQV分别为雅可比矩阵J的子阵。雅可比矩阵各元素给出了功率与节点电压之间的灵敏度。
对于所有动态元件,当dΔx/dt=0 时(其中Δx为系统动态特性的状态变化量,t为时间),其功率和电压之间的线性关系为:
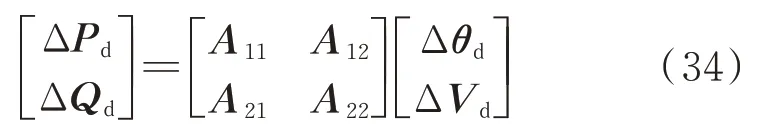
式中:ΔPd为动态元件输出的有功功率增量;ΔQd为动态元件输出的无功功率增量;Δθd为动态元件电压相角增量;ΔVd为动态元件电压幅值增量;A11、A12、A21、A22为式(33)中涉及动态元件元素的修正矩阵。
在每个运行点,保持有功功率为常数,令式(33)中ΔP=0,可得:
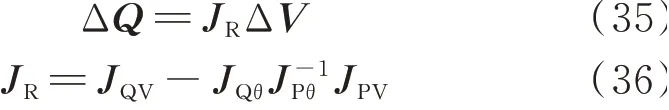
式中:JR为收缩系统雅可比矩阵,其直接体现了节点电压和节点注入无功功率之间的关系,如式(37)所示。

式中:J-1R为收缩的V-Q雅可比矩阵,其第i个对角元素为节点i的V-Q灵敏度。
采用式(19)中考虑环境因素的雅可比矩阵代替式(35)中的雅可比矩阵,得到考虑环境因素的负荷节点V-Q灵敏度表达式如下:

式中:S为计算PV 节点的V-Q灵敏度。
在实际电力系统中,重负荷经常会导致电压不稳定现象的发生。为研究随负荷水平变化时改进模型与传统模型计算的差异性,将参数λ引入式(39),表示每个节点增加注入功率的百分比,模拟重负荷情况下电力系统的电压情况。增加后的功率平衡方程如式(39)所示。
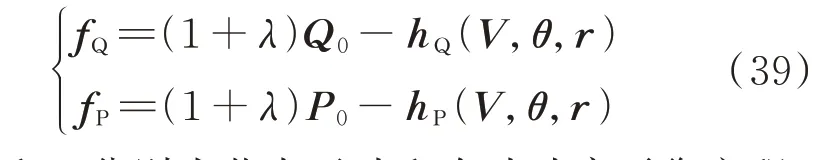
式中:fQ和fP分别为节点无功和有功功率平衡方程;Q0和P0分别为节点的基本无功和有功功率;hQ和hP分别为相连节点向该节点传输的无功和有功功率的和。λ=0 表示无额外增加注入功率,λ>0 表示增加了一定百分比的功率,此时电力系统为重负荷运行。
由于考虑了环境因素,改进的V-Q灵敏度可能不同于传统模型得到的值。本文利用式(40)定义了2 种方法计算结果的误差比例MS。
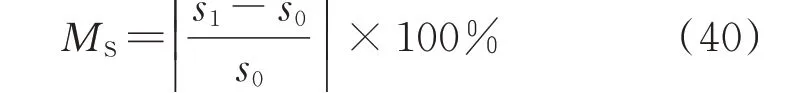
式中:s0和s1分别为传统模型和改进模型求得的灵敏度。
3.2 算例分析
本节采用IEEE 14 节点测试系统作为算例,线路1 为平衡节点,线路2、3、6、8 为PV 节点,其余节点为PQ 节点。电网线路环境参数基准值如表1所示。
基准情景:不考虑输电线路沿线环境条件的变化,即利用常规潮流模型进行计算。
情景1:参考文献[4]设置极端寒冷的情况,输电线路沿线环境温度很低,风速较高。本文选取环境温度为-40 ℃,风速为18 m/s,海拔高度为10 m。
情景2:参考文献[5]设置极端炎热的情况,输电线路沿线环境温度很高,风速很低。本文选取环境温度为50 ℃,风速为0,海拔高度为4 000 m。
针对3 种情景,采用传统模型和改进模型计算电网不同节点的V-Q灵敏度。
附录A 图A5 展示了3 种情景下V-Q灵敏度的对比结果。情景1 和情景2 的情况下,线路14 计算得到的MS分别为2.35%和7.34%,线路12 的MS分别为2.10%和7.46%。由图A5 可得,改进模型与传统模型计算得到的V-Q灵敏度存在很大差异。这说明不能忽略环境因素对电力系统静态稳定性分析的影响。
为了比较2 种模型重负荷情况下的计算差异,利用式(39)对每个节点注入的有功功率和无功功率增加一定百分比。在3 种情景下,通过改变λ值,模拟系统重负荷运行,计算得出MS如图5 所示。
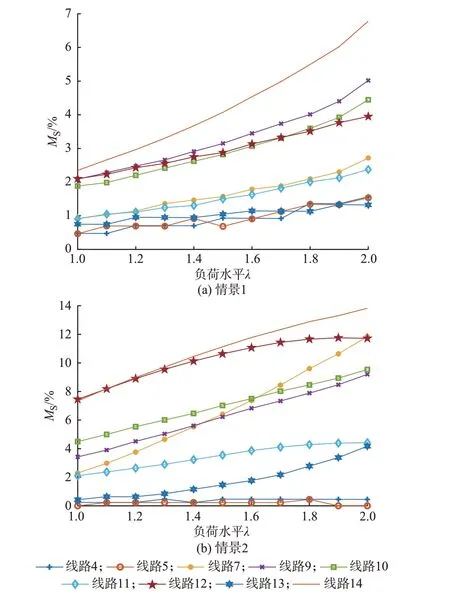
图5 情景1 和情景2 不同负荷下误差结果Fig.5 Error results of scenario 1 and scenario 2 with different loads
观察图5 可得,节点MS随着λ变化而变化。当λ达到2.0 时,线路14 误差比例最大,其情景1 下误差比例为6.78%,情景2 误差比例为13.83%。结果表明,系统负荷不断加重时,改进模型与传统模型计算V-Q灵敏度的误差具有扩大的趋势。
4 结语
本文研究了考虑环境因素影响的电网传输特性计算及灵敏度分析方法,并通过算例分析验证了其有效性,结论如下:
1)提出了一种考虑环境因素的电热耦合统一潮流计算模型,并通过算例分析得出风速、海拔高度及环境温度改变都会导致电网传输特性发生改变,并且环境温度对其影响最为显著。
2)采用Pearson 相关系数衡量出不同位置日平均温度具有时空关联特性,并依据夏季和冬季典型日数据,仿真分析得出电网功率传输特性季节差异明显。
3)提出了计及环境因素的V-Q灵敏度分析方法,对比分析表明改进模型能够更加精准地计算系统节点的V-Q灵敏度。特别是重负荷情况下,两者计算误差显著增大。
本文重点研究环境因素对电网传输特性的影响,未考虑环境因素对源荷的影响。下一步研究将考虑环境因素对电网源网荷的影响,并分析其对电网静态电压稳定性的影响。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

