基于T型微通道结构的微滴生成技术研究

张宁，朱海焕，郭旭，司远，宫平

（长春理工大学 生命科学技术学院，长春 130022）

微流控技术是在芯片中设计微米及纳米级别的流道，在微观角度通过对流道内流体的操控实现对样品的检验与分析，最早在1990年由瑞士 Ciba-Geigy公司的 Manz和 Widmer［1］提出，目前已经广泛应用于化学和生化分析、药物筛选、蛋白质结晶、化学合成和反应动力学研究等领域，与传统生化实验室的检测过程相比，具有体积小、消耗少、反应快的优点［2］。

不同的研究样品对微流控的流道设计尺寸及形状、液滴微流操控提出了不同的要求。互不相溶的两相流体相包裹产生分散液滴，基于这一原理在连续微流控上发展出了液滴微流控［3］。液滴微流控已经应用于数字PCR和流式单细胞分选等领域。由于液体表面张力和流体的剪切速率的影响，会在两相互不相溶或部分相溶的流体界面处形成微滴。根据流体不同，分散相和连续相可以是油相也可以是水相。因此液滴可区别为两种，一种是W/O型液滴，水相在油相中，另一种是（O/W型液滴），油相在水相中［4］。在分子诊断方面，微滴式数字PCR检测方法不仅能实现快速检测，还具有高特异性、高灵敏度的优势，能够满足临床应用需求［5］，微滴式数字PCR对微滴的尺寸和稳定性要求很高，可以通过有限元分析的方法建立微流控流场模型，进而分析微流道结构、驱动条件与生成微滴的关系，用于设计并优化微流控芯片结构，对实现微滴式数字PCR临床应用具有重要意义。

1 原理及模型建立

微滴是由微流控芯片中的两相流体产生，流体间具有部分互溶或互不相溶的特性。两相互不相溶的液体，其中一相作为连续组，另一相为分散组。分散相在连续相中以微小单元的形式存在，通常每个微小单元在10-15～10-9L，在这个过程中形成大量液滴。微流控液滴可以在电磁、离心力的影响下生成，但是通过对微流控芯片结构的改变，即使没有外界“力量”干预也可以生成液滴。这种不需要外部能量的液滴制备方法又称为被动式液滴制备法，可分为三种，包括T型通道法、流动聚焦法和共轴流聚焦法［6］，如图1所示。主动法包括电驱动法和光驱动法等。

图1 三种被动产生乳液微滴的方法

T型通道法由Thorsen最先提出，具体实现方法是在压力和剪切力的作用下，两相互不相溶的液体在T型管道交叉口处相遇时，流动相截断分散相，从而形成液滴。该方法是目前产生微流控液滴的最基础方法之一。

1.1 有限元分析法

有限元分析方法涉及到的单元、节点数目都是有限的，被称为有限元分析法［7］。其分析步骤大致可分为：

（1）仿真参数设置，包括定义实际问题的几何计算模型、划分网格单元，整理分析对象的材料信息、载荷信息、约束信息、单位节点信息等。该处理的中心任务就是由实际问题建立分析模型，为数值计算做准备。

（2）流道仿真计算，在层流模型下对T型微流道进行仿真，包括边界条件计算、流体特性计算等。

（3）计算结果分析，对计算结果进行可视化处理。

1.2 水平集方法理论

水平集方法（Level Set Method，LSM）最初在1980年左右由数学家开发，是流体力学建模和运动目标计算追踪的有力工具。其基本思想是将二维曲线的演化问题转化为三维曲线的演化问题，目标运动速度计算方程也会随之拓展到更高维度。同时运动速度的法向量变化会引起曲线几何形状的变化，继续建立和计算水平集函数。根据建立的随着时间变化的水平集函数，计算并取得形状变化参数，包括界面形状、法线方向、最后曲率等［8］。如图2所示，一个具有良好边界条件的有界区域，平坦的蓝色区域代表x-y平面，红色的外面图形代表水平集函数φ，形状的边界是φ的零水平集，而形状本身是平面上φ为正（形状内部）或零（边界处）的点集。

图2 水平集法分割图和零等值面

水平集函数的一般求解步骤如下：

（1）初始化：该过程为求解水平集方程提供准备，包括初始化函数及物理量。

（2）求解对应水平集方程：根据水平集方程的特定形式，在下一个时刻获得一个与水平集函数相对应的数值，而这时产生新的边界，同时也对应着水平集函数的零等值面。

（3）初始化新的水平集函数：为了更方便和快捷地解决问题，始终维持水平集函数的相应连续性具有重要意义。

（4）相关物理量控制方程的求解：由下一时刻物理量的结果值来求解该时刻的控制方程。

（5）进入下一个时刻的计算，重复步骤（2）～步骤（4），直至满足计算的要求。

1.3 动量守恒定理

在微流道的流动计算和仿真过程中，流道中的流体被视为一个整体的计算领域，对于任何时间t，通道中流体的质量m和受到的总力F，液体的流速是。图3是基于动量定理的分析模型示意图。在Δt之后的时间区间内，满足动量定理：

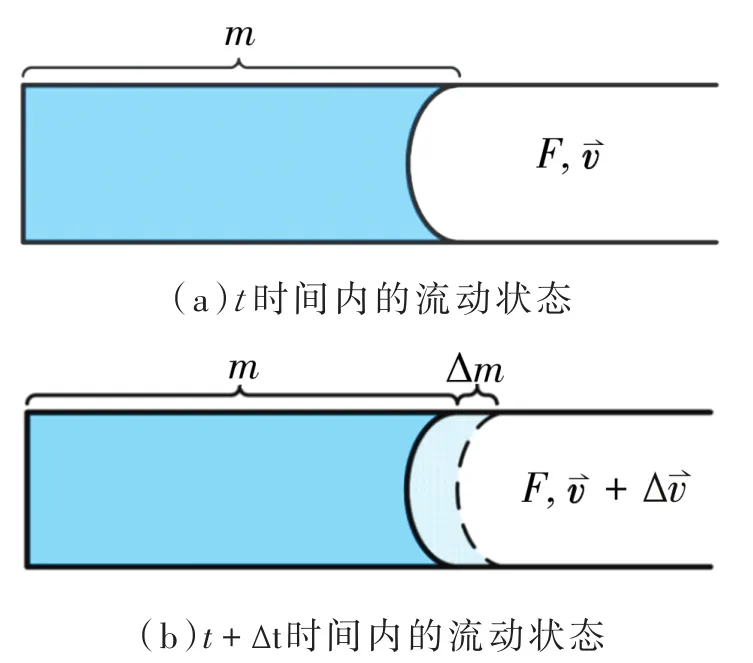
图3 基于动量定理的分析模型示意图

在这Δt时间间隔，流道中的流体速度变化为。

在公式（1）中，微通道中气体/液体的表面张力Fσ和流动微通道壁面产生的阻力Fμ的合力构成了流体的总作用力F：

通过迭代求解每个时间间隔Δt内流速Δv⇀的变化，可以得到流速随时间的变化规律［9］。

1.4 基于雷诺方程的壁面阻力推导

微流芯片的大多数微通道具有矩形横截面，并且大部分为宽度大于深度的狭缝通道。流体在这种微通道内流动时为层流，在这种情况下可忽略体积力的影响，且微通道壁面无滑移现象，这种流动符合雷诺方程［10］的基本假设。因此，采用与雷诺方程相似的方法可推导微通道壁面阻力的计算过程。图4为流道内的流速分布图。

图4 流道内的流速分布图

根据牛顿黏度定律［11］，由二维雷诺方程可知，当上下界面为固体壁面且无滑移时，流体微元在x方向任意点的速度为：

式中，h为上表面与下表面形状函数之差，可表示为：

将式（4）代入式（3）中，可以得到界面的剪应力τw为：

微流体流动过程中，流动阻力（摩擦）Fμ流墙表面的流体可以表达为沿微通道x方向各dx微单元壁面剪应力τ的积分。

入口处的边界条件满足以下要求：

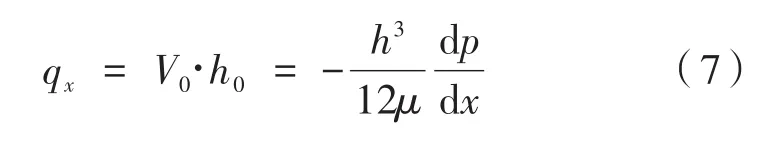
流壁表面对流体的流动阻力Fµ可通过以下方式获得：

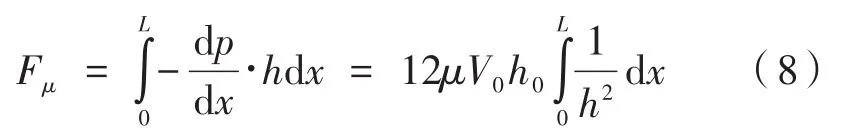
式中，V0为流体的速度；h0为入口通道的高度。基于动量定理的微流道原理图如图5所示。

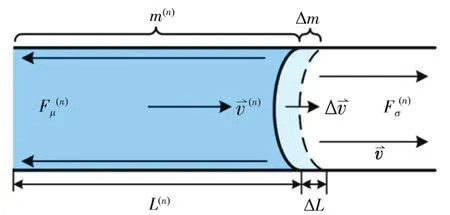
图5 基于动量定理的微流道原理图

应用动量定理的每次Δt，流道中的流体速度变化的时间间隔内Δt，经过n次迭代运算和积累，有：

在公式（9）中，得出：

1.5 模型的建立

建立数学模型是模型仿真的关键，必须在仿真之前定义相应的模型边界条件以及初始值，这样可以减少模拟仿真过程中的误差并达到想要的结果。在微滴运动的模型仿真研究中，对模型做出如下假设：

（1）两相液是不可压缩的牛顿流体，重力对本实验的影响结果忽略不计；

（2）流体特性稳定，不随时间改变；

（3）液相流率稳定，不随时间改变。

通过对雷诺数Re的介绍，微通道内的流体流率非常低，例如样本（水），在宽度和深度都为100µm的微通道结构内，水的流率约为200µm/s时，计算得出雷诺数Re约为4×10-3，远远小于10，所以惯性力可以忽略不计，微通道内表现出稳定的层流流动。

在Comsol软件的仿真中，微通道中的微滴运动模型选用的是层流两相流的水平集界面（Laminar Two-Phase Flow，Level Set interface）模型，根据“水平集”和“层流”的不同特性，可以分别建立出水平集方程和动量传递方程与连续性方程，因此该水平集界面由以下方程共同确定：

式中，ρ是密度（单位 kg/m³）；Fst表示表面张力（单位N/m³）；u代表流率（单位m/s）；μ代表动力粘度（Pa·s）；Φ则表示水平集函数。利用Φ =0.5来代表两相流的边界，也就是液滴的表面（Φ =0处代表分散相，Φ =1处代表连续相），可以通过以下公式来计算边界处的密度ρ和动力黏度系数μ。交汇界面处的密度ρ及动态黏度系数μ可由以下方程确立：

其中，ρ1、ρ2、μ1、μ2分别为油相、水相的密度及动力黏度系数。

微流道中流动的模拟模型如图6所示，在此模型中，通道截面为矩形，通道截面的纵横比为1。微通道管壁的疏水性强弱与接触角有关，其中接触角为135°，表示为疏水管壁。流体分别为油相和水相，油相材料Mineral Oil密度是ρ1=1.614× 103kg/m3，动力黏度是μ1=1.24× 10-3Pa·s；水相材料Water密度是ρ2=1 × 103kg/m3，动力黏度μ2=8.9×10-4Pa·s。液相入口预设分别为充满油相及水相。

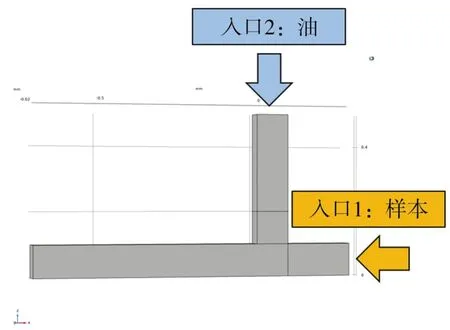
图6 微流道的几何模型

微滴的有效直径deff计算见公式（19），Ω表示微滴可能存在的微结构x小于0 mm的水平通道区域。

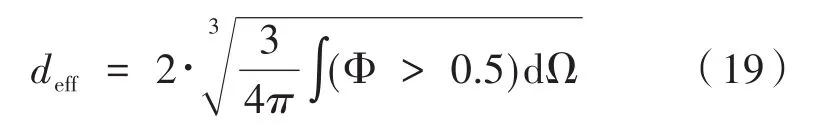
2 仿真结果分析

2.1 通道结构对微滴直径大小的影响

T型微流通道内的微滴生成类似于传统乳化过程，但是更微小化。在负压条件下，连续相（Mineral Oil）流入T型结构的水平微通道，分散相（Water）流入T型结构的垂直微通道。在T型通道的水平和垂直通道交界处，连续相（Mineral Oil）和分散相（Water）交融界面由于表面张力小于连续相（Mineral Oil）的剪切力，便自发形成微滴。其中微滴生成的频率与连续相和分散相的流速有关。

流道仿真计算结果如图7所示，在水相通道直径一致、负压驱动一致、管壁性质一致时，仅改变输样通道的宽度大小，可得到不同直径的微滴。宽度为0.1 mm的输样通道生成的微滴直径约为110µm，通道宽度为0.13 mm的载样通道生成的直径微滴约为130µm。仿真结果显示，在油相所在微流体通道尺寸保持不变的情况下，水相所在的微流体通道宽度越大，油相相对于水相的流阻越大，油相的流速便会越慢，对应现象是生成的微流体积变大。因此不同尺寸的微滴，可以通过调节油相或水相微通道的宽度尺寸控制，即水相的通道宽度越大，微滴生成尺寸越大。

图7 通道直径对生成液滴尺寸的影响

2.2 液相流率对微滴直径大小的影响

两相流速、黏度、表面张力、微通道尺寸、微通道结构等因素都会影响微通道内生成液滴的尺寸大小。在微滴生成用油和微通道选用恰当的情况下，两相流体的流速及相对流速是影响微滴生成的重要因素。在两相流体速度不同时对微液滴生成尺寸进行数值分析，进而得出流速V1、V2（单位：10-3m3/s）与液滴尺寸的关系，液滴的有效液滴直径表示为deff（单位：µm），频率为f（单位：Hz）。液滴的有效液滴直径随不同两相流速的变化如图8所示，液滴的生成速率随两相流流速的变化如图9所示。

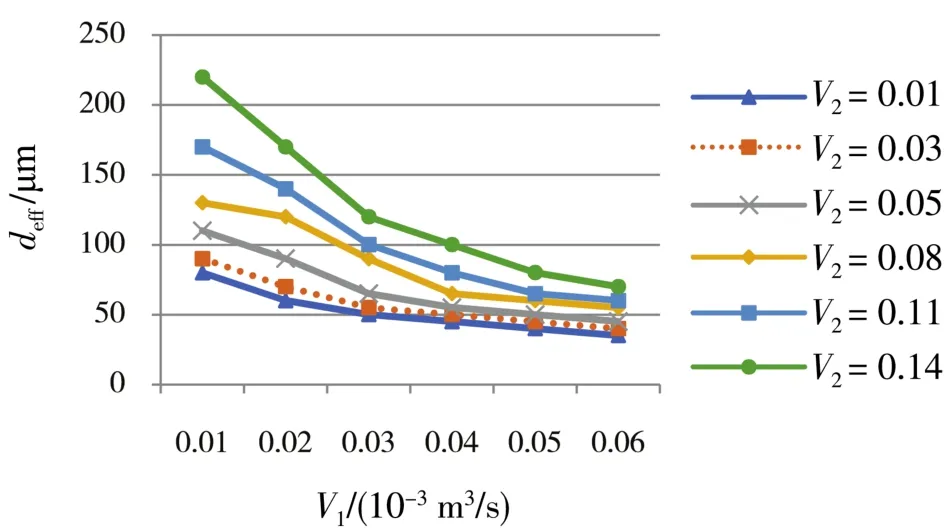
图8 微滴有效直径随两相流流速的变化

图9 微滴生成速率随两相流流速的变化

在T型结构微流道中，当离散相流体速度一定时，在微通道交汇界面连续相对离散相的表面张力与连续相流速成正增长，进而使离散相的膨胀过程变短，生成的尺寸变小，液滴生成频率升高。当连续相流速增加到一定程度时，连续相和离散相的流速对微液滴的尺寸影响变弱，但对液滴生成频率的影响越来越大。相反，当连续相的流体速度一定时，生成微液滴的尺寸随着离散相流速的增加而变大，液滴生成频率升高。

3 实验测试

为了验证所提出模型的可用性，设计制造了具有相关结构的微流控芯片，并采用微滴的负压生成方式对其微滴生成过程进行测试。微流控芯片采用COC材质，便于光学观察，采用指定的接触角和接触表面。最后采用微滴芯片阅读仪器对微流控芯片中生成的微滴进行测量。

3.1 微滴生成芯片

两相流的运动状态由微滴型微流控芯片管壁的浸润特性决定，对微滴形成具有重要影响。若生成油包水型微滴，需要管壁具有较强的疏水特性。为增强管壁的疏水能力，本文采用了表面活性剂-含氟硅烷等化学试剂对管壁进行处理。

根据理想模型，加工出的生成芯片输油通道内径分别为102µm、103µm，样本通道内径为101µm、133µm，其理想内径尺寸分别为100×100µm和130×100µm，内径误差可以控制在10µm以内。测量微通道深度分别为99.4µm、100.6µm，几乎完全满足理想的沟槽深度100µm。图10给出了加工完成的微滴生成芯片的成品效果图。

图10 芯片成品效果图

3.2 负压生成系统组件

负压系统用于产生生成微滴所需的稳定负压驱动，其主要组成部分包括微动气泵、压强传感气体容器、压力输出控制系统以及电磁阀组成，负压方式示意图如图11所示。其中，气体容器-压力传感器-负压输出控制装置-真空泵/电磁阀在STM32最小系统的控制下构成了一套闭环的负压控制系统。负压生成系统可以接受微处理器的指令而达到预定的压力参数保持稳定。原理样机如图12所示。

图11 微滴负压方式示意图

图12 微滴负压方式原理样机图

3.3 微滴生成测试

在微流控芯片上进行了微滴生成的测试。连续相和分散相分别为油相和水相，油相材料Mineral Oil密度是ρ1=1.614 × 103kg/m3，动力黏度是μ1=1.24× 10-3Pa·s；水相材料Water密度是ρ2=1 × 103kg/m3，动力黏度μ2=8.9 × 10-4Pa·s。将芯片固定在芯片夹具中，芯片夹具如图13所示，用移液枪向芯片入口分别添加油相和液相，微滴生成后将微滴转移至芯片阅读仪的相机下面，采用图像处理的方法对生成的微滴图像进行处理，获得生成芯片的流动特性，并利用高速摄像系统观察实验结果。

图13 生成芯片夹具设计图及实物图

在微滴生成芯片实验中，对生成的微滴数量及质量进行分析，输油通道和样本通道直径为102µm、101µm时，微滴直径约为112µm，生成微滴如图14（a）所示；输油通道和样本通道直径为103µm、133µm时，微滴直径约129µm，生成微滴如图14（b）所示。微滴生成频率和大小与仿真设计结果一致。水相微通道宽度尺寸在100µm条件下，生成的微滴大小为110µm。水相微通道宽度尺寸在130µm时，微滴大小为130µm。

图14 微滴生成图

本文中微滴生成测试证实了T型微通道结构设计方案的可行性、正确性以及科学性。

4 结论

本文提出了一种基于有限元分析法的T型微通道设计方法，建立了一个基于动量定理可以描述微流道内相液的流动特性的理论模型。该模型的相关系数采用有限元分析法，利用Comsol多物理场仿真软件计算得出，从而实现了T型微流道的相液流动分析，为微流控芯片的结构设计提供了一种快速、准确的方法。