一种结合用户适合度和课程搭配度的在线课程推荐方法

胡园园 姜文君 任德盛 张 吉

1(湖南大学信息科学与工程学院 长沙 410082) 2(之江实验室 杭州 310012)

随着互联网技术的快速发展，社会对教育重视程度的提高以及经济水平的不断增长，在线教育行业得到了前所未有的发展[1].与传统教育相比，在线教育突破了时间和空间的限制，降低了学生的时间成本和经济成本.根据iiMedia Research(艾媒咨询)数据显示，2020年第1季度中国在线教育用户规模已达3.09亿人，市场规模达4 538亿元[2].“互联网+教育”[3]的形式使得在线教育用户规模扩大，同时用户对在线教育的认同度和接受度也在不断提升.但与此同时，各种各样的在线课程大量涌现，可供选择的课程种类越来越多.面对如此众多的选择，用户想要从中挑选优质并且适合自己的课程非常困难.因此，个性化课程推荐[4]应运而生.课程推荐算法通过研究用户的选课兴趣、历史选课行为、课程的属性等，向用户推荐其可能感兴趣的课程，从而有效缓解信息过载问题，提升用户的选课效率和在线体验.

课程推荐是在线教育平台中一个关键环节.有效的课程推荐不仅可以提高用户听课率和满意度，而且能够促进在线课程销售，提高平台收入.课程推荐的关键在于精准定位每个用户的学习目标和学习需求，找到最适合用户的课程.已有的课程推荐方法大多基于相似用户或者相似课程，通过构造用户评分矩阵进行推荐.一些研究[5]提出将课程前提关系嵌入神经注意力网络的算法来实现课程推荐，还有一些工作[6]通过研究用户的个性化潜在学习偏好来提高课程推荐的性能.但是，已有课程推荐方法很少关注用户能力与课程的适合度，可能会推荐用户感兴趣但学不会、不合适的课程；也较少考虑候选课程与用户已学课程的搭配程度，可能产生相似课程重复推荐或不当推荐.因此，有效的在线课程推荐需要同时关注不同用户的个性化学习特征(用户适合度)和不同课程之间的关联(课程搭配度).

本文通过研究用户的各种在线学习行为和习惯，如注册课程、观看课程等，探究用户的学习特征和学习适合度；同时，深入挖掘不同课程之间的关联关系，探索不同课程之间的可搭配度；最后，融合用户适合度和课程搭配度，提出改进的协同过滤模型来给用户推荐课程，提高推荐性能.本文试图采用简单易行的方法实现更合适的课程推荐，同时保证较强的可解释性.总体来说，本文主要贡献有3个方面：

1) 深入研究用户的学习特征，分析用户学习成绩特征分布和课程之间的关系，探究用户对不同课程的适合度.

2) 挖掘不同课程之间的关联，并基于关联来评估课程之间的搭配度.

3) 提出了一种结合用户适合度和课程搭配度的课程推荐模型(user-suitability and course-matching aware course recommendation model, SMCR).该模型根据用户适合度和课程搭配度得到最终推荐列表，实现更合适的top-k课程推荐.

1 相关工作

本文主要与学习成绩预测和课程推荐相关.

1.1 学习成绩预测相关技术

Su等人[7]提出了一种新的回归神经网络框架，通过双向长短期记忆(long short-term memory, LSTM)模型学习做题序列和题目信息，并加入自注意力机制来预测得分.Sweeney等人[8]根据学生历史成绩和相关课程资料，提出了一种混合矩阵分解(matrix factorization)和随机森林(random forest)的方法预测学生成绩.Wang等人[9]分析了不同学习行为和学习效果之间的关联，提出了因果关系关联分析算法.He等人[10]提出了基于正则逻辑回归的2种转移学习算法LR-SEQ(sequentially smoothed logistic regression)和LR-SIM(simultaneously smoothed logistic regression)来预测用户学习情况.Dhanalakshmi等人[11]使用基于机器学习技术的有效意见挖掘和排名方法分析学生成绩.

目前课程推荐和学习成绩预测的相关工作通常都是分开独立进行的.而本文通过考虑用户可能的课程成绩或完成度来得到其对某一课程的学习适合度，并基于此帮助用户选择更适合其能力或需求的课程.

1.2 课程推荐相关技术

Jing等人[12]提出了一种基于内容的算法框架，将用户兴趣和课程前提条件关系结合起来，并通过协同过滤进行课程推荐.Apaza等人[13]提出了一种基于大学生历史成绩的课程推荐系统，并使用LDA(latent Dirichlet allocation)主题模型从课程内容中提取相关主题.Ibrahim等人[14]提出了一种基于本体的混合过滤系统框架，结合协同过滤和基于内容的过滤为用户提供个性化课程建议.Farzan等人[15]研究了学生未来职业目标并为学生提供与其职业目标相关的课程建议.Jiang等人[16]提出了一种基于目标的课程推荐算法，根据用户已经学会的知识模型为其推荐合适的一系列相关的课程.Zhang等人[17]提出一种分层强化学习算法，用以修改用户个人资料，并且能够根据修订后的个人资料调整课程推荐模型.Parameswaran等人[18]为学生推荐既满足其课程修读要求又符合其学习兴趣的课程.Aher等人[19]结合聚类技术和关联规则算法来为刚学习某些课程的新学生推荐课程.

整体来说，已有的学习预测和课程推荐方法主要基于用户和课程之间的交互信息进行模型设计，但是通常忽略了用户的学习适合度和课程之间的搭配度，可能导致课程推荐准确性低或者学习效果不佳.基于上述调研和分析，本文结合用户适合度和课程搭配度来综合得到课程的推荐度.

2 问题定义及整体方案和数据描述

本节首先给出关键概念，然后给出形式化的问题描述，最后简要介绍本文的解决方案.本文用到的符号如表1所示：

Table 1 Symbol Table表1 符号表

2.1 相关概念

定义1.用户适合度.用户适合度表示某用户对于某课程的学习适合程度.

定义2.课程搭配度.课程搭配度表示2个课程可以进行搭配的程度.

定义3.课程推荐度.课程推荐度表示该课程值得推荐的程度.根据定义1和定义2中的学生适合度和课程搭配度，将二者结合起来，按照一定的方式进行综合计算.

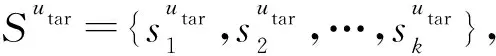
2.2 方案概述

本文解决方案主要包括3个模块，如图1所示.

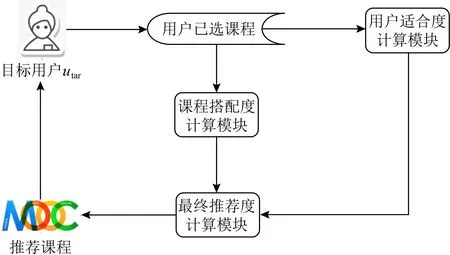
Fig. 1 The overall framework of the SMCR model图1 SMCR模型整体框架

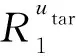
模块2.课程搭配度计算模块.通过挖掘课程之间的关联关系，计算出课程之间的搭配度.4.2节将介绍该模块的详细内容.

模块3.最终推荐度计算模块.将上述2个步骤中得到的用户适合度和课程搭配度按照一定比例进行结合得到最终推荐度，并根据该推荐度实现课程top-k推荐.4.3节将介绍该模块的详细内容.

2.3 数据集及预处理

本文使用2个在线学习平台的数据集来探索用户适合度和课程搭配度.一个是CN(canvas network)数据集[20]，包含了Canvas Network开放课程平台2014年1月至2015年9月的学习记录，包含每个用户的选课记录及相关课程属性.另一个是学堂在线平台公开的中国大学MOOC(massive open online courses)学习数据[21]，其中包括学生id、第1次注册课程的时间、课程id等属性.具体统计信息如表2所示:

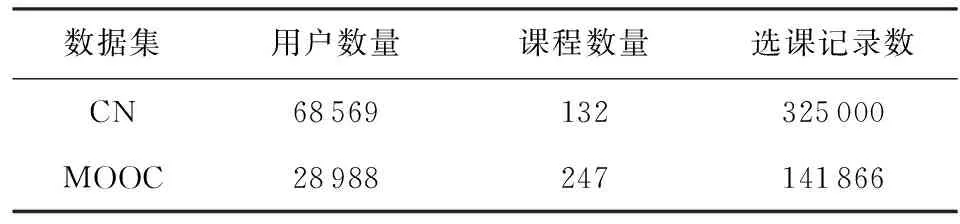
Table 2 Introduction of Dataset表2 数据集介绍

CN数据集还包含了课程类别信息，如表3所示:

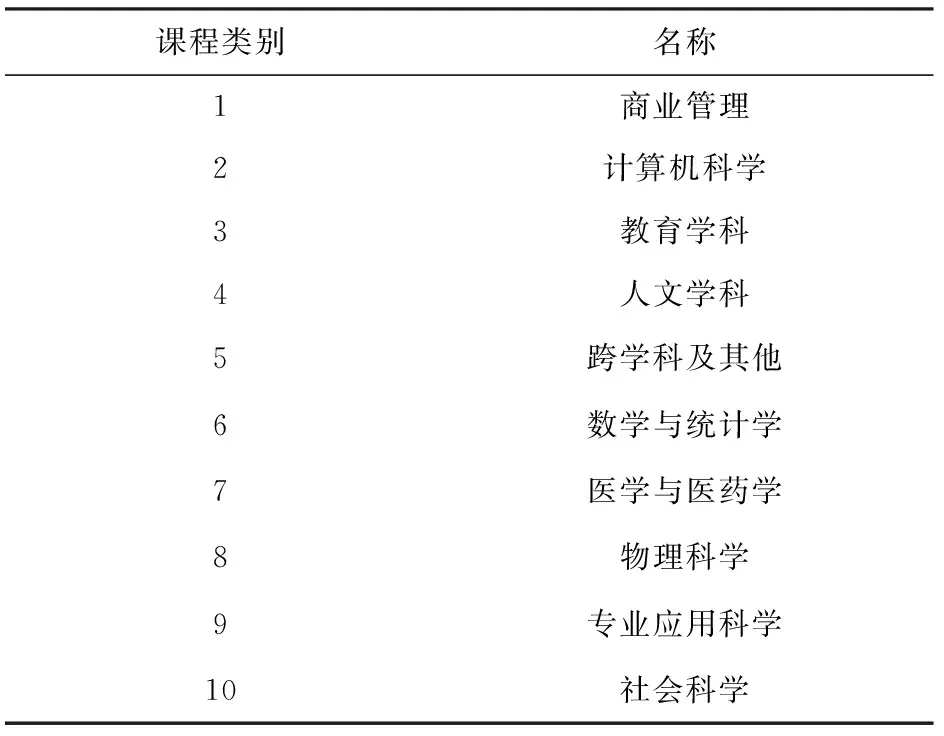
Table 3 Different Category Names of Courses on CN Dataset表3 CN数据集上不同课程类别名称

在进行分析和实验之前，需要对数据集进行预处理，包括清除数据集中成绩为空值的记录，并去除重复值.同时，需要过滤掉仅选1门课程的用户.另外，数据集中的成绩进行了归一化处理，即成绩分布在[0,1]范围内.

3 数据分析

本节主要分析用户的不同学习行为和学习类型，探究用户的学习需求；研究用户适合度和课程成绩之间的关系，分析了课程成绩对课程推荐的影响.这些分析可以帮助了解用户的学习意图，同时能够提高课程推荐的准确性.

3.1 用户学习类型分析

首先统计在线学习平台中用户历史所学课程的类别分布，来判断其学习类型.图2展示了CN数据集上2个典型用户的课程类别分布.

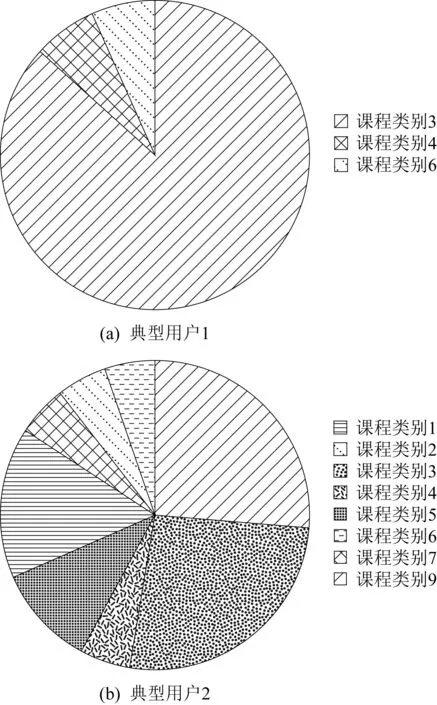
Fig. 2 Course selection for two typical users on CN dataset图2 CN数据集上2个典型用户的课程选择情况

图2(a)中用户选择的主要课程所属类别为教育学科，课程类别为人文学科和数学与统计学所占比较少，说明该用户更重视专业课的学习，更专注于教育学科类别的课程学习.图2(b)中用户所选课程的类别比较丰富，说明该学生的课程兴趣分布较为广泛，课外兴趣比较浓厚.

接着，统计数据集中用户的学习状态，如图3所示.图3(a)展示了用户学习状态的分布情况.可以看到，学习类型为积极型的用户数量最多，其次是学习类型为被动型的用户数量，说明大多数用户有着明显的学习者类型区分，有积极型的，也有消极型的.

图3(b)表示的是用户1周中希望学习的时间分布.从图3(b)中可以看到，每周学习2～4 h是大多数用户希望的学习时长，其次是每周1～2 h和每周4～6 h.这说明大多数用户都有比较积极的学习行为，希望学习时长分布也符合实际情况.

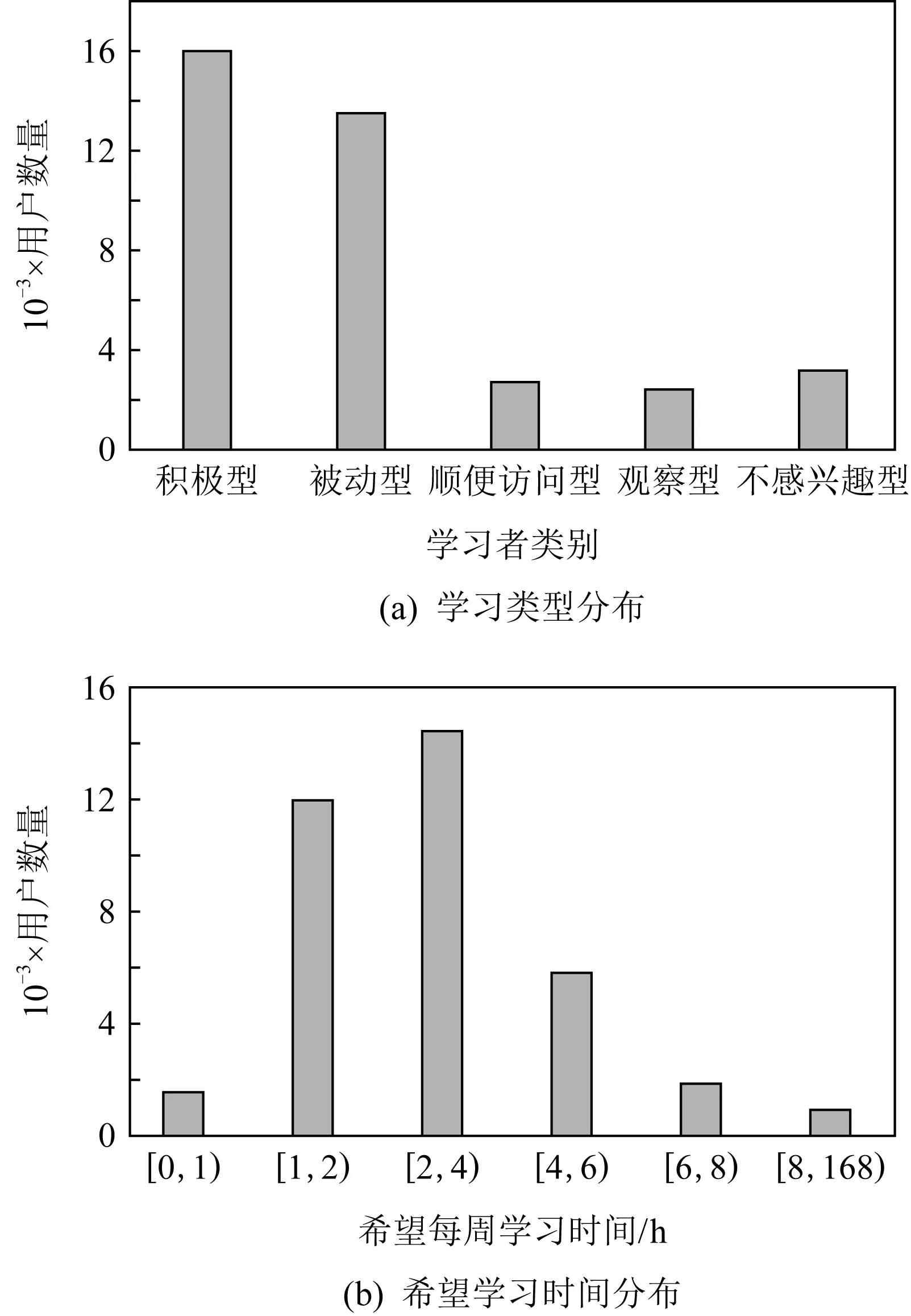
Fig. 3 Course selection for different types of users on CN dataset图3 CN数据集上不同类型用户的课程选择

图4表示的是CN数据集中每个类别的选课人数分布.从图4可以看到，不同类别的课程选课人数是不同的，其中选择“专业应用科学”类别的选课人数是最多的，其次是选择“人文学科”和“教育学科”类的人数.图5表示的是MOOC数据集中所有课程的选课人数分布.大多数课程的选课人数都在500～1 000之间.图4和图5表明不同类别或者不同课程的选课人数是有差别的.

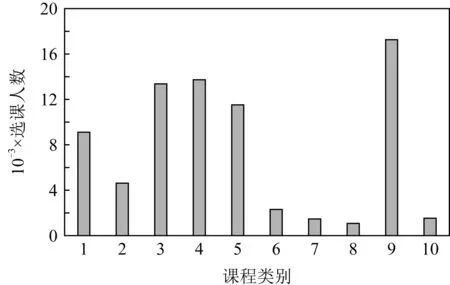
Fig. 4 Number of users for different categories of courses on CN dataset图4 CN数据集上不同类别课程的选课人数

Fig. 5 Number of users for different courses on MOOC dataset图5 MOOC数据集上不同课程的选课人数

3.2 用户适合度分析

一般来说，用户学习适合自己的课程通常应该得到较高的成绩.因此，本文主要根据成绩来分析用户对不同课程的适合度.分别从课程类别、单个用户的平均课程成绩等方面对用户的所选课程成绩进行分布统计，挖掘用户适合度的相关因素和影响.

图6展示了CN数据集中不同类别课程的成绩分布情况.图6(a)展示了每个课程类别的平均成绩分布.不同类别的课程平均成绩各不相同，说明课程成绩与课程所属类别有关.其中，类别为“人文学科”的课程平均成绩是最高的.

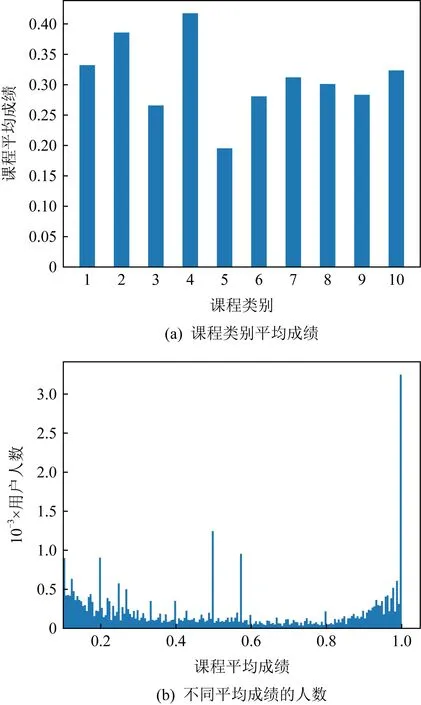
Fig. 6 Average grades by course category and user number distribution of average grades on CN dataset图6 CN数据集上各类课程平均成绩及用户平均 成绩人数分布

图6(b)表示的是关于不同课程平均成绩的人数分布.这表明每个平均成绩分布段的人数频率.每个平均成绩段的人数主要集中于500人以下，这说明用户的平均学习成绩分布范围较为广泛，不同学生因适合程度、努力程度等的不同，所得到的学习成绩也相应不同.

图7展示了CN数据集中不同成绩段的用户“观看”和“交互”所有不同课程的人数分布情况.图7(a)是不同课程成绩段分布的用户观看该课程的人数.其中，“观看”行为的值为1表示用户与课程的互动，即观看课程视频；而“观看”行为的值为0表示用户与该课程并未有互动.从图7(a)中可以看到，随着课程成绩的提高，观看课程视频和未观看课程视频的人数比值在不断上升，这表明观看课程视频对于取得较高成绩有一定的促进作用.另外，成绩在0～0.2的用户数量最多，表明在线课程的完成率整体偏低.这也从侧面反映了考虑用户适合度对在线课程推荐具有非常重要的意义.

Fig. 7 Number of “viewed” and “explored” users in different grades on CN dataset图7 CN数据集上不同成绩段“观看”和“交互”人数

图7(b)展示了“交互”属性与用户课程成绩之间的关系，“1”表示用户与该门课程有交互行为，而“0”表示用户与该课程没有交互.从图7(b)中可以看到，在每个成绩段，没有进行课程交互的人数要大于进行了课程交互活动的总人数.该现象再次反映了很多用户对在线课程的学习投入不够，整体参与度较低.因此需要改进课程推荐，考虑用户适合度，从而有望提升用户参与度.

图8(a)和图8(b)分别表示MOOC数据集中不同课程的辍学率分布情况以及用户的辍学率整体分布统计.在该数据集中，是否辍学统一由0和1来表示.可以看到，大多数课程的辍学率集中分布于0.7～0.9之间.而对于用户来说，辍学率在0.8～1区间的人数最多.该数据分析结果表明，现有在线学习平台的整体学习情况亟待改善，而本文考虑通过用户适合度来改进课程推荐就是为此目的.

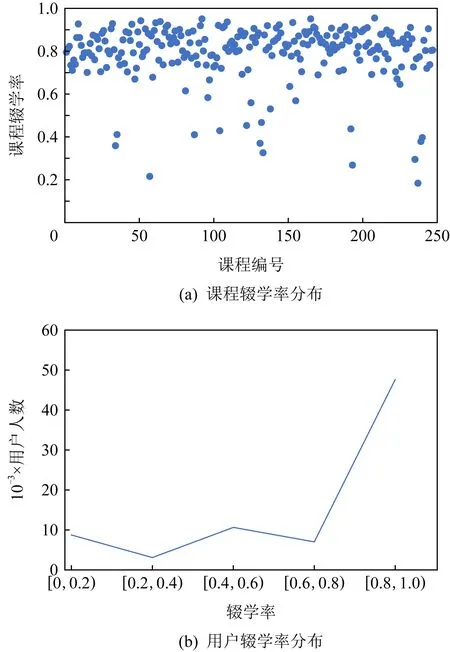
Fig. 8 Distribution of dropout rate for courses and users on MOOC dataset图8 MOOC数据集上课程辍学率和用户辍学率分布

3.3 课程搭配度分析

一般来说，不同课程之间是有关联关系的,不同课程之间的搭配关系也是不同的.因此，需要根据课程之间的关联关系来分析不同课程之间的搭配度.

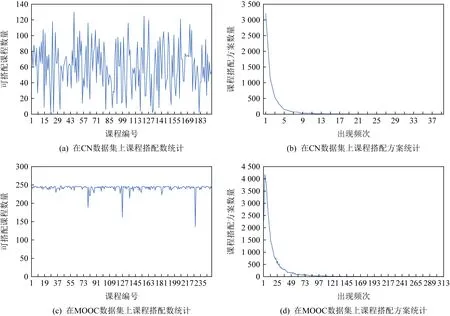
Fig. 9 Number of courses and collocation statistics图9 课程搭配统计

图9(a)展示了CN数据集每门课程可搭配的课程数量.从图9(a)中可以看到，每门课程可以实现搭配的课程数量在0～120之间，这说明不是所有课程之间都可以进行搭配.同时，图9(a)中也显示有少数课程可以实现的搭配课程数量较多，可能该课程为基础课程或者科普类课程，说明学习该课程的人数比较多，课程比较受欢迎.

图9(b)展示了CN数据集课程搭配方案的频率分布情况.将2个可以进行搭配的课程看作是一个课程搭配方案，图9(b)统计了每个课程搭配方案出现的次数.根据统计结果，大多数课程搭配方案出现的次数较少，基本都在10次以下.这表明相当多的课程搭配方案出现频率都不太高，说明在线用户选课具有较强的自主性和一定的随意性.正因为如此，合适的课程推荐需要考虑候选课程与用户已学课程之间的搭配性，因为并不是任意2个课程之间都可以实现搭配.

图9(c)展示了MOOC数据集中每门课程可搭配的课程数量.从图9(c)中可以看到，每个课程可搭配的课程数量主要分布在200～250之间，比图9(a)中每门课程可搭配的课程数量要多.

图9(d)展示了MOOC数据集中课程搭配方案的频率统计分布.可以看到，大多数课程搭配方案出现的次数都在50以下.该数据集较CN数据集的可搭配课程数量更多.

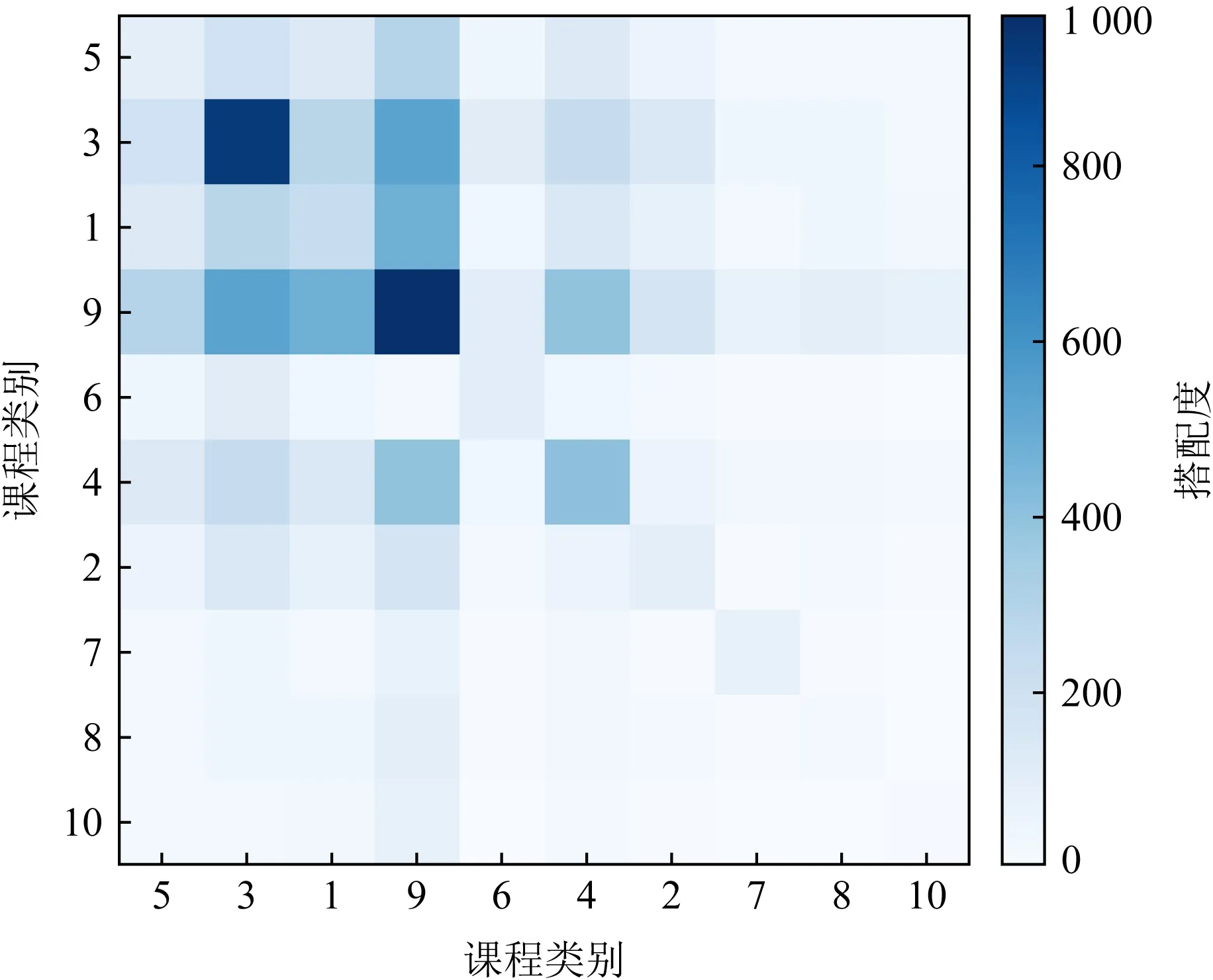
Fig. 10 Statistics of collocation courses between two categories on CN dataset图10 CN数据集上2个类别之间的可搭配课程统计

图10展示了CN数据集中2个类别之间的可搭配课程统计.颜色越深，表示这2个类别之间可以搭配的课程数比较多，类别的课程搭配度较高；颜色越浅，则表示这2个类别之间的可搭配课程较少，类别的课程搭配度较低.可以看到，一般情况下，属于同一类别的2个课程之间可搭配度较高，不同类别的2个课程之间可搭配度相对较低.但也有一些类别与其他多个类别课程的搭配度都较高，比如类别9.

3.4 总 结

从3.1～3.3节的数据分析发现：

1) 不同用户的学习类型不同；学习成绩能够反映用户对课程的学习适合度.一般来说，用户某门课程的成绩越高，表明用户对该课程的适合度就越高.很多用户对在线课程的学习投入较少，课程完成度较低.因此需要改进课程推荐，考虑用户适合度，从而有望提升用户参与度，改进在线学习效果.

2) 课程之间是有一定关联关系的.每门课程的可搭配课程数是不同的；并不是任何2门课程都可以进行搭配；相同类别的2门课程之间可以进行搭配的可能性较高.另外，在线用户选课具有较强的自主性和一定的随意性.因此，合适的课程推荐需要考虑候选课程与用户已学课程之间的搭配性，从而提升课程推荐的效果.

4 基于用户适合度和课程搭配度的推荐方法

本文提出了一种结合用户适合度和课程搭配度的课程推荐模型SMCR，该模型主要由2个部分组成：一是通过用户-课程相似度矩阵和已学课程成绩，计算用户对候选课程的适合度；二是挖掘课程搭配频繁项集，计算课程之间的搭配度.将这2部分融合起来，形成最后的课程推荐.

4.1 计算用户适合度

本文使用基于物品的协同过滤思想来计算用户对课程的适合，这是一种基于最近邻的推荐算法，主要基于如下现象：用户倾向于喜欢与其历史行为记录相似的物品.在推荐系统中，该算法通过计算物品之间的相似性，从而给用户推荐与其历史最接近的物品.但该算法未考虑候选产品是否真正适合用户，本文对此进行了改进.本文首先计算课程之间的相似度，然后基于相似度和已学课程成绩计算目标用户对候选课程的适合度.

1) 根据目标用户utar的学习行为，构建用户-课程学习成绩矩阵.利用基于物品的协同过滤推荐算法，计算目标用户utar的已选课程ci与未选课程cj之间的相似度W(ci,cj).计算公式为

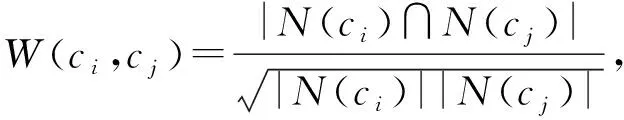
(1)

其中，N(ci)和N(cj)分别表示选择了课程ci和课程cj的用户集合.

2) 根据相似度选出与目标用户utar已选课程集合中每一门课程相似的前l个课程，作为候选课程.计算目标用户utar对于候选课程列表中每一个候选课程cj的适合度P(utar,cj).找出与候选课程cj相似的已选课程，根据目标用户在这些课程中的成绩来衡量其对候选课程cj的课程适合度.P(utar,cj)计算为

(2)

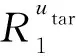
4.2 计算课程搭配度

本文使用关联规则来计算任意2个课程之间的搭配度.基本思想是：频繁被用户共同选择的课程通常是有较高的搭配度[22].例如，同时选择学习《C语言》和《数据结构》的用户比同时选择学习《C语言》和《西方经济学》的用户要多，即已学习《C语言》的用户更倾向于选择《数据结构》，而不是《西方经济学》，因此《C语言》与《数据结构》的搭配度更高.本文首先计算2个课程同时出现的概率(即支持度)，筛选出支持度高于设定阈值的所有候选课程对；然后，计算其置信度作为课程之间的搭配度.具体如下.

关联规则是描述数据集中数据项之间存在的内在关系的规则.一般来说，关联规则的挖掘主要分为2个步骤：1)找出目标数据集中所有的频繁项集；2)利用这些频繁模式产生符合条件的关联规则.本文主要通过FP-growth算法来挖掘课程之间的关联规则，该算法通过构建一个“FP树”来存储数据集中的所有数据，并且从中挖掘出数据集中存在的频繁项集或者频繁项对.

首先，通过FP-growth算法挖掘所有课程中频繁共同被选的课程对，构造课程与课程之间的搭配.搭配度大小可以通过支持度和置信度衡量.将用户同时选择课程ci和课程cj的情况看成一个搭配课程对，该课程对出现的频率即支持度support(ci,cj)，筛选出支持度高于一定阈值的所有候选课程对.支持度计算为

(3)

其中，|N(ci)∩N(cj)|表示同时选择课程ci和课程cj的用户数量，|N(U)|表示数据集中进行了选课行为的所有用户数量.

然后，对每一个候选课程对计算其课程搭配度.具体来说，确定课程cj在包含课程ci的课程对中出现的频繁程度，也就是在已经选择课程ci的条件下选择cj的概率；反之亦然.搭配度计算为

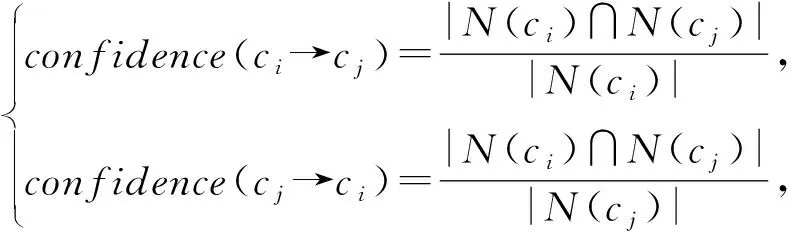
(4)

(5)

根据2个搭配的课程支持度及其置信度构建课程搭配库，将Q(ci,cj)看作2个课程之间的搭配度.

4.3 计算最终推荐度

本文结合4.1节中的用户适合度和4.2节中的课程搭配度，最终得到课程推荐度.通过课程推荐度最终决定给目标用户推荐的课程.

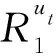
Rec(cj)=w1×P+w2×Q，

(6)

其中，w1和w2分别为用户适合度和课程搭配度的权重系数，取值在[0,1]范围内，且二者之和为1.本文根据总课程推荐度Rec(cj)对候选课程进行排序，选取前k个课程，实现top-k推荐.

本文SMCR模型通过用户适合度和课程搭配度改进了已有方法仅考虑相似度可能导致不当推荐的问题，并且具有较强的可解释性.比如，可以把推荐课程cj的用户适合度和课程搭配度作为推荐的解释.

5 实验与结果分析

本节将在2个数据集CN和MOOC中，通过对比实验来验证本文SMCR课程推荐模型的效果，并对模型参数敏感度进行测试.

本实验的评价指标主要有3个：准确率Precision、召回率Recall和综合指标F1_score.

(7)

(8)

(9)

其中Ru表示课程推荐列表中所推荐的课程样本的个数，Tu表示不同的用户所选择的学习课程样本的个数.

5.1 对比方法

为了验证所提出的方法效果，本文选定了其他5种推荐方法作为基线，即UserCF，ItemCF，LFM，BPR，MPR，简介如下：

1) UserCF[23](user based collaborative filtering).基于用户的协同过滤算法.该算法给目标用户推荐相似用户所选的课程.

2) ItemCF[24](item based collaborative filtering).基于物品的协同过滤算法.该算法给目标用户推荐与其所选课程相似的课程.

3) LFM[25](latent factor model).隐语义模型算法.该算法先对所有的课程进行分类，再根据用户的兴趣分类给用户推荐该分类中的课程.

4) BPR[26](Bayesian personalized ranking).贝叶斯个性化排序算法.根据隐式反馈将给用户推荐的商品按照个性化偏好进行排序.

5) MPR[27](multiple pairwise ranking).多重成对排名算法.该算法通过进一步挖掘具有多个成对排名标准的项目之间的联系，从而放宽了BPR算法中的简单成对偏好假设.

6) SMCR.本文所提结合用户适合度和课程搭配度的课程推荐模型.同时考虑用户对课程的适合度和课程之间的搭配度，并将课程按照推荐度进行排序推荐.

5.2 对比实验结果及分析

本文SMCR及5种基线方法在CN数据集和MOOC数据集上的top-k推荐性能分别如表4和表5所示.其中，k=2.本文也进一步测试了不同k值时的对比结果，如图11和图12所示.

Table 4 Comparison of Experimental Results on CN Dataset表4 CN数据集上的对比实验结果 %

Table 5 Comparison of Experimental Results on MOOC Dataset表5 MOOC数据集上的对比实验结果 %

Fig. 11 Comparison of experimental results under different k on CN dataset图11 CN数据集上不同k值时的对比实验结果

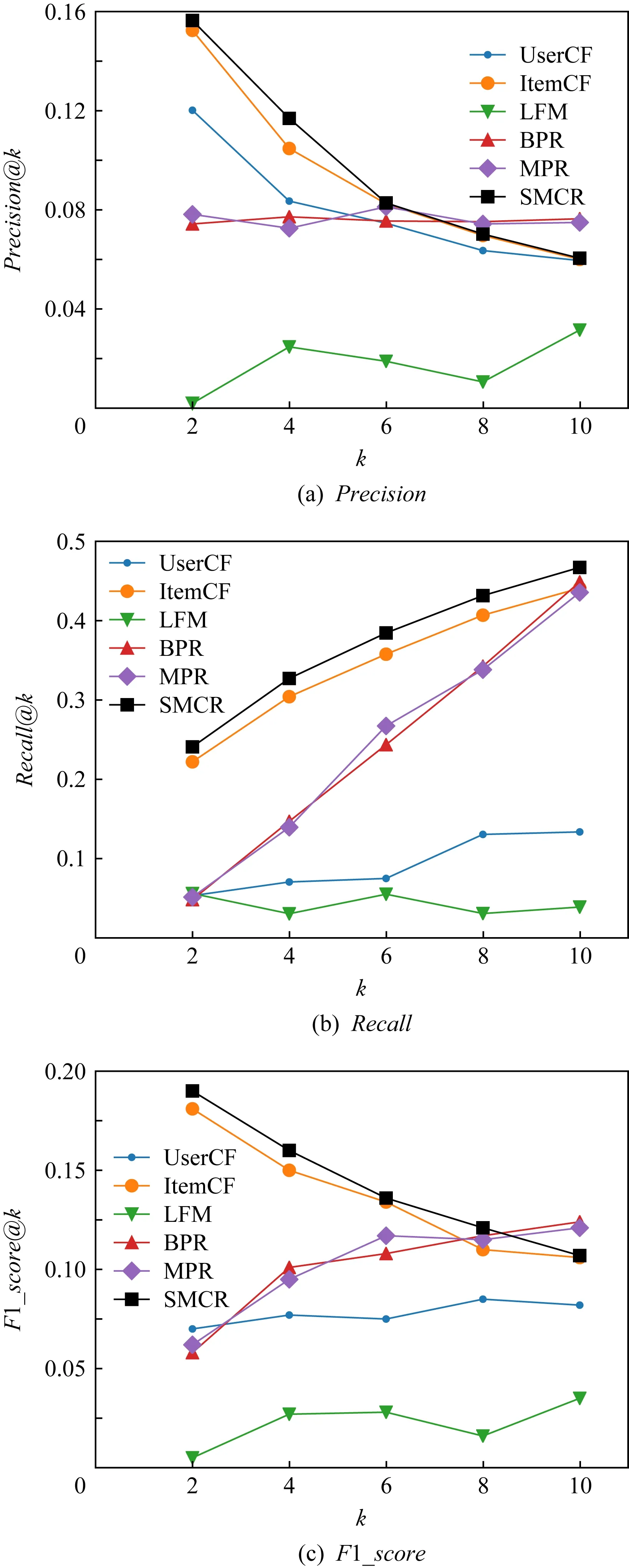
Fig. 12 Comparison of experimental results under different k on MOOC dataset图12 MOOC数据集上不同k值时的对比实验结果

5.2.1 准确性对比

如表4和表5所示，相对5种基线方法，本文SMCR表现最好，ItemCF次之.

表4展示了在CN数据集上进行的对比实验结果.在Precision指标上，SMCR比ItemCF提升了大约2.03%，比BPR提升了大约4.69%，比MPR提升了大约5.17%.在Recall指标上，SMCR比ItemCF提升了大约1.9%，比BPR提升了大约4.41%，比MPR提升了大约4.58%.对表4的分析表明，同时考虑适合度和搭配度能够有效提高推荐准确性.

表5展示了在MOOC数据集上的对比结果.与其他5种基线方法相比，SMCR在指标Precision，Recall，F1_score上的表现效果均最大.例如在指标Precision上，SMCR比ItemCF提升了大约0.4%，在指标Recall上，SMCR比ItemCF提升了大约1.88%.

SMCR的性能相对其他方法更优的原因是其同时考虑了用户和课程之间的适合度以及课程之间的搭配度，而其他方法仅从整体上考虑用户和课程之间的关联关系，如相似历史课程.此外，SMCR在CN数据集上的表现比在MOOC数据集上的表现更好，可能的原因是CN数据集上用户的历史行为记录更多，从而能够帮助更好地挖掘课程之间的搭配关系.

除性能提升之外，本文SMCR相对其他方法更能产生适合用户学习特征的课程推荐.

5.2.2 不同k值的对比

本文课程推荐使用了top-k推荐.在实际的在线学习平台中，每个用户所选课程的数量各不相同.因此实际的top-k推荐列表大小，即k值，与用户所选课程数量有关.

5种基线方法及本文SMCR在CN数据集和MOOC数据集上的推荐性能Precision@k,Recall@k,F1_score@k随k值的变化情况如图11和图12所示，图11中k∈{2,5,8,10,15}，图12中k∈{2,4,6,8,10}.从图11(a)和图12(a)中可以看到，本文中所提出的SMCR的Precision@k值随着k值的增加逐渐降低,当k=10时，该方法Precision趋于稳定.当k<10时，SMCR的推荐准确率相比其他基线方法具有不同程度的提升.当k=2时，图11(a)显示SMCR比ItemCF提升了大约2.03%，图12(a)显示SMCR比ItemCF提升了大约0.40%.

从图11(b)和图12(b)中可以看到，方法推荐结果的召回率Recall@k值会随着推荐个数的增加而增加.这是因为当给用户的课程推荐个数增大时,方法推荐结果会包含更多符合用户偏好的课程.当k=2时，图11(b)显示SMCR在CN数据集上的推荐结果的召回率较对比方法有明显的提升，提升了大约1.90%，图12(b)显示SMCR在MOOC数据集上的召回率比ItemCF提升了大约1.88%.

图11(c)和图12(c)展示了F1_score@k值的变化情况.当k=2时，从图11(c)中可以看到，SMCR较ItemCF提升了大约2.00%；从图12(c)可以看到，SMCR较ItemCF提升了大约0.89%.

综上，当k=2时,SMCR方法的整体推荐效果是最佳的.这说明本文所提出的方法较传统协同过滤方法考虑到了课程之间的关联搭配关系，向目标用户推荐更符合其偏好的课程.从图11来看，当k<4时，SMCR在CN数据集上的准确率小于BPR和MPR，但是召回率大于BPR和MPR，从整体性能来看，其F1_score要大于BPR和MPR，说明与这2个方法相比，SMCR在整体上获得了更好的推荐性能.

5.3 参数敏感度测试

5.3.1k的敏感度测试

本节测试参数k对推荐性能的影响.由于数据集本身具有稀疏性，部分用户只有1个选课记录，会对top-k推荐结果产生影响.因此，需要从原有数据集中选取那些选课记录超过2个的用户并构建新数据集.

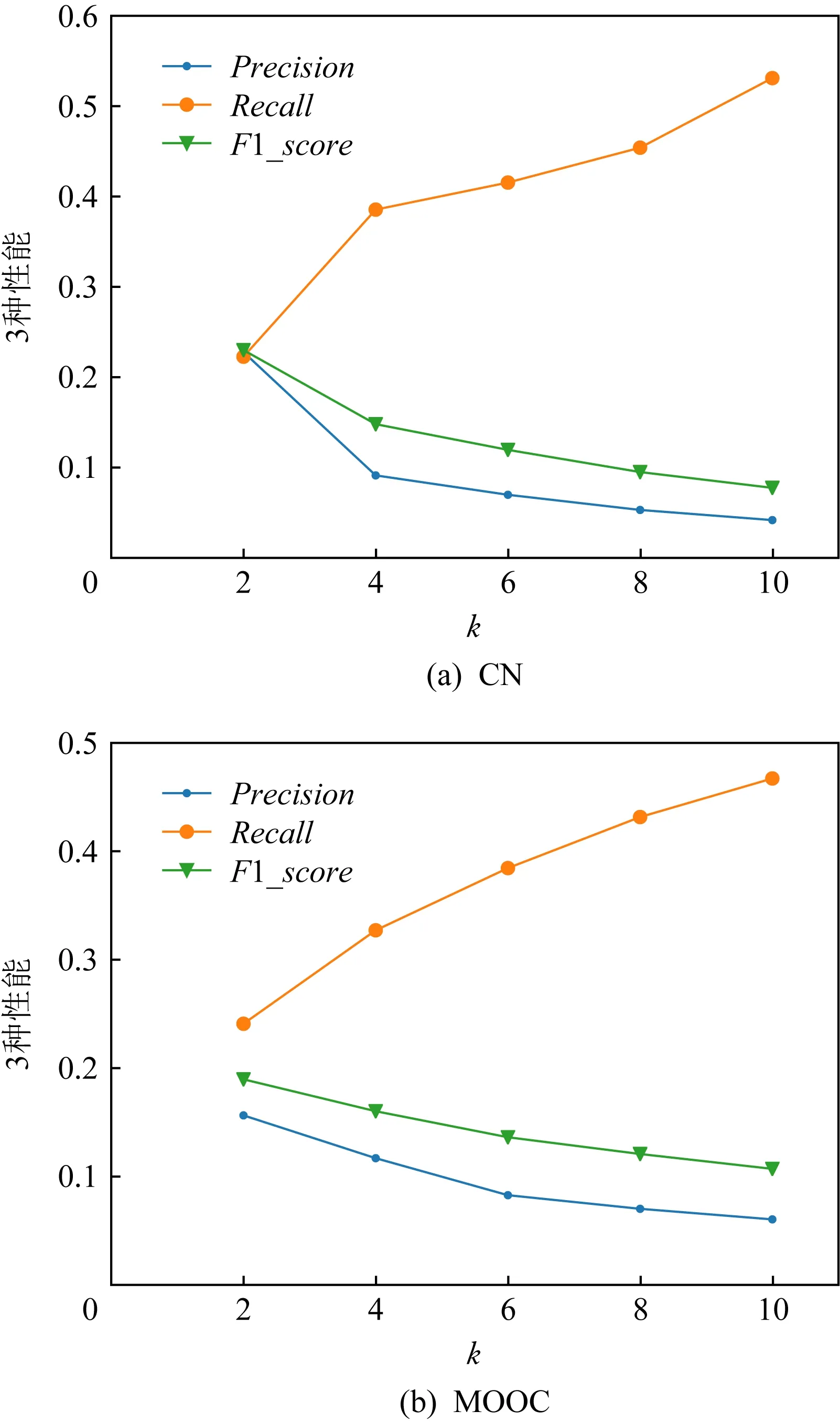
Fig. 13 Performance under different k on two datasets图13 2种数据集上不同k值时的性能

如图13所示，准确率随着k值的增大而减小.这是因为在本文所使用的数据集中，每个用户选择学习的平均课程数为2.5，学习的课程序列较小.但是召回率随着k值的增大而增大，这是因为算法推荐的课程数量越多，就越容易命中真实选课情况.

5.3.2w1和w2的敏感度测试

本文的课程总推荐度是由用户适合度P和课程搭配度Q加权而成的.为了判断这2个量的不同组合对推荐结果的影响，本文在2个数据集CN和MOOC上，对用户适合度和课程搭配度的权重，即w1和w2的不同组合效果进行了实验，结果如图14所示:

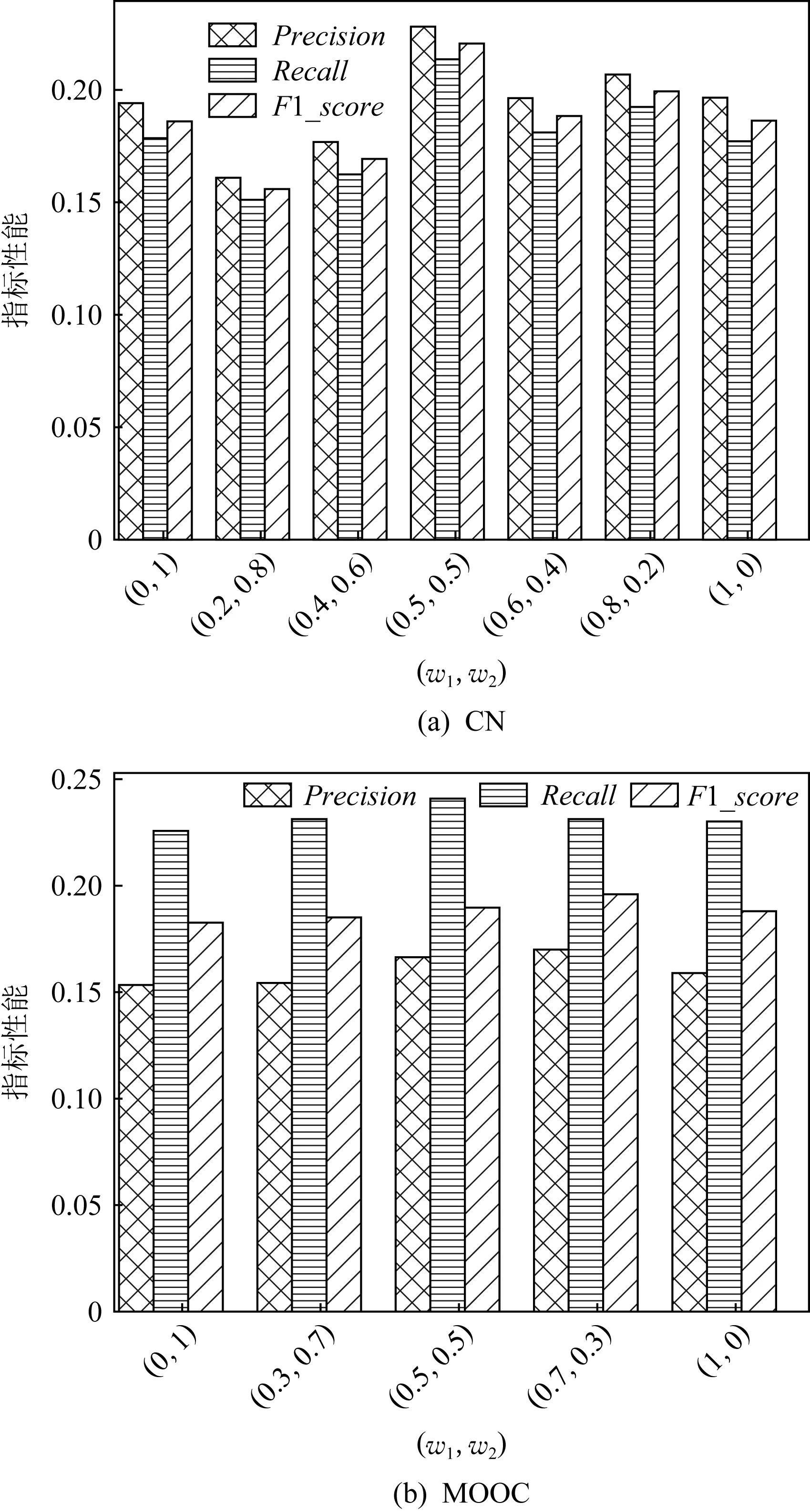
Fig. 14 Performance under different weights of w1 and w2图14 不同权重w1和w2时的性能

从图14(a)中可以看到，在CN数据集上，当w1=0.5,w2=0.5时，SMCR的Precision，Recall，F1_score值均达到最大.说明该数据集中用户适合度和课程搭配度具有基本相同的重要性.

从图14(b)中可以看到，在MOOC数据集上，当w1=0.7,w2=0.3时综合实验效果即F1_score最好.说明该数据集中用户适合度具有更大的重要性.

在最佳权重参数之外，用户适合度和课程推荐度的任意一个权重增大，都会导致准确率或召回率的降低.这说明，针对不同数据集需要深入分析用户适合度和课程推荐度的不同作用，准确地把握二者权重，以便做出更加准确的推荐.

6 总 结

本文通过结合用户适合度和课程搭配度为用户推荐合适的课程.本文提出的SMCR模型能够向用户推荐既适合其学习又与其已学课程可以进行搭配的课程.与其他方法相比，本文全面考虑了用户适合度和课程搭配度2个方面，能够避免仅依赖相似度的传统推荐方法产生的相似课程重复推荐或不当推荐(比如推荐的课程太难)问题.本文使用简单易行的方法达到较好的效果，并具有较强的可解释性.在未来的工作中，我们希望能够更多地挖掘课程之间的内在关联，从上下文信息中提取出关键信息来实现更准确的课程推荐.同时，我们还考虑将知识图谱[28]引入课程推荐中，以达到更好的课程推荐效果.

作者贡献声明：胡园园负责论文撰写与修改、数据分析、方法设计和实验；姜文君负责确定创新点、改进数据、设计实验和全文写作；任德盛负责论文整体思想的讨论与改进；张吉负责论文数据分析和实验的改进.