采用非线性模块的BP神经网络PID水位预测控制

郭 清， 孙 蓉， 徐立芳， 唐 明

（哈尔滨工程大学a.工程训练中心；b.智能科学与工程学院，哈尔滨 150001）

0 引 言

在核电厂运行过程中，蒸汽发生器（Steam Generator，SG）水位需要有效稳定控制在一定的运行值［1-2］，水位控制好坏直接影响核岛的安全运行［3-5］，目前核电厂SG水位普遍采用PID控制［6-10］，针对SG水位控制系统使用传统PI控制效果不佳的问题，本文提出一种基于非线性预测模块的BP神经网络PID控制方法来实现对SG水位的优化控制。

1 解决方案

预测模块起源于工业过程控制，为降低SG水位误差造成不必要的能量损失，构造具有预测功能的非线性BP神经网络PID控制系统，如图1所示。

非线性预测模块的BP神经网络PID控制是将BP神经网络模型作为预测模块，神经网络的训练结果直接传递给PID参数，调整加权系数，结合新的预测值，修正得出预测方向的阈值，得到最优的PID输出值。KP、KI、KD分别为比例、积分、微分系数。

预测算法框架如图2所示，由3部分组成：①常规PID控制器，直接对被控对象进行闭环控制；②BP神经网络NN，根据系统的运行状态，学习改变权系数；③BP神经网络预测模块，实现对未来时刻输出的预测。

2 预测控制算法

2.1 非线性预测模块

设SG水位预测控制系统输出

式中：u（k）为系统的输入信号；ny、nu分别为y和u的阶次；g（·）为与y（k-1）、u（k-1）等有关的非线性函数。

如图3所示，建立一个3层4-4-1型BP神经网络预测模块，计算SG水位控制系统的预测输出值y（k＋1）或∂y（k＋1）/∂u（k）。

以被控对象的输入、输出过程量｛y（k）｝和｛u（k）｝作为BP神经网络模型的默认特征，构建模型的输入层有（ny＋nu＋1）个节点、（q＋1）个隐含层节点和1个输出层节点。输出层神经元的激励函数取线性函数，隐含层神经元的激励函数取Sigmoid函数。

输入层各节点的输出

隐含层节点的输出

式中，ωij为隐含层第i个神经元与输出层第j个神经元之间的连接权值。输出层节点的输出

建立目标误差函数

对于输出层有

式中：η为学习速率（0＜ηR＜1，R＝P.I.D）；α为惯性系数。

对目标误差函数求偏微分有

对于隐含层节点，有

隐含层节点数的大小直接关系到网络的性能［10-11］，由y（k＋1）和u（k）的函数关系，可得

2.2 构造方法步骤

BP神经网络模型是利用非线性可微分函数进行权值训练的多层网络，通过修改各层神经元的权值缩小误差变量［12-15］，建立流程如图4所示。

3 仿真研究

SG水位系统的输入、输出关系

式中：y为SG水位控制系统的输出（最优PID值）；u为SG水位控制系统的输入（水位整定值）；ci为SG水位系统不同位置传感器的整定点。

计算BP神经网络PID控制输出

前向计算得到PID控制的3个可调参数KP（k）、KI（k）和KD（k），输出层激励函数选取g（x）＝［1＋tanh（x）］/2。

计算BP神经网络的输出

仿真某核电厂SG水位控制系统数据［16］，将数据库分成训练数据、测试数据及验证数据3部分。从中选取100对作为训练样本，学习速率ηP＝0.6，ηI＝0.2，ηD＝0.02，惯性系数α＝0.05，加权系数初始值区间为［-0.5，0.5］的随机数。初始输入层至隐含层及隐含层至输出层的权值均设为0.5，隐含层及输出层节点阈值分别设为0.7和0.1，采样时间Ts取1s。构造BP神经网络学习的平方误差

式中：P为输入样本；y′p为经训练后神经网络的输出。训练后的BP神经网络模型获得的数据，见表1，达到预测模块控制拟合精度要求。

表1 训练后BP神经网络模型获取数据

BP神经网络模型输出端y＾（k＋1）输出能够动态跟踪瞬态响应训练数据，如图5所示，训练样本拟合残差ε＝1.3×10-3，说明所设计的BP神经网络模型具有较强的泛化能力。

测试样本可用来检验BP神经网络模型的准确性，选取1 200对数据样本加入BP神经网络模型输入端进行测试，调取部分随机数测试网络模型对给定值的阶跃响应特性，如图6所示，获取的最大测试误差emax＝5.6 mm，满足预测模块的控制精度要求。

应用训练后的网络模型可对SG水位未来数据进行预测，选取30对预测样本，获得的BP神经网络模型输出，见表2，结果显示对于任意选择10个样本，识别正确率为80%，初步验证了BP神经网络模型具有较高的动态特性和自适应调节能力。

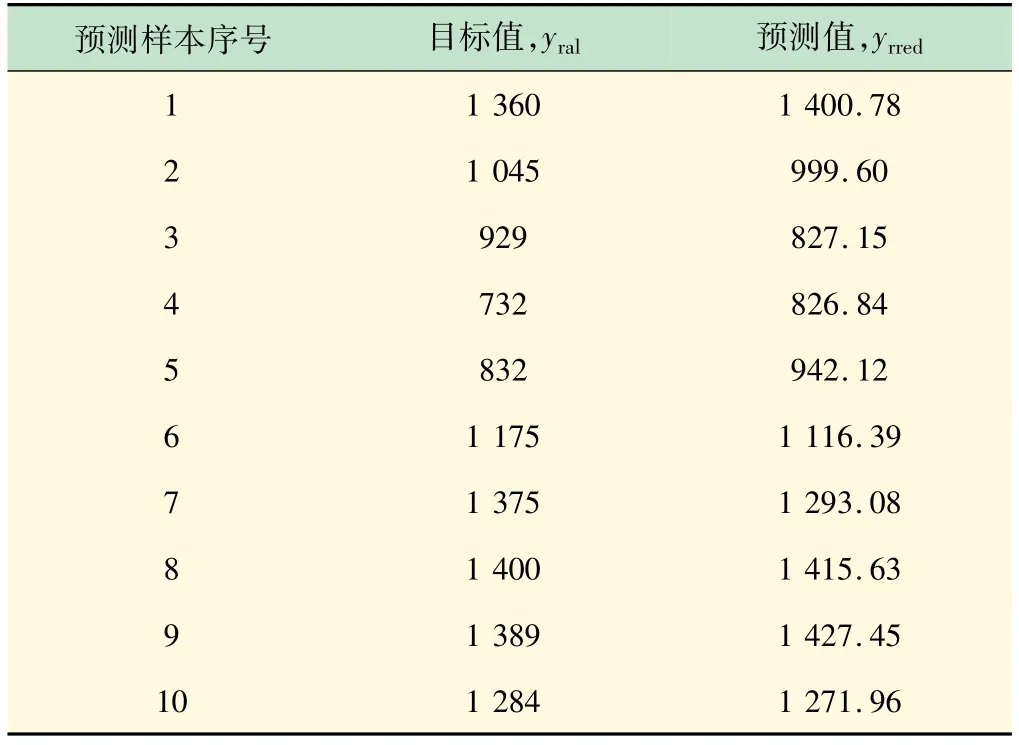
表2 预测样本BP神经网络模型输出

模拟数值在稳态工况下，选择对比3种不同PID控制方法进行验证，见表3，当验证集样本连续满足训练条件即会停止。

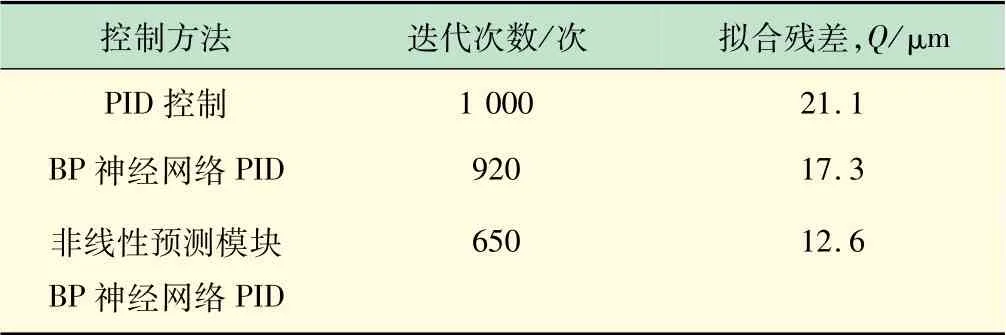
表3 3种SG水位PID控制方法的性能比较

图7显示出非线性预测模块BP神经网络PID控制方法的动态误差最小。

4 试验平台分析

4.1 100%FP（Full Power）平台负荷线性变化试验

系统采用THSA-3型过程控制系统动力装置进行多种工况下的瞬态验证分析试验，如图8所示，动力方案选用电动调节阀支路和变频器支路，智能调节仪数据控制电动调节阀的开量大小及变频器电压的频率。

MCGS组态软件进行现场实时液位传感器及变送器数据的采集与处理，支持对Access、ODBC数据库的访问，见表4。

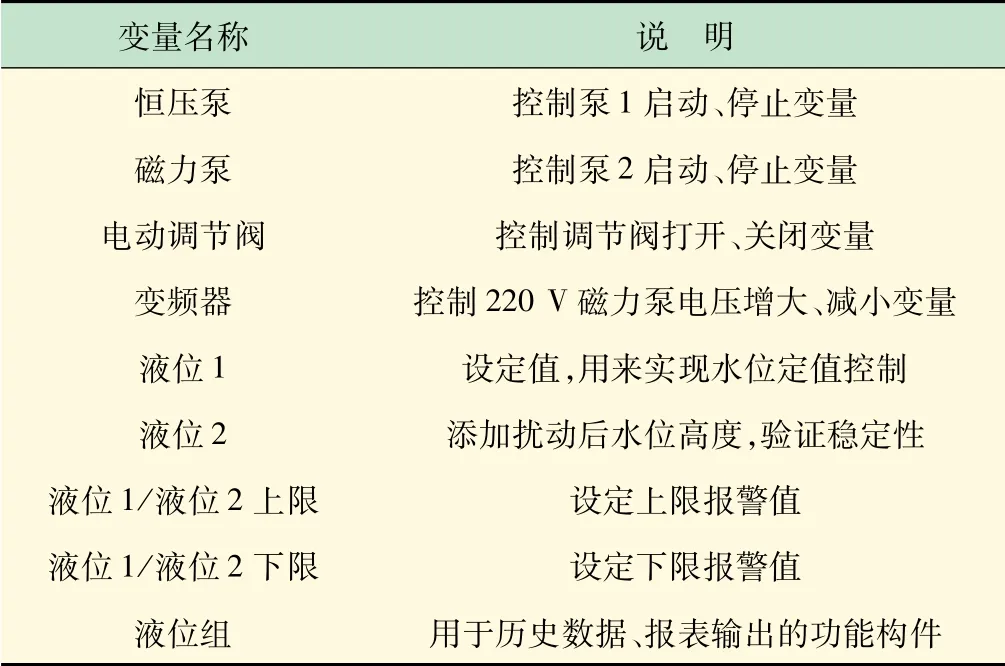
表4 与控制设备相关的主要变量及功能

设维持给水流量与蒸汽流量的平衡，采用正常稳态运行工况，即机组100%FP（满功率），电动调节阀全速进水状态下SG水位动态响应曲线（如图9），水位控制目标值为45%，其中非线性预测模块控制算法的水位变化范围为43%～46%，BP神经网络PID控制范围为40%～45%，PID控制范围为39%～56%，可见，非线性预测模块算法的波动范围最小。

从阶跃响应周期看，非线性预测模块算法控制过渡到稳定时间最短，响应时间不大于800 s，在700 s左右响应就趋于稳定，控制效果明显优于其他两种PID控制方法。

4.2 15%FP和30%FP平台的负荷变化试验

为克服虚假水位产生非最小相位的影响，使SG水位在规定限值之内，分别对负荷为15%和30%时的水位进行仿真控制研究。当负荷为15%时（见图10），变频器输出频率为85%，系统进入稳定时间用时接近650 s；当负荷为30%时（见图11），变频器输出频率为70%，进入稳定时间不超过500 s，表明负荷较小时振荡周期较大，相反增加负荷后振荡周期明显缩短。采用非线性模块BP神经网络PID预测算法时超调量明显小于BP神经网络PID控制及传统PID控制，具有调节速度快和控制精度高的优点。

4.3 50%FP平台的负荷＋多种扰动仿真

为检验预测算法的抗干扰能力，在参数保持一致条件下，选取50%工况下进行干扰模拟实验。当负荷为50%时（见图12），变频器输出频率为50%，在系统运行至680 s时加入10%的蒸汽扰动，预测算法控制系统在750 s回归稳定状态。当系统运行至600 s时（见图13），令水位设定值信号从1.5向下阶跃变化至1，预测算法控制系统在700 s回归稳定状态。图12、13结果表明，在有多重扰动的情况下，相比BP神经网络PID及传统PID控制方法，采用BP神经网络PID预测控制算法使系统响应更快、超调更小，验证所研究的BP神经网络PID预测控制方法具有更佳的动态响应特性和抗干扰力。

综上表明，在存有多种扰动、变工况条件下的瞬态仿真试验研究，非线性预测模块BP神经网络PID控制方法能够有效地缩短SG水位系统的收敛周期，具有更佳的动态响应特性和抗干扰力，实现了非线性预测模块BP神经网络PID控制参数的在线优化整定。

5 结 语

本文开展了多种工况下的SG水位控制预测瞬态试验，对比分析传统PID控制方法和BP神经网络PID两种控制方法，得出结论如下：

（1）预测算法能够参照系统实际运行数据修正预测值的大小和方向，对BP神经网络中的权值和阈值实时同步进行多重优化，能够更精准地跟踪SG水位系统目标整定值，具有移植性和自适应性。

（2）应用于核电领域，可以升级现有的PID控制器，完善各回路的控制系统。

（3）对工业过程控制中的流量、温度、压力以及成分等预测以及其他控制领域都可获得有指导意义的预测结果，具有广阔的使用前景和较大的实用价值。