基于风集合预报的扇区概率拥堵预测
徐子玥,胡明华,张 颖,王 兵,谢 华,丁文浩
(南京航空航天大学民航学院,江苏 南京 211106)
各类对实际运行产生干扰的因素中,天气是最主要的不确定干扰因素,包括恶劣天气和不确定性风[1]。 在航迹预测中风的不确定性直接影响航迹预测的准确性和可靠性,表现为航空器位置、过点时间、燃料消耗的离散[2]。 本文着重考虑不确定性风的影响,量化该不确定性,转化为扇区需求预测的不确定性,以提高ATM 系统的稳定性和可预测性,减少运行成本,提高ATFM 策略的有效性。
如今,量化天气不确定性的趋势是使用集合预报系统(EPS)。 EPS 在ATM 问题中常见应用方法可分为以下两类[2]:
1) 集合预报方法:将集合预报中的概率信息转换为用户相关信息,通过相关信息的统计特征值,量化天气不确定性的大小。 Steiner 等[3]将对流天气的不确定性转化为可用空域容量的减少;Kicinger等[4]采用该方法量化天气不确定性对飞行时间的影响,以衡量天气不确定性在选择最优路线方面的成本;Kim 等[5]将天气不确定性转化为轨迹的不确定性,轨迹集合提供了关于飞行参数的不确定性信息(飞行持续时间和航行燃料成本),将该信息用于轨迹选择;Valenzuela 等[6]考虑风和温度的不确定性,转化为扇区需求的不确定性;Valenzuela 等[6-7]分析了降低轨迹不确定性对扇区需求的影响。
2) 概率转换法:将天气的概率分布函数(PDF)转化为相关信息的概率分布函数。Rivas 等[8],Franco等[9]考虑多航段,将风的PDF 转化为飞行时间和燃料消耗的PDF;Rivas 等[8,10]考虑单航段,将风的PDF转化为燃料消耗的PDF,预测了考虑风预报不确定性的飞行时间及飞行燃油消耗情况。
综上,本文研究了考虑风不确定性的集合轨迹预测方法以及预测轨迹的不确定性分析方法,并在此基础上建立了基于集合轨迹预测进行扇区交通需求集合预测, 以及扇区概率拥挤指标计算的方法, 进而获得风不确定性影响下的轨迹预测集合。基于所预测的扇区概率拥堵,可以实施更为科学有效且具有鲁棒性的流量管理策略。
1 考虑风不确定性的航迹预测
1.1 集合预报
为了表征和量化天气预报固有的不确定性,常采用概率天气预报,其制作方案[2]包括:基于历史误差的方案,预报员的主观解释,确定型预报的统计后处理,集合预报系统(EPS)。 其中,解决ATM 相关问题的趋势是使用EPS。 EPS 通过多次运行初始条件稍微不同的确定性数值天气预报(NWP)/稍微扰动的天气模型[11],时滞[12],多模型[13]等方法构建集合,理想情况下实际天气结果应在集合范围内。
目前运行中常用的EPS 产品包括[5]:
1) 小规模大规模集合天气预报(PEARP)。法国运行全球集合预报模型,由35 个成员组成,每天在0600UTC 和1800UTC 运行。 PEARP 的预报时间范围为中短期(4~5 d),该模型的输出时间间隔为6 h。利用初始条件的奇异向量和集合数据同化,构建34个扰动集合成员。
2)气象局全球和区域集合预测系统(MOGREPS)。由12 个成员组成,每天在0000UTC、0600UTC、1200UTC 和1800UTC 运行。MOGREPS 的预报时间范围为短期(1~2 d),输出时间间隔为3 h。 该模型利用集合变换卡尔曼滤波器,构建11 个扰动集合成员的初始条件。
3) 欧洲中期天气预报中心(ECMWF)。ECMWF的综合预报系统(IFS)由51 个成员组成,每天在0000UTC 和1200UTC 运行。ECMWF 的预报时间范围为中期(15 d),输出时间间隔为6 h。 该模型利用初始条件的扰动(奇异向量技术)、集合数据量同化方法和随机扰动模型的物理参数, 构建50 个扰动集合成员。
4) 超级集合(SUPER)。 结合上述3 种EPS 构建的多模型集合系统。 该模型将PEARP 的35 名成员、MOGREPS 的12 名成员和IFS 的51 名成员混合在一起, 形成98 名成员。 该模型在1800UTC 运行。 SUPER 的预报时间范围42 h,输出时间间隔为6 h(所有组成模型的共同间隔)。
1.2 集合轨迹预测
EPS 应用于航迹预测相关问题的常见方法有两种:
1) 集合预报法(EWF):将集合中的天气成员分别输入确定性航迹预测器(dTP),输出航迹集合。 航迹集合中的成员分别对应于相应的天气成员场景,如图1 所示。

图1 集合预报法示意图Fig.1 Schematic diagram of EWF
EWF 主张从集合每个成员中提取与航空相关的特征,而不是将集合预报提供的丰富信息总结成概率天气描述。 强调每个集合成员的重要性,分析面向集合全体成员,不局限于集合成员的平均值。 不确定性通过集合成员的离散度(最大值-最小值)来表征。
2) 概率转换法(PTM):拟合集合中的天气成员得到概率天气分布,输入概率性航迹预测器(pTP),输出概率航迹,如图2 所示。

图2 概率转换法示意图Fig.2 Schematic diagram of PTM
PTM 允许通过给出的这些随机变量的联合概率密度函数,计算随机变量转换后的联合概率密度函数。
本文拟采用的EWF 是目前应用最广泛的概率预测方法,是一种能够产生一系列未来天气可能性的技术。 相较于PTM,EWF 计算成本更低,更适合于实际应用。
1.3 确定性航迹预测模型
本文采用基于动力学模型中应用最广泛的点质量模型法(PMM)[14-17],构建考虑风不确定性的航迹预测模型,用作EWF 法中的确定性航迹预测器。
1.3.1 构建模型的基本假设
已知航迹的描述有4 个维度: 经度、 纬度、高度、时间。 假设如下。
1) 航空器以恒定空速V=0.84 马赫, 保持恒定高度H=9 800 m 水平飞行。巡航阶段常采用固定马赫数的方式匀速飞行, 该假设固定巡航高度层,避免高度变化导致速度不同,影响马赫数的变化。
2) 航空器处于多航段的巡航飞行阶段,航路点之间视作直线飞行。 该假设忽略航空器的转弯过程,避免转弯过程带来的速度变化,保证航空器以恒定速度飞行。
3) 大气环境:在国际标准大气(ISA)模型基础上叠加EPS 提供的集合预报风数据,将风的不确定性纳入模型考虑范畴。
4) 运动学方程中不考虑横向动力学, 将侧风转化为等效逆风。 本文中假设航空器沿固定航路水平飞行,不存在航迹偏离,忽略风的不确定性对水平航迹的影响,即经过的预定航路及航路点不发生变化。
1.3.2 模型的基本结构
本文着眼于预战术阶段,着重考虑风不确定性的影响,预测得到巡航飞行阶段的航迹集合。 该模型的结构如图3 所示。 输入部分包括:
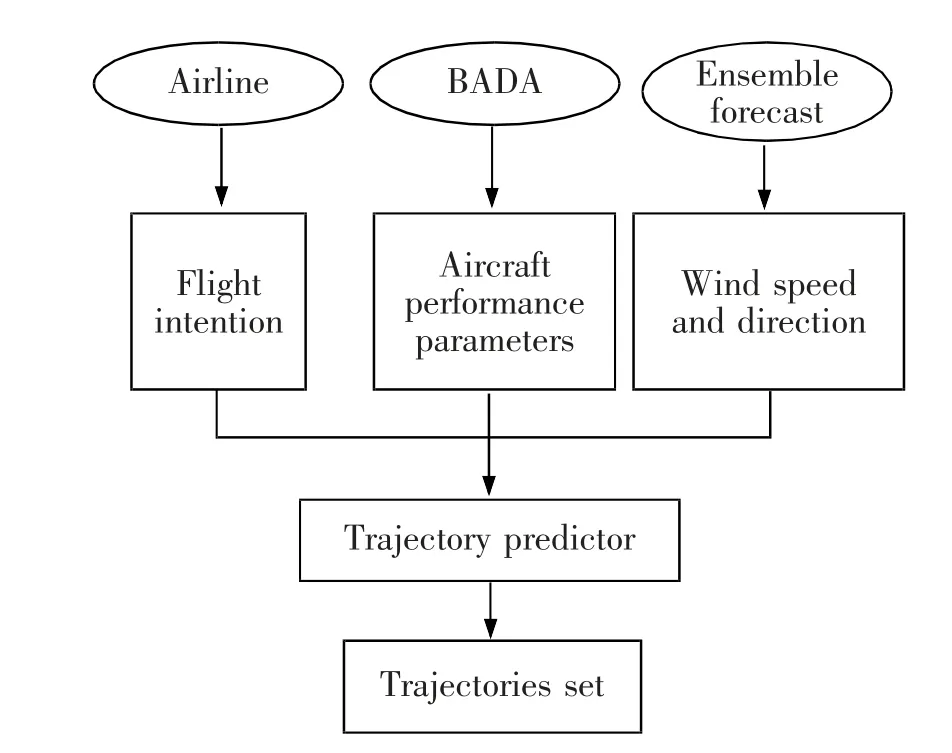
图3 航迹预测模型结构示意图Fig.3 Structure diagram of trajectory prediction model
1) 航空器意图数据。为模型提供简化驾驶员或飞行管理系统操纵航空器的抽象描述。 预战术阶段发生在运行前1~6 d,飞行计划(FPLs)通常尚未可用,主要信息来源是航空器意图(FIs)数据,包含:航班号、出发地和目的地机场、预计起飞时间、航空公司和飞机类型。 在本文中,该数据来源于航空公司运营数据以及导航数据。
2) 航空器性能参数。为模型航空器中动力学方程提供性能方面的参数值。 包含:飞行包线(最大速度、最小速度等),空气动力学(机翼面积和阻力系数),发动机推力和油耗等参数。 本文中,该数据来源于航空器基础资料(BADA)数据库。
3) 气象数据。 为模型提供相关环境信息。 本文考虑风不确定性的影响,风向风速的数据来源于集合预报。
本文仅研究航迹在时间维度上的不确定性——风的不确定性影响航空器的地速,表现为航空器过点时间的不确定性。
模型中航迹以航路点及其相应过点时间的形式来表示,模型输出的航迹集合即为各航路点过点时间的集合列表。
1.3.3 数学模型
已知各网格点上的气象数据,非网格点处航路点上的风值可通过三维线性插值得到(图4)。 具体操作步骤如下:

图4 三维线性插值示意图Fig.4 Schematic diagram of 3D linear interpolation
1) 找到该航路点周围的8 个网格点;
2) 进行高度上的线性插值;
3) 进行纬度上的线性插值;
4) 进行经度上的线性插值。
根据前文假设航空器保持恒定高度飞行,为简化插值过程,航空器在航段内各位置处的风值由航段两端航路点的纬/经向风值线性插值(取决于航空器在航段上的飞行距离)后矢量求和得到。航班i(i=1,2,…,I),集合成员m(m=1,2,…,M)在航段j(j=1,2,…,J)上任一点所受到的纬/经向风uij[m](r)/vij[m](r),r 为航空器在该航段上的飞行距离, 可由航段两端航路点的u 分量和v 分量线性插值得到,数学表达式可写作
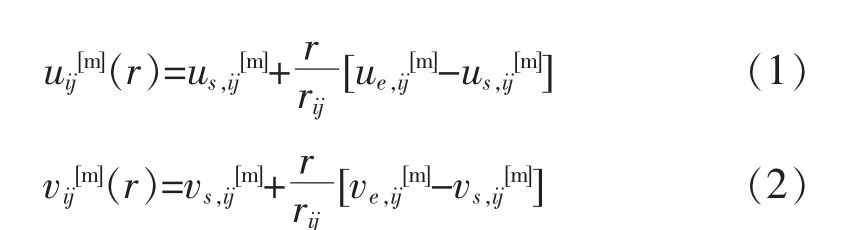
式中:rij为航班i 航段j 的长度,m;us,ij[m]/vs,ij[m](ue,ij[m]/ve,ij[m])分别为航班i 集合成员m 在航段j 的航路起点(终点)的纬度和经度方向的风分量。
该点处的高空风wij[m](r)可由纬度/经度方向风分量求和得到,数学表达式可写作

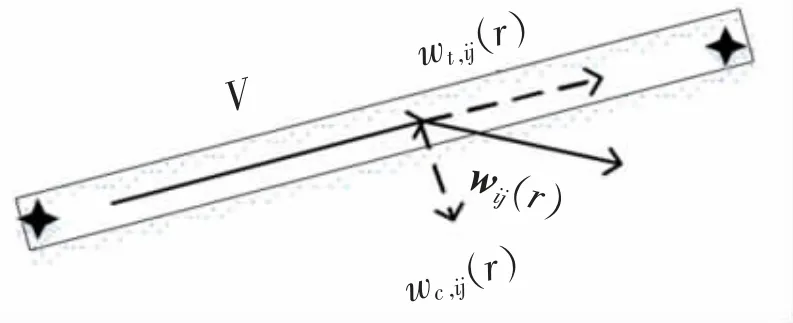
图5 风的矢量三角形示意图Fig.5 Vector triangular diagram of wind
根据假设4,结合风的矢量三角形定理,航班i集合成员m 在航段j 上飞行距离为r 时的地速Vg,ij[m](r)数学表达式为

航班i 集合成员m 经过各航路点p(p=0,1,…,J)的过点时间的数学表达式为

式中:p=0 时该点为航班i 的起时航路点;ti0为航班i 的预计起飞时间。
1.4 轨迹过点时间不确定性分析
1.4.1 定性分析
已知EWF 方法采用集合成员的离散度Spread(即最大值-最小值)来量化不确定性。
1) 风的不确定性:该不确定性具有时空相关性。
①空间相关性:风的不确定性常随地理位置的变化而变化;
②时间相关性:风的不确定性常随预报时间提前量(LAT)的增大而增大,呈正相关关系。
2) 航迹过点时间的不确定性: 表征为预测航迹集合的离散度, 即对于航班航迹上的任一航路点p,该点处航迹过点时间不确定性大小的数学表达式为

根据式(7)中航迹过点时间公式可知,过点时间是以航空器预计起飞时间为起始点,逐个航段推算获得的, 风不确定性的影响沿着航迹不断累积,即航迹的不确定性与航空器到该航路点的飞行距离呈正相关。
1.4.2 定量分析
采用逐步回归法构建多元线性回归模型,分析上述因素与扇区进入时间不确定性之间的定量关系。 已知定性分析中影响航迹不确定性的因素,结合扇区进入时间不确定性问题将其特殊化,则定量分析中, 影响航班的扇区进入时间不确定性的因素,即输入多元线性回归模型的解释变量有
1) 扇区进入点pienter(经过独热编码处理);
2) 预报时间提前量Lienter;
3) 进入扇区时的飞行距离dienter。

逐步回归的基本思想是将变量逐个引入模型,每次引入对因变量影响最显著的解释变量,当原来引入的解释变量由于后面解释变量的引入变得不再显著时,则将其删除。 这是一个反复的过程,直到既没有显著的解释变量选入回归方程,也没有不显著的解释变量从回归方程中剔除为止。 该方法保证将统计上不显著的解释变量剔除,最后保留在模型中的解释变量之间多重共线性不明显,而且对被解释变量有较好的解释贡献。
具体步骤如下:
Step 1 将n 个解释变量xn分别引入模型,同因变量y 构建n 个一元回归模型。 计算各解释变量相应的F 检验统计量的值。 当其最大值超过给定显著水平对应的临界值时,对应的解释变量引入选入变量指标集合。
Step 2 将剩余n-1 个解释变量分别与选入变量指标一起引入模型,同因变量y 构建n-1 个二元回归模型,计算得到相应的n-1 个F 检验统计量的值, 当其最大值超过给定显著水平对应的临界值时,将新的解释变量引入选入变量指标集合,否则终止引入过程。
Step 3 重复步骤2,构建n-h(h≤n)个(h+1)元回归模型, 直到F 检验统计量的最大值小于给定显著水平对应的临界值或h=n 时, 终止引入过程。
2 扇区交通需求及扇区拥堵预测
2.1 扇区交通需求集合预测及分析
将第1 节得到的航迹集合,转化为扇区需求集合,并根据扇区需求集合的特征统计量,分析考虑风不确定性的扇区需求。
本文将扇区需求定义为:选定时间段Pk内进入扇区的航空器数量。 Pk的数学表达式如下

对所预测的扇区需求集合中的各预测值进行统计分析,计算如下统计指标值:最大值(Max)、最小值(Min)、平均值(Avg)、离散度(Spread),计算式如下

2.2 扇区拥堵指标
扇区拥堵定义为:某时间段内,扇区需求超过扇区声明容量(Capacity)。 本文中扇区声明容量假设为定值,扇区需求存在不确定性,通过匹配确定性容量和不确定性需求判断扇区拥堵。
由于ATFM 措施的严重性取决于扇区拥堵的可能性及严重性,本文定义扇区拥堵指标,扇区拥堵概率,预期扇区容量缺失值如下
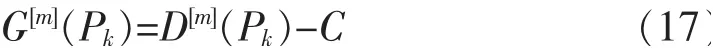
式中:G[m](Pk)为选定时间段Pk内,集合成员m 的扇区容量缺失值,定义为扇区需求与扇区声明容量的差值,为正值时表示扇区拥堵;C 为扇区容量。
引入单位阶跃函数的概念用于指示扇区是否拥堵,数学表达式为

3 实例计算
3.1 数据
1) 扇区:本文选取ZUUUAR04 扇区作为对象,分析扇区概率需求, 已知该扇区的声明容量为28架/h,7 架/15 min。
2) 航班:北京时间2019 年6 月8 日00:00—24:00 途经扇区ZUUUAR04 的航班,共计429 架。扇区 进 入 点 有:CDX (229 架/53.4%)、GYN (1 架/0.2%)、OMBON(192 架/44.8%)、P247(7 架/1.6%)。
3) 集合天气预报:ECMWF 在UTC 时间2019年6 月7 日00:00 的预报。
3.2 确定性航迹与不确定性航迹集合的对比
本文采用确定性模型进行考虑风预报不确定性的航迹预测,风预报的不确定性通过EWF 方法来量化。 根据前文所述ECMWF 的集合构建方法,可知风集合预报中成员0 为初始天气预报, 成员1~50 为扰动成员。 现将成员0 得到的确定性航迹, 与考虑风预报不确定性得到的不确定性航迹(成员0~50 得到的确定性航迹集合) 对比如图6所示。

图6 确定性航迹与不确定性航迹集合Fig.6 Determined trajectory vs undetermined trajectory set
由图6 可知, 横坐标表示该航迹的航路点编号,纵坐标表示该航迹的预计过点时间。 红色实线表示集合成员0 预测得到的确定性过点时间,紫色/蓝色直线分别代表集合成员预测得到的最小/最大过点时间,紫色蓝色直线范围内即为航迹的可能过点时间区间,相较于确定性过点时间,增加了预测航迹的鲁棒性。
3.3 不确定性分析
3.3.1 轨迹过点时间不确定性分析
1) 定性分析。绘制各航班进入扇区时的飞行距离、预报时间提前量与扇区进入时间离散度的散点图,分别如图7,图8 所示。 蓝色实心点分别为各航班进入扇区时的飞行距离、LAT 及其相应的进入扇区时间的离散度, 红色实线是散点拟合出的趋势线。 可以看出扇区进入时间离散度与航班进入扇区时的飞行距离、预报时间提前量成正相关关系。

图7 扇区进入时间不确定性与飞行距离关系图Fig.7 Dispersion of the entry time vs flight distance to the entry point

图8 扇区进入时间不确定性与LAT 关系图Fig.8 Dispersion of the entry time vs LAT
2) 定量分析。 于SPSS 平台上,基于逐步回归分析法构建多元线性回归模型,分析各因素对扇区进入时间离散度的影响情况。
本文用于判定是否引入该解释变量的临界值设为0.1,表示当候选变量中最大F 值的P 值小于或等于0.1 时,引入相关变量。在引入方程的变量中,最小F 值的P 值大于或等于0.1 时,则剔除该变量。
逐步回归过程中每一步骤输入/除去解释变量,构建多元线性回归模型的结果摘要如表1 所示。

表1 模型摘要Tab.1 Model summary
经过逐步回归, 模型3 中修正后的R2=0.874,大于0.8,表示模型拟合效果较好;F 值为28.022,伴随回归的显著性检验0.000<0.05, 说明逐步回归法调整后的方程联合显著性检验通过。 模型3 拟合得到的多元线性回归方程为
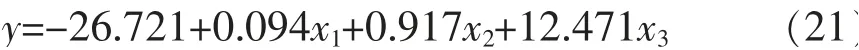
式中:y 为航班进入扇区时间的离散度;x1为航班进入扇区时的飞行距离dienter;x2为航班进入扇区时的预报提前时间Lienter;x3为航班进入扇区时的航路点OMBON。
3.3.2 扇区需求不确定性分析
所预测扇区需求的不确定性特征影响扇区概率拥堵的计算,本节重点分析不同的统计时间段周期长度T 下的扇区需求的不确定性特征。
当选定时间段周期T=60 min,扇区进入计数的统计特征量(Min、Max、Avg)如图9 所示。

图9 T=60 min 时各时间段内扇区需求Fig.9 Sector demand for T=60 min
扇区进入计数的平均值在22:00—23:00 处取最大值,考虑到扇区声明容量为28 架/h(图中用红线表示), 可知在21:00—22:00 和22:00—23:00 这两个时间段内,累积持续时间120 min,扇区需求大于扇区声明容量,存在拥堵的可能性。
各选定时间段内, 扇区进入计数的不确定性(离散度)如图10 所示。

图10 T=60 min 时各时间段内扇区需求离散度Fig.10 Dispersion of the sector demand for T=60 min
离散度在22:00—23:00 时间段处取最大值,为3 架。 相较于扇区的声明容量28 架/h,大约占比11%。
当选定时间段周期时,扇区进入计数的统计特征量(Min、Max、Avg)如图11 所示。

图11 T=15 min 时各时间段内扇区需求Fig.11 Sector demand for T=15 min
扇区声明容量随选定时间段周期成比例减小为7 架/15 min,如图12 所示,共计11 个时间段内,累积持续时间165 min, 扇区进入计数大于扇区声明容量,存在拥堵的可能性。
各选定时间段内, 扇区进入计数的不确定性(离散度) 如图12 所示。 离散度在02:45—3:00、22:15—22:30、22:30—22:45、23:00—23:15 这4 个时间段处取最大值,为3 架。

图12 T=15 min 时各时间段内扇区需求离散度Fig.12 Dispersion of the sector demand for T=15 min
比较上述两种情况,选定时间段周期T 减小时,扇区进入计数成比例缩小,但离散度变化不大,即扇区需求成比例缩小, 需求不确定性的重要性显著提高。 与此同时,根据扇区平均需求计算的超出容量事件的发生频率提高,累积超出容量持续时间变长。
3.4 扇区概率拥堵指标分析
分别计算得出选定时间段周期T=60,15 min时,各时间段内扇区拥堵概率及其相应的预期容量缺失值,并将其可视化,如图13 所示。

图13 各时间段内扇区拥堵概率及预期容量缺失值Fig.13 Sector congestion probability and expected capacity deficit values for each time period
图13 中, 蓝色柱状图表示该时间段内扇区拥堵概率,红色折线图表示该时间段内预期的扇区容量缺失值。
从图13 可以看出,当T=60 min 时,在22:00—23:00 时间段内; 当T=15 min 时, 在23:00—23:15时间段内,扇区拥堵概率最大,同时扇区容量缺失值最大,扇区概率拥堵风险最大,ATFCM 策略最严格。
4 结论
1) 研究了考虑风预报不确定性的集合轨迹预测方法,并分析了轨迹预测的不确定性随预报时间提前量以及飞行距离的变化趋势。 实例验证可知,轨迹预测的不确定性与预报时间提前量、飞行距离均成正相关关系。
2) 研究了航班过点时间预测不确定性量化方法, 基于逐步回归法建立了多元线性回归方程,经检验该模型具有显著性,能量化各个因素对航迹过点时间预测不确定性的贡献度。
3) 研究了基于集合轨迹预测进行扇区交通需求集合预测以及扇区概率拥堵指标计算的方法,并分析了扇区概率拥堵相关的两个指标随不同统计时间段粒度的变化特征。 实例计算结果表明:当选定时间段周期减小时,扇区拥堵的概率增大,扇区拥堵概率达到阈值的累积持续时间增大。

