差分隐私模糊聚类位置保护方法
林 静,胡德敏,王揆豪
(上海理工大学 光电信息与计算机工程学院,上海 200093)
在信息化时代,移动终端的位置服务广为人知,签到、导航、线路跟踪等功能也存在于大量软件中。为了增加搜索功能以便最大限度地提高效益,LBS(Location Based Service)[1]服务提供商收集大量用户定位信息,形成用户轨迹数据,并对这些数据进行分析优化,从而给出兴趣点推荐及位置共享服务等。基于位置的数据发布虽然增加了日常生活的便捷性,但也增加了个人隐私信息被泄露的风险[2]。
目前国内外应用在LBS背景下的位置隐私保护方法可分为4类:抑制法(Suppression)、加密法(Cryptography)、泛化法(Generalization)和扰动法(Confusion)。抑制法[3]是一种基于先验知识,通过抑制敏感背景信息来保护用户隐私的方法。但在需要删除太多数据的情况下,这种方法会丢失大量数据,导致数据查询服务质量低下。数据加密法[4]采用某种加密协议来实现身份和位置的保护,但是其实现过程需要较大的计算量,且匿名过程延时较长,实际应用效果不佳。泛化法[5]通过将数据点或数据轨迹由点到面进行转换,以此来保护用户位置隐私。由于泛化法需要加入很多辅助数据,导致算法运行效率降低且数据冗余过多。为了给真实数据增加噪点并扰乱其真实性,一般采用数据扰动法[6]。该方法用伪造的位置数据来替代原有数据集中真实的位置数据,例如文献[7]提出的Virtual Avatar轨迹隐私保护方案,就是用扰动的数据点对真实的位置数据进行干扰,但是添加过多假数据会导致查询请求结果不可靠。
差分隐私是在数据扰动法的基础上提出的,主要是通过给位置点加噪声扰动来保护真实的位置信息,具有严格的推理过程和数学证明,常被应用于位置隐私保护中。目前对于位置点加噪主要分为两种方式:一是直接对此位置点加上满足差分隐私的噪声,但该方法会造成隐私预算过大、冗余过多,影响数据的真实性;二是对数据转化后再添加噪声,又可进一步分为网格划分法和聚类法。网格划分法是自顶向下逐步细分网格,寻找最优划分是算法的关键,但对于分布不均的数据集来说,网格大小相同,对应每个网格密度值的差别过大,加入噪声后,扰动位置点并不能有效代表真实位置点。
基于聚类的数据加噪是近些年来相关工作中主流的研究方法,本文通过聚类与差分隐私相结合的方法来研究位置隐私保护。文献[8]通过将拉普拉斯噪声添加到实际的位置来保护用户隐私,但这并不适用于移动环境,噪声的叠加会影响数据的可用性以及查询结果的真实性。文献[9]将差分隐私与K-means算法相结合,添加拉普拉斯噪声到该组的中心点,在获得干扰数据点之前,通过合并位置点产生泛化效应,从而达到保护位置隐私的效果。然而,该方法对于初始中心点和初始值k的设置较为敏感,对k值的选取会对结果产生一定的影响。文献[10]提出了基于差分隐私的混合位置保护方法,该方法将随机噪声添加到离散点,使用K-means算法将噪声添加到非离散点泛化后的中心点,但对离散点直接添加噪声会导致噪音数据过多,增大误差;对于非离散点使用K-means算法聚类,选取不同初始聚类中心也会对结果产生较大影响。若存在异常点,会导致均值偏离,从而降低数据的可用性。
常见的差分隐私聚类位置保护方法对离散点敏感,且会盲目选择初始值,导致结果不理想。此外,隐私叠加、隐私预算消耗过大也会降低数据的可用性。为了在满足差分隐私的条件下,最大化查询结果的精确性并提高算法效率,本文设计提出了一种差分隐私模糊聚类位置保护方法(Differential Privacy Kernel Fuzzy Clustering Location Protection Method,DPK-F),将差分隐私与模糊C均值聚类算法(Fuzzy C-Means Clustering,FCM)相结合,同时使用BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)算法确定初始值,使得每一个输入数据以隶属程度来选择类别。通过高斯核函数将数据点映射到特征空间,降低计算负载。随后,选取最终聚类集合的质心点,加入满足差分隐私的拉普拉斯噪声,得到每个位置集合的扰动位置,并使用扰动位置进行查询。实验结果表明,该方法可以在保护用户的位置隐私前提下,降低查询误差,提升算法效率。
1 差分隐私模糊聚类位置保护方法
1.1 基本定义
定义1差分隐私。给定一个算法K,若对于任意的数据集T1和T2,T1和T2里面只相差一个记录,δ为一个比较小的常数,输出S∈Range(K)满足
Pr{K(T1)∈S}≤eε×Pr{K[T2]∈S}+δ
(1)
则该算法符合ε-差分隐私[11]。
定义2全局敏感度。假设函数f:D→Rd,D是一个数据集。对于任意的两个临近数据集D和D′,有
GSf=maxD,D′‖f(D)-f(D′)‖
(2)
其中,GSf为函数f的全局敏感度[12];‖·‖表示曼哈顿距离,定义如式(3)所示。
‖x‖=|x1|+|x2|+…+|xn|
(3)
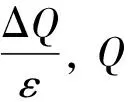
ΔQ=maxD,D′‖D-D′‖=1‖f(D)-f(D′)‖
(4)
概率密度分布如式(5)所示,λ为偏移量。
(5)
定义4欧氏距离。n维空间中两点间的真实距离,或一个矢量的长度[14]为欧氏距离,如下式所示。
(6)
定义5误差平方和。样本x与样本总平均值的偏差平方和是衡量样本离散程度的重要指标,如式(7)[15]所示。
(7)
1.2 相关技术
1.2.1 隶属函数
隶属函数是衡量一个对象x属于某个集合A的程度的函数,通常被记做μA(x)。它的范围就是属于集合A的所有值,取值范围为[0,1]。当值为1时,代表x完全属于集合A;当值为0时,就表示x完全不属于该集合。因此,一个对象的隶属函数就定义了一个模糊的集合。对于对象x1,x2,…,xn,模糊集合A可表示成式(8)。
A={(μA(xi),xi)|xi∈x}
(8)
将每个聚类结果看作是一个模糊集合,每个数据点所对应集合的隶属度在[0,1]区间内。
1.2.2 核函数模糊C均值聚类
基于高斯核函数改进的模糊C均值聚类算法(Kernel Fuzzy C-Means Clustering,KFCM)是指通过一个核函数将原始空间中的点直接映射至一个特征空间中。考虑到无法用一个线性函数对原始空间中的点进行划分,于是将其经过变换放到一个高维空间中,并在这个高维空间中寻找到一个线性函数与之相对应,使之更容易对原始数据进行划分[16]。本文选取基于核函数的模糊聚类算法,在提升算法精度的同时,使扰动位置用户查询可以更好地代表真实用户的需求,缩短了查询时间。
高斯核函数模糊聚类算法中,设X∈Rs,定义从X到特征空间H的映射为
φ:X→H:φ(x)=y
(9)
(10)

(11)
式中,K(vi,xj)是高斯径向基函数[18],其形式如式(12)所示。
(12)
利用拉格朗日的极值必要条件,求出聚类中心V和隶属度矩阵U。
(13)
(14)
算法步骤如下:
步骤1FCM算法初始化隶属度矩阵U;
步骤2用式(13)计算U(k+1);
步骤3根据式(14)计算V(k+1),令k=k+1;
步骤4重复步骤2和步骤3,直到满足如式(15)所示的条件,或存在i(1≤i≤c),使得式(16)成立,则可终止。
‖U(k)-U(k-1)‖<ε
(15)
(16)
1.3 确定聚类初始点和聚类数
对位置点进行隐私保护时,需要在不暴露用户真实位置的前提下,得到尽可能准确的查询结果。本文先对用户位置点聚类,然后选取聚类后具有代表性的点,加入满足差分隐私的拉普拉斯噪声得到扰动位置点,并使用扰动位置代替真实位置查询。但聚类算法普遍存在对初始点敏感且容易陷入局部最优解的问题。为了让初始化选取更加科学,实现更准确的聚类效果,本文采取BIRCH算法初步分类数据。
BIRCH利用层次方法的平衡迭代规约和聚类,只需要单遍扫描数据集就可以开始进行聚类。该算法使用了一个类似B+树的树结构来协助迅速聚类。该树结构与平衡B+树相似,故将其称为聚类特征树。这棵树的每一个节点均包含若干个聚类特征,树中的每一个节点都可以对应一个簇,子节点所对应的簇也就是父节点对应簇的子簇。BIRCH算法流程如图1所示。

图1 BIRCH算法流程图
1.4 DPK-F算法
本文采用扰动位置代替真实位置进行LBS查询,在查询过程中需要对用户真实位置进行保护。通常采用聚类的方法先将真实位置点聚类,选出具有代表的点进行位置查询,若攻击者有足够多的背景知识,就会轻易推断出用户的隐私信息。所以本文将差分隐私与核函数模糊聚类相结合,提出一种差分隐私模糊聚类位置保护方法(DPK-F)。此方法不仅能够保护有效用户位置隐私,也提高了算法的效率。算法模型步骤如图2所示。
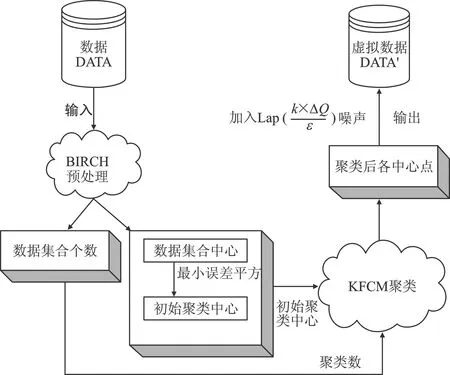
图2 DPK-F模型步骤
DPK-F算法分为3个环节:
(1)采用BIRCH算法将数据集初始化,得到聚类数,判断初始点;
(2)运行KFCM算法对数据集进行聚类;
(3)取簇质心点,加入符合差分隐私的拉普拉斯噪声。
DPK-F算法的具体步骤如下:
输入:数据对象集D。
输出:符合差分隐私的结果集合Dres。
步骤1在数据对象集D上运行算法BIRCH,算法参数都取默认值,得到聚类个数k和各集合Ck;
步骤2计算Ck对应集合的误差平方和,取最小误差平方和φmin所对应的簇中心点d作为聚类初始点;
d=dminφk
(17)
步骤3设定径向基函数的参数σ、聚类个数k、模糊指数m(一般取[1.5,2.5])以及收敛精度ε(此处取0.000 01),令迭代次数为0,用FCM算法初始化隶属度矩阵U,并运行KFCM算法聚类径向基函数
(18)
运行目标函数
(19)
其中,聚类中心V、隶属度矩阵U分别如下所示
(20)
(21)
当‖U(k)-U(k-1)‖<ε或存在i(1≤i≤c)使得
(22)
此时,迭代终止;
步骤4得到最优聚类集D′;

M(Ci)=f(Ci)+Y,i=1,…,k
(23)
(24)
步骤6输出差分隐私保护的扰动后数据集Dres。
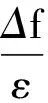
证明设数据集D通过高斯核函数模糊聚类得到若干个不同聚类。则D=C1∪C2∪C3∪…∪Cn,D′=C′1∪C′2∪C′3∪…∪C′n,由式(1)和式(2)可知
(25)
(26)
由式(25)除以式(26)得
(27)
只需,|f(C1)-f(C′1)|≤max(C1,C′1),|f(C1)-f(C′1)|=Δf1,即满足(ε1,δ)-差分隐私。
同理,由并行组合定理可知,算法DPK-F满足差分隐私要求。
算法流程如图3所示。
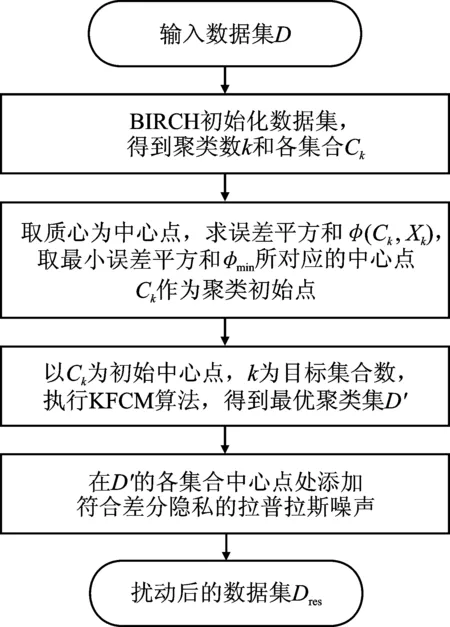
图3 DPK-F算法流程图
2 实验与分析
本文基于用户获取LBS服务的响应时间以及查询结果的准确性和误差等方面来衡量隐私保护效果。本文分别在Gowalla位置签到数据集以及虚拟用户位置数据集(Data)上进行实验。其中,Gowalla位置签到数据集包含了用户ID、经纬度、签到地点ID等重要信息。通过提取用户签到经纬度作为位置点数据,并以地点ID作为请求的查询位置来进行实验分析。通过与经典差分隐私K-means保护算法和文献[11]提出的混合K-means保护算法进行指标对比来验证本文所用方法的性能。
本文使用Python编程语言进行仿真实验,使用Thomas Brinkhoff路网数模拟器生成1 000个模拟数据,将其组成一组模拟用户位置查询数据集。单机环境为Inter(R)Core(TM)i7 CPU 3.7 GHz,8 GB内存,Windows 10 64位操作系统。
2.1 查询准确度分析
实验查询结果的准确性使用聚类评价指标轮廓系数、准确率来分析,本文采用差分隐私与聚类方法结合,目的是为了聚类真实位置点,选取足够代表用户查询位置的扰动位置点进行查询。因此,聚类效果可以有效反应出查询的准确性。实验分别对比了DPK-means、混合DPK-means算法在Iris、Wine、Gowalla和模拟数据集Data上的效果。
通过图4可以看出,与其他经典算法相比,本文提出的DPK-F算法在Iris、Wine、Gowalla和模拟数据集Data上的轮廓系数更接近于1。这表明在相同隐私预算条件下,本文所提方法的聚类性能更好,虚拟值能更好地代表真实值,准确度更高。
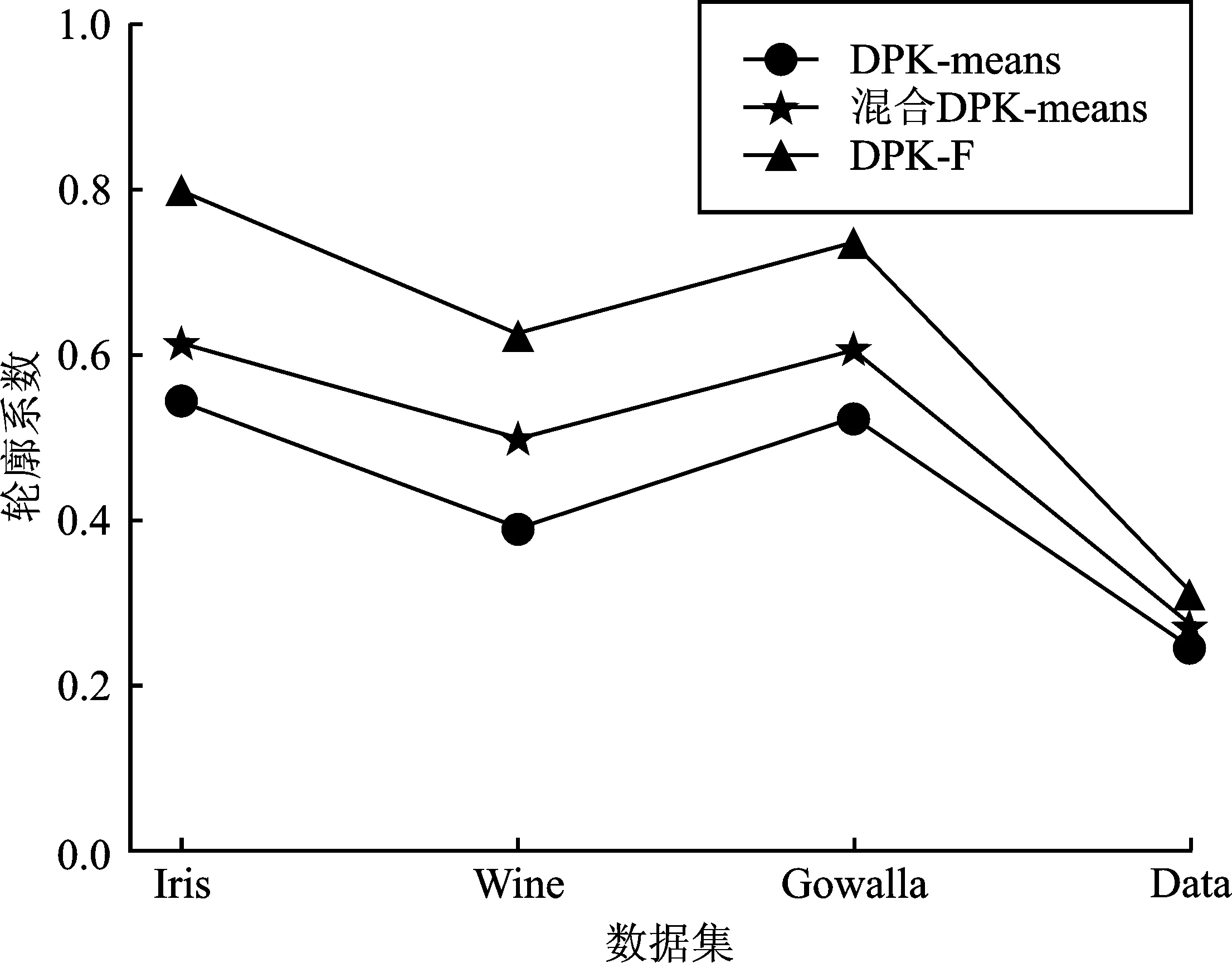
图4 轮廓系数对比
通过图5可以看出,隐私预算ε越接近1,准确率越高。在相同隐私预算ε下,与其他算法相比,本文提出的DPK-F算法在Iris、Wine、Gowalla和模拟数据集Data上的聚类准确率大于90%,优于其他算法。实验结果表明DPK-F算法分类结果更精确,查询准确性更高。
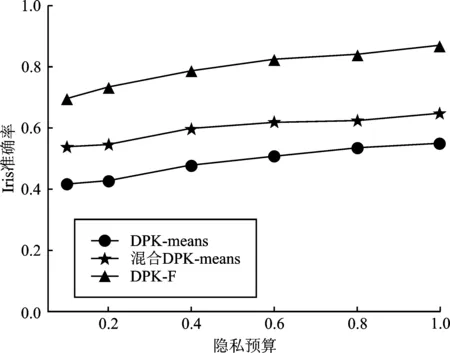
(a)
2.2 数据可用性分析
本文采用相对误差来衡量实验的数据可用性,其计算式为
(28)
式中,A(s)表示真实查询结果;QM(s)代表经过位置隐私保护算法后运行的查询结果;p=0.001×|D|;D为数据集样本数。相对误差可有效反映出算法的查询误差,避免由于匿名区域大小差别过大,或噪声添加差别过大而导致的查询精度下降问题。相对误差越小,表示查询结果越接近真实结果,数据可用性越好;反之,相对误差越大,表明查询结果越偏离真实结果,数据可用性低。实验分别对比了DPK-means、混合DPK-means算法在Gowalla和虚拟数据集Data上的效果。
图6给出了DPK-F算法与DPK-means、混合DPK-means在不同数据集中改变隐私预算时的相对误差变化情况。
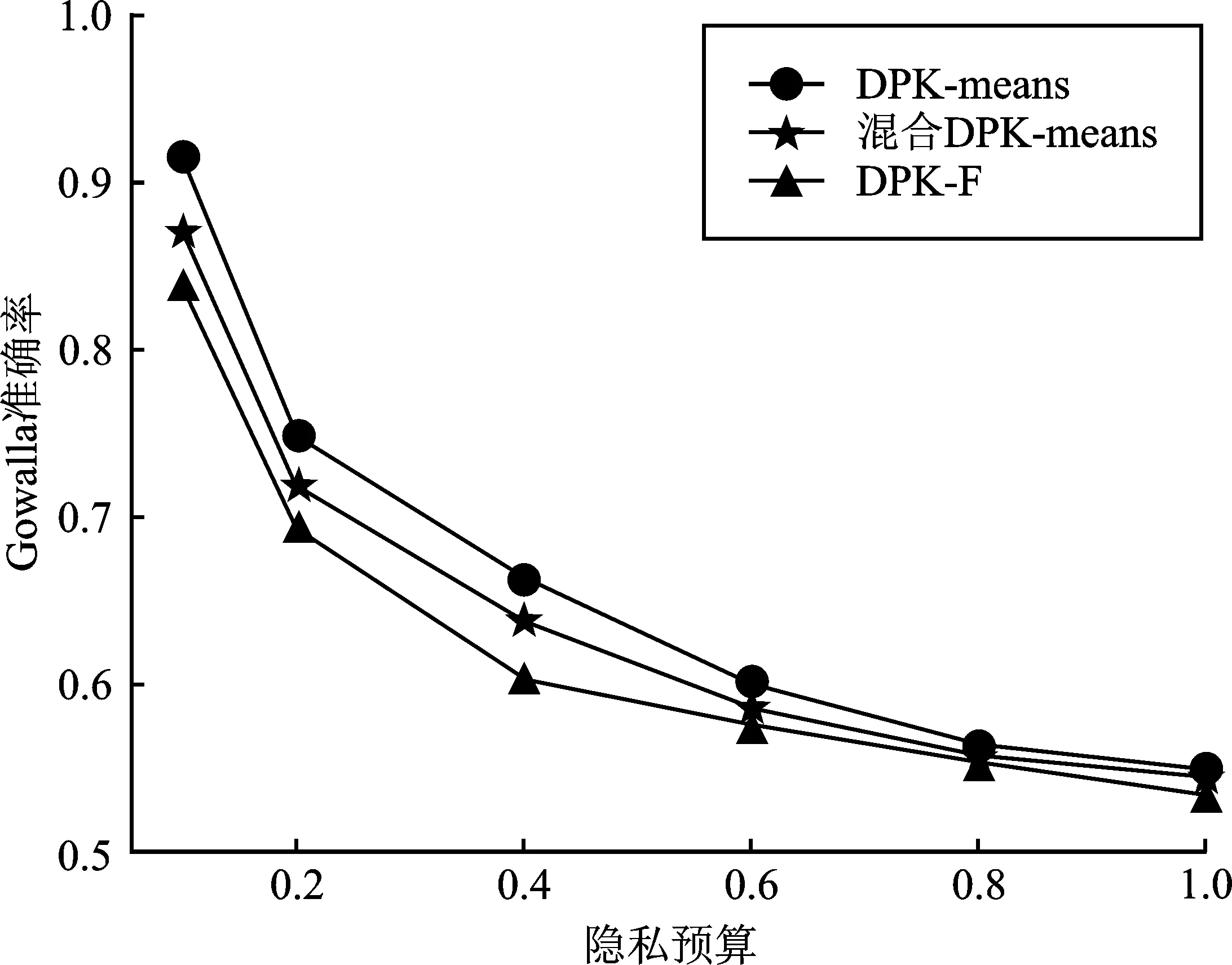
(a)
从图6可以看出,实验误差随隐私预算ε的增大而减小。在同一隐私预算下,与DPK-means、混合DPK-means算法相比,DPK-F算法误差更小,数据可用性更高。
2.3 算法效率分析
本文在Gowalla数据集和虚拟数据集Data中进行算法效率分析实验。取隐私预算ε=1.0,对比DPK-means、混合DPK-means和DPK-F这3种算法的运行时间,如图7所示。
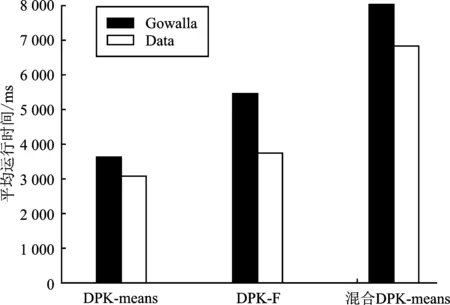
图7 算法运行时间
从图中可以看出,DPK-means算法与DPK-F算法运行时间相差不大。根据图6可知,同一隐私参数下,与其他算法相比,DPK-F算法降低了查询结果误差,提升了查询精确度。与此同时,DPK-F算法较混合DPK-means算法的运行时间缩短了近1/4,在保护位置隐私的前提条件下,降低了查询时间。
3 结束语
为了在保护隐私的条件下获取高精度位置查询,并提升算法效率,本文提出了一种差分隐私模糊聚类位置保护方法(DPK-F)。该方法将差分隐私与改进的模糊C均值聚类算法相结合,使用BIRCH算法确定初始值,引入高斯核函数将原始空间中的点映射到特征空间,选取最终聚类集合的质心点加入符合差分隐私的拉普拉斯噪声来得到每个位置集合的扰动位置点,并使用扰动位置进行查询。实验结果表明,该方法可以降低查询误差,提升算法效率。在今后的研究中,计划引入分布式系统来进一步提升算法效率,并探索DPK-F算法在其它方面的应用。

