基于改进QR算法的矩阵分解器设计
陈文杰,宋宇鲲,张多利
(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)
矩阵分解是矩阵运算中重要的运算之一,在神经网络加速器[1-2]、多进多出(Multiple-Input Multiple-Output,MIMO)[3-5]、自适应滤波器[6]等领域有广泛的应用。常见的矩阵分解法主要有LU分解、QR分解等。LU分解包括Cholesky分解法、Dolittle分解法等。QR分解包括Gram-Schmidt正交分解法(MGS)、Givens-Rotation分解法(GR)、Householder分解法(HT)等。不同的分解法适用于不同的应用场景,在高精度、高稳定性的设计前提下,QR分解凭借其高数值稳定性和对输入矩阵无要求等特点得到了广泛的关注。
在QR分解算法中,Gram-Schmidt正交分解算法的运算并行度高,但数值稳定性较差[7];Householder分解法运算复杂度过高[8],一般不适用于工程应用中;Givens-Rotation分解法在高精度计算时数值稳定性较好,且算法本身存在并行性,易于硬件实现[9]。GR算法最早在文献[10]中被提出,之后大量研究学者对其进行了改进。文献[11~13]采用牛顿迭代法将GR算法中的开方操作省略,降低了算法的资源消耗。文献[14]采用二维阵列结构实现QR算法,提高运算并行度,缩短了分解时间。文献[15]采用细粒度并行的Givens分解算法,缩短了分解的运算周期,使其具有良好的可扩展性,结构也更加简单。现有GR算法的硬件实现研究大多基于低维度、低精度的硬件实现,有关高维度、高精度的矩阵分解电路的研究较少。
在信息化高度发展的时代,信号处理系统需要实时输出高维度、高精度的矩阵运算结果[16-17]。因此,本文在深入了解GR-QR算法的基础上,通过查阅矩阵分解算法资料,找到一种基于按列Givens旋转(Column-wise Givens Rotation,CGR-QR)的高并行度算法[18],并基于该算法设计了一种高性能的CGR-QR分解电路结构。该结构消去了QR分解中多次迭代的运算过程,降低了消元过程的运算时间,提高了资源利用率。
1 算法原理
设A为m×n阶非奇异矩阵,Q为m×m阶正交矩阵,R为上三角矩阵,若满足下式
A=QR
(1)
则称其为矩阵A的QR分解[19]。
QR分解中,通过左乘Givens矩阵Gij,更新原矩阵的第i行第j列元素,其他行不变。通过不断左乘Givens矩阵,可将矩阵的一列元素消元。
(2)
其中G矩阵的表达式如下
(3)
c与s为更新因子,表达式如下
(4)
将G的表达式带入式(2)中,得到R(1)的计算式
(5)
式中,bij为需要消元的矩阵的第i行第j列的元素。式(5)中参数K、S、l、P的计算式如式(6)所示。
(6)
根据数学定义,可知矩阵Q为正交矩阵。经过n-1次Givens旋转,原矩阵被转化为上三角矩阵R,如式(7)所示。
R=Qn…Q1A=
(7)
Q=QnQn-1…Q1Q=QnQn-1…Q1也为正交矩阵,R为上三角矩阵,上述过程即为矩阵A的CGR-QR分解。
2 QR分解的相关研究
2.1 QR-RD的细粒度并行结构
文献[15]提出一种并行的QR算法。该算法由一个外循环和两个同级内循环构成,且两个内循环同时进行工作,其更新过程如图1所示。
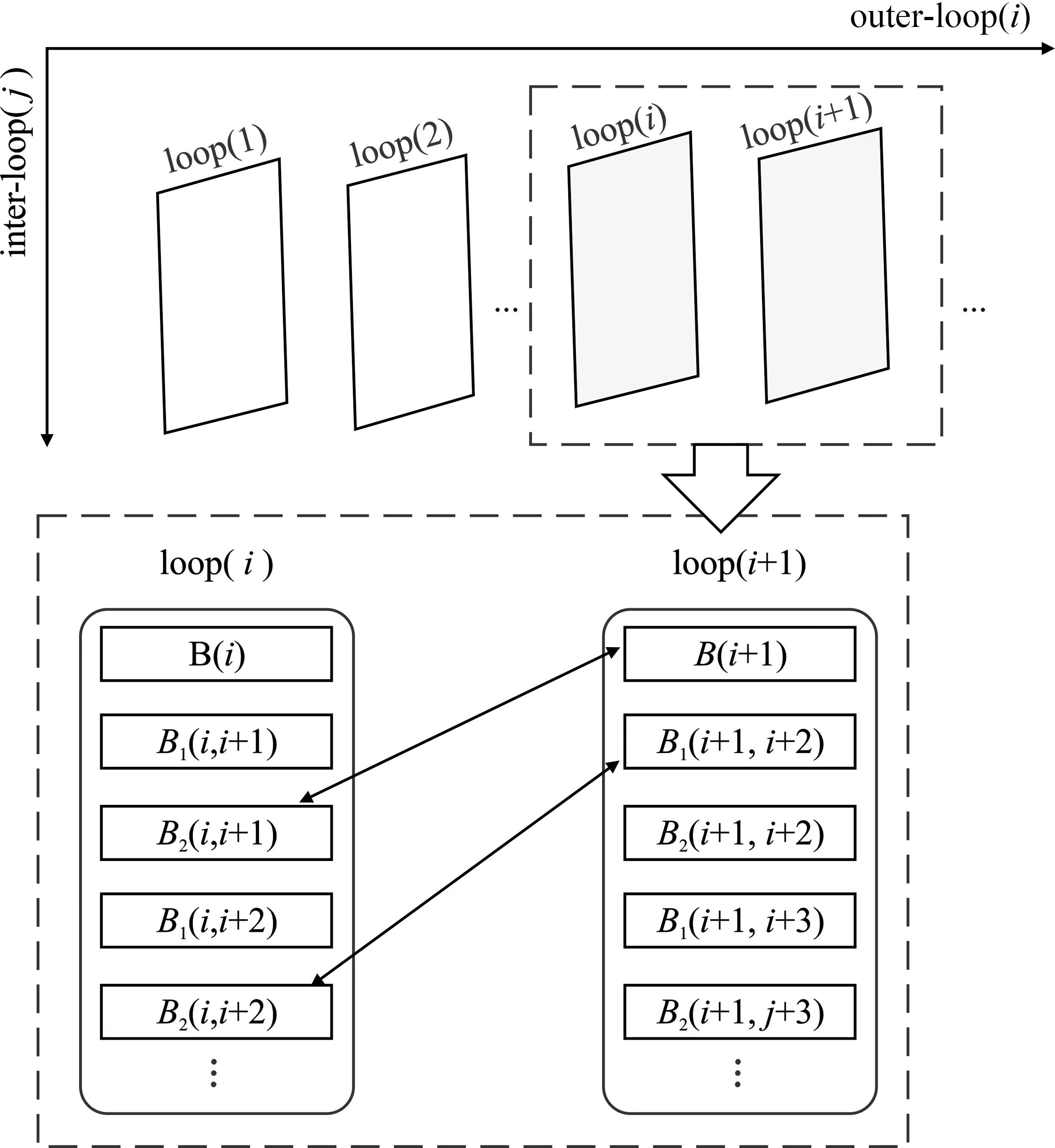
图1 算法更新过程[15]
算法中,B(i)为外部循环中的参数计算过程,该过程负责QR分解过程中更新因子的计算。B1(i,j)为行更新过程,B2(i,j)为更新过程中的参数计算过程。
QR算法分为4个步骤:初始化阶段、计算阶段、同步阶段、存储阶段和待定阶段。每个处理元件(Processing Element,PE)在初始阶段获得其PE标识符(pid)。计算阶段是算法的主要阶段,主要包括接收数据、更新数据和发送数据等阶段,这些阶段并行执行。首个Loop从外部存储器加载数据,之后的Loop从上一级Loop中获得数据。最后一个Loop的结果将更新到存储器中,其余的Loop结果传到下一级Loop中。
算法细粒度并行QR分解算法。
输入:源矩阵Ai。
输出:分解得到的上三角矩阵Ri,共轭转置矩阵Qi。
1.p:the number of PE pid: identifier of the current PE
2.Initial Phase:
3.SetPID[pid];//设置当前标志符
4.Calculating://开始计算
5.if(pid==0)Load(Ai);
6.else Rcv(pid-1,Ai);//判断并加载输入矩阵
7.forj=(i+1),…,n
8.Parallel do 1,2 and 3;//并行计算步骤1、2、3
9.1:if(pid==0)Load(Aj);
10.esle Rcv(pid-1,Aj);//加载当前计算矩阵
11.2:Updata(Ai,Aj);//更新矩阵数据
12.3:if(pid==p-1) Store(Aj);
13.else Send(pid+1,Aj);//判断计算结果输入到下一级还是存储到存储器
14.end
15.wait();
16.Store1(pid,Ri,Qi);//存储分解得到的矩阵Ri和Qi
17.Ready Next Section:
18.Judge(pid);//判断当前标志符是否已经完成分解。
主要消息传递基元的定义为:
(1)Load(X)指从外部存储器中加载数据;
(2)Store(X)指将矩阵X存入外部存储器中;
(3)Store 1(pid,XR,XQ)代表将PE编号为pid的矩阵XR和XQ存储到外部存储器中;
(4)Send(pid,Y)代表将矩阵Y发送到编号为pid的PE中;
(5)Rcv(pid,Y)代表从编号为pid的PE中接收Y矩阵数据。
细粒度并行分解硬件结构如图2所示。
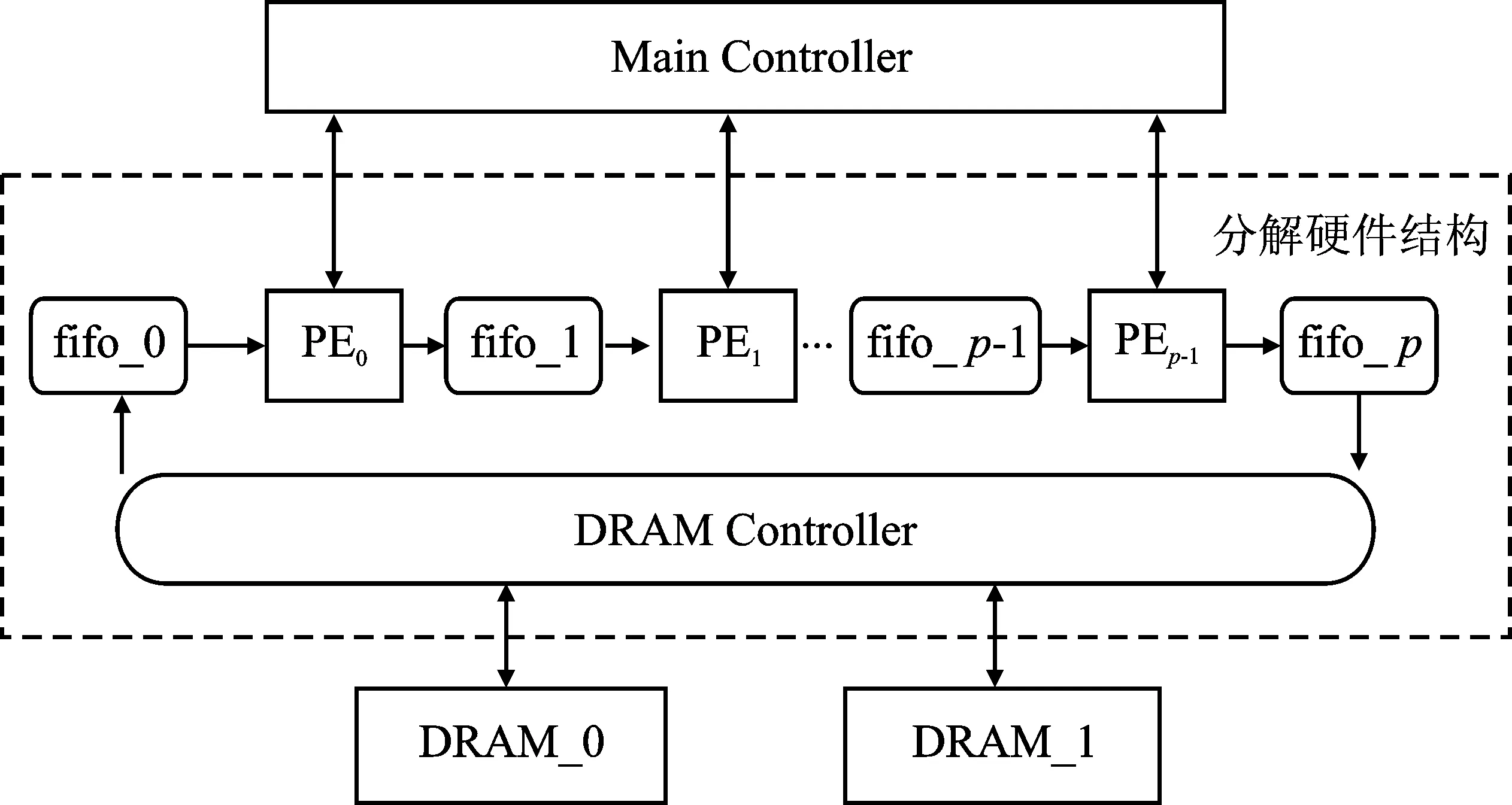
图2 细粒度并行分解硬件结构
细粒度并行的QR分解算法将QR分解为更新因子计算、参数就算、行列更新3个部分,提高了分解过程中的运算并行度。由于该算法延续传统的Gives-QR分解,每一次分解只能更新两行行向量,虽然通过多组PE进行流水操作,但迭代次数并无减少。另外,该结构采用大量的PE堆叠,运算过程中的中间数据需要额外的存储资源寄存,在并行度较高时所需的运算资源较多。对于高速、高精度矩阵求逆器设计而言,需要在算法层面进行更新,消去矩阵元素的数据相关性,从而获得高并行度的实现结构,最大程度挖掘算法的运算性能。综上所述,尽管细粒度并行的分解结构性能优异,但是不适用于高速、高精度大维度矩阵求逆器设计。
2.2 二维阵列结构
在资源充足的情况下,二维脉动阵列分解结构是性能最高的结构[14]。二维阵列采用按堆积资源的方式处理数据更新,数据吞吐量和运算性能较高,其具体结构如图3所示。
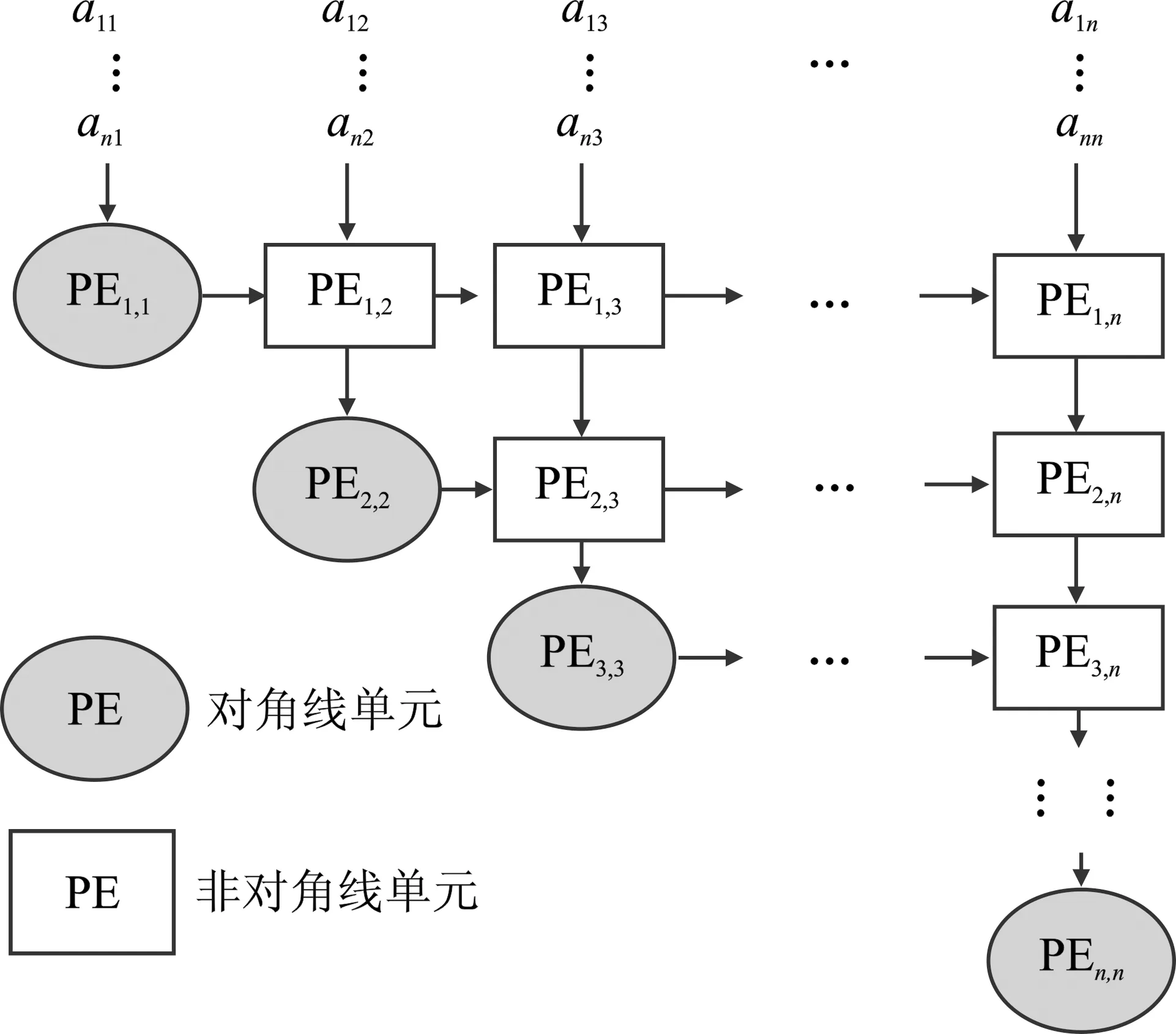
图3 二维阵列结构图
二维阵列由对角线单元和非对角线单元组成。对角线单元由一个Givens生成(Givens Generation,GG)单元和一个Givens旋转(Givens Rotation,GR)单元组成,用于计算更新因子和行列更新。非对角单元由一个GR单元组成,仅用于行列数据更新。对角线处理单元按式(3)计算每一组Givens的旋转因子并向右传递,同时更新该列的数据,并将数据回存至存储器中。非对角线处理单元使用左侧处理单元传递的旋转因子,将该列的当前行元素更新并向下传递。
二维脉冲阵列结构通过堆积资源的方式实现性能提升,在处理一些低阶矩阵时拥有较强的运算性能。但是随着矩阵阶数的增加,运算资源也呈现指数增长的趋势。在高精度计算情况下,更新因子的计算涉及开方和除法运算,硬件消耗巨大。综上所述,二维结构虽然自身性能优异,但不适用于处理高精度高纬度的矩阵求逆运算。
3 优化的CGR-RD分解结构
3.1 基于CGR-RD算法的一维分解结构
由上文可知,二维阵列每次消元时,数据从上一级向下传输。当所有矩阵输入到阵列时,运算并行度达到最高峰,此时参与计算的对角运算单元数量为n/2,非对角单元数量为(3n3-2n)/4。在浮点运算过程中,二维阵列的硬件资源消耗巨大,且资源闲置率较高,因此不适用于实际应用。基于以上原因,本文提出一种适用于2~32阶高精度矩阵分解的一维线性结构,具体结构如图4所示。
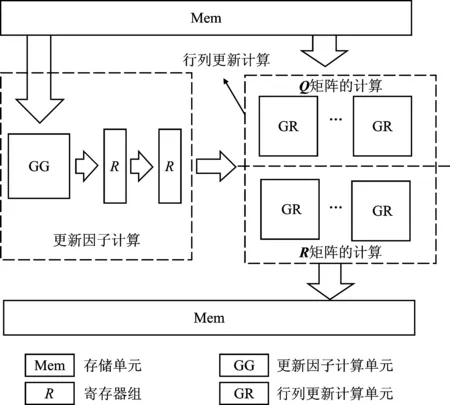
图4 CGR-QR分解一维线性结构
CGR-QR分解结构仅使用一组更新因子计算单元,数据以流水形式传入更新因子计算单元。其采用8组行列更新计算单元并行计算,同时对更新因子计算与行列更新计算的时间进行折叠处理。基于CGR-RD算法的GG单元和GR单元的结构如图5所示。
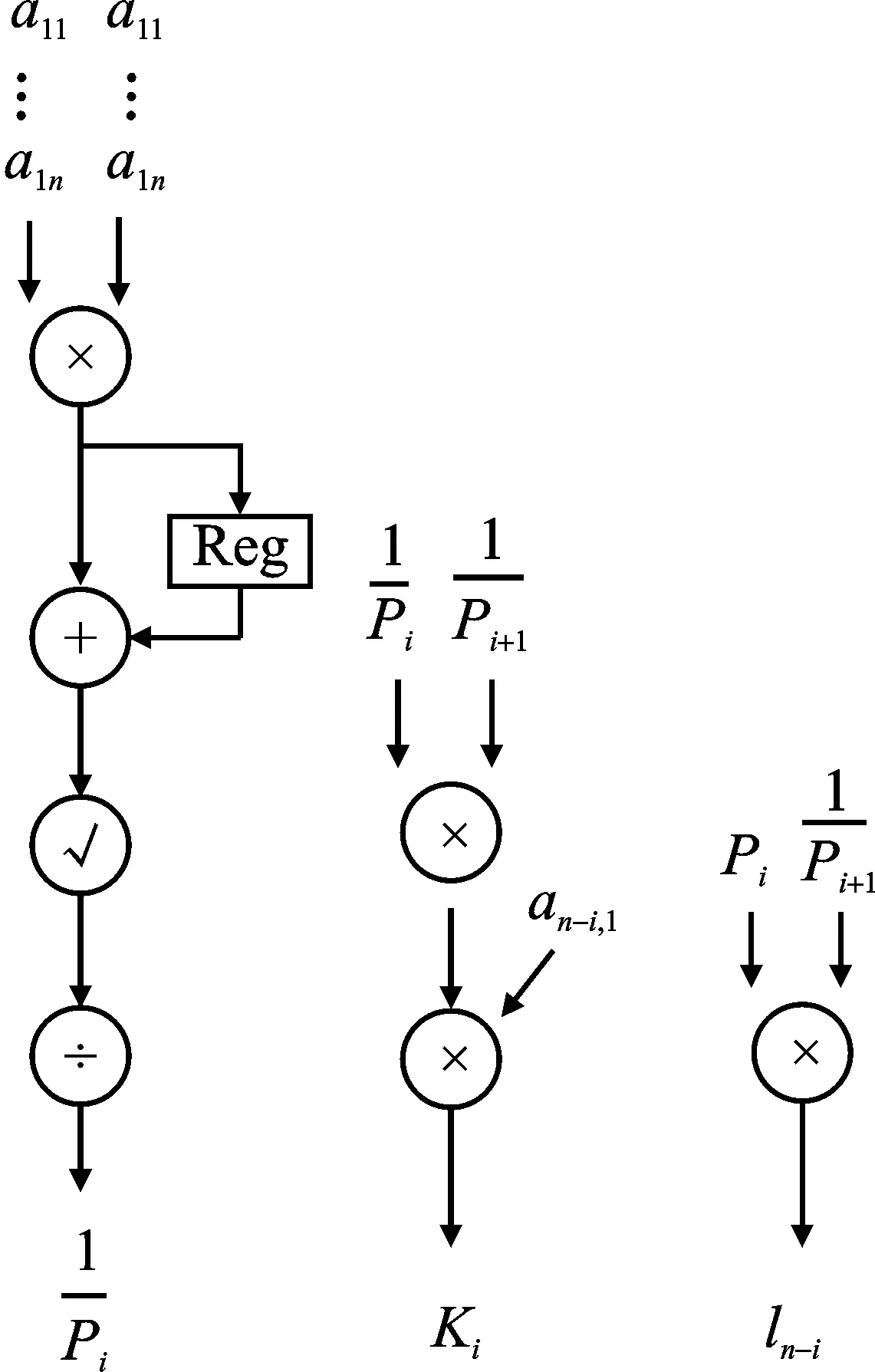
(a)
由式(6)可知,更新因子的计算仅需矩阵中的一列元素,因此当矩阵更新完首列元素后,便可并行计算下一次消元的更新因子。如图6所示,更新因子计算部分分为一个GG单元和两组寄存器组。当GG单元完成第一组更新因子的计算后,将数据写入第一组寄存器组中,第二组寄存器组从上一个寄存器组中读取更新因子,并将其传入GR单元进行行列更新。当GR单元完成首列元素的更新操作后,GG单元从存储器读取更新后的列元素,并进行下一次行列更新的更新因子计算。当计算完成后,将数据写入第1组寄存器。对于n阶矩阵,GG单元和GR单元运行的时间对比如图6所示。
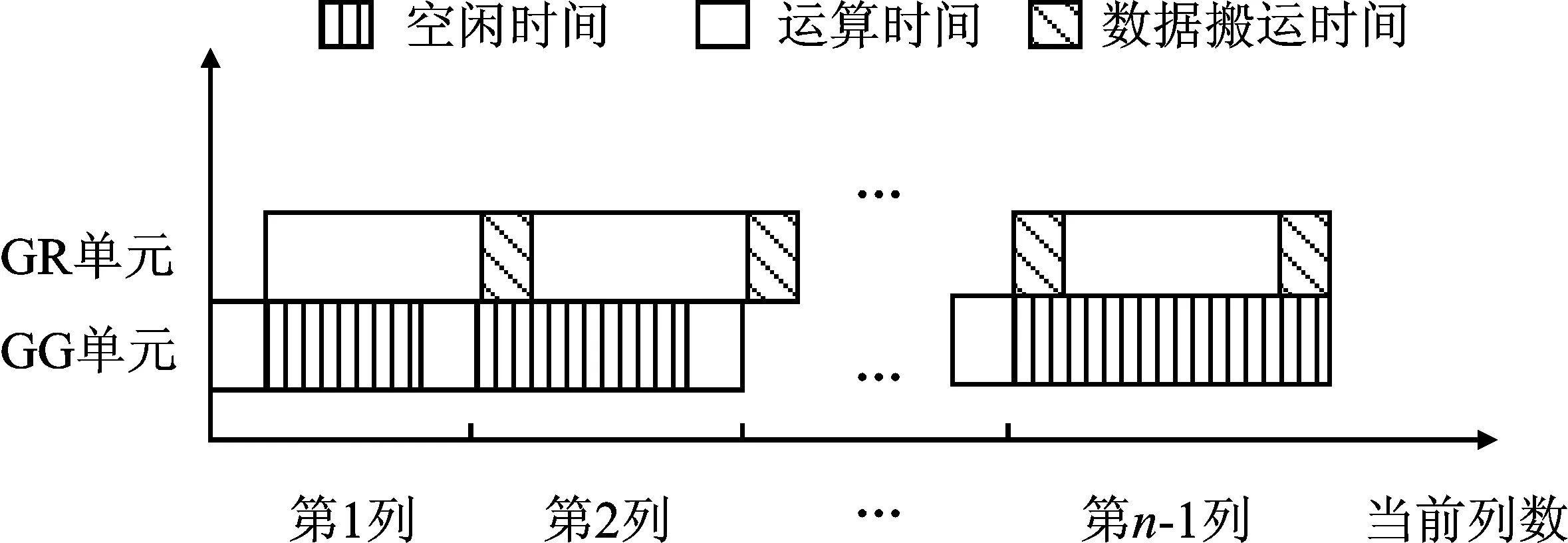
图6 n阶矩阵GG、GR单元运算时间对比图
由图6可知,基于CGR-QR的一维线性结构将GG运算单元与GR运算单元的运算时间折叠,将原本需要n-1次GG单元和n-1次GR单元的运算压缩到仅需1次GG单元和n-1次GR单元运算。
相比于二维阵列结构,该结构的性能损失主要为:当矩阵阶数变大时,由于GR单元的数目要小于矩阵阶数,一维线性结构在行列向量消元的过程中需要[N/4]个运算周期进行消元运算,[i]为向上取整函数。
GR单元的数量决定了该一维线性结构的运算性能,因此加大GR单元的数量可以提高分解的效率。然而当GR单元数量过多时,当前阶段的数据更新会快于下一阶段更新因子的计算,GR单元仍然需要等待更新因子计算,并且当GR数量增大时,硬件资源消耗也将逐渐加大。因此,需要根据更新因子的计算时间和数据更新的计算时间等条件计算出最合适GR单元的数目,计算式为
(8)
式中,TGG为更新因子计算单元的计算时间;TGR为行列更新计算单元的计算时间;M为矩阵运算器兼容的最大阶数;N为GR单元的数量,由于本文的Q和R矩阵是同时得到的,因此N为偶数,其计算式如式(9)所示。

(9)
根据设计指标和实现工艺的情况,本文GR单元的数量N被选定为8,即8组GR单元。
3.2 一维线性结构分析
基于CGR-QD算法的一维线性结构与二维脉冲阵列的理论运算周期数和资源消耗分别如表1、表2所示。

表1 两种结构的理想运算周期数

表2 两种结构的浮点运算器资源理论消耗情况
由于一维阵列的运算资源数和二维阵列的运算资源数不同,故不能单纯地比较两者的运算周期数。本文在一维阵列与二维阵列的运算资源数对等的情况下,选取两者计算单个数据的时间进行比对,结果如图7所示。

图7 二维阵列结构和一维线性结构性能对比图
由图7可知,在矩阵阶数小于6阶时,二维阵列的性能高于一维阵列结构。由于二维阵列的运算资源与矩阵阶数的平方成正比,因此当矩阵阶数逐渐增加时,二维阵列处理单个数据的时间逐渐多于一维线性结构。根据表1可知,在矩阵阶数小于6阶时,一维阵列与二维阵列的运算周期数相差较少。综上所述,在高速高精度矩阵求逆器设计中采用基于CGR的一维线性结构所耗费的运算资源少,运算性能较高,能更好地满足设计需求。
4 硬件验证与性能分析
4.1 验证方案
本文采用Verilog语言实现硬件设计,在TSMC 28 nm工艺下,使用Verdi_VL-2016.06-1与VCS-VL-2016.06对本文设计进行仿真验证,并通过Design Complier软件完成综合实现,最终通过IC-Complier后端流程得到矩阵分解器的专用集成电路(Application Specific Integrated Circuit,ASIC)版图。矩阵分解器的ASIC版图如图8所示。

图8 矩阵分解器的ASIC版图
本文设计采用Synopsys公司DesignWare库中的浮点流水IP,包括浮点加、减、乘、除和开方。经过综合和后端时序调整,设置浮点加法器、浮点乘法器为4级流水,浮点除法器为32级流水,浮点开方器为25级流水,综合考虑运算性能得到GR单元数目为4。本文在分解过程中同时进行Q和R阵的运算,因此GR单元总数为8,双口RAM的数量为8。
4.2 资源和误差分析
本文设计的基于CGR-QR的分解器在现场可编程门阵列(Field Programmable Gate Array,FPGA)上进行了验证,FPGA开发板型号为Xilinx XCV440T,表3为FPGA资源使用情况。

表3 FPGA的硬件资源占用表
本设计通过MATLAB软件在[-100,100]、[-1010,1010]、[-1020,1020]3个范围内随机取数,数值精度为双精度浮点。本文分别测试了4、8、16、32阶非奇异矩阵。MATLAB求逆结果与设计结果误差如表4所示。
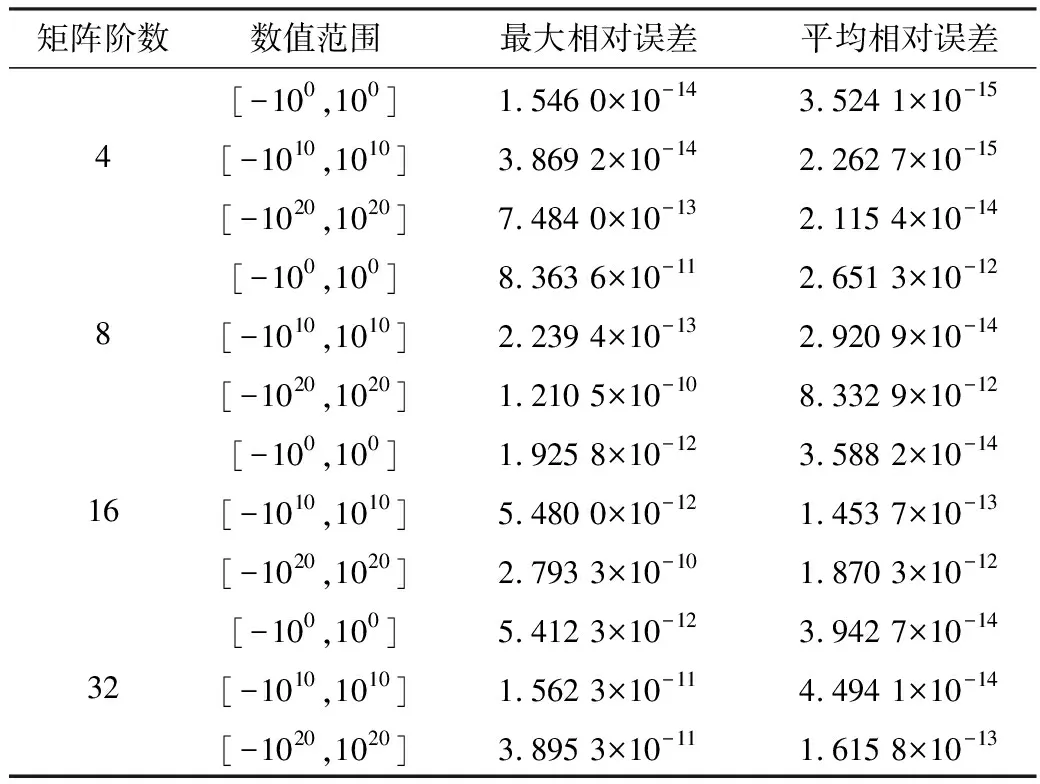
表4 设计结果与MATLAB结果误差
由表4可知,设计结果和MATLAB计算结果的相对误差稳定在10-12~10-15数量级,满足高精度的设计要求。浮点计算器由于精度的限制,在进行计算时会发生截断误差,这是误差的主要来源。由于矩阵阶数相对较小,因此累计产生的误差不大。
4.3 性能分析
不同结构下,矩阵从开始分解到分解结束的运算周期数如表5所示。

表5 3种结构的运算周期比较
相比于传统一维结构,本文采用基于CGR-RD的一维线性结构,将分解过程中的消元步骤并行化,降低了计算时间。相比二维结构,本文结构的运算周期略大于二维结构,但本文设计的分解器在处理高阶矩阵时运算资源消耗较小,且可兼容2~32阶矩阵分解,适用性更好。
另外,本文将所设计的分解器与NVIDIA RTX2070 GPU的CUDA软件进行了对比,两者的矩阵分解周期如表6所示。
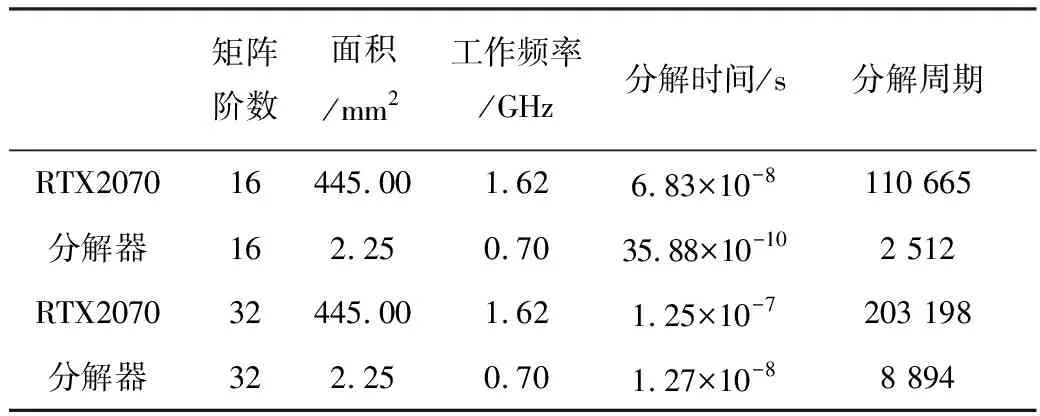
表6 本文分解器与NVDIA GPU的矩阵分解周期对比
表6表明,矩阵规模在32阶以下时,分解器加速效果较好,当矩阵阶数达到32阶时,和RTX 2070 GPU相比,本文设计的分解器相对于RTX 2070的分解周期具有22.8倍加速比。加速的主要原因有两点:(1)高度并行的CGR-QR分解算法;(2)硬件实现中采用一维线性结构,缩短了运算时间。
5 结束语
本文在Givens-QR算法的基础上,根据文献[18]的分解过程,推导出CGR-QR算法中R矩阵和Q矩阵的计算式,并设计了基于CGR-QR算法的矩阵分解器。该分解器采用4路并行的流水结构进行消元计算,减少了运算资源,降低了矩阵分解的运算周期。此外,本文对设计的矩阵分解器进行FPGA和ASIC验证。结果表明,本文的矩阵分解器可以在TSMC 28 nm工艺下,以700 MHz主频工作,其运算结果与MATLAB运算结果的相对误差在10-12以下。当矩阵阶数达到12阶时,该分解器相比于传统一维分解结构达到了2.8倍的加速比。当矩阵阶数为32阶时,分解器的周期数相比于RTX2070达到22.8倍的加速比。综上,本文设计的矩阵分解器满足高速、高精度的设计需求,满足现代信号处理的要求。

