航天器质量特性在线辨识方法及地面验证
徐 旭,张桀睿,王 冠,马广程,夏红伟
(哈尔滨工业大学空间控制与惯性技术研究中心,哈尔滨150001)
随着航天科技的发展,航天器结构变得愈加复杂,新型航天器上往往搭载多种活动载荷,例如机械臂、绳网捕获机构以及视觉敏感装置等。在活动载荷工作时,航天器质心以及转动惯量等质量特性参数会产生一定的改变,给航天器的姿态控制带来一定影响。为保证航天器姿态控制的精度、快速性和稳定性,实时获得航天器的质量特性参数是十分必要的。
在工程实际中,航天器的质量特性往往仅能够通过理论分析或者间接测量获得,例如通过质量特性测量装置测量、质量分解计算以及有限元分析等方法。但这些方法测量精度不高且对参数时变系统无能为力,这就导致了在航天器执行空间任务时,实时变化的质量特性参数会对航天器产生未知扰动,严重影响航天器的性能[1-3]。
对于质量特性变化产生的扰动,可以使用鲁棒性强的控制律来抑制,如滑模控制、模糊控制以及自适应控制。但此类控制律均是被动抑制方法,而质量特性辨识方法则是从根源上补偿了该类扰动,利用惯组等测量元件和飞轮、喷气发动机等执行元件,在线动态辨识出航天器质量特性参数及其改变情况,对控制器参数设计提供依据[4-6]。
Bergman、Williams以及Wilson等人相继提出了高斯二阶滤波辨识方法、基于指数加权递归最小二乘法等算法[7],Wilson提出了基于指数加权递归最小二乘辨识卫星的质量特性参数的方法[8]。基于以上研究,基于最小二乘法的辨识手段在各类工程应用中愈加广泛[9-11]。此外,王书廷、侯振东等人提出了采用推力器组合为激励的卫星质量特性辨识方法,该方法将质心和惯量矩阵进行解耦辨识,减小了耦合带来的辨识误差[12];何骁等针对航天器大角度机动问题,基于卡尔曼滤波的挠性附件振动模态状态估计,提出了一种带挠性航天器转动惯量的辨识方法[13];倪智宇等提出了改进的基于递归预测器的子空间识别(Recursive Predictor-based Subspace Identification,RPBSID)方法并应用于卫星时变模态参数辨识,减小了辨识过程中的数据量,显著节约了在轨辨识过程的计算时间[14]。但以上方法均为离线或半在线辨识,无法满足实时、在线辨识任务的需求,在质量特性动态改变上缺少或具有较差的跟踪性。除此之外,以上方法大都是基于理论和数字仿真层面,缺少全物理试验环节和对实际应用的指导性。
由于航天器工作环境的特殊性,空间任务需要在地面上进行仿真试验验证。目前,国内外许多科研单位已对航天器地面仿真技术进行了相应的研究,且大多数基于数字仿真,而为了充分进行空间任务的地面验证,有必要开展地面半物理仿真以及全物理仿真试验[15]。常用的方法有悬挂法,落体法,液浮法和气浮法,其中气浮法的应用最为广泛[16,17]。我国对基于气浮仿真的航天器全物理仿真系统研究起步较晚,北京控制工程研究所开启了国内三轴气浮台技术应用的先河。随后哈尔滨工业大学和上海卫星工程研究所等单位开展了一系列有关三轴气浮台的研究[18]。
在这种背景下,针对上述航天器质量特性的可辨识性及辨识问题,本文分析了影响辨识模型可辨识性的因素,根据此类辨识模型并基于渐消记忆递推最小二乘辨识理论,提出了一种改进递推最小二乘法的高效率在线辨识方法,与传统方法相比,该方法可解决航天器质量特性在轨实时、在线辨识的任务需求,为高精度姿态控制提供充分的先验信息,解决了以往传统离线或半在线辨识方法实时跟踪性能差,实用性不高的缺点,且具有收敛速度快,跟踪效率高以及辨识误差小的优点;同时为了验证该算法在实际工程任务中的可行性,本文提出了一种基于三轴气浮台的航天器地面全物理仿真系统,通过数字仿真和全物理仿真试验的方式验证了上述算法的可行性,解决了质量特性辨识方法常常停留在理论分析及数学仿真层面上的问题,弥补了质量特性辨识在全物理仿真试验上的空缺。
本文首先针对航天器质量特性辨识问题给出了一类航天器质量特性辨识模型以及其在线辨识算法;然后,针对该类模型分析了其可辨识性的影响因素,提出了一种基于三轴气浮台的地面全物理仿真系统;最后,基于该全物理仿真系统,通过数字仿真与全物理试验两种方法分析了在线辨识算法的收敛速度与辨识误差,验证了该算法的正确性及可行性。
1 数学模型
1.1 坐标系定义
在研究航天器轨道动力学模型中,需对不同的坐标系进行定义,以便于航天器姿态描述。本文中所需要的坐标系定义如下:
(1)地心惯性坐标系
地心惯性坐标系Ox y z原点为地球质心,x轴与地球赤道平面交于春分点,z轴垂直于赤道平面指向地球自转角速度方向。
(2)轨道坐标系
轨道坐标系Ox0y0z0原点为航天器质心,z0轴从原点指向地心,x0轴在轨道面内与z0轴垂直,并指向航天器速度方向。y0轴在轨道平面负法线方向,形成右手正交坐标系。
(3)本体坐标系
本体坐标系Oxbybzb原点为航天器质心。初始状态下,航天器的本体坐标系与轨道坐标系重合,当航天器发生姿态运动时,本体坐标系开始旋转,不再与轨道坐标系重合。
1.2 动力学分析
仅有飞轮作为航天器的执行机构时,航天器的动力学方程为:

其中,J为航天器的转动惯量矩阵;Jf为飞轮的转动惯量;ω为航天器本体转动在惯性坐标系下投影的角速度;ωf为飞轮角速度。
整理式(1)可得动力学差分方程如下:
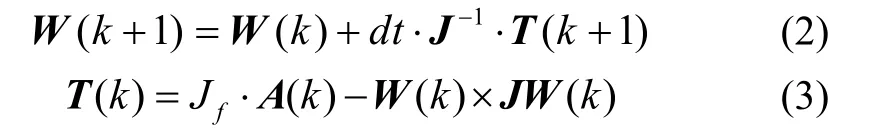
其中
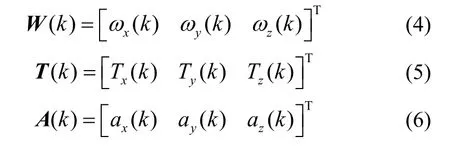
其中ωx、ωy和ωz分别为航天器各个轴的角速度;Tx、Ty和Tz分别为航天器各个轴的输入力矩,该力矩由飞轮提供;dt为系统的采样时间;ax、ay和az分别为航天器三个轴上飞轮的加速度。
1.3 一种改进递推最小二乘法质量特性在线辨识算法
上一小节给出了航天器的动力学模型,本小节根据该模型给出一种改进递推最小二乘法的质量特性在线辨识算法。
定义:

对于实对称阵P,定义:
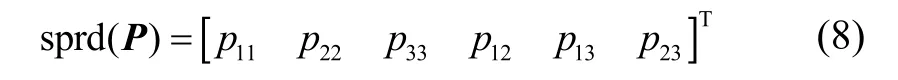
根据系统辨识理论,该航天器质量特性辨识模型的最优解为:
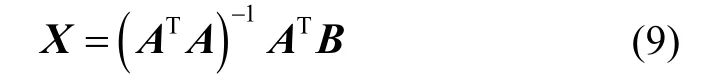
其中
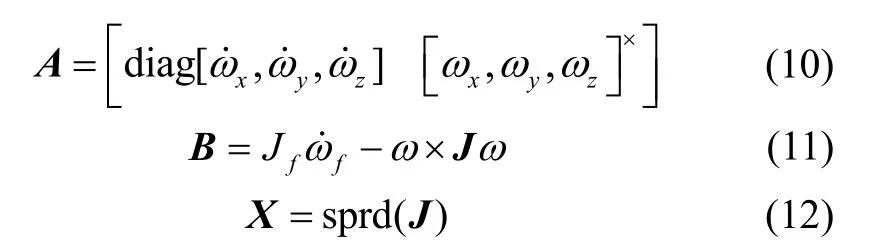
由于基本最小二乘法不适用于具有参数时变特性的动态系统,为了在线辨识出航天器质量特性参数及其实时变化情况,采用改进递推最小二乘法具有更好的效果。
依据式(2)和式(3),可建立以ε1、ε2和ε3为待辨识参数的递推最小二乘公式:

其中,E为单位矩阵;ξ∈(0,1)为收敛因子,用于调节辨识收敛速度。需指出,当选取较大的收敛因子时,迭代运算前期辨识结果振荡幅度越小,迭代过程辨识结果收敛速度越慢;当选取较小的收敛因子时,迭代过程辨识结果收敛速度较快,但前期振荡明显,很容易导致辨识结果发散。因此,在该因子的选取上,需兼顾考虑上述因素,以获得迭代辨识过程的最佳收敛效果。λ∈(0,1)为遗忘因子,通过对旧数据按指数加权,一定程度上衰减旧数据的作用,进而达到辨识数据更新的效果。通常该因子越小,旧数据的衰减效果越明显。
分别对x、y和z轴进行递推运算,可得:
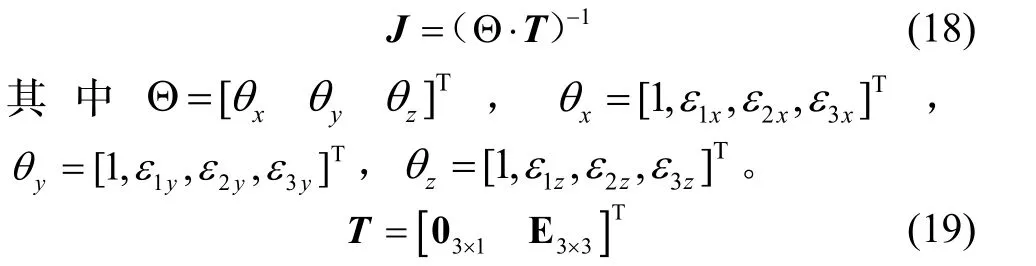
该算法流程如表1所示。

表1 改进递推最小二乘法的在线辨识算法Tab.1 Online identification method based on the improved asymptotic least squares
2 可辨识性分析
在工程应用中,必须要考虑参数的可辨识性,其代表着模型中的每一个参数是否能够通过输入输出的观测数据来确定。如果上述说法对于某一模型成立,则代表着模型是参数可辨识的。
模型的参数可辨识性是模型本身的固有属性,依赖于模型的观测数据,不依赖于模型参数的辨识算法。一种方法是分析辨识模型来得到模型的参数可辨识性。该方法适用于理论证明,但在工程应用中缺少应用性。而工程实际中常用的方法是设计一些激励信号来保证系统是可辨识的。
2.1 模型的参数可辨识性分析

由式(10)知,系数矩阵A由系统的姿态数据构成,故只需姿态数据保证T0>A A成立,即可满足参数可辨识条件2。
同时满足条件1和条件2,该模型参数可辨识。
2.2 激励信号分析
系数矩阵A由航天器输出的姿态数据组成,所以在实际应用中,分析系数矩阵A确定系统参数可辨识性的方法比较被动,我们难以主动地保证系统是可辨识的。为了解决上述问题,我们要主动选择并设计一些激励信号,将模型的参数可辨识性从被动证明转为主动满足。
从系统辨识理论来看,可辨识性与模型的输入密切相关,其依赖于模型的输入输出观测数据。为了保证模型是可辨识的,激励信号要在整个观测周期上持续激励出系统的所有模态。
当系统参数无法通过观测数据辨识出来时,一个原因可能是输入输出的观测数据不合格。换言之很有可能是激励信号无法有效激励出系统的各个模态,不能满足参数辨识的要求,导致系统参数不能正确地辨识出来。
引理2[19]:满足需求的激励信号能够激励出系统的全部模态,使得系统的输出数据包含系统的全部信息,此种信号就被定义为是持续激励信号。
其数学表述为:
对于激励信号r(t)∈R,定义一个n维激励信号列向量:

下式中I为单位阵,若存在整数N≥n和常数α> 0使得以下公式成立:
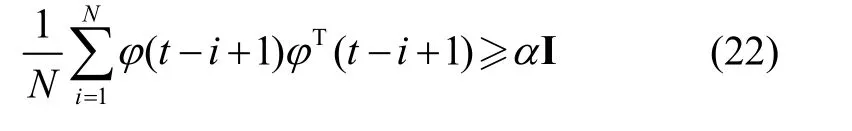
其中
t≥N+n-2
则称激励信号r(t)是n阶持续激励信号。该条件被称为是持续激励条件。
其中正常数α在不同的激励信号背景下是有不同取值的。若存在某一待辨识系统有n个参数,则要求其激励信号至少要满足n阶条件。除此之外,对于确定性系统或模型,其激励信号不需要对每一个持续激励条件中的t都成立,只需存在一个t≥N+n-2使得该条件成立即可。
3 地面全物理仿真系统设计方案
为了提高算法的部署效率,本文研究了基于三轴气浮台的航天器地面全物理仿真系统的设计与实现,并将本文所提算法在该系统中进行试验、分析与验证。
3.1 系统组成
基于三轴气浮台的航天器地面全物理仿真系统分为台上综合试验系统和台下监控系统。
台上试验系统由三轴气浮台及仪表平台、台上管理控制单元、电源模块、调平衡模块、数据传输功能模块、转动惯量测量模块等组成,如图2-3所示。仪表平台主要为台上试验系统各组成部分提供硬件安装接口;台上管理控制单元主要完成以下功能:

图2 三轴气浮台实物图Fig.2 Physical drawing of the three-axis air bearing testbed
(1)对台上的调平衡模块的控制;
(2)对姿态测量信息的采集和管理;
(3)对台上的电源模块进行综合管理和控制;
(4)对台上仿真试验参试设备的控制和管理;
(5)对台上工作状态的记录系统控制和管理。
电源模块用来给台上试验系统所有电气设备供电;调平衡模块用于三轴气浮台于试验前的质心调节工作;数据传输功能模块用于收集台上所有实验数据以及各设备的工作状态并发送给台下监控系统;转动惯量测量模块负责辨识分析三轴气浮台的转动惯量参数。
台下监控系统由数据传输功能模块、安全辅助功能模块以及台下监控软件组成。数据传输功能模块负责接收由台上数据传输功能模块发送来的实验数据;安全辅助功能模块包括伞状支撑和千斤顶,分别用于三轴气浮台运动限位以及支撑;台下监控软件用于显示、分析、存储和回放该实验数据,并向台上综合试验系统下达控制指令。
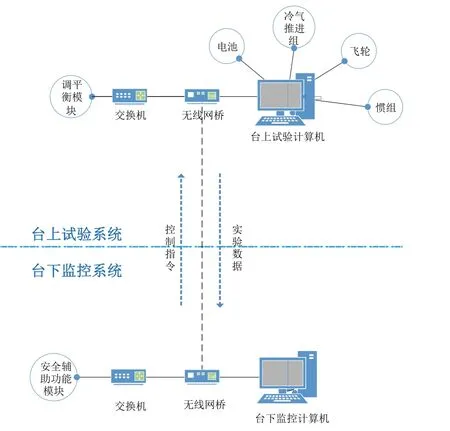
图3 地面全物理仿真系统组成示意图Fig.3 Ground full physicssimulation system compositi on diagram
3.2 工作原理
三轴气浮台通过供气系统向气浮球和球轴承中提供压缩空气形成气膜来使其仪表平台浮起,来模拟卫星在轨时微干扰力微干扰力矩的动力学环境。
通过在三轴气浮台上安装星上载荷、星载计算机、惯性测量单元以及角动量交换装置等设备来搭建三轴气浮台的测控系统。再配置好其微干扰力矩的工作环境,包括降低环境风干扰,调节三轴气浮台质心至其旋转中心位置,减小重力偏心矩的影响,来使其承载的试验系统满足试验要求,以完成卫星在轨动力学的各项地面试验工作。
4 数字仿真与地面全物理试验分析
第一节给出了航天器在轨动力学模型以及质量特性在线辨识算法,第二节给出了模型的参数可辨识性,本节通过数学仿真以及地面试验验证该辨识算法的正确性与可行性。
4.1 数字仿真分析
设该仿真模型中,航天器的转动惯量矩阵J(单位为kg·m2)为:

设该模型中三个轴上的飞轮输出幅值为±100mNm的力矩方波信号,信号周期分别为14s,16 s和18s,采样时间为0.02s;初始化辨识信息θ(0)=0,P(0)=αI,α=106~1010;设置遗忘因子λ=0.99,收敛因子ξ=0.15。得到的辨识结果如图4-6所示。

图4 Jx辨识仿真结果对比图Fig.4 Jxidentification simulation result comparisonchart
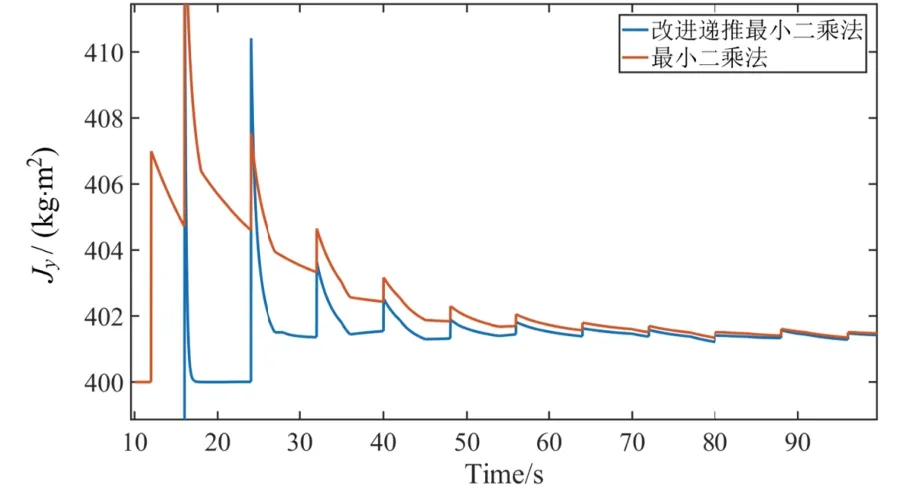
图5 Jy辨识仿真结果对比图Fig.5 Jyidentification simulat ion result comparisonchart
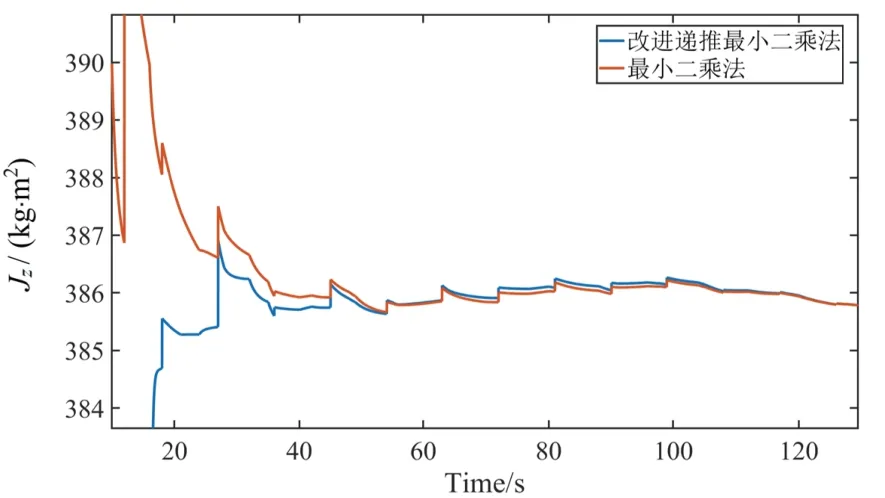
图6 Jz 辨识仿真结果对比图Fig.6 Jzidentification simulation result comparisonchart
改进递推最小二乘法和传统方法仿真结果精度一致,分别为Jx= 386.4 kg·m2,Jy=401.7kg·m2以及Jz= 385.6kg·m2,误差率分别为1.2%,0.7%和1.6%。如图7所示,以每5s数据变化率小于0.5%作为收敛指标,改进递推最小二乘法较传统方法具有更快的收敛速度,在实际应用中更具优势。

图7 辨识仿真结果对比图Fig.7 Identification simulation resultscomparison chart
4.2 地面全物理仿真试验分析
下面通过地面全物理仿真试验来验证本文算法的正确性与可行性。在试验过程中,三个轴上的飞轮力矩为该系统的力矩输入,通过该力矩信息以及惯性部件采集到的姿态数据即可辨识出转动惯量矩阵。用于该项地面试验的三轴气浮台的真实转动惯量矩阵(单位为kg·m2)为:
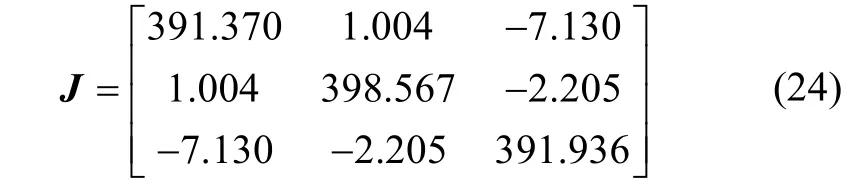
令三轴气浮台x,y和z轴上飞轮输出与仿真分析中相同的力矩方波信号,即信号幅值为±100mNm,信号周期分别为14s,16s和18s。采样时间为0.02s,辨识得到三轴气浮台各个轴转动惯量如图8-10所示。

图8 Jx辨识结果图Fig.8 Jxidentification result c hart

图9 Jy辨识结果图Fig.9 Jyidentification result chart
辨识得到的三轴气浮台各个轴的转动惯量分别为Jx= 402.4 kg·m2,Jy=408.1kg·m2以及Jz= 406.7kg·m2。误差率分别为2.8%,2.4%以及3.8%。
试验时还分析了数据采样时间对辨识精度的影响。分别选取数据采样时间为0.01s,0.02s,0.04s,0.05s和0.1s,得到了不同收敛速度下的辨识结果如图11-13所示。
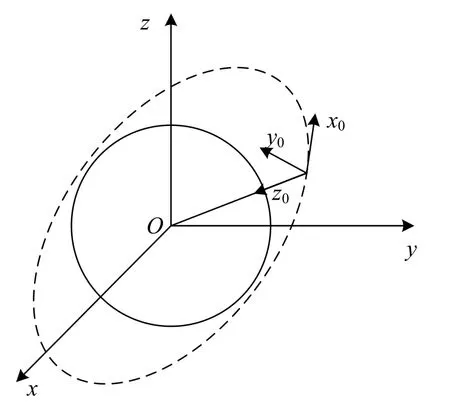
图1 坐标系定义图Fig.1 Coordinate system definition diagram
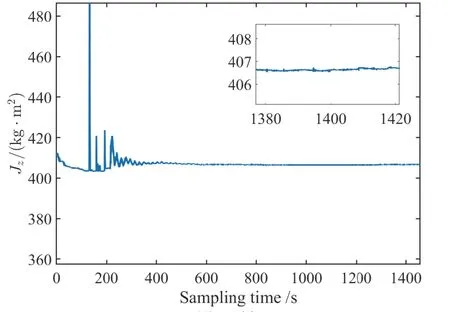
图10 Jz辨识结果图Fig.10 Jzidentificati on result chart

图11 Jx在不同数据采样时间下的辨识结果Fig.11 Identification resultsof Jxat different sampling times
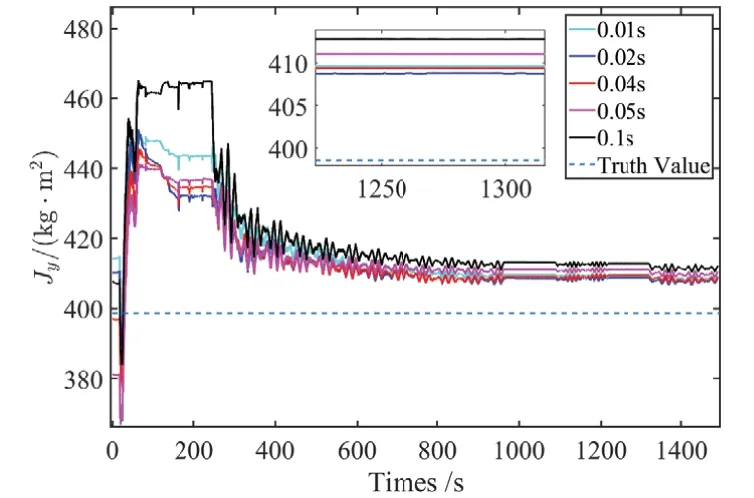
图12 Jy在不同数据采样时间下的辨识结果Fig.12 Identification resultsof Jyat different sam pling times

图13 Jz在不同数据采样时间下的辨识结果Fig.13 Identification results of Jzat different sampling times
地面全物理仿真试验结果讨论:
(1)由于地面试验中惯性测量单元采集到的姿态信息会不可避免地存在环境干扰及噪声,所以在不同的数据采样时间下,会得到不同的转动惯量辨识收敛速度和结果。
(2)在该次地面试验的平台及环境条件下,采样时间为0.02 s下的辨识收敛速度最快,辨识误差最小,为2.8%。除采样时间0.01 s以外,采样时间越长,辨识收敛速度越慢,辨识误差越大。
(3)采样时间为0.01 s时放大了测量噪声对辨识的影响,导致其辨识误差及收敛速度不如采样时间为0.02 s的。
(4)五种数据采样时间下的辨识误差率均在4.5%以内,满足工程应用需求。
通过本次仿真分析以及地面试验,充分验证了本文给出的转动惯量在线辨识算法的可行性与有效性。
5 结论
本文针对航天器质量特性在线辨识问题,提出一种高效率在线辨识方法和地面全物理仿真试验系统。通过建立适用于航天器转动惯量辨识的数学模型,分析了其可辨识性和数据采样时间的影响机理,基于渐消记忆递推最小二乘辨识理论,提出了一种改进递推最小二乘法的在线辨识方法。为了验证在线辨识方法的正确性与可行性,本文设计了一种基于三轴气浮台的地面全物理仿真试验系统。数学分析表明,改进递推最小二乘法的在线辨识方法收敛速度优于传统辨识方法;全物理试验表明,该算法的辨识精度优于96.2%,验证了本文提出的航天器质量特性在线辨识方法的可行性与高效性,突出了该方法具有实用性强、精度高、收敛速度快的优点,对航天器质量特性在线辨识的算法设计和地面验证具有一定的参考应用价值。

