软土固结沉降规律及其蠕变特性试验研究
胡伦俊 原战辉 张继平 魏浩 汪亮 朱俊铸

【摘要】利用成都天府国际机场具有代表性的北一跑道现场监测资料,分析软土地基在固结沉降过程中的规律变化,计算地基土的平均应力固结度。并采用与现场填料相同的砂:泥=2:8的混合填料进行蠕变特性试验研究。结果表明,在软土地基中,软土厚度越大,平均固结度将会越小,土层的固结效果也随即减弱。试样在不同的压力级下都会产生较大的瞬时沉降,颗粒破碎主要集中在压实阶段,随蠕变时间增加,试样蠕变会经历明显的衰减蠕变和稳定蠕变2个阶段,蠕变速率趋于0,蠕变量也逐渐达到某一定值,与现场监测结果吻合。
【关键词】软土固结沉降;平均固结度计算;混合填料;蠕变试验
【中图分类号】 TU447【文献标志码】 A
随着经济发展,西南地区基础建设事业蓬勃发展,不可避免会出现山区填方地基工程。山区地形复杂,这些填方工程通常又具有填方体量大、填方高度高,分层施工[1-5]等特点,且填方区常存在较厚的软土层,不适用换填法[6-8]。填方材料多是就地取材,一般为砂泥岩混合物,泥岩占比较大,但同时也存在较多粗颗粒填料。国内外许多学者早已重视对软土地基沉降沉降及粗颗粒的蠕变研究[9-12]。汤斌[13]探讨了软土固结蠕变室内试验的方法并总结了武汉地区典型的软土固结蠕变变形规律,拟合了软土固结蠕变变形的经验公式。聂超[14]用一维侧限压缩试验仪对粗粒填料蠕变缩尺效应进行研究。Yangshen等[15]研究了荷载循环主应力旋转作用下软土地基的沉降规律。结合德国标准的经验沉降公式和动力放大方程分析,得到了考虑共振的简化沉降计算方法。本文依据西南某新建机场北一跑道某个具有代表性的区域来进行固结沉降规律分析,计算其平均固结度,并进行蠕变特性试验。
1表层沉降及分层沉降规律分析
在天然情况下,当软土地基中没有人造排水体时,其排水路径主要为软土之间的孔隙传递,排水路径较长。固结时间和排水距离的平方成正比,土层越厚,固结时间越长,软土固结就越困难。在实际工程中,软土厚度一般难以改变,大面积的换填不切实际,所以要加快软土固结速度主要的方法为减少排水距离,可采用碎石桩或排水板的地基处理方式,使得土体中的水有了水平和竖向通道,减小了孔隙水直接在土颗粒之间传递的比例,缩短了排水距离,有利于加快固结速度,提高软土承载力,。
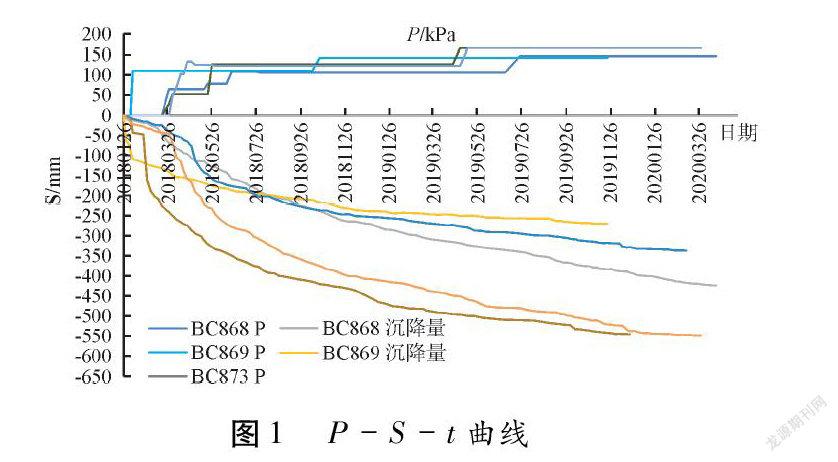
北一跑道部分地表沉降观测点 P-s -1(荷载-沉降-时间)曲线如图1所示,该区域所选用的表层监测点的地基处理方式均为碎石桩+排水板。沉降速率曲线(以 BC868, BC886为例)如圖2所示。
此区域原位监测数据由2018年1月26日—2020年5月13日,共计848天。其中沉降量最小的表层点为 BC871,总的沉降量为-247.8 mm,沉降量最大的表层点为 BC872,累计总沉降为-631.8 mm。将以上表层点所在软土厚度,堆载高度及最终累计沉降量总结至表1。通过表1的表层监测数据可以看出软土厚度越大,其累计沉降越大,软土4-1(粉质黏土)比软土5-1(可塑黏土)沉降更大,且差异较大。由图1可以看出当软土地基处于施工加载期时,每一级填筑体加载瞬间,都出现明显的沉降,且沉降量突增,相应的沉降速率也骤增,沉降曲线波动幅度较大。对于黏性土来说,通常原地基在上部高填方自重荷载下的排气、排水固结变形在整个沉降过程中占比最大,其中 BC868约占79.93%,BC872约占86.41%,其余表层点规律类似,不再赘述。当其处于施工间歇期,沉降迅速发展,随着间歇期时间增长,沉降速率开始呈波动下降且逐渐趋于稳定,沉降速率开始明显收敛。此过程是填方体在自重下的小孔隙的持续压密和非饱和土的排气变形。沉降过程曲线近似呈梯形,每一级加载-间歇期联合构成一个近似的沉降台阶。
本文由于篇幅受限,本文仅给出 BC868, BC872的沉降速率曲线。
如图2所示,沉降速率曲线在加载后,都出现一个较为明显的拐点,随时间推移,速率成波动下降,并最终趋于稳定,说明软土在主固结阶段对加载非常敏感。在整个次固结阶段,沉降曲线变化缓慢。当沉降速率近似趋近与零时,沉降过程才算基本完成。BC868的监测时间起点为2018年2月22日,BC872的监测时间起点为2018年6月19日,在当年九月迎来雨季,即在 BC868速率沉降曲线的240天,BC872的速率沉降曲线89天出现未加载,但沉降速率却出现突增的现象。这是由于机场所用填料为非饱和土体,基质吸力不为零,由于土体毛细管的作用,非饱和土对水分具有吸引作用。在降雨条件下,雨水的人渗使土体含水率不断增加,基质吸力越来越小,边坡土体的吸附强度不断降低,即减小了土体抵抗变形破坏的能力。同时由于非饱和土的孔隙由水和空气所充填,降雨加重了水的比例,挤出空气,增加了土体的自重应力,从而导致土体在主固结沉降阶段沉降速率突增。
分层沉降监测数据从2017年5月27日到2020年4月19日,分层填筑完成时间为2019年9月25日,最终填筑高度为16.42 m。填筑分层沉降管上沉降磁环放置编号由下到上分别为分层1~分层5。如图3所示,当处于施工加载期时,每级加载后,分层沉降曲线也会出现明显的拐点,沉降量近似呈线性增加,分层沉降曲线也会出现沉降台阶。随着软土层厚度的增加,其沉降量也逐渐减小。说明在填筑过程中,软土层沉降以上部为主,与表层沉降规律一致。加载完成以后,分层沉降曲线末端近乎水平直线。分层沉降变化曲线每层沉降过程曲线走势与表层沉降过程曲线极相似。软土层埋深越大,其沉降量越容易收敛,收敛后沉降量几乎不再增长。软土层上部的沉降量及沉降速率均比软土层下部大,上部更快也更容易完成固结。
2软土地基应力固结度变化规律研究
在施工中,为减小工后沉降与差异沉降,提高软土地基的承载力和抗剪强度,常采用堆载预压法结合垂直排水的方法进行地基处理。至今广泛应用的是 Terzaghi基于太沙基一维固结理论建立的饱和土体单向固结微分方程[16]。竖直排水沟的设置引起的土扰动会降低扰动区的水平土渗透性和抗剪强度,从而导致排水沟附近土的导水率和超固结比降低,影响土变形。对实际工程而言,计算土层平均固结度更有意义[17]。
由于实测孔隙水压力是某时刻某点得到的具体的孔隙水压力,用其计算得出的地基平均固结度与孔隙水压力值有较大偏差。故需要对具体孔隙水压力的解析解做如下变换,由地基水平向排水平均固结度公式可得:
距竖井轴线 r且 l时刻时的径向孔压;为在 l时刻径向孔压平均值; d e,re为竖井影响范围的直径与半径; d w,rw为竖井直径与半径; r为地基内某点距竖井轴线距离。
当 r=re时, Lr =Lre。
碎石桩+塑料排水板处理软土地基时,软土地基中存在2种不同的排水体,而研究区碎石桩和塑料排水板的布置均为等边三角形,间距均为1.5m,故其竖井影响范围的直径d, ,相同,均为d=1.05l。碎石桩的直径为0.6m,塑料排水板用砂井理论来阐述其排水能力时应将其转换为等效直径的砂井来计算,塑料排水板的等效直径可按d. =2(b + 8)来计算,其中b为塑料排水板的宽度, δ为塑料排水版的厚度,则在本研究区范围内的塑料排水板 d w =0.067 m。碎石桩与塑料排水板的有效工作范围相同,实际直径不同,因而碎石桩与塑料排水板的井径比也不同。碎石桩的井径比 n 1=2.625,塑料排水板的井径比 n 2=23.5, F(n 1)=0.0127,F(n 1)=2.41。研究表明,井径比 n 越小其固结度越高,本文研究对象碎石桩的井径比远小于塑料排水板的井径比,且在长期固结作用中,碎石桩的耐久性能较好,故计算软土地基长期固结效果时,忽略塑料排水板井径比带来的影响,仅使用在塑料排水板与碎石桩共同排水作用下的孔隙水压力估算软土地基固结度,由此得出的软土地基固结度比实际软土地基固结度偏小,偏于保守。
根据实测超静孔隙水压力观测结果μre确定排水板地基固结度的表达式如下:
以该机场部分断面不同位置处的超静孔隙水压力观测数据为例,据式(3),计算软土层不同深度处的平均应力固结度。
在跑道中心轴线处,随着高程的负增长,平均固结度相应减小。在保守估算下均达到99%以上,说明碎石桩+排水板联合堆载预压法处理地基的效果较好,大大缩短了排水路径,固结情况较好。软土层以排水板的水平向固结为主,排水板缩短了排水路径,故对地基的固结沉降起到了加速的作用。
3砂泥岩混合料蠕变特性试验
3.1试验设备与方案
单轴压缩试验以机场填筑体为原型。试验所用的侧限单轴压缩仪组成结构如图4所示。
试验在一定含水率,一定压实度的条件下对配合比为砂:泥=2:8的砂泥岩混合料进行单轴压缩试验。根据击实试验可以发现,当含水率为9.5%时,试样能最接近其最大干密度,以此能最大程度达到设计的压实度,故本次试验试样的含水率为9.5%。根据机场填筑体设计方案,控制试验的压实度为90%。
3.2侧限压缩试验结果分析
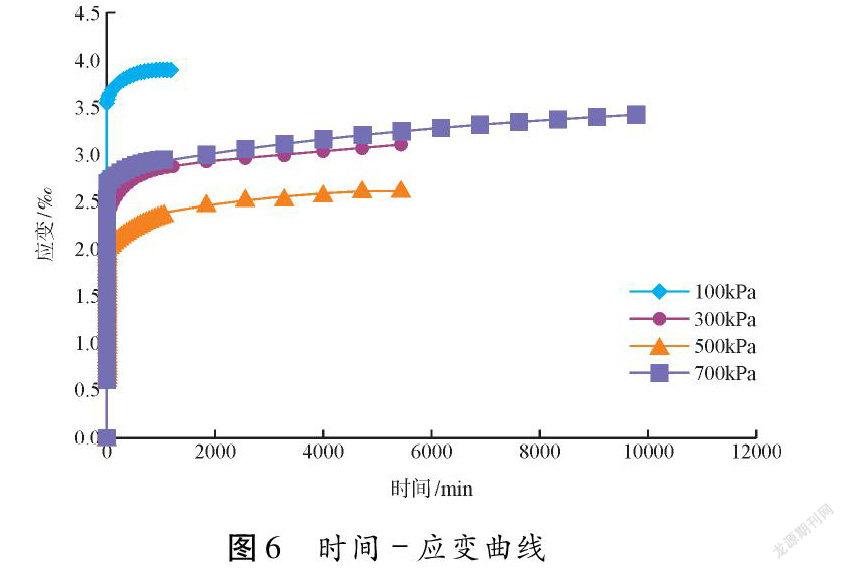
由图5可以看出,试样在不同的压力级下在最初很短的时间内就能产生较大沉降。在施加每级竖向应力时,由于较前一级稳定状态的应力都是瞬时增大到下一级预定压力值,故随着应力的瞬时增大其试样也会瞬间被压缩从而产生了较大的瞬时沉降,土体的性质决定了瞬时沉降中包含了部分瞬时的塑性变形及部分可恢复的瞬时弹性变形。如图6所示,试样在每级压力下随着试验时间的增加,其蠕变速率逐渐降低,直至其蠕变速率接近于零,即应变-时间曲线逐渐接近于水平,试样的蠕变量逐渐到达某一定值而不再发生变化。上述结论与现场原位监测沉降数据吻合,说明試样在蠕变过程中经历了明显的衰减蠕变和稳定蠕变2个阶段。
通过对砂泥岩混合料单轴压缩试验应变-时间曲线进行分析可以发现,其时间的对数值与应变呈现很好的线性关系,故选取对数函数模型对蠕变应变与时间的关系进行表述。即:
式(4)中, t0为蠕变的起始点,分析试验数据可知,应力加载之初都存在显著的瞬时弹塑性变形,而后变形逐渐变慢,综合分析,选取应力加载60 min 时作为蠕变的起始点。a 为蠕变与时间关系拟合曲线的截距,b为其拟合曲线的斜率。
从图7与表3可以看出,蠕变应变与时间的对数呈现良好的线性关系,其拟合度在0.97以上,拟合情况良好,证明拟合参数可用。对于试样在不同压力下蠕变应变与时间的对数拟合曲线的截距及斜率进行分析(图8、图9),可以发现,随着压力的逐级增加,截距的累计量及斜率与压力之间存在关系: b=ca2+da+e。
对蠕变模型应变量进行求取后,得到应变-时间曲线图,并与原始试验曲线图进行对比。
由图10可以看出试验原始应变曲线与经验公式蠕变模型的蠕变曲线拟合程度较高。说明其模型选取合理,对数模型适用于砂泥岩填料的蠕变模拟。模拟的曲线也具有明显的衰减蠕变及稳态蠕变阶段,且稳态阶段的蠕变速率也呈衰减趋势,与实际情况相符合。
将试验数据进行整理,得出试样在不同压力级下的累计应变,做出应力-应变图。
根据图11可知,试样在100~500 kPa应力作用下,其增长近似线性,500 kPa时出现小幅拐点,500~700 kPa应变增长量较前面各级应力明显有所增加,推测是由于在大于500 kPa的应力下,砂岩也将发生部分颗粒破碎,从而导致试样破碎及结构重组引起了更大的应变。故对实验前后砂泥岩混合料进行重新筛分,对其级配及颗粒破碎进行研究。
3.3砂泥岩混合料颗粒破碎结果分析
在试验过程中将压实后及压缩后土样分别取样,缩取样品为固结桶最上层15 cm厚土样。将样品烘干并将固结块尽量捣碎,而后进行电动筛分,计算各粒组含量,并作级配曲线图。对压实后及压缩后的土样的破碎率进行计算(表4、表5、图12)。
砂泥岩混合料在压实阶段和压缩阶段都有一定量的破碎。但是整体来看,压实阶段的颗粒破碎率较压缩阶段来说大很多,整个试验过程中,颗粒破碎主要集中在压实阶段。相对于砂岩,泥岩更加易碎,破碎的小颗粒填充混合料的孔隙,在压力的作用下能更快达到了高度密实的状态,破碎后达到的平衡状态也更加难以打破。
就压缩阶段的破碎率来看,当泥岩含量20%时,压缩过程中破碎的粒径主要集中在0.5~10 mm之间,结合破碎类型分析,试样压缩阶段随着压力的逐级增大,在结构调整的过程中主要发生了破碎和研磨2种类型,还有少数破裂发生。结合砂、泥岩强度特性分析,试样压缩过程中可能少数泥岩发生了破裂,而砂岩主要发生了破碎和研磨,破碎和研磨破碎的量也极少,所以在压缩过程中只发生了微小结构调整,压缩量较小。
4结论
主要研究结论:
(1)该机场软土地基的 P-S -1曲线特点:沉降过程曲线近似呈阶梯状,软土沉降主要发生在填筑加载初期,满载预压后沉降速率逐渐变缓。分层沉降过程曲线的变化过程和趋势与地表沉降过程曲线类似。
(2)试样在不同的压力级下都会产生较大的瞬时沉降,随着蠕变时间的增加,试样蠕变会经历明显的衰减蠕变和稳定蠕变2个阶段。
(3)砂泥岩混合填料蠕变特性可以用对数函数进行表征,对数拟合曲线截距的累计量及斜率与压力之间存在着幂函数的关系式。
(4)试验原始应变曲线与对数函数蠕变模型的应变曲线拟合程度较高。对数函数模型适用于砂泥岩填料的蠕变模拟。
(5)砂泥岩混合料在压实阶段和压缩阶段都有一定量的破碎。整体来看,压实阶段的颗粒破碎率较压缩阶段来说大很多,颗粒破碎主要集中在压实阶段。
参考文献
[1]罗汀,陈栋,姚仰平,等.加载路径对重塑黄土一维蠕变特性的影响[J].岩土工程学报,2018,40(7):1294-1299.
[2]熊乾.高速铁路有碓轨道黄土路基螺杆桩复合地基沉降控制技术研究[D].兰州:兰州交通大学,2019.
[3]张豫川,高飞,吕国顺,等.基于黄土蠕变试验的高填方地基沉降的数值模拟[J].科学技术与工程,2018,18(30):220-227.
[4]梁军,刘汉龙.面板坝堆石料的蠕变试验研究[J].岩土工程学报,2002(2):257-259.
[5]宋二祥,曹光栩.山区高填方地基蠕变沉降特性及简化计算方法探讨[J].岩土力学,2012,33(6):1711-1718+1723.
[6]刘伟,徐捷,蒋浩,等.高填方黄土地基变形规律及稳定性[J].科学技术与工程,2017,17(22):295-300.
[7]徐则民,黄润秋,许强,等.九寨黄龙机场填方高边坡超力稳定性分析[J].地球与环境,2005(S1):290-295.
[8]聂志红,刘群,宋晓东,等.高速铁路砂质板岩粗粒土填料蠕变特性试验研究[J].铁道科学与工程学报,2013,10(3):33-36.
[9] Oda K.,Yokota K. ,Bu L. D.. Stochastic estimation of consolida-tion settlement of soft clay layer with artificial neural network[ J] .apanese Geotechnical Society Special Publication , 2016,2(74):2529 - 2534.
[10]左永振.粗粒料的蠕變和湿化试验研究[D].武汉:长江科学院,2008.
[11]毕港,韦健飞,牛红梅,等.高塑性土蠕变破坏的新模型[J].科学技术与工程,2016,16(23):53-58.
[12] G. R. Me Dowell , J. J. Khan. Creep of granular materials[ J].Granular Matter, 2003 5(3) :115 -120.
[13] 汤斌.软土固结蠕变耦合特性的试验研究与理论分析[ D].武汉:武汉大学,2004.
[ 14]聂超、机场高填方粗颗粒填料蠕变的缩尺效应试验研究[ D].成都:成都理工大学,2018.
[15] Yang Shen, Haidong Xu, Mingan Tao, et al. Settlement of Soft Clay Subgrade Under Coupled Effects of V ibration Frequency and Dynamic Stress Ratio Caused by High - Speed Train Loads [ J]. Soil Mechanics and Foundation Engineering, 2017, 54 (2 ):87 - 96.
[16]郑艳.复杂条件下地铁施工地层变形机理及对桥桩破坏研究[D].阜新:辽宁工程技术大学,2013.
[17]陈仲颐,周景星,王洪锦.土力学[M].北京:清华大学出版社,1994.

