地基不均匀沉降下大型储罐风致屈曲研究*

陈严飞 马尚 董绍华 娄方宇 倪恒 赵永涛 孙秉才

1中国石油大学（北京），油气管道输送安全国家工程实验室/城市油气输配技术北京市重点实验室

2大连理工大学，工业装备结构分析国家重点实验室

3中国石油集团安全环保技术研究院

为满足国家战略储备需要，我国持续建设大型国家原油储备库。目前，大型原油储备基地大多建于沿海地带，且大部分储罐都是在填海造陆形成的软土上建成，软土土质较差、强度低、压缩性大，导致储罐地基易发生沉降，对储罐安全造成不利影响。此外，在沿海地带，储罐易受到强风影响，承受较大的风载荷，大型储罐属于薄壳结构，对外界风载荷作用较为敏感，容易出现屈曲失稳现象，风载荷略微增大也会使储罐罐壁发生较大变形，严重时会引起罐壁撕裂，导致泄漏事故。因此，对于沿海地带的大型储罐的地基沉降问题及风致屈曲问题需要重视。

目前，针对大型储罐地基沉降和大型储罐风致屈曲的研究已取得了诸多成果。陈严飞等人考虑储罐敏感参数提出了罐顶径向位移预测方法[1]。MAHER、PURDY、HOLROYD 等学者通过理论研究、风洞试验等方法，分别提出了风载荷在储罐罐壁上的分布规律[2-4]。郭焕良通过风洞试验，研究了大型储罐的风载荷特征以及罐组的风压干扰效应[5]。浙江大学赵阳教授课题组的林寅通过设计实施风洞试验，获得了敞口储罐、平顶储罐和穹顶储罐的风载荷数据，并对储罐罐壁平均风载荷体型系数进行了拟合，为工程设计提供了参考[6]。魏化中采用数值计算方法，对四种不同容积的大型储罐进行了风致屈曲分析，并在此基础上研究了抗风结构（抗风圈、加强圈）对储罐抗风能力的影响，结果表明抗风结构的存在可显著提高储罐抵抗风载荷的性能[7]。张炜等人采用数值计算方法，对104m3储罐的风致屈曲性能进行了研究，结果表明储罐对风载荷作用十分敏感，在此基础上还研究了包边角钢对储罐抗风能力的影响，结果表明有包边角钢的储罐临界屈曲载荷远大于无包边角钢的储罐[8]。宫建国等人采用数值计算方法，针对10×104m3储罐，分别研究其在静态风压和动态风压下的结构响应[9]。王喆采用数值计算方法，研究了无液状态下不同高径比、径厚比的大型储罐的抗风性能，并与有液状态下储罐的抗风性能进行了对比，结果表明储液的存在可以增强储罐抵抗风载荷的能力，此外还研究了地基倾斜沉降条件下储罐的抗风性能，这也是少数考虑地基沉降与风载荷耦合的研究之一[10]。

学者们在研究时很少有考虑风载荷和沉降载荷两种因素耦合的情况，即地基沉降发生后大型储罐的风致屈曲问题。实际上，建于沿海地带的大型储罐自投入运行起便会开始发生地基沉降，且随着时间推移，地基沉降不断增大，储罐罐壁会产生不同程度的变形，若此时罐壁再承受较大的风载荷，便有可能出现屈曲失稳现象，影响储罐的安全运行。因此，对储罐运行时承受的风载荷进行计算，建立了储罐有限元模型，对未发生地基沉降的储罐进行风致屈曲计算，得到风压作用下储罐的临界屈曲载荷；然后对实测地基沉降进行了傅里叶分解，获得罐周沉降；最后改变储罐的风压驻点周向角，研究了各因素对储罐风致屈曲的影响，可为地基不均匀沉降下储罐风致屈曲研究提供参考。

1 风载荷

建于沿海地区的大型储罐会受到风载荷作用。实际作用于储罐罐壁表面的风压在储罐高度及罐周方向上都按一定的规律分布。大量风洞实验的结果表明，风压在储罐高度方向上的分布变化不大[11]，而在罐周方向上的风压分布可用傅里叶余弦函数表示，其形式为：

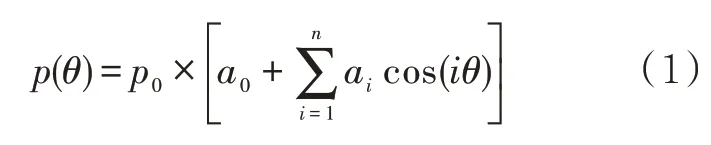
式中：p(θ)为周向角θ处的风压，Pa；p0为基本风压，Pa；i为傅里叶余弦函数的阶数；a0、ai为各阶傅里叶余弦函数的幅值，也称为风压系数，属于经验值，一般由试验或观测得到；n为傅里叶余弦函数的最高阶数。

RISH、GORENC、PIRCHER 等通过研究，分别对风压系数进行了定义[12-14]，国外部分标准规范也对风压系数进行了定义，如EN 1993-4-1 等，具体的风压系数如表1 所示。按照表1 中各风压系数计算得出风压在罐周方向上的分布情况（图1）。

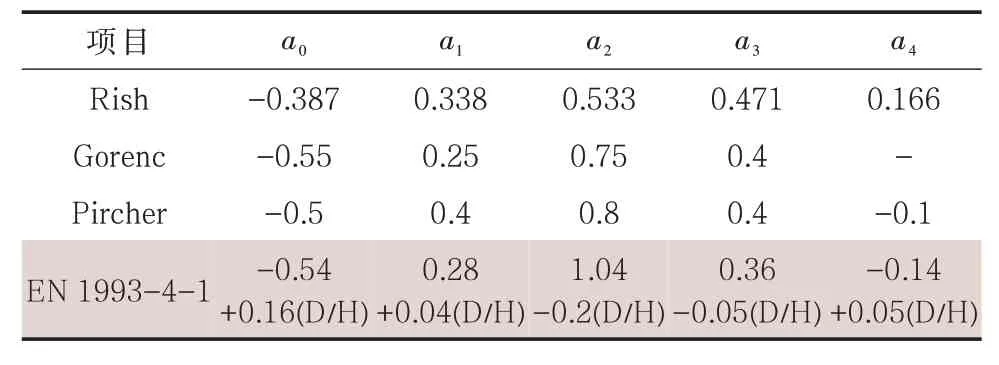
表1 傅里叶风压系数Tab.1 Fourier coefficient of wind pressure

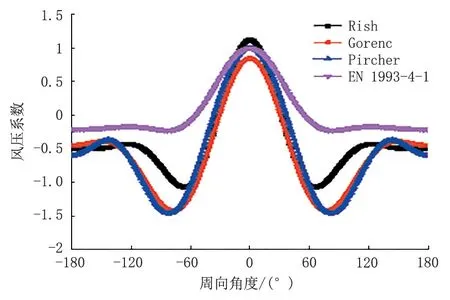
图1 风压在罐周方向上的分布Fig.1 Circumferential distribution of wind pressure on the storage tank

由图1 可知，由各种风压系数确定的风压分布都是关于周向角0°对称的，且在周向角0°处即风压驻点处取得最大值，驻点附近的储罐罐壁属于迎风面；周向角-30°至+30°范围内的储罐罐壁承受风的正压，该范围内的储罐罐壁易发生风致屈曲，而周向角±30°至±180°范围内的储罐罐壁承受风的负压，此范围内的储罐罐壁不易发生风致屈曲；负风压约在周向角±60°至±90°范围内取得最大值。

对比各组风压系数可知，只有EN 1993-4-1 考虑了储罐高度与直径的影响，其他各组风压系数均未考虑储罐结构特征对罐周方向上风压分布的影响，因此在后续研究中，选择EN 1993-4-1 定义的风压系数计算罐周方向上的风压分布。

2 风载荷单独作用下的储罐屈曲计算

2.1 储罐有限元模型

采用我国某10×104m3大型外浮顶储罐的结构尺寸数据建立储罐有限元模型（图2）。所选储罐直径为80 m，高度为21.7 m，底板直径为80.4 m，厚度为20 mm，储罐所用板材钢的弹性模量为2.06×1011Pa，泊松比为0.3。在储罐罐壁顶部设有包边角钢，尺寸为100 mm×12 mm。有限元模型的边界条件为：储罐为空罐；约束储罐底板的径向位移及切向位移，防止储罐发生刚体运动。

图2 储罐有限元模型Fig.2 Finite element model of the storage tank

SCHMIDT 等人曾在其研究中搭建过小尺寸储罐风致屈曲实验模型，并获得了相关实验数据[15]。采用SCHMIDT 等人实验中的储罐结构参数及边界条件建立有限元模型，将有限元计算结果与实验结果进行对比（表2）。由表2 可知，有限元计算结果与SCHMIDT 实验结果十分接近，相对误差仅为1.49%。因此，可以认为建立储罐有限元模型、施加边界条件、计算风致屈曲时采用的方法合理准确，能够用于后续的分析计算及研究。

表2 有限元结果与实验结果对比Tab.2 Comparation of results of finite element model and experiment

2.2 储罐风致屈曲计算

对未发生地基沉降的储罐，首先需确定风压系数。选择EN 1993-4-1 定义的风压系数用于风致屈曲计算（表3）。

表3 风压系数Tab.3 Wind pressure coefficient

采用弧长法对未发生地基沉降储罐的风致屈曲进行计算，记录每个载荷子步的计算结果，得到储罐在整个加载过程中的载荷-位移曲线（图3）。

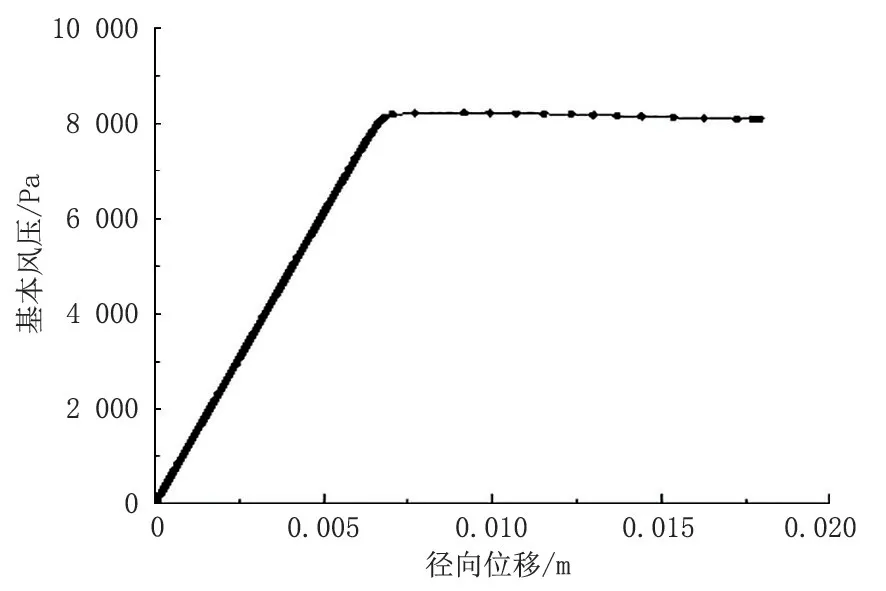
图3 储罐载荷-位移曲线Fig.3 Load-displacement curve of the storage tank

从图3 可以看出：随着载荷的增大，初始储罐径向位移与载荷呈线性关系，当载荷增大至一定值时，储罐径向位移与载荷由原本的线性关系转变为非线性关系，即储罐发生了屈曲失稳，此时的载荷大小即为储罐的临界屈曲载荷。储罐发生屈曲失稳后，储罐失去原本的承载性能，因此储罐在实际运行中承受的风载荷应小于储罐的临界屈曲载荷，保证储罐不会发生屈曲失稳现象。根据储罐载荷-位移曲线，得到未发生地基沉降储罐风致屈曲的临界屈曲载荷为8183.6 Pa。

选择储罐发生屈曲失稳前（p0=7 884 Pa）、发生屈曲失稳时（p0=8 183.6 Pa）、发生屈曲失稳后载荷继续增大（p0=8 213.7 Pa）、发生屈曲失稳后载荷出现减小（p0=8 090 Pa）四种状态的径向位移云图进行对比，观察储罐屈曲失稳过程中的变形情况（图4）。

由图4 可知：未发生地基沉降的储罐因风载荷导致屈曲时，屈曲发生在第四层罐壁处，且位于风压驻点附近；发生屈曲后屈曲位置的径向位移不断增大；屈曲形态表现为局部罐壁发生内凹，使罐壁出现波浪形的“褶皱”。

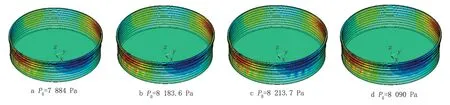
图4 储罐径向位移云图Fig.4 Cloud map of radial displacement of the storage tank

3 地基沉降及风载荷耦合条件下储罐屈曲计算

3.1 沉降参数

选择我国某10×104m3大型外浮顶储罐的实测地基沉降数据用于计算，对该储罐的实测地基沉降数据进行傅里叶分解，将各阶谐波进行相加，即可得到罐周沉降与储罐周向角的关系式，利用此关系式作出罐周沉降的曲线（图5）。

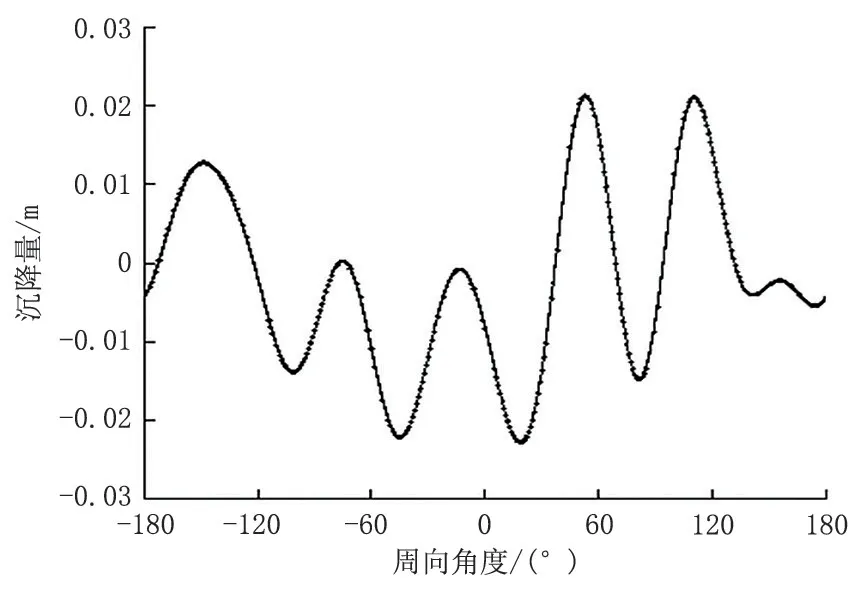
图5 储罐罐周沉降Fig.5 Circumferential settlement of the storage tank

3.2 风压驻点周向角变化时储罐的风致屈曲

地基发生不均匀沉降后，储罐罐壁各处均会产生不同程度的变形，当风从不同方向吹向储罐时，承受风压作用的罐壁结构并不一样，从而对储罐抵抗风致屈曲的性能产生影响，使储罐风致屈曲的计算结果出现差异。以风压驻点周向角0°为起点，改变风压驻点周向角，每隔20°进行一次计算，获得不同风压驻点周向角下储罐的临界屈曲载荷及屈曲形态（表4）。

由表4 可知：不同风压驻点周向角下储罐的临界屈曲载荷存在明显的差异，储罐地基发生不均匀沉降后，罐壁各处发生不同程度的变形，进而对储罐抵抗风致屈曲的性能产生或增强或削弱的作用。

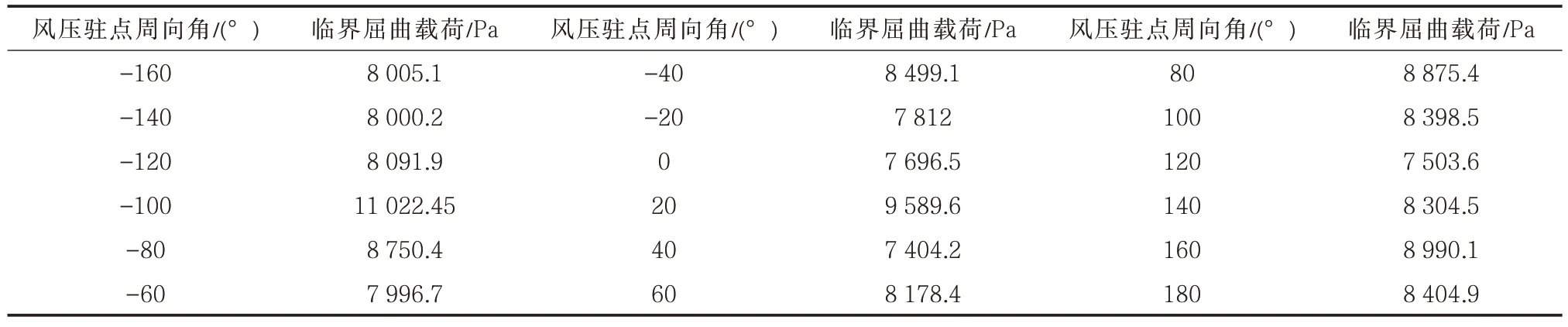
表4 不同风压驻点周向角下储罐临界屈曲载荷Tab.4 Critical buckling load of the storage tank under various circumferential angles of wind stagnation point

为了研究地基不均匀沉降下储罐的风致屈曲机理，考察了不同风压驻点周向角下的地基沉降与储罐临界屈曲载荷之间的关系，以及地基沉降引起的罐壁变形与储罐临界屈曲载荷之间的关系。该储罐不同风压驻点周向角下的地基沉降量如图6a 所示，临界屈曲载荷如图6b 所示，不同风压驻点周向角下储罐局部屈曲处因沉降导致的径向位移如图6c 所示。

由图6 可知：不同风压驻点周向角下的储罐地基沉降量与临界屈曲载荷之间并不存在明显的单调关系，且储罐局部屈曲处因沉降导致的径向位移与临界屈曲载荷之间亦不存在明显的单调关系。因此，不同风压驻点周向角下的地基沉降和储罐局部屈曲处因沉降导致的径向位移与储罐临界屈曲载荷之间皆无直接关系。

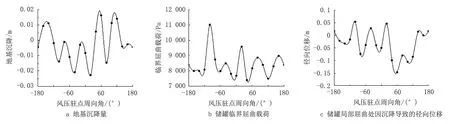
图6 地基沉降、储罐临界屈曲载荷与径向位移Fig.6 Foundation settlement，critical buckling load and radial displacement of the storage tank

根据以上结论可以推测，罐壁变形对储罐临界屈曲载荷的影响并不取决于某一处的变形大小，而是取决于该处附近整体的变形趋势。将不同风压驻点周向角下的计算结果按照储罐临界屈曲载荷是否大于未沉降储罐进行划分，并分别进行详细分析。

3.2.1 储罐临界屈曲载荷大于未沉降储罐的情况

当风压驻点周向角分别为-100、-80、-40、20、80、100、140、160 和180°时，地基不均匀沉降下储罐的临界屈曲载荷大于未沉降储罐。根据以上风压驻点周向角下的计算结果，分别选择以风压驻点周向角为中心±20°范围内、储罐局部屈曲失稳处同一高度附近的罐壁，获得其因地基沉降导致的径向位移，并由此得到该范围内罐壁的变形情况（图7）。

由图7 可知，在储罐临界屈曲载荷大于未沉降储罐的风压驻点周向角下，仅图7b、图7f 和图7h的风压驻点位于储罐罐壁内凹最大处附近，其余情况下风压驻点都位于储罐罐壁外凸最大处附近。再将储罐屈曲失稳处的高度及周向角考虑在内，进行综合对比，结果见表5。

表5 各计算工况屈曲及变形对比(储罐临界屈曲载荷大于未沉降储罐)Tab.5 Comparison of buckling and deformation under various calculation conditions(critical buckling load of the tank is greater than that of the unsettled tank)

图7 储罐局部屈曲处附近罐壁因沉降导致的径向位移(储罐临界屈曲载荷大于未沉降储罐)Fig.7 Radial displacement of the tank wall due to settlement near the local buckling area of the storage tank(critical buckling load of the tank is greater than that of the unsettled tank)

由图7 及表5 可以得出：当风压驻点周向角为-80、100 和160°时，风压驻点位于罐壁内凹最大处附近，不利于罐壁抵抗风压，但屈曲发生在两加强圈之间，加强圈可提高罐壁抵抗风压的性能，两种因素共同作用，最后使临界屈曲载荷有所提高；当风压驻点周向角为-100°时，风压驻点位于罐壁外凸最大处附近，同时屈曲发生在两加强圈之间，两种因素共同作用使得临界屈曲载荷显著增大；当风压驻点周向角为-40、20、80、140 和180°时，虽然屈曲发生于第四层罐壁，加强圈的作用很小，但风压驻点位于罐壁外凸最大处附近，故临界屈曲载荷亦有所增大。此外，无论风压驻点附近罐壁变形是外凸还是内凹，屈曲都倾向于发生在罐壁相对凹陷的部位，当风压驻点附近罐壁变形为外凸时，屈曲不会发生在风压驻点处，而是倾向于发生在罐壁的相对凹陷部位，屈曲失稳处会不同程度地远离风压驻点；当风压驻点附近罐壁变形为内凹时，由于该处已经是罐壁的相对凹陷部位，屈曲倾向于发生于此部位，因此屈曲失稳处距离风压驻点往往不会太远。

3.2.2 储罐临界屈曲载荷小于未沉降储罐的情况

当风压驻点周向角分别为-160、-140、-120、-60、-20、0、40、60 和120°时，地基不均匀沉降下储罐的临界屈曲载荷小于未沉降储罐。根据以上风压驻点周向角下的计算结果，分别选择以风压驻点周向角为中心±20°范围内、储罐局部屈曲失稳处同一高度附近的罐壁，获得其因地基沉降导致的径向位移，并由此得到该范围内罐壁的变形情况（图8）。

由图8 可知：在储罐临界屈曲载荷小于未沉降储罐的风压驻点周向角下，所有风压驻点都位于储罐罐壁内凹最大处附近。再将储罐屈曲失稳处的高度及周向角考虑在内，进行综合对比，结果如表6所示。

图8 储罐局部屈曲处附近罐壁因沉降导致的径向位移(储罐临界屈曲载荷小于未沉降储罐)Fig.8 Radial displacement of the tank wall due to settlement near the local buckling area of the storage tank(critical buckling load of the tank is less than that of the unsettled tank)

由表6 可知：当风压驻点周向角为60°时，储罐局部屈曲失稳处的罐壁高度为12.6m，即储罐屈曲处位于储罐自底向上第一个加强圈与第二个加强圈之间，此时的风压驻点位于罐壁内凹最大处附近，而风压作用会使储罐罐壁发生内凹直至屈曲。因此地基沉降引起的罐壁内凹不仅无法抵消风压的作用，反而会减弱罐壁抵抗风压的性能，进而使储罐临界屈曲载荷减小，以上两种因素综合作用，最终使储罐的临界屈曲载荷相对未沉降储罐略有减小。当风压驻点周向角为-160、-140、-120、-60、-20、0、40 和120°时，储罐局部屈曲失稳处位于第四层罐壁，加强圈对罐壁抵抗风压的性能贡献很小。

表6 各计算工况屈曲及变形对比(储罐临界屈曲载荷小于未沉降储罐)Tab.6 Comparison of buckling and deformation under various calculation conditions(critical buckling load of the tank is less than that of the unsettled tank)

此外，由图8 及表6 可以得出：对于储罐临界屈曲载荷小于未沉降储罐的情况，风压驻点附近的罐壁变形均表现为内凹，而屈曲也都倾向于发生在罐壁相对凹陷部位。

4 结论

储罐地基不均匀沉降及储罐承受的风载荷皆会影响储罐安全运行。通过建立大型储罐数值仿真模型，研究了储罐风致屈曲及地基不均匀沉降下储罐风致屈曲的有关规律。通过对不同风压驻点周向角下储罐的风致屈曲进行计算分析，得到以下结论：不同周向角下的地基沉降与储罐临界屈曲载荷之间不存在直接联系，储罐局部屈曲处因地基沉降导致的径向位移与储罐临界屈曲载荷之间亦不存在直接联系；储罐临界屈曲载荷的变化由储罐发生风致屈曲的位置及风压驻点附近罐壁变形情况共同决定；地基沉降发生后，部分风压驻点周向角下储罐发生风致屈曲的位置会发生改变，由第四层罐壁变为储罐由下至上第一及第二个加强圈之间，此因会使储罐临界屈曲载荷增大，同时改变储罐的屈曲形态；当风压驻点附近罐壁因地基沉降引起的变形表现为外凸时，储罐临界屈曲载荷增大，而当风压驻点附近罐壁因地基沉降引起的变形表现为内凹时，储罐临界屈曲载荷减小；无论风压驻点附近罐壁因地基沉降引起的罐壁变形表现为外凸还是内凹，都不会改变储罐的屈曲形态，并且储罐的风致屈曲都倾向于发生在罐壁相对凹陷部位。