竖井及跌水池体形参数对井喷的影响

张双庆，刘甲春

(1.大连理工大学宁波研究院，浙江 宁波 315016；2.宁波大学土木工程与地理环境学院，浙江 宁波 315211)

强降雨期，雨水的快速填充导致排水管道内水流流态快速地由明渠流转变为有压流，在此过程中部分空气被截留在管道中形成截留气团[1-3]。截留气团在水气的相互作用下发生压缩、移动，气体压力在压缩过程中不断增大[4-6]。高压气团在竖井处释放时会引发大量水气混合物从地表喷出，形成井喷事件[7-8]。井喷喷射高度能够达到几十米[9]，并伴随着剧烈的压力脉动，严重威胁排水系统的安全[10-12]。

国内外学者对排水系统内井喷现象的发生机理进行了研究，发现引发井喷的主要原因为管道中截留气团的释放和惯性作用下水体的振荡[13-14]。快速填充水流冲击截留气团，产生的峰值压力可达到数倍的驱动压力，此部分压力主要用来推动下游水体的加速以增强其输运能力，缓解跌水池内的高压[15-17]。部分学者对井喷的缓解措施进行了研究，如在竖井处安装节流孔板[18]、设置循环水池[19]及导流板[20]、延伸竖井至跌水池中[21]等。虽然这些措施在一定程度上缓解了井喷，但局限于一些特定的条件，且未能充分排出管道中的气体。不同布置形式以及竖井和跌水池体形参数对井喷强度的影响仍未得到充分研究。

本文基于Liu等[12]的1∶20排水系统物理试验模型在ANSYS CFX软件中建立三维数值模型，并利用其试验结果对数值模型进行验证。基于验证后的数值模型，研究上下游管道直径比和相对高度(两根管道底部之间的高度)、跌水池以及排水竖井的体形参数对井喷的影响，分析不同工况下管道内部的压力变化、喷射水量及喷射高度变化，以期能为排水管网系统的设计和安全运行提供参考。

1 数值模型

1.1 模型参数

本文建立了如图1所示的排水系统三维数值模型，模型主要由上游管道、跌水池、竖井和下游管道组成。上游管道的直径Du=0.20 m，长度Lu=5.80 m，坡度iu=0.10%。跌水池连接上下游管道，水池底部长和宽Lc=Bc=0.30 m，高度Hc=0.45 m。竖井位于跌水池上方，直径Dr=0.06 m，长度Lr=1.22 m。下游水平出水管道的直径Dd=0.28 m，长度Ld=5.95 m。

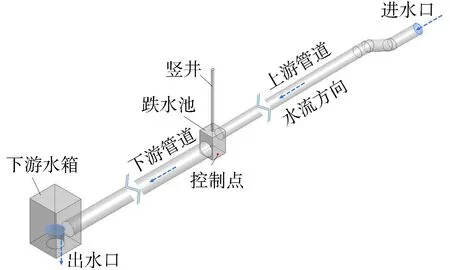
图1 排水系统的三维数值模型示意图

在三维数值模拟过程中，进水口定义为流量入口边界，出水口定义为大气压力边界，管壁和墙面定义为无滑移壁面边界，壁面为光滑壁面。空气为理想气体，水为不可压缩的流体。采用流体体积法(VOF)和基于剪切应力传递湍流模型(SST)的κ-ω紊流模型模拟排水系统中的井喷现象。

连续性方程和雷诺方程(RANS)如下：

(1)

(2)

VOF模型的相方程如下：

(3)

式中α为水的体积分数，α=1表示控制体内完全充满水，α=0表示控制体内完全充满空气。

对于稳态模拟，动量方程和湍流输运方程均采用高阶求解的差分格式。以均方根残差值(RMS)低于10-4和出口水流流量稳定为标准，判断结果是否收敛。对于瞬态模拟，动量方程采用高阶求解的差分格式，湍流输运方程采用二阶向后欧拉格式。当使用二阶向后欧拉格式时，非稳态的湍流方程仍然使用一阶格式，非稳态的体积分数方程将会设定为有限制的二阶格式。

1.2 网格及时间步长检验

为验证三维数值模型在模拟井喷事件中的精度，本文对数值模型进行了网格独立性检验和时间步长敏感性分析，以减小网格数量及时间步长对模拟结果的影响。模拟过程中选择跌水池底部的压力作为控制参数。

通过对跌水池及其周围上下游管段以及竖井进行网格加密，分别对166万、184万、203万和219万网格数量的模型进行模拟分析，控制点(图1)的压力变化如图2(a)所示。当数值模型的网格数量为203万时，跌水池底部的最大模拟压力为33.5 kPa，相比于184万网格下的压力大6.7%，相比于219万网格下的压力小0.9%。进一步增加网格数量不能显著改善数值模拟结果。因此，本文其余工况均采用203万网格数量的模型进行研究。在网格数量为203万时，全局网格尺寸为0.02 m，通过减小局部网格尺寸对网格进行加密，上下游管段、跌水池和竖井的网格尺寸分别为0.012 5 m、0.015 m、0.01 m和0.006 m。

图2 网格独立性及时间步长检验

选取0.000 5 s、0.001 s和0.005 s共3个时间步长进行敏感性分析，模拟压力结果如图2(b)所示。3个时间步长下跌水池底部最大压力分别为32.4 kPa、33.5 kPa、32.4 kPa。0.000 5 s和0.001 s时间步长之间的压力误差为3.2%，0.001 s和0.005 s之间的误差为3.1%。为了平衡计算效率及计算精度，本文数值模拟的时间步长选为0.001 s。

1.3 数值模拟工况

表1给出了本文所有数值模拟工况。工况A系列主要用Liu等[12]的试验数据验证模拟结果的准确性。由于上下游管道存在相对高度，快速填充的水流撞击跌水池壁面后折返进入竖井，将部分气体截留在跌水池内。气团压缩、移动、释放，进而引发井喷。因此，工况B系列主要针对上下游管道的相对高度和管道直径比进行研究。初始状态下跌水池内气体所占的空间大小会影响快速填充过程，进而影响最大井喷压力。“瘦高形”跌水池在相同初始水位下拥有更大的气体空间，对井喷压力有一定缓解作用。因此，工况C系列分别针对Liu等[12]试验模型、“瘦高形”和“矮胖形”跌水池进行模拟，分析相同体积不同高度的跌水池对井喷压力的影响。进入竖井内的水柱将气团截留在跌水池中，高压气团的释放将推动水柱上升。水柱的特性和竖井的体形参数(如长度、直径)对井喷压力有着重要影响。工况D系列针对不同的竖井体形参数进行了研究，以分析竖井参数对井喷压力的影响。

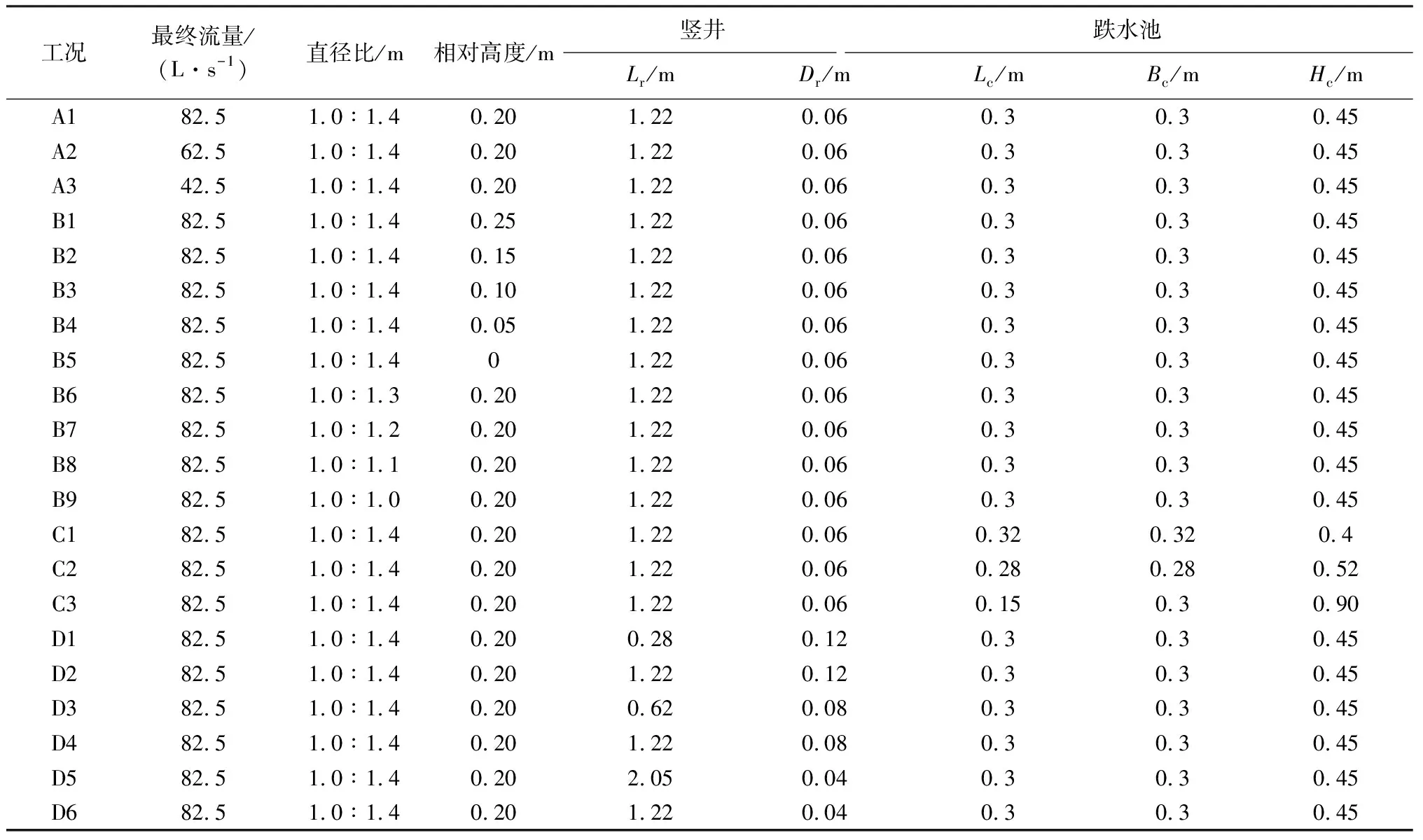
表1 模拟工况

2 模拟结果与分析

2.1 试验数据与模拟数据对比

系列A的3种工况下，管道系统中的流量由20.0 L/s的初始流量分别快速增加到82.5 L/s、62.5 L/s和42.5 L/s的最终流量，模拟压力与Liu等[12]的试验压力对比如图3所示。当最终流量为82.5 L/s时，跌水池底部最大模拟压力为33.5 kPa，相比于Liu等[12]试验结果的33.2 kPa增大了1.0 %，且模拟压力及试验压力均经过3个震荡周期后达到了稳定，说明模型在模拟最大井喷压力时具有良好的精度。当最终流量分别为62.5 L/s和42.5 L/s时，模拟压力与试验压力的差值分别为5.5%和3.5%。流量较小时，试验压力波动较大，对数值模拟结果的精确度带来了一定的影响。因此，本文竖井及跌水池参数特性的研究均选用82.5 L/s的最终流量。

图3 跌水池底部模拟压力与试验数据对比

2.2 上下游管道布设及体形参数的影响

由于上下游管道相对高度导致快速填充水流折返后截留气团在跌水池中，因此工况B系列针对不同上下游管道相对高度进行研究。通过控制上游管道与跌水池的连接高度，对不同上下游管道相对高度进行研究。上下游管道的直径分别为0.20 m和0.28 m，管道直径比为1.0∶1.4。相对高度分别选取为0.25 m、0.20 m、0.15 m、0.10 m、0.05 m和0 m。不同工况条件下管道及跌水池内水的体积分数变化如图4所示。在初始条件下下游管道均为有压流动。随着上下游管道高度差的降低，初始流量在使下游管道填充成有压流动的同时，上游管道内的水流流态逐渐从明渠流过渡成有压流动。当上下游管道顶部高度一致后，继续降低上游管道的高度对跌水池内水位影响较小。

图4 不同上下游管道相对高度下跌水池内水的体积分数变化

当相对高度为0.20 m时，管道及跌水池内水的体积分数变化如图4(b)所示。快速填充的水流沿着上游管道向跌水池移动，在t=1.75 s时撞击跌水池壁后折返进入竖井，将气体截留在跌水池及竖井中。水流继续流入压缩截留气团，在气体压力推动下竖井内的水柱向上移动。压力在t=1.94 s达到最大，其值为33.5 kPa。随后水柱在t=1.97 s被喷出竖井，发生井喷，最大井喷高度约为1.96 m(以跌水池底部作为0点)。随着水流继续流入，井喷再次发生，但强度弱于第一次井喷。跌水池内的气体在t=4.75 s时基本被排出，此时井喷过程结束，管道内的水流达到相对稳定的状态。当上下游管道相对高度为0 m时管道及跌水池内水的体积分数变化如图4(c)所示。跌水池底部的压力在t=0.30 s达到最大，竖井中的水柱在t=0.38 s时被喷射出竖井，发生井喷。最大井喷高度约为2.52 m。工况B系列的数值模拟结果见表2。

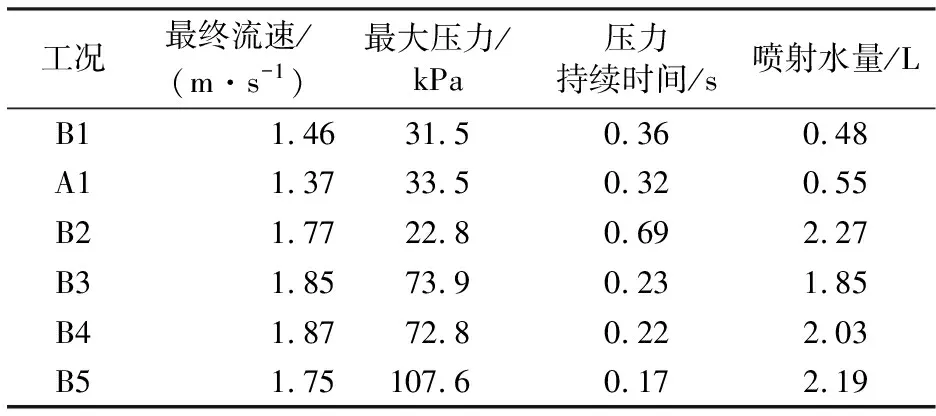
表2 工况B系列及A1模拟结果

下游管道水流速度的提升来源于跌水池内高压的驱动及上游入流动量的传递。当上下游管道相对高度较小时，上游管道为满管流。上游管道流量的突然快速增加，导致跌水池内的水位瞬时急剧上升。由于此过程中参与相互作用的气体较少，井喷过程中发生的压力类似于水锤压力，水气混合物喷出后跌水池内压力迅速降低。此过程压力的持续时间为0.17 s，持续时间较短，但产生的压力峰值达到了107.6 kPa，如图5(a)及表2所示。当上下游管道相对高度为0.15 m时，上游管道截留了部分气团，在管道快速填充过程中气团发挥气垫作用，降低了最大井喷压力，增加了压力的持续时间。如图5(b)所示，由于压力峰值的降低，从竖井中喷射出的水量也相应减少。随着相对高度差增大，上游管道内水流流态在初始状态下变为明渠流。井喷过程中有较多的气体被截留在管道中，此部分气体发挥了缓冲作用，因而井喷过程中的压力峰值降低。

图5 不同上下游管道相对高度压力和喷射水量

下游管道直径的大小影响排水系统的输运能力，进而影响到井喷过程中快速增加水流的释放。由图6可知，随着下游管道直径的减小，管道中的压力峰值和井喷期间喷射水量呈上升趋势：当上下游管道直径比分别为1.0∶1.4、1.0∶1.2和1.0∶1.0时，压力峰值分别为33.5 kPa、63.1 kPa和100.8 kPa，喷射水量分别为0.55 L、1.51 L和3.24 L。Liu等[20]对上下游管径比为1.0∶1.0的工况进行了研究，由于初始条件的跌水池和上游管道中较多的气体起到了缓冲作用，产生了相比本文中上下游管道直径相同时较小的压力峰值。下游管道直径越大，管道的输运能力越强，因而上游管道快速填充的同时可以排出更多的水流以缓解井喷压力，从而竖井喷射出的水量减小。

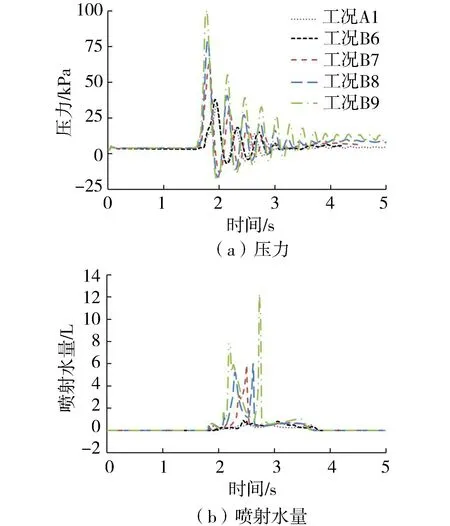
图6 不同上下游管道直径比下压力和喷射水量变化

2.3 跌水池体形参数的影响

初始状态下跌水池内气体占据的空间可供井喷过程中水气发生相互作用。空间越大，水气相互作用越充分，因而产生的压力峰值越小。当跌水池总体积相同时，底部断面面积越小，跌水池的高度越高。在初始水位相同时，较高的跌水池内气体占据的空间更大。本节研究了跌水池体积不变情况下“瘦长形”和“矮胖形”跌水池模型中的井喷过程。工况A1和3种改变体形的跌水池形状和初始流量下的水体积分数如图7(a)所示。图7(b)(c)给出了不同尺寸跌水池的压力和喷射水量变化。当跌水池的高度分别为0.45 m和0.40 m时，“矮胖形”模型相比于工况A1，压力峰值增大了20.8%；当跌水池的高度分别为0.45 m和0.52 m时，“瘦高形”跌水池相比于Liu等[12]试验模型，跌水池底部的压力峰值减小了9.0%；当减少跌水池长度，进一步增加排水池的高度到0.90 m时，压力峰值减小了72.7%。增加跌水池高度，会增大跌水池上方气体空间，进而减少管道中的压力峰值。工况A1喷射总水量为0.55 L，“瘦高形”跌水池的喷射总水量分别为0.62 L和0.53 L，“矮胖形”模型中喷射总水量为0.60 L。提高跌水池高度可以缓解井喷峰值压力，对喷射水量的影响较小。

图7 不同尺寸跌水池中水体积分数、压力和喷射水量变化

2.4 竖井体形参数的影响

井喷过程中竖井中水柱在气团作用下被喷出竖井，最终的喷射高度与水柱本身的特性、气团压力相关。竖井内水柱体形受竖井直径的影响，气团的推动时间受竖井长度的影响。工况D1、D3和D5中的竖井体积与工况A1相同，主要研究竖井在输送水量和空气体积相同的情况下，不同竖井长度对管道中压力的影响；工况D2、D4和D6中的竖井长度与工况A1相同，主要研究竖井直径对井喷强度的影响。数值模拟的压力和喷射水量变化如图8所示。

图8 不同尺寸竖井下的井喷压力和喷射水量

由图8(a)(b)可以看出，当竖井直径相同时，改变竖井长度对井喷压力的影响较小：当竖井直径为0.12 m时，长度分别为0.28 m和1.22 m时产生的井喷压力分别为21.9 kPa和23.6 kPa，增大了7.8%。这是由于在t=1.83 s时气团的压力已经达到最大，而此时水柱的高度为1.13 m，气团对水柱的加速过程已经结束，因而继续增加竖井长度不会产生更大的压力。当竖井长度相同时，增大竖井直径导致压力峰值逐渐增大：当竖井长度为1.22 m，直径分别为0.08 m、0.06 m和0.04 m时，井喷压力分别为34.6 kPa、33.5 kPa和18.7 kPa。但随着直径的进一步增大，竖井对水流的限制作用降低。此时竖井相当于另一条管道，增大了输运能力，因而最大井喷压力降低：当竖井直径为0.12 m时，最大井喷压力为23.6 kPa。

由图8(c)可以看出，当竖井直径为0.12 m，长度分别为0.28 m和1.22 m时产生的喷射水量分别为12.29 L和0.90 L，减少了92.7%；当竖井直径为0.08 m，长度分别为0.62 m和1.22 m时产生的喷射水量分别为3.25 L和0.90 L，减少了72.3%。增加竖井的长度可以减少喷射水量。当竖井长度为1.22 m时，直径分别为0.08 m、0.06 m和0.04 m时产生的喷射水量分别为0.90 L、0.55 L和0.25 L。减小竖井直径可以限制水流的喷射，但会导致气团被滞留在水池中，进入下游管道，威胁后续竖井的安全。

3 结 论

a.当上下游管道直径比小于1时(即下游管道直径大于上游管道直径)，较小的上下游管道相对高度会导致初始状态下上游管道内的流态为满管流动，井喷过程中产生较大的井喷压力；减小下游管道直径将会限制进入下游管道的水流流量，进而造成更为严重的井喷事件。

b.在控制总体积不变情况下增加跌水池的高度能够在一定程度上缓解井喷压力，压力峰值能够减少72.7%。

c.增加竖井的长度不能降低井喷过程中的最大压力，但会减少喷射水量，相较于长度为0.28 m的竖井，长度为1.22 m竖井中的喷射水量减少了92.7%；井喷压力随着竖井直径的增加先增大后减小。