降雨入渗条件下兰溪市某防洪古城墙稳定性分析

董志勇，庞鑫杰，周建芬

(1.浙江工业大学土木工程学院，浙江 杭州 310023；2.浙江水利水电学院水利与环境工程学院，浙江 杭州 310018)

兰溪古城墙沿兰江修建，始建于北宋，经历了多次修复和重建，于2017年被列为浙江省省级文物保护对象。该城墙担负着老城区的防洪安全重任，同时也是当地重要的人文景观。在梅汛期和台汛期，由于连绵阴雨或大暴雨的作用，古城墙存在安全稳定性问题。如2017年洪水期间，古城墙出现多处冒水、管涌等现象，且部分坍塌，洪水灌入兰溪老城，导致城区被淹，约10万人受灾。

目前，计算流体力学和计算固体力学的快速发展实现了渗流场与应力场耦合。土体渗流与应力耦合理论最早是根据多孔介质的力学特征描述的[1-2]。太沙基(Terzaghi)和比奥(Biot)是多孔介质中耦合问题研究的理论奠基者。20世纪初，太沙基提出了有效应力原理、一维固结理论，并进一步扩展到三维，建立了太沙基-伦杜立克方程，为土力学中渗流场与应力场的耦合奠定了理论基础。比奥推导出三维流固耦合方程，建立了土体骨架变形与孔隙水压力之间的关系，并在求解过程中直接体现了渗流场与应力场的相互作用[3]。但是比奥固结理论设计参数较多，难以准确测得，且得出方程的解析解也较困难。因此，在一段时间内比奥固结方程没有在工程中得到广泛应用。随着现代计算技术的发展，尤其是有限元法的发展，比奥固结理论才得以应用于工程实践中。国外，Noorishad等[4-5]提出了裂隙渗流与应力的耦合分析模型；Asaolollahi等[6]在冻土地区隧道涌水问题中，考虑了渗流场、应力场以及温度场三场之间的相互作用，并探究了在三场耦合作用下隧道的稳定性问题。国内，平扬等[7]以比奥固结理论为基础，研究在开挖过程中渗流场与应力场的变化规律及其对基坑稳定的影响。王媛[8]根据比奥固结理论、伽辽金有限元法，联立了渗流与应力方程，建立了以位移和孔隙水压力为未知量的方程，可以同时计算出渗流场与应力场，并以重力坝为例验证了该方法和计算程序的可行性。柴军瑞等[9]从均质土坝的渗透特性出发，分析了均质土坝渗流场与应力场相互作用的力学机制，提出了均质土坝渗流场与应力场间接耦合分析的连续介质数学模型，并讨论了该数学模型的有限元数值解法。

国内外学者的广泛关注和研究，推动了渗流-应力耦合理论的应用和发展。与此同时，边坡渗流稳定分析也得到了迅速发展。毛昶熙等[10]用土体单元所受的渗透力替代土条周边的孔隙水压力，从而开辟了新的分析土坡稳定性的途径。这种方法考虑了渗流场与应力场的相互作用，从而提高了稳定性分析的精度，并在几个实际工程中得到了理想的结果。随后，黄俊等[11]提出用土条所受的渗透力代替孔隙水压力的边坡稳定计算方法，在实际工程中得到了较好的结果。汪自力等[12]在有限元计算基础上，也用土体单元所受的渗透力代替其周边的孔隙水压力，采用数学规划中的单纯形法自动寻找最小安全系数；李吉庆等[13]以极限平衡理论为基础，对比分析了毕肖普条分法和有限元单元法，指出了条分法在计算渗流作用下边坡安全系数时存在的缺点，并论证了以土条受到的渗透力来代替土条边界水压力的有限元单元法的优越性，并通过模型土坝及几个实例土坝加以验证；徐卫亚等[14]综述了国内外降雨型堆积体滑坡渗流稳定性研究进展，并对今后研究作了展望；刘永涛等[15]结合EEMD和RVM算法的优点，构建了土石坝渗流量时间序列的预测模型，为土石坝渗流分析提供了新的方法。在研究非饱和土方面，张信贵等[16]根据饱和与非饱和土体抗剪强度及渗流特性，推导了饱和与非饱和土体在应力场和渗流场耦合作用下的有限元方程。韦立德等[17]建立一个考虑饱和与非饱和渗流场与应力场耦合的三维强度折减有限元模型。张玉军等[18-20]通过推导非饱和土中渗流与应力耦合有关的方程获得解析解。田东方等[21]阐述了坡面径流-非饱和渗流场与应力场耦合的重要意义和作用，提出了渗流场与应力场间接耦合的计算方法。

随着有限元商业软件的发展，许多学者利用ABAQUS、FLAC3D、GEO-SLOPE、PLAXIS、北京理正等研究边坡稳定性问题。徐海奔[22]利用ABAQUS有限元软件对饱和与非饱和渗流规律进行了初步探讨。唐晓松等[23-25]通过PLAXIS、ADINA等有限元软件对渗流作用下的边坡稳定性进行了分析，并利用GEO-SLOPE程序进行验算；Desai等[26-27]利用有限元软件模拟库水位骤降下边坡的稳定性。综上，虽然国内外学者对渗流场与应力场耦合分析研究较多，但在实际加固设计中考虑较少，尤其是耦合作用对挡土墙稳定性的影响。本文在降雨入渗条件下，基于ABAQUS软件，对兰溪市某防洪古城墙边坡措施的渗流场和应力场进行数值模拟，比较分析了不同加固措施对古城墙稳定性的影响。

1 数值模拟方法

边坡内渗流场与应力场的相互作用、相互影响较为复杂。一方面，渗流场会因外界条件的改变而变化，致使土体孔隙水压力分布发生变化，从而导致土体和作用在土体上的有效应力与渗透力发生变化，即改变了应力场；另一方面，应力场的变化会导致土体发生变形，从而改变土体的孔隙率和渗透系数，即改变了渗流场。

1.1 流固耦合分析的基本原理

由于岩土体的孔隙结构比较复杂，通常把流体和固体看作一个理想的连续体，用这个连续体代替复杂的孔隙结构，建立渗流与应力耦合的控制方程。ABAQUS软件控制方程就是基于连续介质的概念将多孔介质分为固相和液相。固相应力平衡可用虚功原理表示：

(1)

式中：σ为有效应力；δε为虚变形速率；δv为虚速度场；T为单位面积的表面力；f为体积力(不包括流体质量)；s为固相的饱和度；n为固相材料的孔隙率；ρw为流体密度；g为重力加速度。

应用有限元法的位移模式和拉格朗日公式可以将虚功方程离散化，得到固相的有限元网格，并使液相通过网格。流体必须满足连续性方程，使得某时段流入或流出的流量等于流体体积的变化率，渗流连续性方程为

(2)

式中：ρe为流体的参考密度；vf为渗流速度；n为S面外法线方向。

式(2)应用了反向欧拉法得到近似积分，将孔隙水压力看作一个变量，并对其进行有限元离散。另外，孔隙内流体遵循2个定律，分别在不同条件下采用：一是Darcy定律，用于流速较低的情况；二是Forchheimer定律，用于流速较高的情况。

1.2 降雨入渗边界条件处理

降雨入渗随时间和空间变化，通常用土体允许入渗容量fp、土体饱和渗透系数ks和降水强度q这3个因素之间的关系描述降雨入渗模型[28]。3种不同情况如下：①当q≤ks时，降雨全部渗入土壤，地表不发生径流；②当fp>q>ks时，雨水全部入渗，fp随着入渗深度的增加呈递减趋势，但这个阶段不会发生径流；③当q≥fp时，雨水不能全部入渗到土壤中，所以会产生径流。

本文在模拟整个降雨过程中，默认入渗率大于降水强度，将降水强度设置为流量边界，从而模拟入渗问题。

1.3 墙体与土体接触和渗流计算

1.3.1接触模拟

采用ABAQUS软件中的相互作用模块，在该模块中设置挡土墙与土体的接触面，包含接触面的法向作用和切向作用。其中，接触面的法向模型采用硬接触，即两物体只有在相互压紧的状态下才能传递法向压力，若两物体之间有间隙则不能传递法向压力；接触面的切向作用考虑为无摩擦，即默认古城墙的墙背光滑。

1.3.2渗流模拟

当接触界面两侧都存在孔压自由度时，则计算的接触压力为有效压力，即不考虑孔隙水压力的影响。如果接触界面只有一侧包含孔压自由度，则不会出现流体流入或穿过接触界面的现象，在这种情况下，接触压力是总压力，即考虑孔隙水压力的影响。

1.4 挡土墙稳定性计算

根据《水工挡土墙设计规范》，抗倾覆稳定安全系数K的计算公式为

(3)

式中∑Mv、∑MH分别为对挡土墙基底前趾的抗倾覆力矩和倾覆力矩。

2 古城墙渗流分析

2.1 古城墙概况

兰溪市某古城墙是兰江防洪堤的一部分，其断面为梯形，高6 m，顶宽0.6 m，底宽1.2 m，墙后土体为砂性土，地基为不透水岩基，横断面如图1所示。墙后土体的材料属性：干密度为1 400 kg/m3，黏聚力为5 kPa，有效内摩角为25 °，弹性模量为100 MPa，泊松比为0.32，饱和渗透系数为1.354 m/h，初始孔隙比为1.0。古城墙体的材料属性：密度为2 400 kg/m3，弹性模量为2 000 MPa，黏聚力为260 kPa，有效内摩角为51°，泊松比为0.1，饱和渗透系数为0.02 m/d。由于地基为不透水岩基，因此不考虑地基对古城墙的影响。边界条件设置：模型右侧边界施加水平方向位移约束，边坡底部为全约束边界和不透水边界。接触设置：古城墙与土体采用面面接触，接触面法向模拟采用硬接触，并设置摩擦系数为0.3。古城墙体和土体采用本构模型和屈服准则，分别为理想弹塑性本构模型和Mohr-Coulomb强度准则；选用CPE6M六结点修正二次平面应变三角形单元，计算网格布置如图2所示。

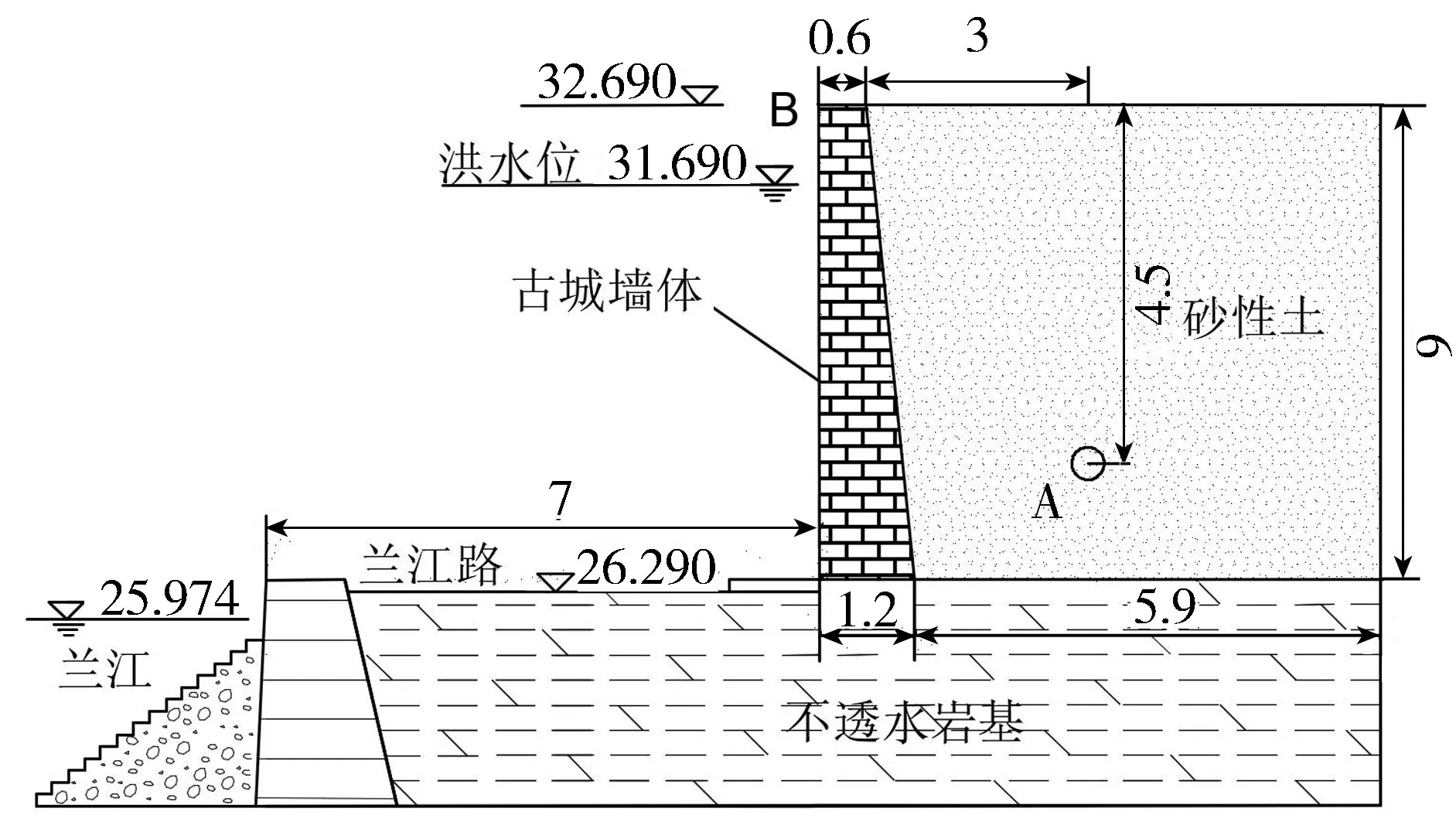
图1 古城墙横断面(单位：m)

图2 有限元模型的计算网格

2.2 土压力计算分析

图3中黑色实心圆表示由土压力计测得的离地面4.5 m、离古城墙墙顶3 m处土压力。由图3可知，ABAQUS模拟值在深度小于1 m时土压力为零，在深度大于1 m时土压力随着深度的增加而增大，呈三角形分布，符合土力学理论。土压力计的实测值与ABAQUS模拟值接近，而库伦理论值偏大，这主要因为理论计算没有考虑黏聚力对土的影响，且忽略了墙体与填土之间相互作用以及位移协调作用。因此，基于ABAQUS软件对降雨入渗条件下古城墙墙后土体孔隙水压力和墙体稳定性进行模拟是可行的。

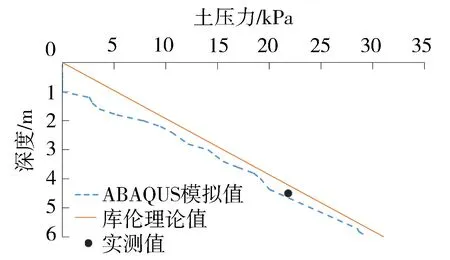
图3 水平应力随深度的变化

2.3 有倒挂井的古城墙孔隙水压力变化过程

在边坡除险加固中，用倒挂井作为防渗处理设施，可减少大量的土石方开挖，且防渗效果好。本文对古城墙采用倒挂井联合支护的方式，截断堤身的渗流通道，并探究古城墙孔隙水压力变化过程。有防渗设施的古城墙横断面如图4所示，倒挂井直径为1.6 m，深度约为6 m，倒挂井井壁材料为拱顶及拱座倒挂筋，井内回填C25W6F50砼，古城墙与倒挂井通过每间隔6 m设置一道混凝土拉梁进行连接。倒挂井的材料属性：密度为2 400 kg/m3，弹性模量为20 GPa，泊松比为0.25，饱和渗透系数为0.01 m/d。数值模拟中需计算模型所有节点的应力、位移、孔隙水压力、流速以及接触应力。

图4 有倒挂井的古城墙横断面(单位：m)

为了探究有倒挂井的古城墙孔隙水压力变化过程，采用瞬态方式进行降雨入渗全过程的渗流场与应力场耦合分析，边坡顶部为流量边界，雨水入渗强度为1 354 mm/h，历时24 h，倒挂井与土体、土体与古城墙的连接选用面面接触。有倒挂井的古城墙孔隙水压力遭遇降雨历时的等值线如图5所示。为了能准确定位浸润线，将孔隙水压力为负值的区域设置为灰色，即蓝色等值线以上的区域，则孔隙水压力为0的等值线就是浸润线。与此同时，也能更好地区分饱和区与非饱和区。由图5可知，随着降雨历时的增加，孔隙水压力不断增大，浸润线逐渐升高，古城墙后土体的饱和区域不断扩大，非饱和区域不断缩小，直至第5小时，土体达到饱和状态，雨水不能入渗到土体中，以致发生地表径流。

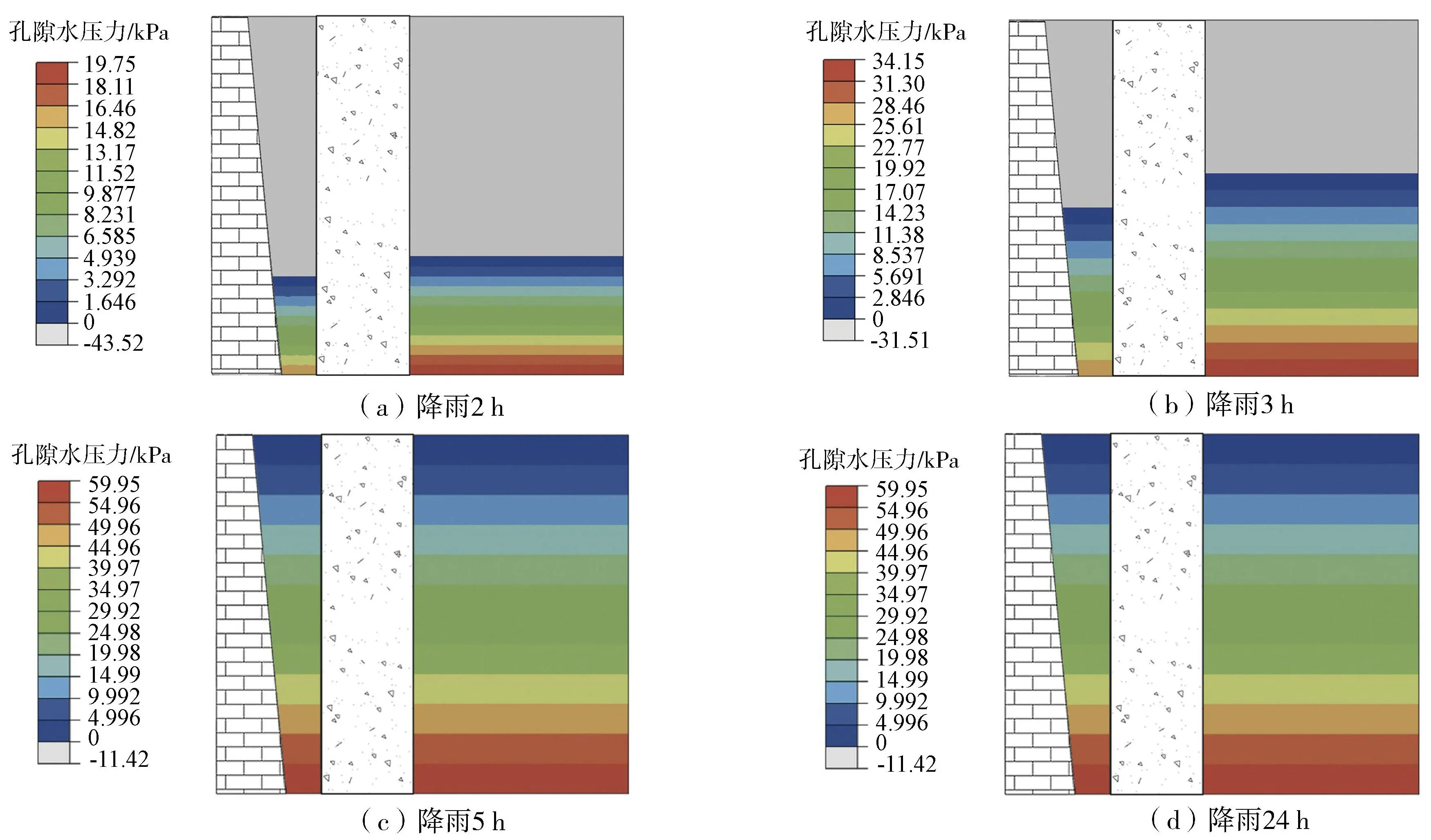
图5 有倒挂井的古城墙墙背孔隙水压力等值线

3 具有排水设施的古城墙降雨渗流分析

反滤层常用于坝基、坝体、重力式码头和板桩码头中，可以防止土颗粒随渗流析出，并且能保证渗流顺畅，以达到排水减压的效果。本节采用反滤层加排水管以降低孔隙水压力，并分析在有、无排水设施情况下，古城墙孔隙水压力和流速的变化过程。具有排水设施的古城墙如图6所示，反滤层从内向外由直径0.5～1.5 mm的砂粒、直径5～25 mm的碎石和直径25～100 mm的碎石组成，渗透系数从内向外分别为0.05 m/d、0.3 m/d和0.8 m/d，排水管设置在距离底部1 m处，直径为50 mm。

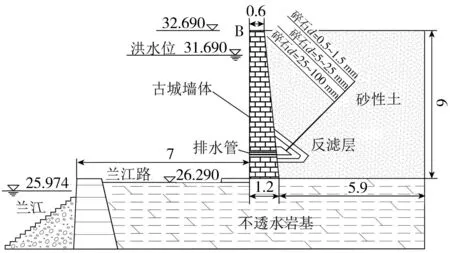
图6 有排水设施的古城墙横断面(单位：m)

3.1 孔隙水压力变化过程

为了探究有排水设施的古城墙孔隙水压力变化过程，采用瞬态方式进行降雨入渗全过程的渗流场与应力场耦合模拟，边坡顶部为流量边界，雨水入渗强度为1 354 mm/h，历时24 h，计算中土体与古城墙的连接选用面面接触。由图7可见，在墙后水位到达排水管处之前，孔隙水压力增长趋势较快，当水位超过排水管时，孔隙水压力的增长速率和浸润线升高的趋势明显变缓，墙后水流不断被排出。

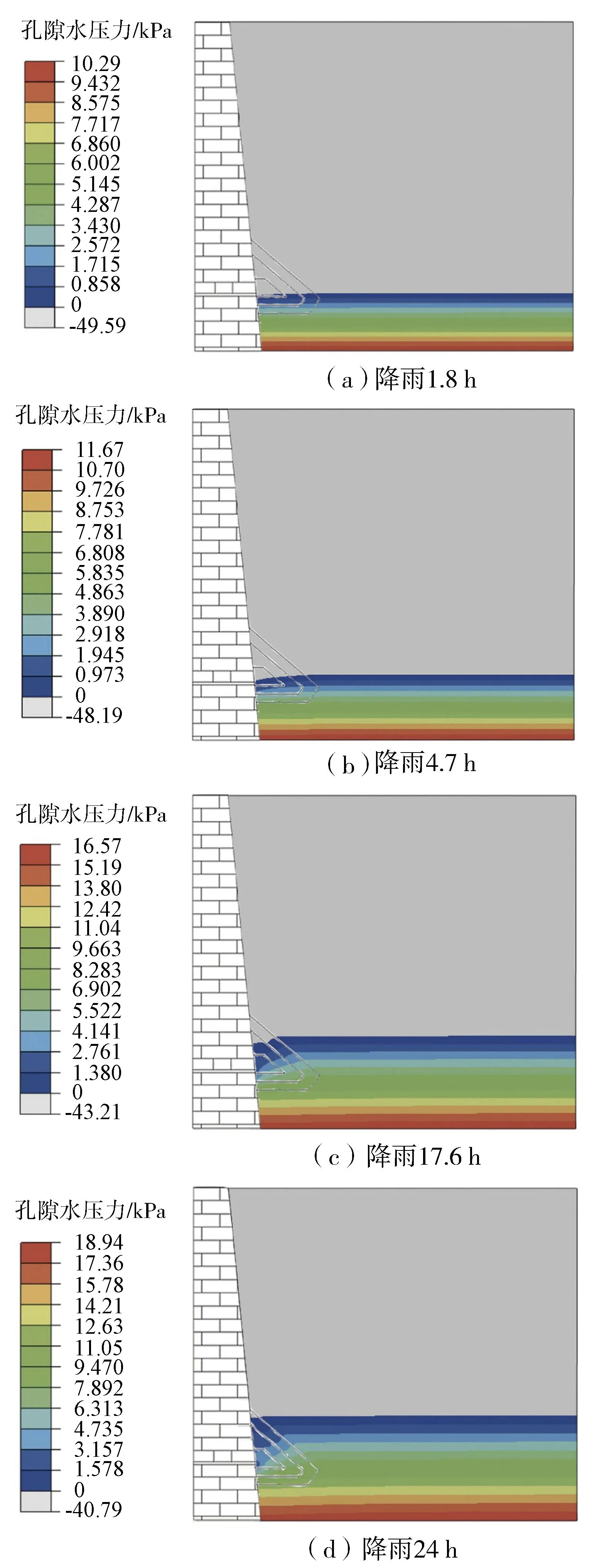
图7 有排水设施的古城墙墙背孔隙水压力等值线

3.2 排水设施对渗流场的影响

为了更好地分析排水设施对古城墙后渗流场的影响，在相同计算条件下，对无排水设施的古城墙进行了降雨渗流分析，并将2种情况的计算结果作了比较。对比图7(d)和图8可知，由于没有排水设施，墙后的地下水无法排出，在经历相同的降雨历时后，无排水设施的古城墙土体的孔隙水压力远大于具有排水设施情形。

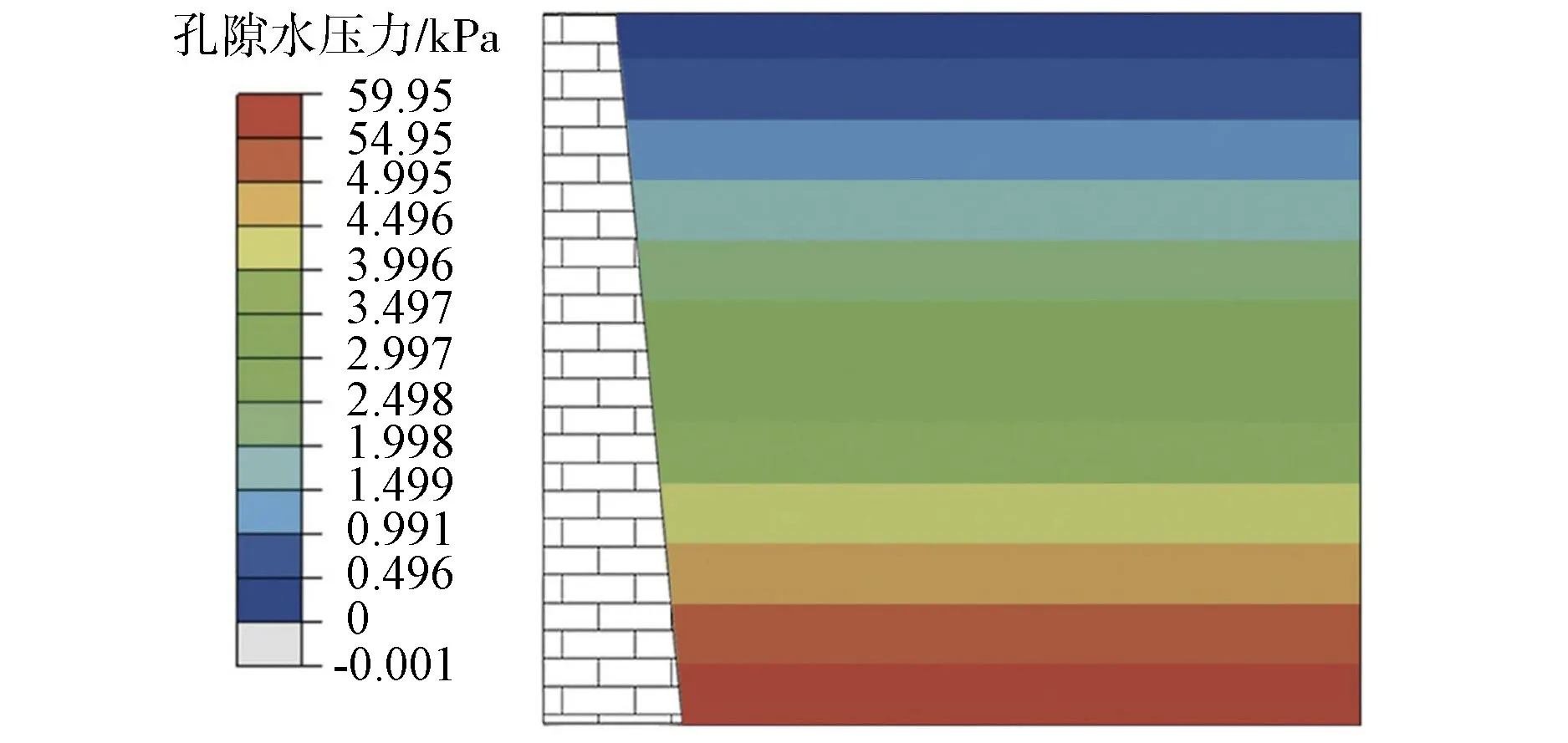
图8 持续降雨24 h后无排水设施古城墙孔隙水压力

由图9可见，降雨渗流可通过排水管排出，从而形成渗流通道，而无排水设施的古城墙因土体已处于饱和状态以致于后续的降雨渗流溢出。

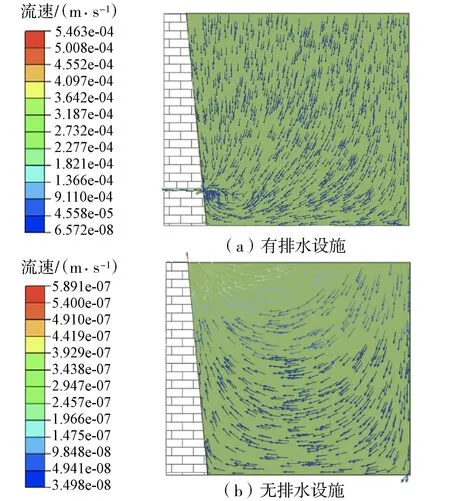
图9 降雨24 h后古城墙流速矢量比较

4 古城墙稳定性分析

4.1 古城墙抗倾稳定性分析

在有排水设施、无排水设施和倒挂井3种情形下，降雨24 h后的古城墙接触应力与深度的关系如图10所示。从图10中可以看出，不同情形接触应力随深度变化的规律基本一致，随深度的增加而增大，近似呈三角形分布，但三者在数值上存在差异，尤其与有排水设施差异较大。有排水设施的古城墙后的地下水位比其他2种情形都低，其对古城墙的应力也都小于另外2种情形。另外，倒挂井是采用“堵”水的方式，在计算结果上与无排水设施情形相近。

由表1可知，由于排水设施的存在，墙后孔隙水压力对古城墙的压力大幅度减小，相比其他2种情形，有排水设施古城墙受到的总压力和倾覆力矩最小，也是最稳定和最安全的。有倒挂井情形，墙背所受的压力和倾覆力矩都有所减小，但是效果并不明显，因此，设倒挂井并不能有效提高古城墙的稳定性。

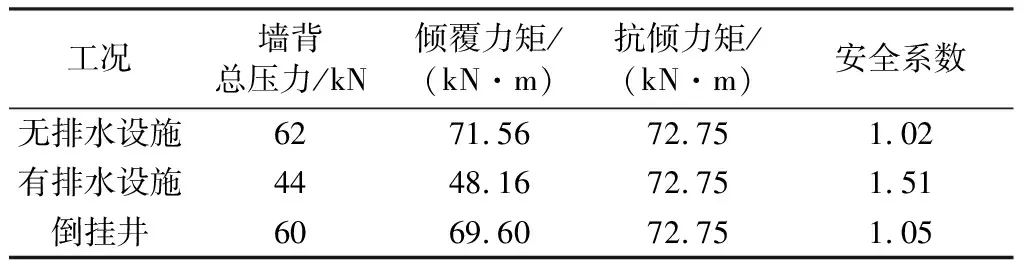
表1 降雨24 h后古城墙抗倾稳定性

4.2 古城墙抗滑稳定性分析

由图11可见，2 h时有、无排水设施B点水平位移增长的量级是相同的，是线性增长，但有倒挂井的增长缓慢，主要是因为倒挂井的消减土压力作用。无排水设施和有倒挂井情形古城墙B点(图1)水平位移先随时间增加而增大，而后趋于平缓。这是由于在降雨5 h后，墙后地下水位已上升至墙顶，墙后土体处于饱和状态，其孔隙水压力和土压力将一直保持不变。而具有排水设施的墙后地下水在降雨2 h后位于排水管处，因此可看出有排水设施城墙B点位移起初呈快速增长的趋势，但在2 h后变得缓慢。比较3种情形的B点水平位移，由于无排水设施和有倒挂井情形无排水通道，地下水无法及时排出，墙体所受压力较大，因此B点水平位移均比有排水设施情形大。

图11 不同情形古城墙B点水平位移随时间的变化

5 结 论

古城墙无排水设施时，历经24 h降雨后，墙后孔隙水压力增大，致使墙背所受压力增大，降低了古城墙的稳定性；有排水设施时，墙后孔隙水压力大幅度减小，增强了古城墙的稳定性；有防渗设施时，墙背所受压力并不能有效降低，安全系数未明显增大。