基于扰动观测器的双馈风电机组最优复合反馈控制研究

吴晓月，王 冰，陈玉全，程明曦，曹智杰

(1.河海大学 能源与电气学院，南京 211100；2.南京豪庆信息科技有限公司，南京 210006)

0 引 言

随着新能源发电的不断发展，风能作为一种易获得、无污染的清洁能源越来越受到各国的欢迎[1]。截止至2020年底，全球风电累计装机容量已达到743GW，中国风电累计装机容量已经突破288GW[2]。随着风电装机增加，为了保证电网和风力发电系统的稳定性，仍有很多问题需要解决，比如，风速的不确定性问题、外部干扰问题、风电并网的高/低电压穿越问题、系统中电力电子元件产生的谐波问题等[3-4]。

目前，对谐波扰动研究的文献相对较少。双馈风电机组在运行过程中，大量的电力电子器件处于工作状态，因此需要对双馈风电机组可能产生的谐波进行考虑。文献[5]采用内模控制原理对风电机组受非谐波干扰问题进行了控制研究，但是该方法只能解决一种具体的扰动问题。文献[6]主要是对大规模双馈风电机组并网使得电网产生的谐波电流进行控制，并未考虑双馈风电机组在运行过程中可能产生的谐波进行分析。文献[7]通过对风机谐波特性进行分析，提出了一种谐波责任划分方法；但是该方法中风机的谐波特性需要根据实测数据来分析。文献[8]针对风电机组容易受电网中谐波分量影响的问题，采用基于重复控制的直接功率控制策略，同时消除了风电系统的谐波分量；但该控制策略的实现是以牺牲控制系统动态性能为代价。

双馈风电机组中含有双馈变流器，双馈变流器的引入使得双馈风电机组输出的电流中含有大量的谐波，这会使双馈风机输出有功功率输出不平稳，可能会影响电网的稳定性。考虑到这种谐波对双馈风电机组造成的影响，设计了一种基于扰动观测器的最优复合反馈控制策略。其中最优复合反馈控制主要是保证风机系统在理想状态下的有功功率的稳定性，扰动观测器是用来观测系统的谐波扰动，以便于在输入端抵消系统谐波扰动的影响；并通过仿真验证了当系统在受到谐波干扰时，所设计的控制策略能够使双馈风电机组有功功率输出稳定。

1 双馈风电机组模型

双馈风电机组的系统模型可以用下面的三阶模型[9]进行描述，包括一阶动力学模型和二阶双馈感应发电机模型：

(1)

由双馈风电机组数学模型可知，动力学一阶模型中不包含控制输入若直接对该模型设计控制策略，很难实现对转差率的控制，这时所设计的控制器往往只能使转差率稳定在设置的初始值的位置，而非其真正的平衡位置。为解决这个问题，通过坐标变换，消去动力学方程中的常数项，使设计的控制器在保证感应发电机稳定的同时，也能使转差率保持在稳定状态。令：

(2)

式中，s为转子转差率，Eq和Ed分别为在瞬态电抗下的q轴和d轴电压。坐标变换后，双馈风电机组的模型就变换成式(3)的形式，之后在该变换模型的基础上对双馈风电机组进行控制器的设计。

(3)

2 双馈风电机组控制器设计

相对于线性系统，非线性系统的控制往往是比较复杂的，这时如何用线性控制理论来解决非线性控制问题是一个重要的问题，反馈线性化[10]就是解决非线性控制的一种有效方法。于是先通过坐标变换改变系统的模型，使用前馈控制抵消系统的非线性项，再采用反馈控制来设计双馈风电机组的控制策略。

2.1 最优复合反馈控制器设计

对双馈风电机组进行控制器设计时，采用的是前馈和反馈结合的一种复合反馈控制，因此设计系统的控制器为

(4)

(5)

然后，采用经典控制理论中的状态反馈控制来设计系统的控制器为

(6)

此时系统的状态方程可以写为

(7)

考虑选取一个积分型泛函[11]J来求得最优的反馈参数值，从而得到最优的反馈控制器。

(8)

式中，Q，R均为正定对称矩阵。

根据极小值原理，当性能泛函J取最小值时有唯一的最优解，这样便可以得到双馈风电机组的最优控制律。

(9)

其中,P为正定对称常数矩阵，且满足Riccati矩阵代数方程[12]：

-PA-ATP+PBR-1BTP-Q=0

(10)

由该等式可以得到P矩阵，进一步得到使系统性能达到最优的反馈控制参数。便可以得到系统的最优复合反馈控制律为

(11)

2.2 稳定性证明

设计双馈风电机组的最优复合反馈控制器，本节主要是用Lyapunov方法证明闭环系统在该最优控制策略下的稳定性。

设计系统(5)的Lyapunov方程为

V=xTPx

式中,P为设计最优控制时的正定对称常数矩阵，故有V>0，对V求导得：

又因为P和R均为正定对称矩阵，且Q=-PA-ATP+PBR-1BTP。故有：

3 扰动观测器的设计

谐波扰动广泛存在于双馈风电机组运行的过程中，谐波的引入会对双馈风电机组控制器的稳定性产生较大影响。谐波扰动的来源可分为电网中的谐波污染以及双馈风机内部电力电子变换器的使用，其中，电力电子器件的使用是主要来源。由于电力电子器件的开关特性，双馈风机的输出电压本质上是畸变的类梯形波，从频域角度来看，输出电压将会夹杂大量高频谐波成分。当系统谐波成分能量过高时，前文建模的双馈风机模型(1)中应当考虑这部分谐波未建模动态。因此，在控制器(9)的基础上进一步设计考虑谐波扰动的双馈风电机组控制器。

滑模控制是一类消除扰动的常用方法[13-14]，但由于滑模切换特性，滑模控制将会造成系统的输出抖振，影响系统运行。因此，本文采用扰动观测器的思想，通过设计双馈风机扰动观测器抵消系统中的谐波扰动、提高系统的谐波抑制能力。

3.1 扰动观测器的设计

因为谐波是正弦波，线性系统可以产生不同频率和幅值的波形[15]，故假设在双馈风电机组变流器处产生的谐波用一个外部线性系统来描述，具体形式如下：

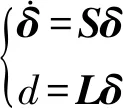
(12)

式中,d即为线性系统产生的谐波扰动。

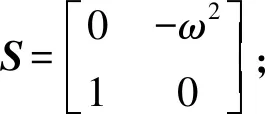
把扰动模型(12)代入到双馈风电机组模型(3)中，可得：

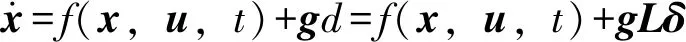
(13)

式中，g是扰动的一个附加增益，可以表示谐波产生的位置和幅值大小。

此时，将系统模型扩展为

(14)

其中状态z与扰动的状态δ具有相同的阶次，p(x)是系统状态的线性方程。

对(14)求导得：

(15)

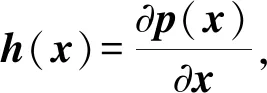
(16)

由此，可以得到扰动的观测值

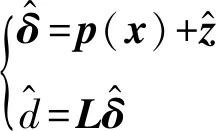
(17)

3.2 p(x)的设计

在观测器设计的过程中，只有先设计出p(x)才能得到扰动的观测值，因此设计观测器最重要的一步就是要确定p(x)。

为确定p(x)，把观测误差渐近于0作为选定p(x)的基准。干扰观测器的动态观测误差为

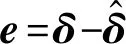
(18)

则有

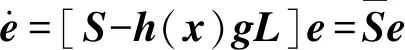
(19)

又因为h(x)=∂p(x)/∂x，因为p(x)是系统状态的线性方程，故通过p(x)的偏导h(x)便可以得到p(x)的确定表达式。

第2节已经设计了双馈风电机组的最优复合反馈控制器，再结合本节的扰动观测器，得到系统的控制框图如图1所示。

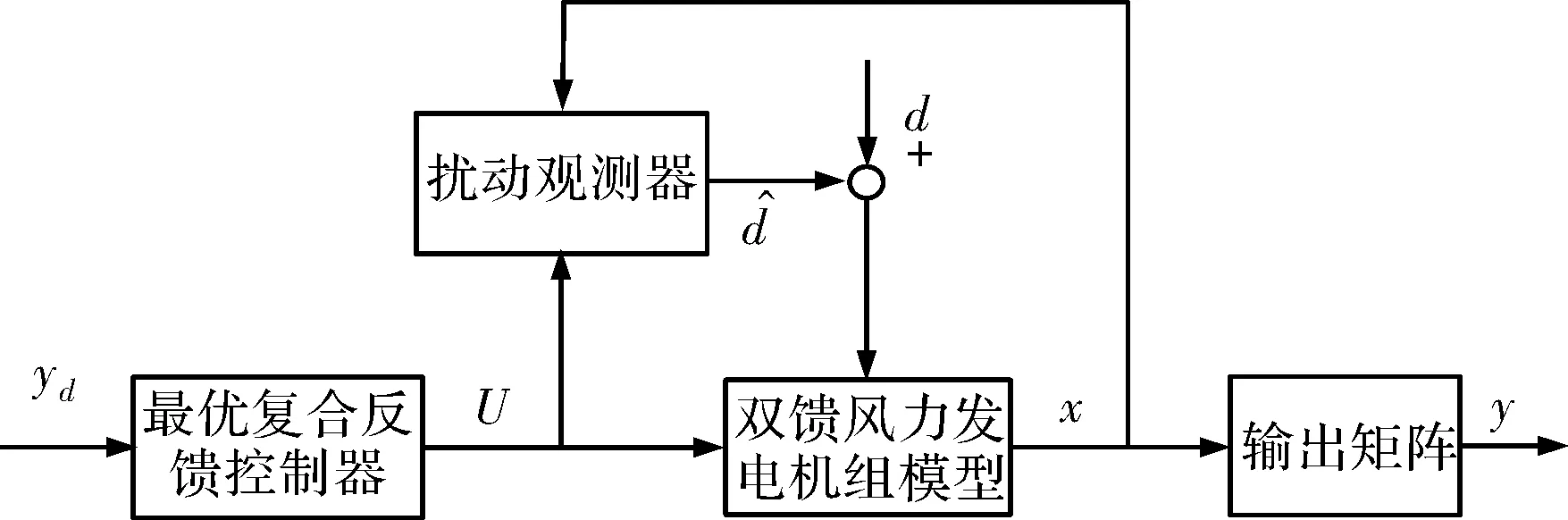
图1 双馈风电机组的控制框图

因此，含扰动观测器的最优复合反馈控制器为：

(20)

4 仿真验证

为了验证设计控制策略的有效性，本节通过Matlab首先对扰动观测器的准确性进行仿真验证，证明了所设计的扰动观测器能够观测出扰动；然后分别对不含谐波扰动、含谐波扰动的双馈风电机组系统进行了仿真，证明了所设计控制策略的有效性。

在对双馈风电机组进行仿真验证时，主要参数设置如表1所示。

表1 双馈风电机组主要参数表

4.1 扰动观测器仿真验证

由式(12)可知，根据矩阵S的维度决定了外部线性系统的阶数，因此在对扰动观测器进行仿真时，分别使用二阶外部系统和三阶外部系统来模拟系统的谐波扰动，并分别对跟踪效果进行了验证。

首先对二阶外部系统产生的谐波进行观测：

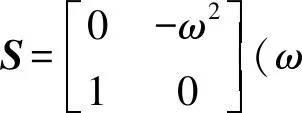
图2 扰动观测曲线

图3 观测误差曲线

下面对三阶外部系统产生的谐波进行观测：

图4 扰动观测曲线

图5 扰动误差曲线

从扰动观测器的观测曲线和观测动态误差曲线可以看出，不管是使用二阶外部系统还是三级外部系统来模拟系统的谐波，所设计的扰动观测器能够准确观测出谐波扰动的值；根据扰动误差曲线可知，外部系统的阶数越高，所设计观测器的观测结果越精确。

4.2 仿真验证

(1)无谐波扰动系统

根据选取的参数，对无扰双馈风电机组进行仿真，双馈风电机组的有功功率输出曲线如图6所示。

图6 无扰动时有功功率输出

从图6可以看出，不管是否为最优反馈参数，只要选择的反馈参数满足系统稳定性的条件，都能使双馈风电机组系统都能到达稳定状态，但与采用复合反馈控制器相比，采用最优复合反馈控制器能够让系统具有更好的动态性能。因此在后续仿真过程中，均使用最优复合反馈控制策略。

(2)谐波扰动系统

因为所设计观测器对三阶外部系统产生的谐波观测精确度更高，因此采用三阶外部系统来模拟系统的谐波扰动。为验证设计的含扰动观测器的最优复合反馈控制器的有效性，在对含谐波扰动系统进行仿真时，把含扰动观测器和不含扰动观测器两种状态进行了对比。得到的有功功率比较仿真曲线如图7所示。

图7 含谐波扰动的有功功率输出曲线

从仿真图可以看出，通过比较受到谐波干扰的系统在加入扰动观测器和不加扰动观测器时双馈风电机组的有功功率输出曲线，可以看出加入观测器的受扰系统可以在有限时间内达到稳定状态，而不加谐波扰动的受扰系统的有功功率输出曲线会随着谐波扰动而振荡。进而证明了双馈风电机组受到的谐波扰动可以从控制输入端得到补偿，也间接验证了所设计扰动观测器的有效性。

5 结 语

针对双馈风电机组中的电力电子器件在风机运行过程中可能产生的谐波干扰，设计了一个含扰动观测器的最优复合反馈控制器。可得到如下结论：

(1)相对于复合反馈控制策略，使用对反馈参数优化后的最优复合反馈控制策略，不仅能够保证系统在理想状态下的稳定性，还使系统具有更好的动态性能。

(2)设计的扰动观测器能够直观、有效的观测出谐波扰动，设计的基于扰动观测器的最优复合反馈控制策略能使受谐波扰动的双馈风电机组在短时间内达到稳定状态。

最后在Matlab仿真平台，验证了控制策略的有效性。

因为不同的电力电子器件产生的谐波干扰是不一样的，需要考虑多种谐波扰动对双馈风电机组运行过程中的影响，因此后续可以从复合谐波扰动的方面进一步研究。