双馈风力发电机网侧变换器的非线性控制策略研究

裴泽伟，朱佳兵，吴文超，刘玉帅

(1.国家能源集团东台海上风电有限责任公司,江苏 东台 224200；2.浙江华东测绘与工程安全技术有限公司，杭州 310014)

0 引 言

由于具备可靠性和经济性两大优势，双馈感应发电机(Doubly Fed Induction Generator，DFIG) 在市场上占据了主导地位[1-2]。DFIG系统是一类集同步发电特性和异步发电特性于一体，可通过定子和转子向电网实现双向馈电的风力发电系统[3]。一般地，DFIG系统主要由风机部分、双馈发电机(DFIG)和“背靠背”变换器等部分构成[4-5]。其中，按照与电网的连接方式来区分，“背靠背”变换器可以划分为网侧变换器 (GSC)和转子侧变换器(RSC)两个部分。由于网侧变换器直接与电网相连，将直流侧从转子侧吸收的有功功率传递至电网。因此，网侧变换器的控制器性能将直接影响网侧电流的动态性能。

为了提升DFIG系统电网电流的动态性能，许多学者提出了网侧变换器的非线性控制策略来解决这一问题。网侧变换器的非线性控制方案主要可以分为以下几类：模型预测控制方案[6-9]、状态反馈线性化控制方案[10-12]、滑模控制方案[13-16]、反步控制方案[17-18]等等。

其中，有限集模型预测控制方案以其易于执行和便于处理约束的优点，已广泛应用于电机驱动和过程控制等领域。这一类控制方案的主要思想是在每一个采样周期内求解有限时域内的开环最优问题。从基本原理上看，这一类控制方案具备较强的鲁棒性且建模方便[6-7]。然而，不足之处在于这一类控制方案的性能对系统参数具有很强的依赖性；此外，有限集模型预测控制方案下的系统开关频率不固定，这也将对的网侧变换器系统产生一定的影响[8-9]。

状态反馈精确线性化是一类线性化控制方案。该方案通过状态坐标的非线性变换和非线性状态反馈将原始非线性系统转换成线性的可控可观系统，然后通过线性控制方法(极点配置法或二次型调节器)设计控制器。相比于传统的近似线性化方法，这一类控制方案可以使得原始非线性系统在更广的范围实现稳定[10-12]。同样的，该方案同样十分依赖于系统参数，当系统参数未知或变化时，该控制器的性能将会受到一定的影响。

进一步地，为了提升DFIG网侧变换器系统的干扰抑制能力，许多研究学者提出了滑模控制方案。尽管传统的滑模控制方案对系统参数和外部干扰具备很好的鲁棒性，但是控制器很容易遭受抖颤的影响[13-16]。这是传统滑模控制器的最大缺点之一。

基于此，本文设计了一种网侧变换器直流电压的二阶滑模控制方案。该控制方案不仅对直流侧电容参数扰动和风机发电功率变化具有极强的鲁棒性，还可以有效地抑制开关函数引起的抖颤。最后仿真实验证实了所设计的二阶滑模非线性控制器的鲁棒性。

1 DFIG网侧变换器数学模型

1.1 DFIG系统结构

如图1所示，DFIG发电系统主要由风机部分、双馈发电机(DFIG)和“背靠背”变换器等部分组成。风机部分由桨叶、轮毂、齿轮箱增速机构、塔架等部分组成。其中，DFIG的定子通过接触器直接与电网相连，而其转子则通过“背靠背”变换器接入电网。“背靠背”变换器主要由机侧变换器、网侧变换器及中间直流电容器构成。机侧变换器用于控制风力发电机转速，完成风能到电能的变换，而网侧变换器用于完成电能从风电系统至电力系统的输送工作。

图1 DFIG系统结构示例图

1.2 DFIG网侧变换器数学模型

依据图1，DFIG网侧变换器的单相等效电路图如图2所示。

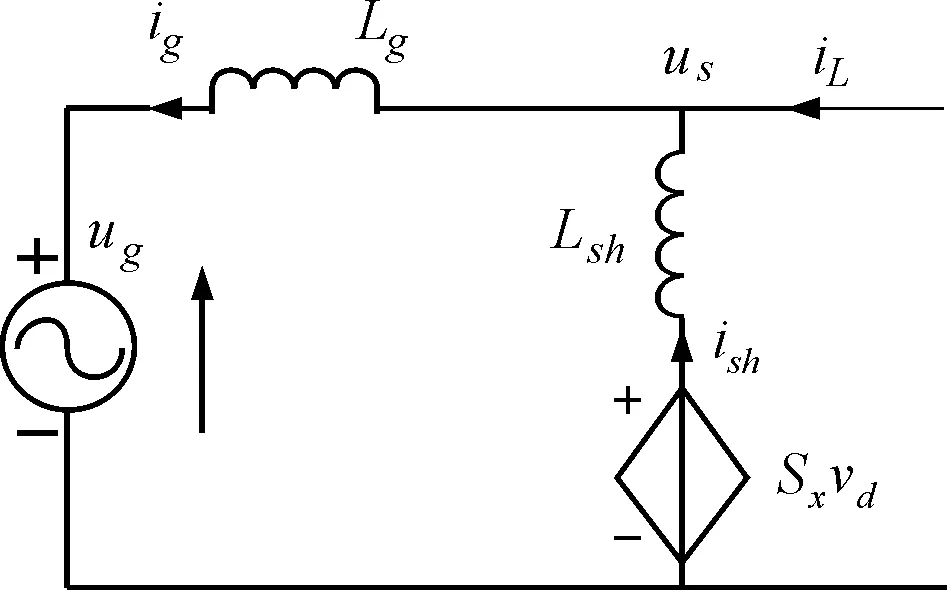
图2 DFIG网侧变换器单相等效电路

依据图2，DFIG网侧变换器在dq坐标系下的数学模型可以写为

(1)

式中，ishd和ishq代表网侧变换器的输出电流的d轴和q轴坐标系下的分量，uod和uoq为网侧变换器的输出交流电压的d轴和q轴坐标系下的分量，usd和usq为DFIG定子侧电压的d轴和q轴坐标系下的分量。Lsh和Rsh代表网侧变换器的滤波器的滤波电感和等效电阻值。

进一步的，依据图1，DFIG网侧变换器的直流侧电压的动态可以写为

(2)

式中，Psh=1.5usdishd;Pse=udidse;idse代表转子侧变换器的直流侧电流;d代表直流侧电容器的电容值。

2 DFIG网侧变换器二阶滑模控制方案

DFIG网侧变换器的控制目标为：将DFIG转子侧的功率稳定地传输至电网和维持直流侧电压的稳定。本文通过采用二阶滑模控制方案来提升直流电压环的动态性能，电流内环采用PI控制方案。DFIG网侧变换器的控制框图如图3所示。

图3 DFIG网侧变换器控制框图

2.1 积分滑模面设计

根据式(2)，DFIG直流侧电压的动态可以重新写为

(3)

依据式(3)，设计直流电压的积分滑模面为，

(4)

2.2 控制率设计

由于具备可以抑制抖震和可以在有限时间内收敛的优点，STA(Super-twisting algorithm, STA)算法已广泛应用于相对阶为1的系统。

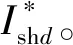
(5)

其中等效控制项可通过求解以下方程来获取，

(6)

将式(3)和式(4)代入式(6)，可以求得等效控制项的表达式为

(7)

STA项可以设计为

(8)

其中，

(9)

式中，ε1d,ε2d代表正常数。sgn(·) 则代表符号函数。

将式(7)和式(8)代入式(5)中，可以求得网侧变换器的输出电流的d轴参考量的表达式为

(10)

2.3 不确定性与鲁棒性

考虑直流母线电容器的电容值误差、变换器的功率损耗及外部扰动，式(3)可重新写为

(11)

其中，

(12)

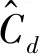
因此，式(11)可进一步写为

(13)

其中，

(14)

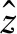
考虑到系统在实际实施过程中的物理约束，可以假定扰动是有界的，也即

|d|<ε

(15)

式中，ε为已知的正常数。

2.4 稳定性

将式(13)代入式(4), 积分滑膜面sd的一阶微分可以重新写为

(16)

因此，将式(10)代入式(16)，闭环系统可以描述为

(17)

为了验证闭环系统的稳定性，设计Lyapunov函数[14]为如下形式，

(18)

其中，

Lyapunov函数V的微分可以得：

(19)

其中，

由于扰动是有界的，依据参考文献[25]，式(19)可以进一步写为

(20)

其中，

(21)

2.5 滑模系数的选取

本文中所设计的直流电压二阶滑模控制器主要包含三个滑模系数：λ、ε1d和ε2d。由公式(4)可以看出，系数λ直接影响闭环系统的动态响应，参数λ越大，系统的收敛时间越短，但是容易引起超调；参数λ越小，系统的收敛时间变长，因此参数λ必须合适的选取。选取参数λ的原理可见参考文献[12]。此外，为了保证所设计的控制器的稳定性，参数ε1d和ε2d的选取需遵循式(21)。

3 仿真结果

为了验证上述所设计的DFIG系统网侧变换器的直流电压的二阶滑模控制方案的有效性与合理性，本小节对DFIG系统进行Matlab/Simulink仿真验证。其中，仿真中DFIG系统所采用的参数如表1所示。此外，DFIG网侧变换器所采用的滤波器的滤波电感Lsh=6 mH以及阻尼电阻Rsh=0.5 Ω，直流电容电压为1.2 kV，额定直流电容为10000 F。仿真中所用到的滑模控制器参数如表2所示。为了便于对比分析，本文采用传统PI控制策略与所提的二阶滑模控制方案进行对比分析，两种不同方案下系统仿真结果如图4～图8所示。

表1 仿真所用DFIG参数

表2 仿真所用的控制参数

图4为所设计的二阶滑模控制方案下DFIG系统在风机功率突增时的仿真波形图。仿真波形主要包括：定子电压us、直流侧电压ud以及电网电流is。由图可知，当风机的发电功率突增时，中间直流侧电压将会波动，并在0.03 ms后稳定。由于发电功率突增，电网电电流幅值也将增大。图5为传统PI控制方案下DFIG系统在风机功率突增时的仿真波形图。由图可知，当风机的发电功率突增时，中间直流侧电压将会波动，并在0.04 ms后稳定。由于发电功率突增，电网电电流幅值也将增大。因此，当风机发电功率变化时，与传统PI控制相比，所设计的二阶滑模控制的暂态响应时间更短，动态性能更好。

图4 发电功率增加时双馈电机采用二阶滑模控制的仿真波形

图5 发电功率增加时双馈电机采用传统PI控制的仿真波形

图6～图7为两种不同控制方案下DFIG系统在风机功率突增时的仿真波形图。当风机的发电功率突减时，中间直流侧电压将会波动，并在0.025 ms后稳定(二阶滑模控制)。由于发电功率突减，电网电电流幅值也将减小。PI控制方案下当风机的发电功率突增时，中间直流侧电压也会波动，并在0.04 ms后稳定。由于发电功率突减，电网电电流幅值也将减小。因此，当风机发电功率变化时，与传统PI控制相比，所设计的二阶滑模控制的暂态响应时间更短，动态性能更好。

图6 发电功率减少时双馈电机采用二阶滑模控制的仿真波形

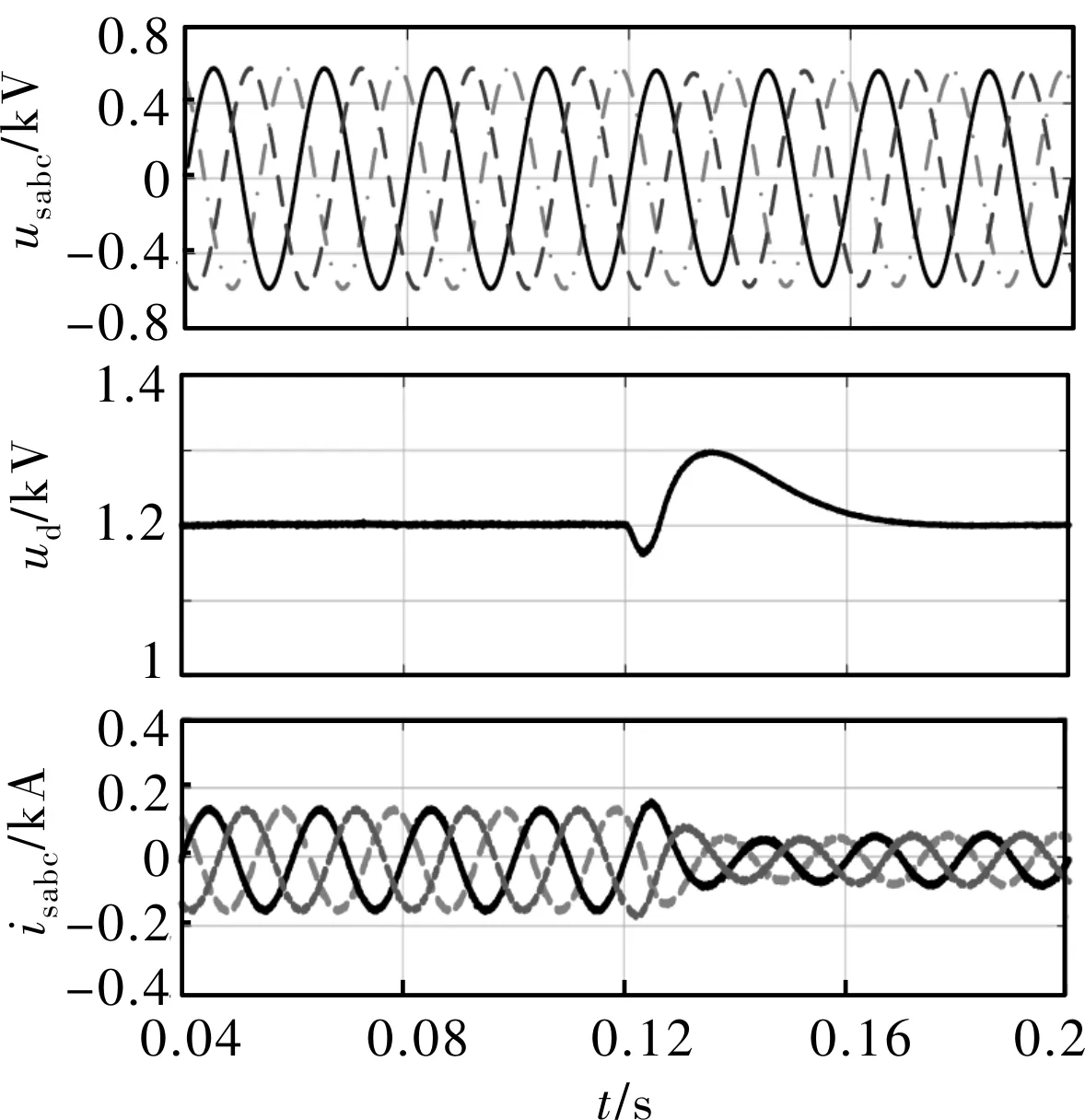
图7 发电功率减少时双馈电机采用传统PI控制的仿真波形

图8为所设计的二阶滑模控制方案下DFIG系统在直流电容值减少30%的仿真波形图。由图可知，当风机的发电功率突增时，中间直流侧电压将会波动，并在0.035 ms后稳定。由于发电功率突增，电网电电流幅值也将增大。图9为传统PI控制方案下DFIG系统在直流电容值减少30%的仿真波形图。由图可知，当风机的发电功率突增时，中间直流侧电压将会波动，并在0.05 ms后稳定。由于发电功率突增，电网电电流幅值也将增大。因此，当直流电容扰动时，与传统PI控制相比，所设计的二阶滑模控制的暂态响应时间更短，动态性能更好。

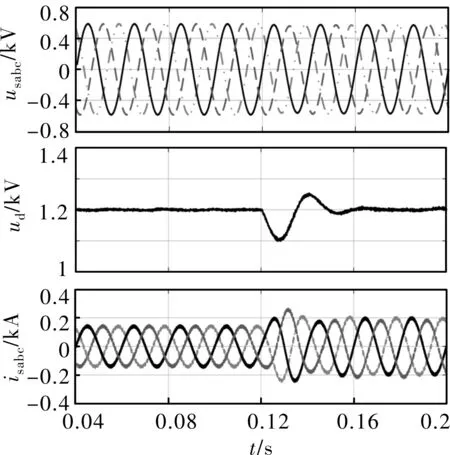
图8 直流电容减小时双馈电机采用二阶滑模控制的仿真波形

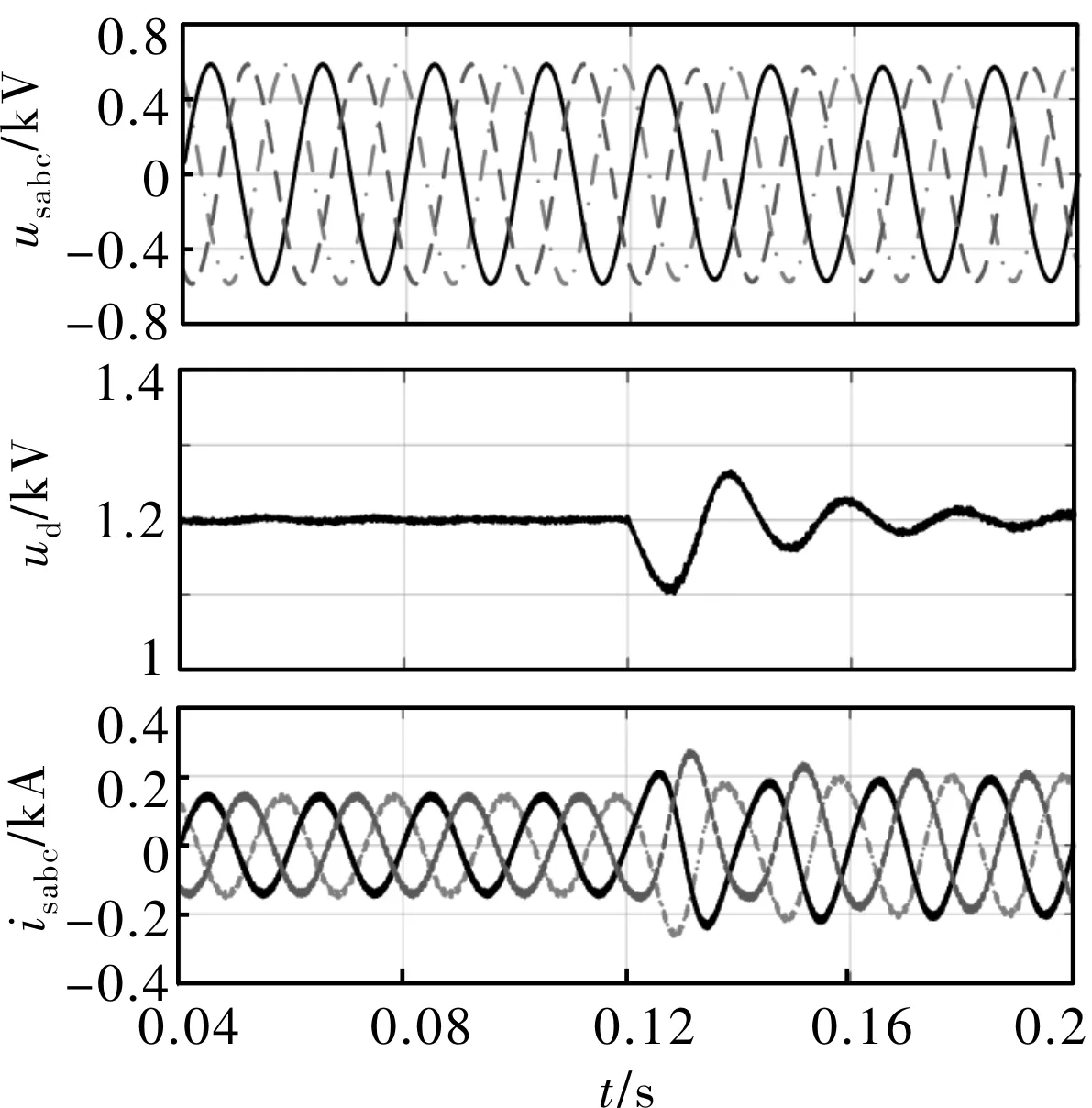
图9 直流电容减小时双馈电机采用传统PI控制的仿真波形

4 结 论

为了提升双馈感应发电机(DFIG)网侧变换器的动态性能，提出了一种二阶滑模非线性控制方案,可有效地提升DFIG的直流侧电压与网侧电流的动态响应。传统的DFIG的网侧变换器的通常采用双闭环控制方案，直流电压外环和网侧电流内环均采用比例积分控制方案。而在实际工况中，直流侧电容器电容可能会随环境改变而改变，并且DFIG系统的输出功率也和风速息息相关。因此，为了提升网侧变换器的鲁棒性，本研究针对DFIG的网侧变换器的直流电压环设计了一种二阶滑模非线性控制方案来替代传统的PI控制。最后，Matlab/Simulink仿真结果验证了所提的二阶滑模非线性控制在风机功率变化及直流侧电容扰动时的鲁棒性。