基于量子蜂群优化的神经网络工程造价预测

刘毅然,张福泉

(1.新南威尔士大学土木工程学院,悉尼 2052; 2.闽江学院计算机与控制工程学院,福州 350108)

工程造价预测作为大数据技术在工程成本预估中的一项重要应用,有效提高了工程项目资金使用的预见性和合理性。通过对各种工程类型的样本特征进行大数据分析,可以有效预见单位造价和总造价。[1]通过工程成本预测,一方面有效提高建设实施控制策略,降低资金浪费,另一方面为招投标提供合理佐证,提高报价科学性,增强竞标竞争力。工程造价预测对资金管理控制策略的制定提供了有力的技术支持,[2]但是上述应用必须是建立在高效精准的工程造价预测算法之上。工程造价影响指标要素多且异构性强,导致数据特征受到施工环境影响具有一定变化,要根据这些特征获得较高的造价预测精度并不简单。当前支持向量机和神经网络模型是工程造价预测中的两种主流方法。为了进一步增强这两种方法对不同工程领域造价预测的适用性,对当前这两种方法有较多的改进方案。

在最新的工程造价预测研究中,吴飚等人[3]采用贝叶斯网络建立造价预测模型,实现了公路造价的合理预测,但该方法纳入的预测指标特征并不多,导致预测准确度存在一定的提升空间;杨凯等人[4]采用反向传播神经网络(Back propagation neural networks,BPNN)建立电网工程造价预测模型,并采用遗传算法(Genetic algorithm,GA)对NN参数进行优化求解,提升了BPNN模型工程造价预测准确率,但是会导致预测效率出现下降。本文采用神经网络算法用于工程造价特征训练,并采用量子人工蜂群算法用于神经网络核心参数优化求解,可以有效提高工程造价预测准确率及稳定性。

1 神经网络模型原理

设包含m个特征属性的样本Xk=(x1,x2,…,xm),k=1,2,…,n,n为样本总数,一般条件下n≤m,Xk经过网络激励后输出为Yk=(y1,y2,…,ym),下面对神经网络(NN)的模型结构进行数学描述。

输入变量通过隐藏层得到[5]

其中W1ij、θ1j和p分别表示第一隐藏层的权重、偏置及节点总数。

S1j经过激励函数后得[6]

根据实际隐藏层数量,求解所有隐藏层,最后获得输出,本文的数学描述以2层隐藏层为例展开。

设节点t的输出为Lt,节点t至j的权重Vjt,第二隐藏层b2j输出为

其中p为第二隐藏层节点数。

Lt经过激励函数后得[7]

借助(9)和(10)式求解所有权重,从而确定神经网络结构模型。

2 量子蜂群优化的NN预测模型

在采用NN模型进行工程造价预测时,NN模型的核心网络参数可以采用公式(9)和(10)式来获得,考虑采用ABC智能算法对参数进行优化求解,下面将对ABC算法进行数学描述。

2.1 人工蜂群算法(ABC)

ABC算法的寻优过程实质是对最优适应度蜜源的探索过程,通过探测蜂进行规定运动边界的广度搜索,确定蜜源大致位置,然后采用跟随蜂进行细粒度搜索,获得最优蜜源。

初始化蜜源i,探测蜂的d维初始位置Xid是[9]

其中Ud为d维搜索边界上限,Ld为下限,d∈{1,2,…,D},D是总维度。

探测蜂从Xid处执行蜜源搜索动作,其在Ud和Ld范围内获得的新蜜源是Vid,其位置为

其中j≠i,φ∈[-1,1],Xjd≠Xid且属于[Ld,Ud]范围内。

当探测蜂获得新蜜源Vi(Vi=[Vi1,Vi2,…,Vid])后,调整适应度fi[10]

根据fi计算值,将Vi和Xi两者中较大的调整为新蜜源。

探测蜂将探测到的所有蜜源数据传递至跟随蜂挑选,跟随蜂选择其偏好蜜源概率pi为

其中SP为所有蜜源数量。

探测蜂搜索蜜源的策略为:当迭代次trial达到最大次数Itrmax时,则重新跳转至公式(11),否则继续找最优蜜源。

因此本文借助量子编码方式,防止出现ABC算法优化NN参数导致工程造价预测效率和准确度不高的问题。

2.2 量子优化

量子的比特表示为[11]

将上式用矩阵表示

2.3 基于QABC-NN的工程造价预测建模及流程

在采用QABC-NN模型进行工程造价预测之前,需要提取准确的工程造价预测指标变量,工程造价数据指标要素多,在做工程造价分析时,需要选择合适的分析对象,这样有助于更精准地对多个指标进行深度剖析,以细粒度地获取精确的工程造价数据,从而实现精准地造价预测。

首先,构建NN工程造价预测模型,然后运用QABC算法求解NN网络参数,得到稳定的QABCNN工程造价预测模型,最后输入合适的指标数据进行工程造价预测并获得预测结果。

3 实例仿真

为了验证QABC-NN模型在工程造价预测中的性能,进行实例仿真。仿真数据来源为某大型房产公司2015-2019年度的300栋建筑的工程造价数据,组成300个仿真样本,根据多篇参考文献,选择如表1的15个造价指标要素进行分析。首先验证QABC-NN模型的工程造价预测准确率及RMSE,其次验证QABC算法对NN在工程造价中的性能影响,最后将常用工程造价预测算法和本文预测算法相比,对比常用算法的预测性能。

表1 工程造价指标要素

3.1 QABC-NN的预测性能

采用QABC-NN模型对200个数据样本进行工程造价预测训练,获得稳定的QABC-NN预测模型,然后对剩余100个样本进行测试分析。

从图2可以看出,对于100个测试样本,通过QABC-NN模型预测的单方造价与实际造价值非常接近,只有少数样本其实际造价与预测造价有较大偏移。从图中看出,100个测试样本的单方造价围绕2000元/m2波动,其造价范围保持在[1000,2700]之间。为了更加清楚地反映100个测试样本的预测误差情况,统计单方造价绝对误差,具体见图3。

从图3得出,100个测试样本的单方造价绝对误差保持在[0,160]范围中,单方造价绝对误差为0的样本共计7个,绝对误差为160的有2个。

3.2 量子蜂群的优化性能

为了进一步验证量子蜂群算法对NN聚类的优化性能,分别采用NN、ABC-NN和QABC-NN模型对100个测试样本进行工程造价预测仿真,鉴于篇幅原因,表2展示了其中10个样本的预测结果。

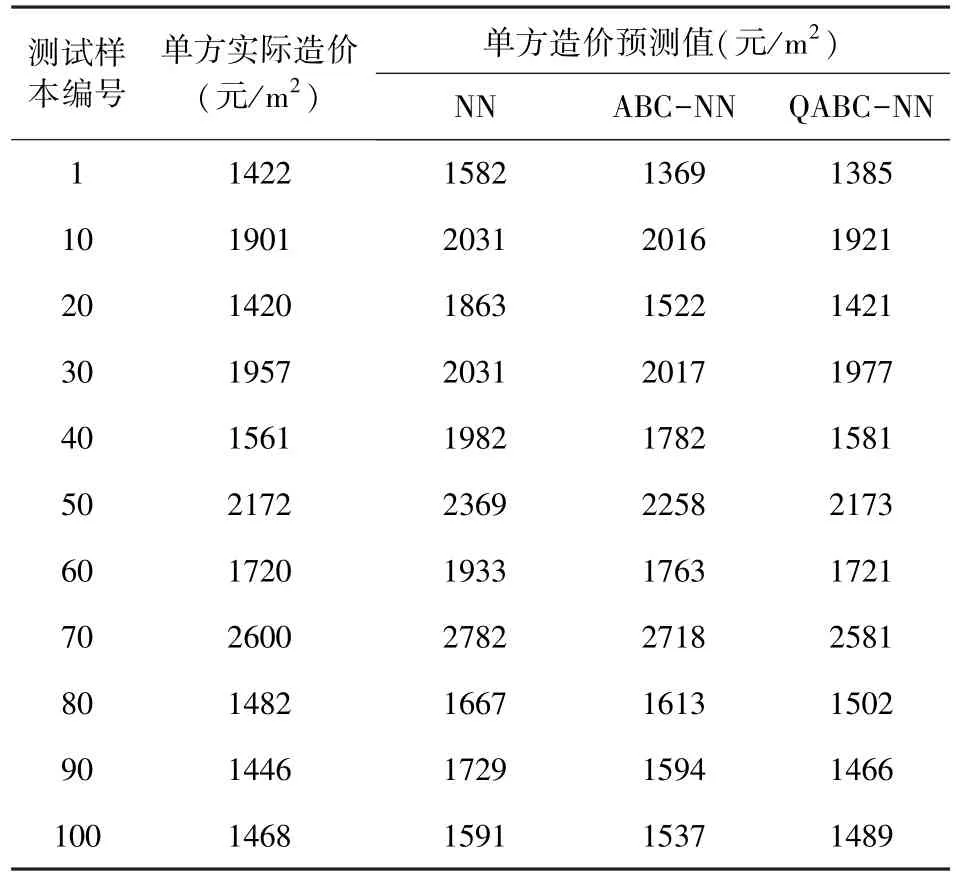
表2 3种算法的单方造价预测结果

表2列出的10个测试样本,QABC-NN模型的单方预测造价与单方实际造价最接近,ABC-NN模型次之,NN模型相差较大,其中样本编号为20、50和60时,QABC-NN模型的单方造价预测值与实际单方造价几乎一致,预测准确率非常高,NN模型的预测差值均在100元/m2以上,这说明经过QABC算法对NN的网络参数进行优化之后,有效提高了NN模型的工程造价预测准确率。

表3 3种算法的单方造价预测RMSE

从表2知,3种工程造价预测算法的稳定性差异并不大,基本保持在同一数量级,但是QABCNN模型仍表现了最优RMSE性能,ABC-NN次之,NN模型最差,在样本编号30时,QABC-NN表现出了最低RMSE值2.061e-2,而NN模型在样本编号为10时,获得了最差RMSE值4.309e-2。这说明相比于反向传播求解参数,QABC优化获得的NN网络参数更有效,QABC-NN预测算法更稳定。

3.3 不同预测算法的性能

为了进一步验证QABC-NN模型的预测性能,将近年来其他研究者在工程造价中采用的预测算法SVM[14]、BP神 经 网 络[15]、ABC-SVM[16]和QABC-NN进行预测精度对比。异较大,其中QABC-NN模型RMSE值最优,ABCSVM次之,SVM算法最差。从预测时间方面来看,ABC-SVM算法最差,大约需要55s才能获得稳定的RMSE值,而其他3种算法仅需要50s达到稳定。综合而言,QABC-NN模型的预测准确率和稳定性均高于其他3种算法,表现出了更优的工程造价预测性能。

4 结语

图4展示了4种算法的预测单方造价值与实际值的拟合程度,其中QABC-NN模型所预测的单方造价与实际造价拟合度最高,特别是在样本编号为[60,100]区间,ABC-SVM次之,SVM最差,这表明QABC-NN模型的单方造价预测准确率最高,传统的SVM和BPNN工程造价预测准确率并不高,经过ABC改进后的SVM和NN模型的工程造价预测准确度上升明显,这说明通过智能算法对SVM和BPNN的参数进行优化求解之后所获得的预测准确率性能远高于参数的传统求解方法所获得的预测准确率。

从图5得,4种造价预测算法的RMSE性能差

采用QABC-NN模型用于工程造价预测,通过NN模型对多个造价特征的深度训练,并借助QABC算法的NN网络参数寻优,能够获得较好的工程造价预测结果。通过对建筑工程造价样本的单方造价成本预测,QABC-NN模型的预测准确率远高于其他算法,且表现出较强的预测稳定性。后续研究将进一步改进ABC算法,提高QABC算法对网络参数寻优的效率,以进一步降低QABC-NN模型的工程造价预测时间,增强大规模工程造价预测的适用性。