基于Canny算子的图像边缘检测优化算法
姜玲燕,李 俊,王嘉琦
(1.苏州幼儿师范高等专科学校基础部,江苏 苏州 215000;2.飞依诺科技(苏州)有限公司,江苏 苏州 215000;3.南京师范大学外国语学院,江苏 南京 210097)
图像中均会产生图像边缘,图像边缘包含了物体形状、阴影、图像突变部分以及图像纹理等丰富的信息,图像边缘信息也是各类图形图像软件识别、理解以及处理图像的基础。目前,图像边缘提取已经广泛应用于图像分割、医学造影、数字图像压缩、光栅图像矢量化、图像识别等领域中,由于各行各业对于图像处理的要求以及评价标准不一致,没有一种边缘检测算法完全适用于所有情况。文献[2-3]详述了各种边缘检测的相关方法,常见的算子有Prewitt算子、Roberts算子、Laplacian算子、Sobel算子、Canny算子[1]等,此类算子是基于图像像素梯度进行边缘提取,基于遗传算法、松弛法、蚁群算法等提取的图像边缘效果较好,但是算法较为复杂,小波变换等则是以信号处理为基础的边缘提取技术。本文从边缘提取算法的空间和时间复杂度以及数据的有效性,利用数学形态法[4-6]对Canny算子进行改进。实验表明,本算法普遍适用于灰度图和RGB图像的边缘提取。
1 算法梗概
本文的图像边缘检测算法分为三个步骤,即边缘预处理、边缘提取以及边缘优化,具体如图1所示。
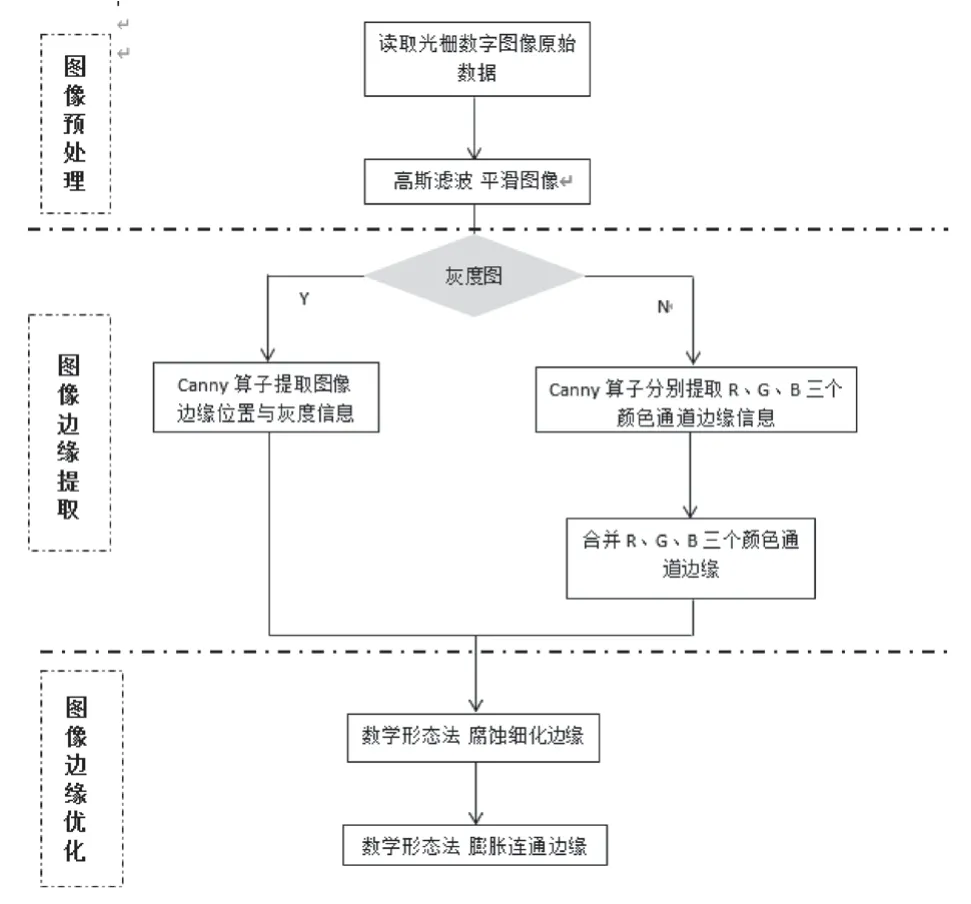
图1 算法流程图
(1)图像预处理:运用高斯函数对图像进行去噪,即去除图像在数字化过程中所产生的干扰信号,从而提高后期图像处理的精度;
(2)初步提取图像边缘:利用一阶偏导有限差分,计算图像全局梯度的幅值和方向,并对图像梯度进行非极大值抑制,最后根据设定的高低阈值检测和连接边缘;
(3)边缘颜色信息提取:根据步骤2,分别提取R、G、B三个颜色通道的边缘,然后合成为一个边缘。
经过上述步骤可以得到灰度图或RGB图像的边缘信息,根据已提取的图像边缘信息,可以分两步对边缘进行优化:
(1)利用数学形态法细化重叠的边缘,从而减少边缘数据量;
(2)利用数学形态法连接断裂的边缘,从而增强边缘连通性。
1.1 边缘信息提取
图像边缘是指图像像素灰度值或RGB图像中某一颜色分量呈现阶跃型或者屋脊状变化的像素集合,其主要分为屋顶状和阶梯状边缘[7],如图2所示。边缘检测的本质是分离图像中的目标与背景,从而突出图像的目标部分。
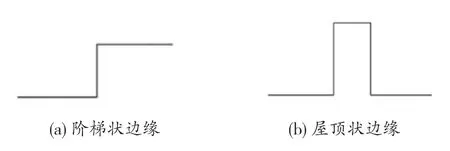
图2 图像边缘类型
Canny算子的主要步骤描述如下:
(1)对原始图像进行去噪
由于图像的边缘和噪声均属于高频分量,一些边缘检测算子往往很难分辨噪声和图像边缘,而误将噪声当成边缘信号。因此在对图像进行边缘检测之前,Canny算子先利用高斯函数对图像进行了去噪处理,从而确保边缘提取的准确性,图3是高斯分布,高斯函数如式1所示:
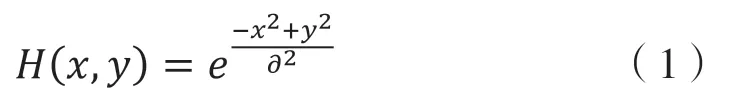
其中,图像的平滑度随着∂值的增大而增高,∂越大,滤波器频带越宽,图像越平滑,如图3所示。
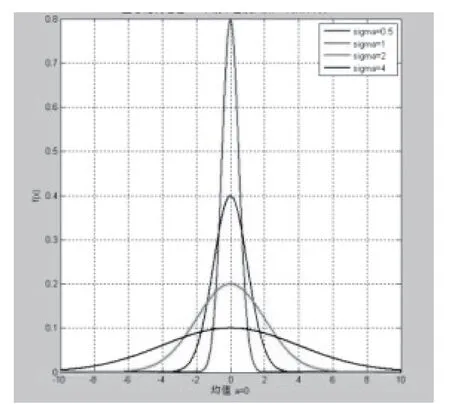
图3 高斯分布曲线
(2)计算图像像素梯度幅值和方向
图像边缘检测的本质是检测出灰度或颜色分量呈现突变的像素,并将这些像素点作为边缘点。边缘点像素梯度呈现屋顶状或阶梯性变化,因此计算图像全局梯度是Canny 算子中后续工作的依据。由于数字图像中边缘点X的梯度方向并不完全与其邻域方向相吻合,也由于实际数字图像中的像素点是二维矩阵,边缘点X的梯度方向两侧的点是一个亚像素点Y,因此就需要用一阶偏导的有限差分来得到最接近X点梯度方向两侧的像素值或Y点的梯度值。
(3)对图像梯度幅值进行非极大值抑制
部分检测环境下所说的非极大值抑制指的是检测中心点的值是否是某一个邻域内的最大值,而Canny算子中的非极大值抑制则是针对图像梯度而言,即寻找局部梯度幅值最大的像素点。根据John Canny在1986年的定义[1],若图像上某一点X满足以下两个条件则为需要增强的边缘点,否则为需要抑制的非边缘点:沿着X梯度法线方向的两个邻域的梯度值小于点X的梯度,且这两个邻域点的角度差不大于45°;点X的八邻域的梯度大小均小于某一特定值[8]。
(4)利用双阈值法检测和连接边缘
Canny算子通过设定一个高阈值H来提取有限的强边缘,将对比明显的背景与目标分开,设定一个低阈值L来控制边缘的连接,从而得到单像素的边缘。具体步骤如下:
将梯度值小于L的像素灰度设置为0,得到图像a;由于L值较小,因此图像a保留了大量的细节信息。将梯度值高于H的像素灰度值设置为1,得到图b;由于图像b的阈值较高,去除了大部分噪声的同时也损失了部分边缘信息,导致部分边缘的断裂或缺失。因此为了得到更加精准的边缘,以图b为基础,图a为补充连接边缘。这种做法能有效检测图像的强边缘而删除虚假边缘。不同的图像,高低阈值的选取也不一样,若L设置得过高则会丢失一些细小边缘; 若H设置得过低会漏检一些真实边缘。因此高低阈值的选取十分重要,应根据不同的图像以及所需边缘的精确度调整高低阈值。
1.2 边缘颜色信息提取
对灰度图进行边缘提取时只需要提取图像的边缘位置信息及灰度值,而RGB图像的边缘提取工作则需要提取边缘点的位置信息及RGB信息作为图像特征信息,这些特征信息的集合对于图像的采集、处理都具有重要的意义。
通常人们根据一定的彩色模型对RGB图像进行处理,彩色模型是指颜色空间的集合,而这个集合中的所有颜色都是通过某一个彩色模型计算所得,即根据若干个颜色分量计算得到颜色域中的所有颜色。由于红、绿、蓝三色是自然界中所有颜色的三基色,根据图像的RGB值,设定的RGB模型如公式2所示:
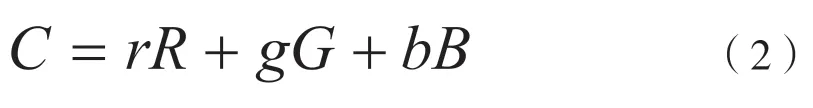
本文为了获取图像边缘的细节信息,利用Canny算子分别提取RGB图像中红、绿、蓝三种颜色的边缘,并将提取的三个边缘图层叠,得到最终的边缘图,如图4所示:左边三幅图分别为红、绿、蓝三种颜色的边缘,最右边为三张图片叠加在一起后的最终边缘。由R、G、B三基色的边缘所合成的边缘图,保留了RGB图像中各颜色分量的边缘细节信息。但合成的相邻边缘之间间隔过小,增加了边缘提取的数据冗余度,因此需要对边缘点进行后处理。
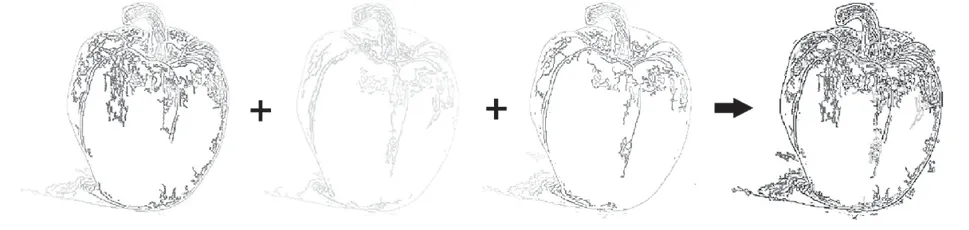
图4 R,G,B三个通道分别提取的边缘以及合成的边缘图
1.3 细化边缘和增强边缘连通性
为便于图像处理,需要降低图像边缘的数据冗余度,因此需要对原始图像边缘进行细化。
边缘细化主要是在保证图像边缘几何、拓扑结构不变的情况下,从原始边缘上寻找那些满足条件的边缘点,并标记为可删除,最后将这些满足条件的点从原始边缘上“剥离”,最终得到一个像素的细化边缘。但这些算法要求遍历次数多,容易过度“剥离”,因此并不适用于所有图像的边缘细化。
本文借鉴Serra提出的数学形态法[9],对提取的图像边缘进行细化处理。数学形态法以集合论为基础,应用在图像处理领域便是将一幅图像中的所有像素点称为一个集合,图像中的像素点及探针结构元素(本文一般为可移动的集合)则作为集合中的元素,利用设定好的探针在图像集合中的位移,进行各类集合运算,变换得到一个新的图像集合。同理,利用数学形态法优化图像边缘时,将Canny算子提取的边缘点阵作为一个集合,与预先设定的探针进行交、并、补等运算得到优化后的边缘。
数学形态法由组代数运算子组成,基础运算主要有腐蚀、膨胀运算(先腐蚀再膨胀),闭运算(先膨胀再腐蚀)等。集合X分别被探针S进行上述的操作可表示为式(3)至式(6):
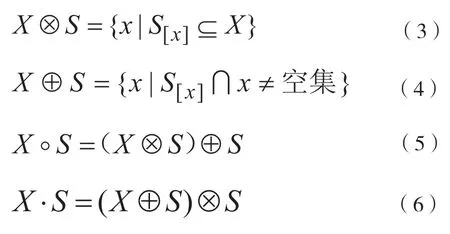
其中X为给定图像的像素点集,S为探针。腐蚀操作用于消除边缘中的冗余部分;扩张操作用于连接图像断裂的边缘,增强边缘连通性;开操作使提取的边缘更加平滑;闭操作在平滑边缘的同时还连接局部断裂的边缘。以上四种数学形态法的基本运算可通过推导组合成各种不同的图像处理算法。数学形态法可利用腐蚀操作细化图像边缘,也可针对不同的情况设定不同的探针增强图像边缘连通性等。
本文设计的探针如图5所示,设定的膨胀探针(图5a)和侵蚀探针(图5b),其中A代表图像边缘点,膨胀探针每旋转45°便得到一个新的膨胀探针,旋转360°以后得到了7个不同的膨胀探针。利用数学形态法优化边缘信息的算法概括如下:先用膨胀探针对Canny算子提取的边缘进行膨胀,得到连通性更好但冗余度较高的边缘(称为O),再利用侵蚀探针对O进行腐蚀得到数据量较小的边缘。
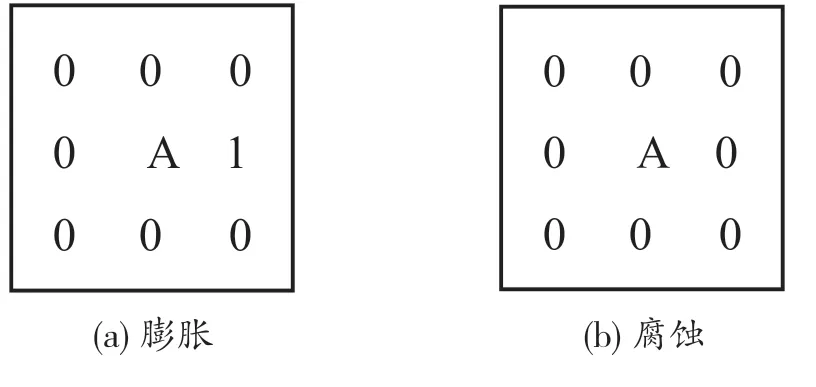
图5 膨胀和侵蚀的探针
2 结果与分析
本文采用VC++6.0和OpenGL在PC机上实现了边缘提取的优化算法,实验结果表明,本算法普遍适用于RGB图和灰度图的边缘提取,并且提取的边缘相对封闭,数据量较原始边缘数据量小。将高斯模糊、高阈值、低阈值三个参数分别设置为0.4、0.9、0.4,且遍历原始边缘图一次所得到边缘提取效果如图6所示。图7为蛋黄边缘提取的局部放大图,可见,优化后的算法所提取的数据量明显减小(具体数据如表1所示)。同时,根据改进前后的边缘分别对图像进行重建(如图8所示):根据原始Canny算子提取边缘的重建图有部分颜色溢出,而优化后的边缘更利于图像重建,其连通性更强。
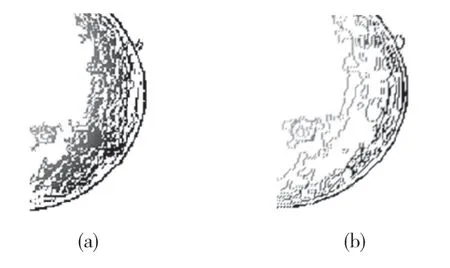
图7 蛋黄边缘局部放大图:Canny算子提取边缘(a),优化后边缘(b)

图8 边缘改进前后重建的光栅化图像比较
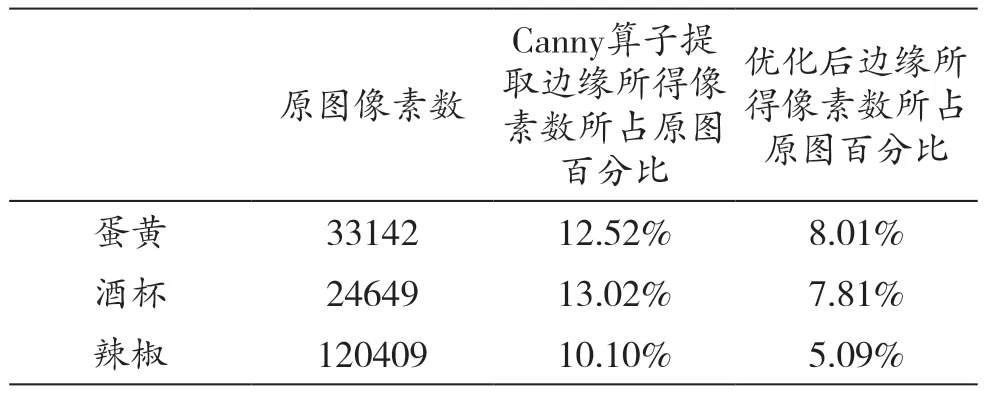
表1 图6中各项数据统计
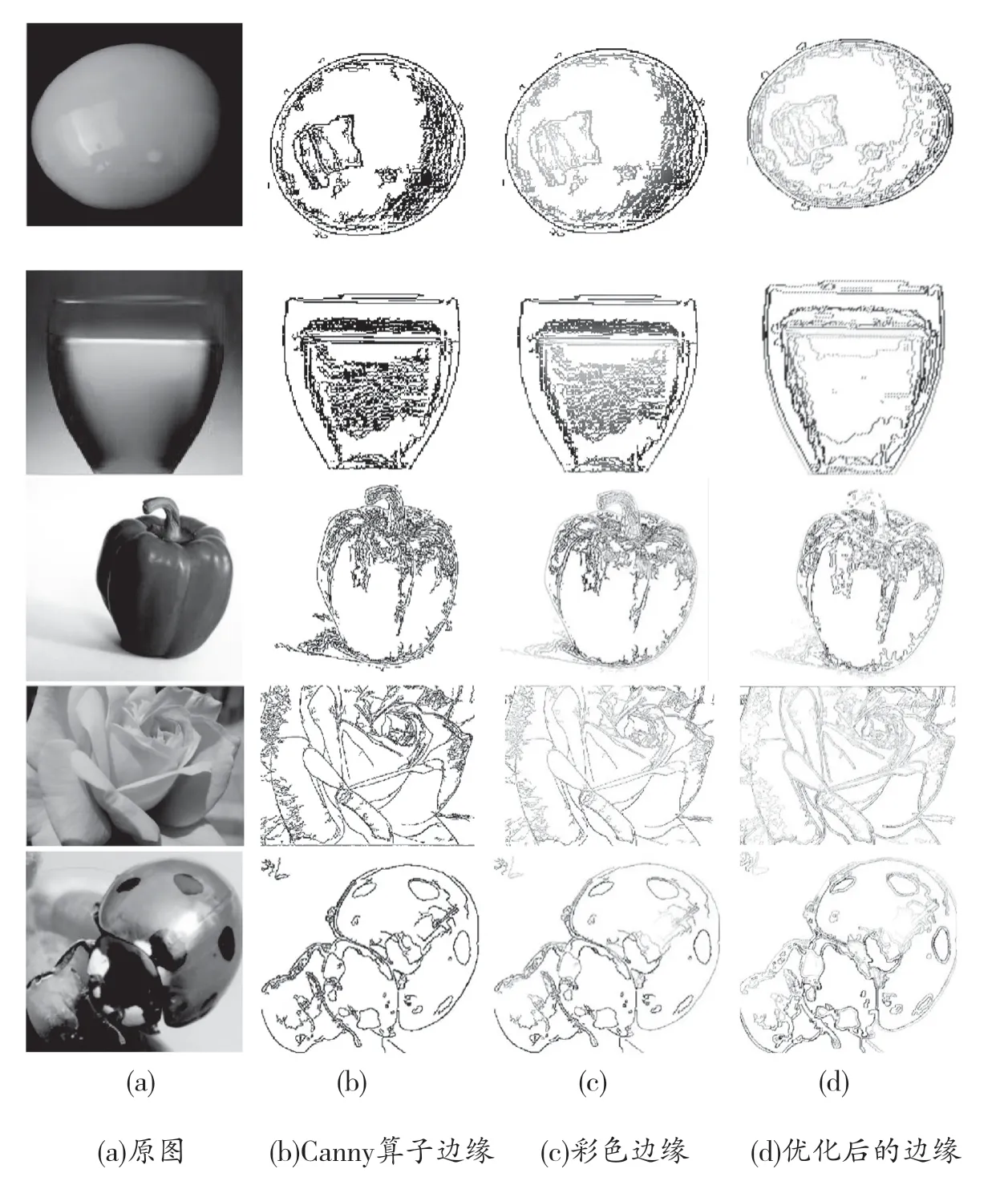
图6 图像边缘提取实例
3 结语
本文提出一种利用数学形态法中的四种基本运算进行推导组合优化Canny算子提取图像边缘信息的算法,并对算法进行了验证。今后考虑在此算法基础上,继续进行数据量和算法效率的优化,并将其运用于图像识别、图像压缩、图像矢量化[9]等各类图像处理领域。

