数学课程内容下的数学建模教育

姜咏梅王志俊

（1.江苏建筑职业技术学院公共基础学院，江苏 徐州 221116；2.中国矿业大学数学学院，江苏 徐州 221116）

0 引言

众所周知，数学建模是对现实问题进行数学抽象，用数学语言表达问题，进而用数学方法构建模型并解决问题的过程。数学建模是发展现代应用数学的重要突破口，它搭建了一个数学与外部世界紧密联系的桥梁，是数学走向应用的必经之路。

对于大学生来说，各个领域的许多实际问题即使在了解了相关背景的情况下也很难借助于所学高等数学知识加以解决。究其原因，在高等数学教学过程中，教学内容理论推导和计算居多，应用性（特别是开放应用性）的教学内容偏少，数学教学内容和专业知识之间的衔接存在一定的问题。

对于此问题，叶其孝在将数学建模思想和方法融入高等数学课的教学方面做了深入的讨论并提出了值得借鉴的建议。受此启发，本文结合在国内具有一定影响力的五一数学建模竞赛中一些典型题目，探讨数学建模教育在数学课程内容方面的有机融合。

五一数学建模竞赛是由中国矿业大学、江苏省工业与应用数学学会和徐州市工业与应用数学学会联合主办的在国内具有一定影响力的数学建模赛事。该项赛事规模不断扩大，2021年第十八届五一数学建模竞赛共吸引了近6 000支队伍、17 000多名学生参赛；赛事质量也不断提高，往届赛题中许多问题的解决为相关单位带来了良好的经济和社会效益。五一数学建模竞赛于每年的“五一”期间（连续72小时）以参赛队为单位进行比赛，参赛队从三道竞赛题目中选择一题进行解答并提交参赛作品。

1 课程内容及相关数学模型

在多数高等院校中，高等数学课程群主要包括高等数学、线性代数和概率论与数理统计三大课程。通过对这三大课程结构数学建模专题的内容要求和学业要求进行分析比对，结合五一数学建模竞赛历年来的赛题，选取了以下几种常见的数学建模类型：基于指数函数的经济数学和社会数学模型；基于线性方程组的线性规划模型；基于统计学的聚类分析方法和线性回归模型，以及相应的题目素材作为课程内容供参考使用。

1.1 基于指数函数的经济数学和社会数学模型

指数函数是高等数学中所要研究的一类基本函数，是一种描述客观世界变量之间指数增长或衰减关系和规律的数学工具，与指数函数相关的模型在许多领域有实际背景和具体应用。经济数学模型和社会数学模型是数学建模专题所要研究的内容之一，而像存款贷款规模控制、经济增长预测和人口增长预测等一些经济社会实际问题均可通过指数函数模型来提供理论依据或解决方案。同时，在理解指数函数的概念以及其中所蕴含的运算规律的基础上，学习基于指数函数的经济数学和社会数学模型将有助于理解指数函数的实际意义，感受指数函数在刻画增长率问题中的作用。

五一数学建模竞赛2018年B题“商业银行人民币贷款规模分配及盈利问题”、2016年C题“二孩政策问题”、2015年C题“生态文明建设评价问题”和2014年“延迟退休问题”等分别由经济和社会领域的实际问题加工而成。这些题目中的部分问题均可在简单了解相关背景知识的基础上，建立指数函数模型，进而寻得合理的解决方案。以2015年C题“生态文明建设评价问题”第四问为例，该题是基于某省生态文明建设改进措施效果的研究。对于如单位地区生产总值能耗、单位地区生产总值废水排放量、绿化覆盖率、人均公共图书藏书量等指标，可以采用指数函数模型来研究其未来的变化趋势。

1.2 基于线性方程组的线性规划模型

作为线性代数的主要研究对象之一，线性方程组是一类简单且重要的代数方程组。借助于矩阵和行列式，线性方程组的理论解法（如高斯消元法、克拉默法则等）已非常成熟；在计算数学中，其数值解法也日益完善。线性方程组有着广泛的应用，科学技术中的许多问题均可归结为解线性方程组。作为运筹学的一个重要分支，线性规划研究线性约束条件下线性目标函数的极值问题。通俗来说，在实际问题（如生产安排、货物运输等）中，线性规划是要找到一种最优的“方案”，使用或分配有限的资源（如原材料、车辆等）使得费用最省或者利润最大，以达到预定的目标。

五一数学建模竞赛2019年B题“木板最优切割方案”、2018年A题“徐州潘安湖风景区游览路线设计”、2017年A题“公交车排班问题”和2013年C题“整车物流调动系统”等均以数学中的优化理论为基础，根据题目要求建立目标函数，进而借助于计算机给出在特定约束条件下的最优解。而上述四道题目中对部分问题所建立的目标函数均是线性目标函数，均可以用线性规划模型得到解决方案。

1.3 基于统计学的聚类分析方法和线性回归模型

统计的教学活动应通过典型案例进行。应用统计是在概率与统计专题的基础上展开的，而聚类分析和线性回归模型是应用统计中的两个主要内容。聚类分析是一种对数据集进行分析和处理，从中寻找相似元素，以达到分类目的的方法。对数据集进行分类的目的不同，聚类分析的方法也各异。在此过程中，笔者将结合具体实例介绍K-均值聚类和分层聚类这两种易于接受的聚类方法。线性回归是一种用来确定两个或两个以上变量间互相依赖的线性关系的一种统计分析方法。在许多领域，特别是在经济学中，线性回归常用来作为一种实证工具来预测各种指标。将介绍一元线性回归和简单的二元线性回归模型以及利用最小二乘法原理对模型中的参数进行估计。

五一数学建模竞赛2019年C题“科创板拟上市企业估值”、2018年B题“商业银行人民币贷款规模分配及盈利问题”和2008年“股指期货套利问题”等题目都有来自不同领域的真实数据，都不同程度地涉及应用统计中的数据分析处理，进而确定不同要素之间的依赖关系或预测某一指标的走势。以2019年C题《科创板拟上市企业估值》为例，通过对中国A股市场和美国NASDAQ市场相关数据进行聚类，然后利用多元线性回归模型就可以定量分析估值水平与基本面指标、流动性指标之间的关系，进而给出差异性分析。这些方法和模型所得的相关结果对于研究我国科创板企业上市后的估值水平，都具有很好的参考价值。

2 数学模型应用与实践

以2019年B题基于线性方程组的线性规划模型“木板最优切割方案”为例。本题在切割大块木板的过程中，需要设计合理的切割方案，从而降低生产成本，减少材料浪费，提高材料利用率，使家具厂经济生产效益最大化。问题1～5均可归结为线性规划问题。比如在问题1中，为了使木板的利用率最大，只需产品P1的总面积最大，即一块木板能切割产品P1的数量最多，可分别按长度和宽度进行优化组合，取两者利用率更大者作为最终方案。以按木板长度优化组合为例，可以建立如下的数学模型：

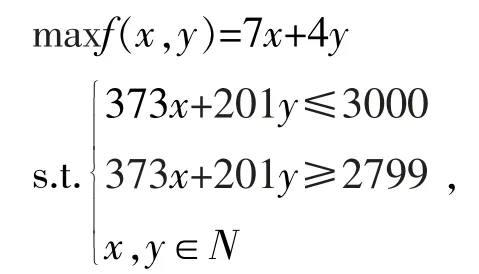
式中，x表示产品P1横向排列的数目，y表示纵向排列的数目。显然，该模型的目标函数f（x，y）为线性函数，约束条件为线性不等式，它是线性规划模型。（注：x，y取自然数表明它还是一个整数规划模型。）

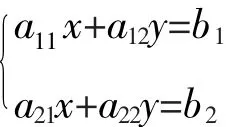
注意到，当线性方程ax+ay=b变成线性不等式ax+ay≤b时，它在二维平面上就由一条直线变成该直线一侧的半平面了。如上述模型中的线性不等式373x+201y≤3 000就表示直线373x+201y=3 000左侧的半平面，373x+201y≥2 799就表示直线373x+201y=2799右侧的半平面。因此，模型中的前两个约束条件表示的是两条平行直线中间的区域（如图1所示）。

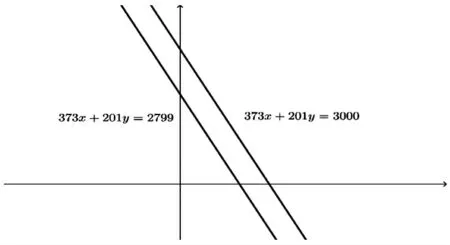
图1

模型是要求和使得目标函数取得最大值，从直观上看，越靠近直线的点取得的函数值越大。在不考虑是否为自然数的情况下，取得最大值的位于右侧的直线上；当考虑和均为自然数时，取得最大值的应在中间区域且接近右侧直线。而满足这一条件的点只有。通过简单的代入计算即得：目标函数取得最大值的整数解为且取得最大值59。该问题详细讨论了线性规划模型与线性方程组之间的关系。

3 结语

结合数学课程内容开展数学建模教育的目的是希望学生能够在学习数学知识的基础上领略数学建模的思想和方法，提高学生学习数学的兴趣和应用数学的意识和能力，进而体会到数学在现实生活中的应用。在这一过程中，恰当的数学建模素材和数学知识之间的有机融合往往能够在教学上起到事半功倍的效果。从数学建模竞赛赛题的建模方法中挖掘素材、凝练数学原理，进而在数学教学中有针对性地进行剖解分析；从数学建模竞赛赛题的模型求解中发现方法、再现科学计算，进而在数学教学中有针对性地强化训练。这样就达到了将数学建模思想渗透到整个数学学习中的目的，从而提高学生的综合素质，为学生的可持续发展奠定基础。