未知周期性DoS攻击下基于事件触发的离散系统H∞滤波器设计*

丁 翔 胡松林 丁 飞

（1.南京邮电大学自动化学院、人工智能学院 南京 210023）（2.南京邮电大学先进技术研究院 南京 210023）（3.南京工程学院自动化学院 南京 211167）

1 引言

近年来网络化系统的研究对象日益复杂，同时对控制精度、稳定性，抗扰动性和自适应等控制性能的要求也越来越高。在网络化系统控制中，传感器、执行器和控制器等部件在系统层面上分布，并通过通信网络进行数据交换，增加控制系统灵活性、减少工程布线和降低成本维护［1］。在系统正常运行时，短期内传输的数据量会大幅激增，网络系统内数据包在传输中，将面临传统网络系统中延迟、丢包、采样频率过快的问题［2］。在网络控制系统中引入事件触发的通信方案（ETCS）就可以有效规避这类问题［7］，为网络数据传输减轻负荷，因此在各类网络系统中基于事件触发的滤波或控制问题逐渐成为许多学者研究的重点［4］。

离散化系统不仅可以有效降低时间复杂度，更能够进一步减小数据传输过程中负担。提高离散化物理系统的聚类和抗噪声能力，但是在提高系统抗噪能力的同时并不能保证其数据传输的稳定性，在这种情况下，使用H∞滤波方法研究状态估计问题，其可以保证噪声衰减水平［3～4］。因此H∞滤波问题已经被广泛应用在离散化物理系统中。

网络化控制的弊端在于它大大增加了控制系统受到网络攻击的可能性，进而产生网络攻击问题，由于拒绝服务（DoS）攻击方式简单、易达目的、难以防范和追查等特性［5～6］。DoS攻击已经成为一种常见的攻击方式［8］，因此许多工作者研究了离散系统在DoS攻击下的安全性问题。尽管许多文章中也都考虑到对离散系统的事件触发H∞滤波问题，亦或考虑在DoS攻击下的离散系统H∞滤波问题［10］。但是并没有将事件触发与DoS攻击同时考虑在内，设计一种更加有效的弹性H∞滤波器［13～14］。鉴于以上研究现状，本文将未知周期DoS攻击与事件触发机制进行融合设计协同H∞滤波器［15］。在对攻击建模过程中使用了离散系统的Lyapunov-Krasovskii函数方法和切换系统方法，最终实现未知周期DoS攻击下基于事件触发的离散系统的H∞滤波器协同设计［16］。

2 模型描述

2.1 系统物理模型

图1描述了在未知性周期的DoS攻击下基于事件触发的线性离散系统的弹性H∞滤波问题，其中物理系统模型用离散系统表示为

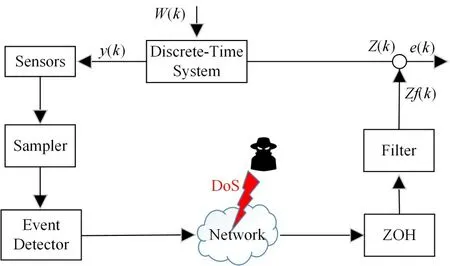
图1 DoS攻击下的滤波系统结构图

其中x(k)∈ℝn是系统的状态向量，ω(k)∈ℝν是系统外部噪声扰动向量且能量有界，y(k)∈ℝm为系统测量输出，Z(k)∈ℝp为系统状态估计信号。而矩阵A、B、C、D、L为系统常数矩阵。

设计如下形式的全阶滤波器模型：

其中xf(k)是滤波器的状态向量，Zf(k)是Z(k)的状态估计，是滤波器的输入，Af、Bf、Cf、Df为待求滤波器的参数矩阵。

2.2 未知周期DoS干扰攻击模型

拒绝服务攻击是一种恶意信号攻击，其出现将导致传感器到滤波器中的数据传输被迫中断。假设其干扰信号能量有限，干扰攻击模型设计如下形式：

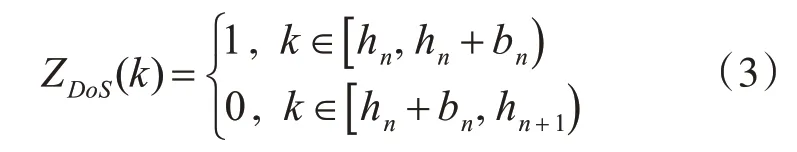
其中hn表示上一次攻击结束，开始正常通信时刻。bn表示本次正常通信时刻结束且下一次攻击开始时刻，hn+1表示下一次正常通信开始时刻。Ln={hn+bn}∪[hn+bn，hn+1)表示第n个拒绝服务攻击干扰信号间隔。那么hn+bn∈ℝ≥0表示第n个拒绝服务攻击干扰信号间隔的开始时刻，(hn+1-hn+bn)∈ℝ≥0表示第n个拒绝服务干扰攻击信号的区间长度。

假设在没有DoS攻击下，将离散系统测量输出y(ki，n)传输到滤波器输入y^(k)，反之滤波器输入为0，所以设计如下滤波器输入信号模型：

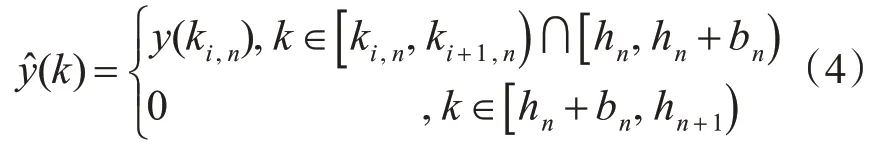
其中{ki，n}表示后续所设计事件触发机制所生成成功传送时刻，的集合，其中n∈N并且l(n)=sup{i∈N|ti，n≤hn+bn-1}。

2.3 弹性事件触发通信方案

为了节约离散网络系统的通信资源，我们引入一种弹性事件触发机制，用该机制来判断系统此刻采样状态，从而保证离散滤波误差系统的稳定性。

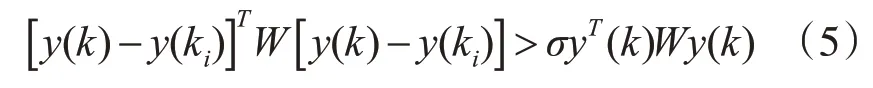
其中σ∈(0，1)是触发参数，k∈Z+，ki∈Z+事件发生器当前系统输出用y(k)来表示，W为触发参数矩阵。在未知周期的DoS干扰攻击信号的情况下，事件触发瞬间用如下表示：

其中n∈N，kij∈N，j∈N，i表示第n个干扰信号活跃周期内发生的触发次数。

当k∈D1，n∩I1，n，系统为稳定状态；当k∈I2，n时，子系统开环运行。离散滤波误差系统的稳定性取决于事件触发时刻，滤波器参数增益矩阵以及攻击频率和攻击时间。

2.4 滤波误差系统模型

在建立事件触发机制的切换系统后，为方便起见，设计如下时间间隔：ki，n+m)，其 中i∈Ω(n)，n∈N并 且ηi，n=sup{m∈N|ki，n+m≤ki+1，n}。令Wm i，n=[ki，n+m-1，ki，n+m)m，且I1，n=I1，n}。令

现定义两个如下分段函数：

其中0≤τi，n(k)≤τM，因此基于事件触发的采样状态表述为

基于以上定义全阶滤波误差方程为

当系统误差矢量满足：

时，系统切换方程表示为

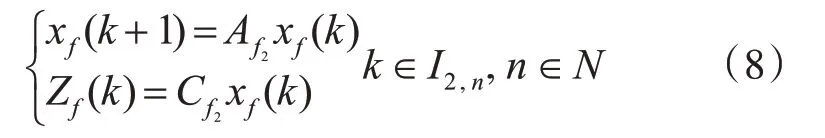
基于以上滤波器误差模型设计，我们要求所设计的误差系统程全局指数稳定且H∞扰动抑制量为γ，需要满足以下定义。

1）当系统在拒绝服务干扰攻击下，滤波器误差系统的外部扰动量ω(k)=0时，对所有变量u＞0，α＞0，γ＞0时 都 存 在不等式成立。其中为初始条件，ω(k)∈[ 0 ，∞)为连续函数。

2）当系统在拒绝服务干扰攻击下滤波器误差系统扰动量ω(k)∈[ 0 ，∞)时，在零初始条件下系统指数稳定，则给定扰动抑制量γ^，且离散滤波误差满足

3 主要结果

3.1 H∞性能分析

引理1：考虑对未知周期性DoS攻击且存在扰动ω(k)时离散滤波器误差系统问题，考虑系统（9）给定正标量λi，ui，τD，τb。如果存在适当维数的正定矩阵和 矩 阵W∈ℝ1×1，E1i，，使得如下线性矩阵不等式成立，则滤波误差系统指数稳定：

可以得到当k∈D1，n∩I1，n，n∈N，误差系统轨迹V1(k+1)≤λ1V1(k)。

当k∈I2，n，n∈N，误 差 系 统 轨 迹V2(k+1)≤λ2V2(k)。

证明：首先对滤波误差系统（9）选择分段的离散Lyapunov-Krasovskii函数i∈{1，2。}

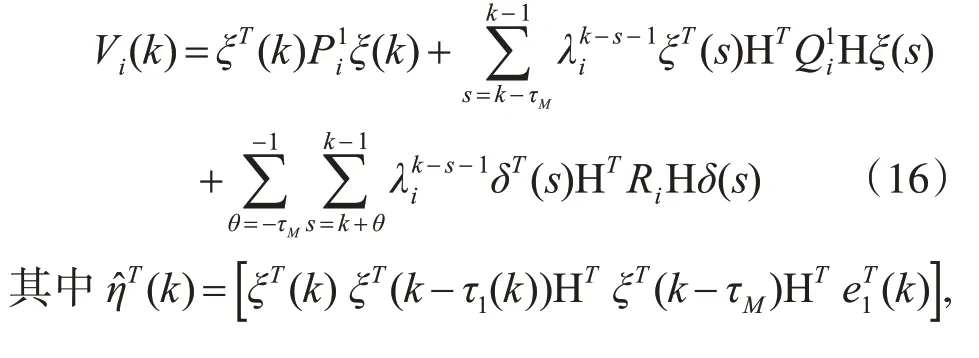
那么我们可以得到如下不等式：

情 况II：当k∈I2，n，n∈N时i=2，我 们 有ΔV2(k)=V2(k+1)-λ2V2(k)按照式（16）通过一样的处理，可以得到V2(k+1)≤λ2V2(k)证明完成。

情况III：对上述两种分段构造的离散Lyapunov-Krasovskii函数进行整理可得

根据式（14）～（15）进行代入化简，得到

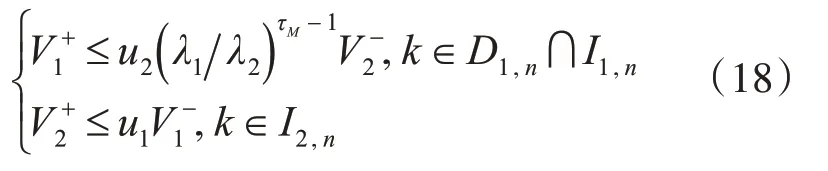
根据拒绝服务干扰攻击信号频率和持续攻击时间，当k∈I1，2时：

当k∈I2，2时：

结合离散系统平均驻留时间模型可以得到

当k∈I1，n时：

当k∈I2，n时：

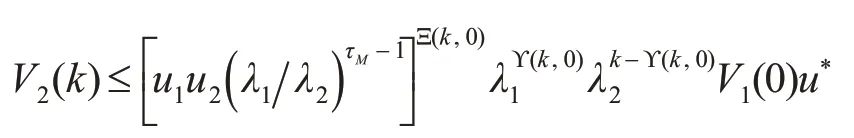
化简得

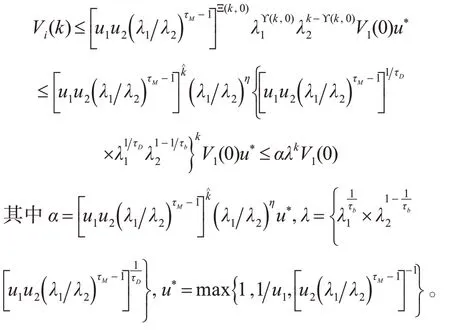
根据λ∈(0，1)且进行指对数运算得到

扰动下系统稳定分析证明完成。

3.2 H∞滤波器设计

定理1：在未知周期性拒绝服务攻击下，考虑存在系统扰动量ω(k)的离散滤波器误差系统问题，给定正标量λi，ui，τD，τb，若存在适当维数的正定矩阵和 矩 阵W∈ℝ1×1，Ei1，，使得如下线性矩阵不等式成立，则含扰动误差系统稳定：

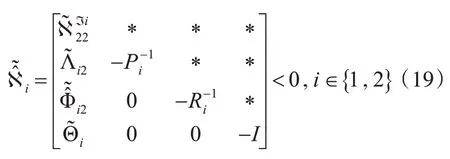
如果上述不等式存在可行解。那么所设计离散弹性滤波器参数为

证明：定义变量分别对有扰动下大矩阵（11—15）左乘右乘U31和，并定义新变量

4 数值仿真

接下来将用一个实例去验证本文设计离散滤波器的有效性，根据参考文献［8］数值，可以得到线性离散系统的具体参数为在考虑未知周期拒绝服务攻击下，使用攻击信号ZDoS(k)并且结合事件触发机制，求出所设计的离散滤波器参数增益矩阵Afi，Bfi，Cfi使得原系统全局指数稳定。令λ1=7，λ2=0.9，τD=0.5，u1=u2=1.05，τb=1.1，考虑离散系统采样周期为h=1，τM=0.009且σ=4，得到最佳扰动抑制值γ=4与触发参数矩阵W。

滤波器状态估计误差和系统与滤波器估计信号分别如图2、图3所示。从图中可以看到：1）在未知周期的攻击下离散滤波逐渐收敛并保持稳定；2）本文所设计的事件触发可以缓解数据通信负荷，并过滤外界干扰与攻击的影响。

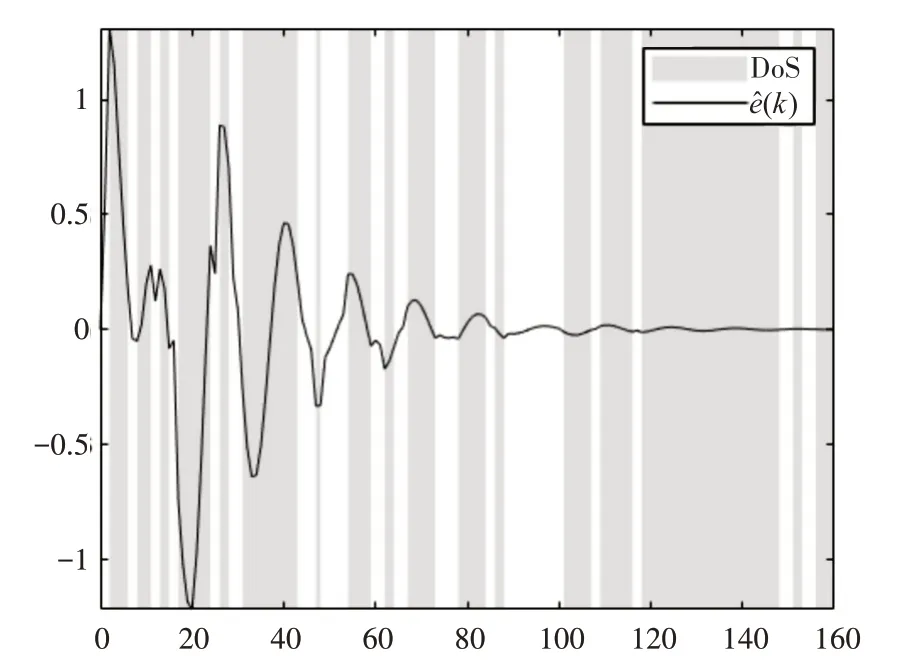
图2 状态反馈误差e^(k)

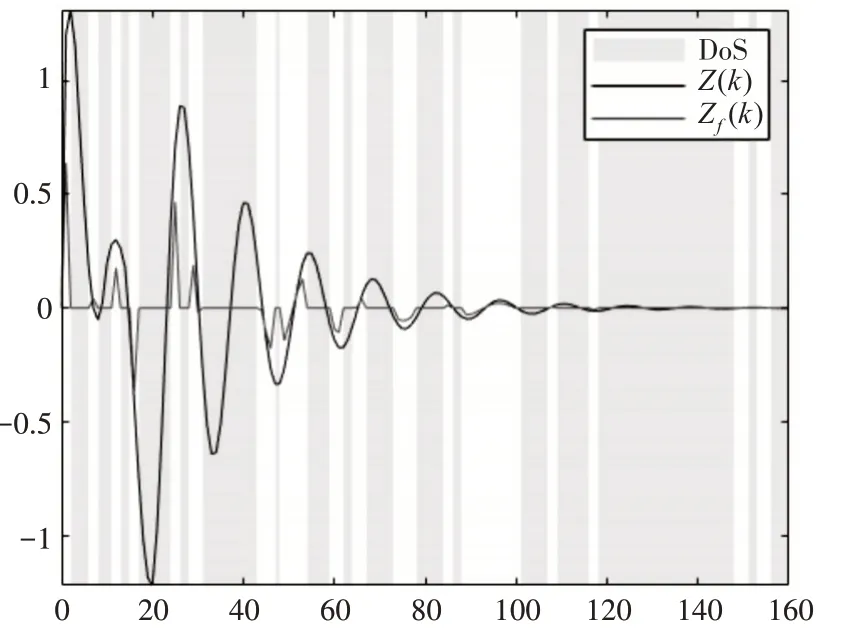
图3 待估计信号Z(k)和Zf(k)

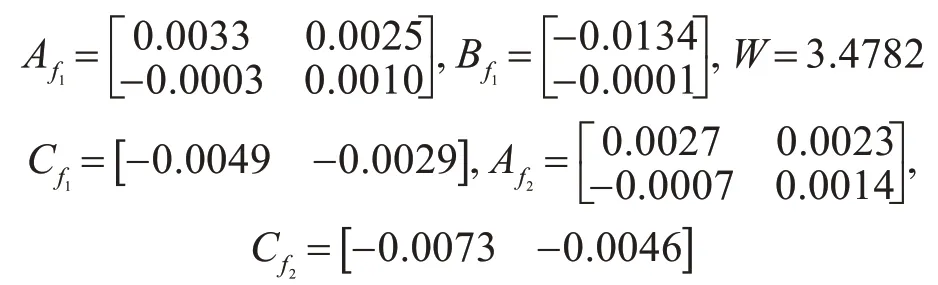
5 结语

本文主要解决离散系统通信传输过程中受到未知周期攻击下的H∞滤波器设计问题。将未知周期的DoS攻击与事件触发机制紧密联系在一起，综合设计出在拒绝服务攻击下新的事件触发通信机制。利用李雅普诺夫泛函推导出有效条件，并且使得滤波误差系统全局指数稳定与H∞扰动抑制最小。