基于最小轨道交叉距离的小行星顺访探测目标预筛选方法

张佳文 郑建华 李明涛

(中国科学院国家空间科学中心 北京 100190)

(中国科学院大学 北京 100049)

0 引言

一些深空探测任务为提高有效性，在完成主任务的转移途中边飞行边探测，进行小天体多目标探测。例如，伽利略号（Galileo）卫星从地球转移至木星途中顺访了小行星951 Gaspra 和243 Ida；嫦娥二号卫星在成功完成日地L2 点飞行探测后，对小行星4179 Toutatis 实现了飞越探测[1]。这类深空探测任务的轨道设计中，在主任务标称轨道附近，一般通过轨道递推求解探测器与小行星的相对距离来确定潜在探测目标[2-4]。

文献[2]在伽利略号卫星轨道设计中，将小天体飞越探测目标搜索策略分为三步。第一步，针对4000 颗左右的小天体，分别计算其与探测器之间的相对距离，保留相对距离小于1.5×107km 的候选目标星。第二步，遍历地球发射时间与木星到达时间，计算探测器与上一步筛选出的小天体之间距离最近时的时间与相对距离，选出可实现零距离或近零距离飞越的待选目标以及相应的地球发射时间和木星到达时间组合。第三步，针对待选目标星，将飞越小天体时间、距离、方位作为优化变量，对轨道进行重新优化设计。

文献[3]对嫦娥二号卫星探测小行星目标的选择主要分为三步。第一步，在小行星轨道特征和高精度轨道递推模型基础上，结合卫星寿命约束，选取近地小行星进行轨道递推，搜索满足2012 年10 月至2013 年6 月与地球最近距离小于1.5×107km 的目标。第二步，根据嫦娥二号卫星成像约束与潜在目标星的物理特征，确定小行星飞越探测的潜在备选目标。第三步，根据日–地–月系统转移轨道两点边值问题的求解，通过分析潜在备选目标飞越探测的机会与速度增量，得到嫦娥二号卫星再拓展任务飞越探测目标小行星为4179 Toutatis。

文献[4] 在得到2020—2025 年间向木星飞行燃料最省方案中较好的引力辅助序列为金星—地球—地球后，结合多任务探测，研究探测器在飞向木星途中穿越小行星主带飞越探测小行星的轨道设计中，将探测器飞越小行星活动区域轨道段平均划分，对276002 颗小行星计算在每一时间节点的位置，与探测器位置进行比对，统计二者相对距离小于可接近标准3×106km 的目标作为候选目标星，再从搜索结果中选择飞越目标，重新设计轨道。

实际工作中，当探测器飞行轨迹范围内的小行星数目庞大，并且标称轨道弧段长时，直接通过轨道递推的方式筛选目标计算量非常大。针对此问题，文献[5] 在嫦娥二号探测小行星任务转移轨道设计中，根据已编目小行星的轨道分布，首先基于近日距和远日距筛选出地球轨道附近的小行星，作为进一步精确计算小行星目标的前提，再基于飞行任务约束选择合适交会目标。这种预筛选方法对于地球附近的探测任务顺访小行星目标选择效率的提升有效果，但对于飞往外太阳系的探测任务不适用。

因此，针对直接通过轨道递推的方式来筛选目标计算量非常大的问题，本文提出在轨道递推计算二者相对距离之前，基于小行星轨道的形状和空间位置计算二者轨道在空间中的几何最近距离，预筛选出满足飞越探测距离约束的探测目标思路。研究中两轨道在空间中几何最近距离即最小轨道交叉距离（Minimum Orbital Intersection Distance，MOID），在Hedo 等[6]提出的求解两椭圆轨道间MOID 的SDG（Space Dynamics Group）方法上进行改进，推导出可适用于双曲线轨道的MOID 计算公式。依据此理论基础，提出基于MOID 计算的小行星顺访探测目标预筛选方法，并以一条飞向日球层边缘的深空探测任务轨道方案作为仿真算例。仿真结果证实了预筛选操作通过减少需要轨道递推计算的小行星个数，降低了计算量，提高了顺访探测目标确定的效率[7]，并且由于MOID 计算公式对双曲线轨道的适用性，此方法也适用于飞往外太阳系等复杂轨道类型的探测任务。

1 最小轨道交叉距离求解

最小轨道交叉距离，指两天体密切轨道上最近两点之间的距离。此问题的研究可用于预报具有潜在危险的小天体与地球发生碰撞事件[8]和计算空间碎片撞击在轨航天器的概率[9]。

MOID 问题求解方法主要分为获得距离函数所有临界点的代数法[10-12]，迭代找到全局最小值的数值法[13,14]，以及代数与数值相结合的混合法[15]。文献[10]通过求解轨道近点角为变量的经典三角方程，得到两轨道间距离最小值；文献[11]将寻找两椭圆轨道间距离临界点问题转化为确定八次三角多项式的根的理论过程；文献[12]应用几何代数法搜索单变量16 次多项式实根，基于快速傅里叶变换给出两轨道间距离临界点。文献[13]巧妙利用两轨道间最小距离线的正交性迭代计算，评估小行星与行星间近距离接触概率；文献[14]提出一种快速的几何方法，但是求解的准确性与计算速度成反比；文献[15]采用一种主要通过在每个黄道子午面上一特定距离来近似轨道之间实际距离的数值方法，结合并行计算加快计算速度。

在上述研究背景下，2018 年Hedo 等[6]提出了SDG 方法，利用迭代法将空间内两个椭圆轨道之间最近距离的求解转化为求解其中一个椭圆上所有点与另一个椭圆之间的最近距离，可实现两共焦点椭圆轨道MOID 的快速准确计算。针对两个轨道中至少有一个轨道具有低偏心率的情况，Hedo 等[16]2020 年提出分别通过临界偏近点角和平方距离的偏心率渐进展开式进行计算的方法。

到目前为止，包含双曲线轨道组合的MOID 计算问题的相关研究工作较少，文献[17]提出了通过查找距离函数所有驻点，即查找16 次代数多项式方程所有根的方法，但是由于程序原因，算法会带来一定的数值误差。

在深空探测任务中，探测器有沿双曲线型轨道运动的情况。此时，双曲线轨道与椭圆轨道之间的最近距离无法直接通过SDG 方法求得。鉴于SDG 方法中算法的灵活性，本文基于圆锥曲线运动模型改进SDG 方法，推导出双曲线型轨道MOID 的计算公式。

1.1 椭圆形MOID 问题的SDG 方法

为便于描述，分别命名两天体的椭圆轨道中一个为基准椭圆，另一个为次要椭圆，二者称谓可互换。

SDG 方法可以概括为以下两个算法[6]。

算法1 计算空间中任意点与基准椭圆之间的最近距离。

算法2 基于算法1，计算次要椭圆上所有点与基准椭圆之间的最近距离，集合中最小值即为所求MOID。

执行算法前，需要将次要椭圆上的点坐标变换到基准椭圆所在坐标系内，此过程涉及以下三类坐标系。

（1）惯性坐标系Fx0y0z0。以两椭圆轨道公共焦点为坐标系原点，坐标轴满足右手定则，[i0,j0,k0]为对应的单位矢量。经典的轨道根数（包括轨道倾角ij和 升交点经度Ωj以 及近点幅角ωj）是参考这个坐标系给出的，这里j=1 对应基准椭圆，j=2 对应次要椭圆。

（3）基准椭圆的中心坐标系Ox1y1z1。以基准椭圆的几何中心为坐标系原点，坐标轴与基准椭圆轨道的近焦点坐标系Fp1q1h1坐标轴平行。二者定义以及相对位置关系如图1 所示。

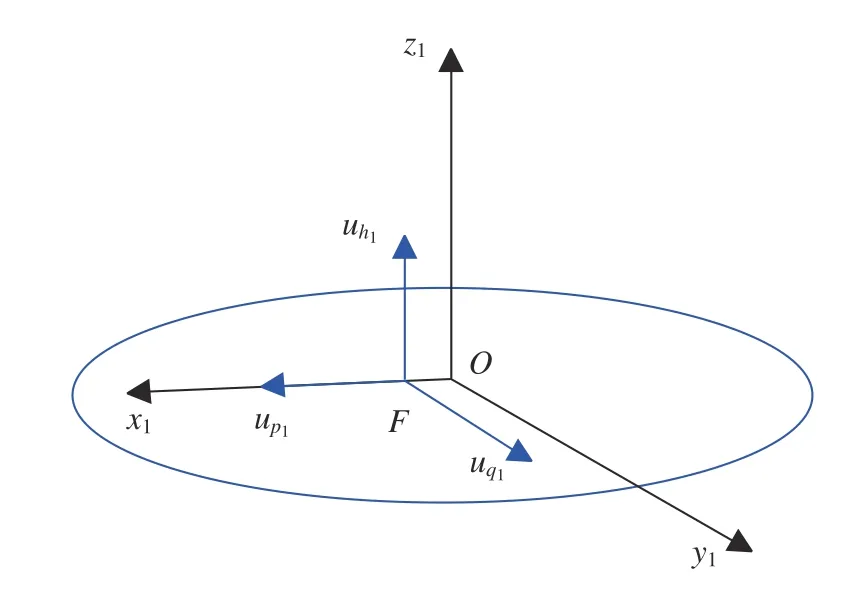
图1 基准椭圆近焦点坐标系与中心坐标系的空间位置关系Fig. 1 Position relationship between perifocal reference and central frame of primary ellipse

其中，RZ(α)为 绕坐标轴Oz顺时针旋转α弧度的旋转矩阵。

计算次要椭圆上的点E2与基准椭圆之间最近距离时，需将该点坐标转换到基准椭圆中心坐标系Ox1y1z1中 ，点E2对 应的位置矢量可表示为OE2=F E2+OF，各个分量为式中，a1和e1分 别为基准椭圆的半长轴和偏心率；a2，e2，u2分 别为次要椭圆的半长轴、偏心率和点E2对应的偏近点角。

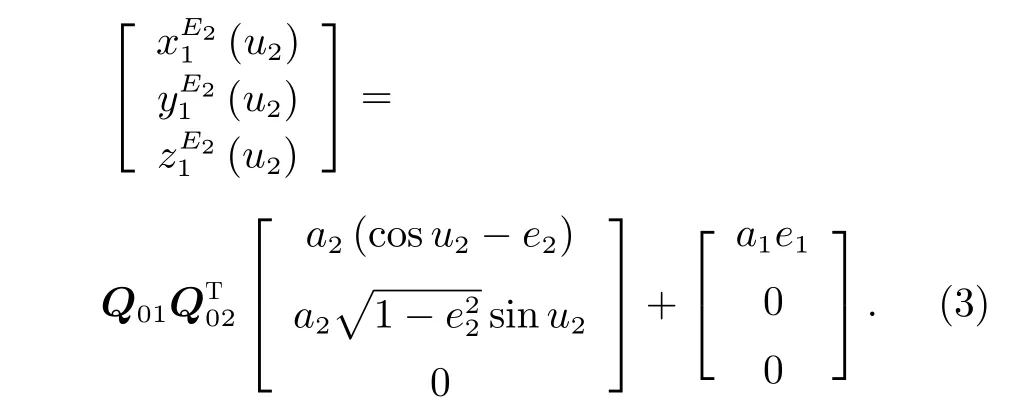
将空间中一点P0投影到基准椭圆所在平面，记投影点为P，则点P0到基准椭圆的距离被分解为两个正交方向的分量，即点P0到点P的垂直距离和点P到基准椭圆的距离。对于给定的点P0，其与基准椭圆所在平面的垂直距离固定，因此点P0至基准椭圆的最近距离求解可转化为投影点P至基准椭圆的最近距离求解问题。平面内一点与椭圆之间的距离如图2 所示。

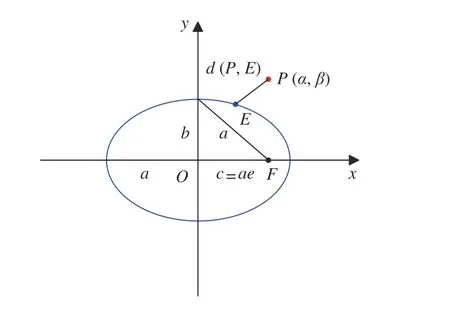
图2 平面内一点与椭圆之间距离Fig. 2 In-plane distances between an ellipse and a coplanar point

在基准椭圆中心坐标系Ox1y1z1中，Ox轴、Oy轴分别与基准椭圆的长轴和短轴重合，基准椭圆关于Ox轴和Oy轴对称。因此，求解投影点P与基准椭圆之间最近距离时，只对投影点P在第一象限的情况进行讨论，落在其他象限的情况可根据椭圆对称关系获得。

用a，b，e分别表示基准椭圆的半长轴、半短轴和偏心率。用偏近点角u描述基准椭圆轨道上点E(x,y)的坐标，有式中满足c=ae。

当基准椭圆为圆形，或者投影点P落在坐标轴Ox或Oy轴上时，距离极小值有解析解。表1 列出了这几种特殊情况下的距离极小值解，表1 中xE′和yE′分 别表示距离为极小值dE′时对应的基准椭圆上点E′的横纵坐标，uE′为该点的偏近点角。

表1 平面内一点与椭圆之间最近距离的封闭解情况Table 1 Cases of minimum distance between an ellipse and a coplanar point with closed-form solution

当投影点P落在第一象限内（α ＞0,β ＞0）时，极值条件式（6）没有封闭解，需通过多项式求根或数值迭代法求解极值条件。在满足求解精度情况下，数值迭代法的计算效率更高，迭代算法采用高度收敛的Halleys 方法[18]，迭代增量为

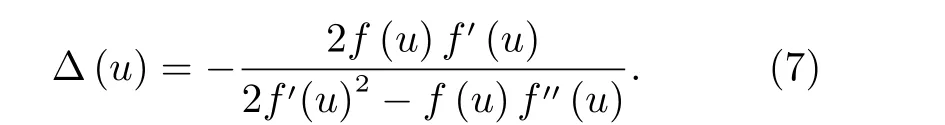
算法迭代计算的条件为

Δ(u)／=0⇒f(u)f′(u)／=0，迭代终止条件为

Δ(u)=0⇒f(u)f′(u)=0。f′(u′)=0f(u′)／=0u′

而当 ， 时，由于 不是方程的根，迭代不应停止，为避免此情况下迭代终止，增加判断

1.2 双曲线型MOID 问题的求解方法

鉴于SDG 方法应用场景的局限性以及求解方法的高效性，将该方法求解思路借鉴到双曲线轨道MOID 求解中，针对不同的轨道类型，改进相应计算公式。

当基准轨道为椭圆而次要轨道为双曲线时，双曲线轨道上点H2坐标转换到基准椭圆中心坐标系Ox1y1z1中 ，该点对应的位置矢量表示为OH2=F H2+OF，式（3）中各分量的表达式可以转化为

当双曲线轨道作为基准轨道时，SDG 方法的计算公式将不再适用，算法1 需要计算平面内点到达双曲线（一支）的最近距离。

为描述方便，将基准天体双曲线轨道称为基准双曲线，并认为基准双曲线轨道位于左支，太阳位于左焦点，双曲线轨道的定义如图3 所示。

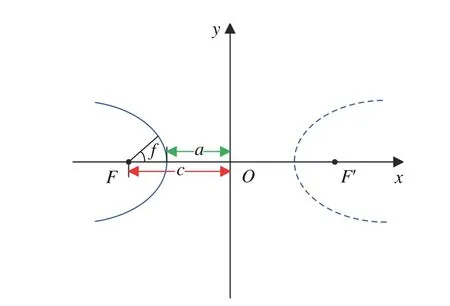
图3 探测器相对于中心天体（焦点F）的双曲线轨道Fig. 3 Hyperbolic orbit of the spacecraft relative to the central body ( focus F )

在此约定下，基准双曲线中心坐标系Ox1y1z1中，次要椭圆上点E2的 位置矢量为OE2=F E2+OF，各分量为

基准双曲线的对称轴与中心坐标系的Ox轴平行，焦点F位于Ox轴负半轴，分别用a，b表示基准双曲线的半长轴与半短轴。用偏近点角u表示基准双曲线上点H(x,y)的坐标分量，有

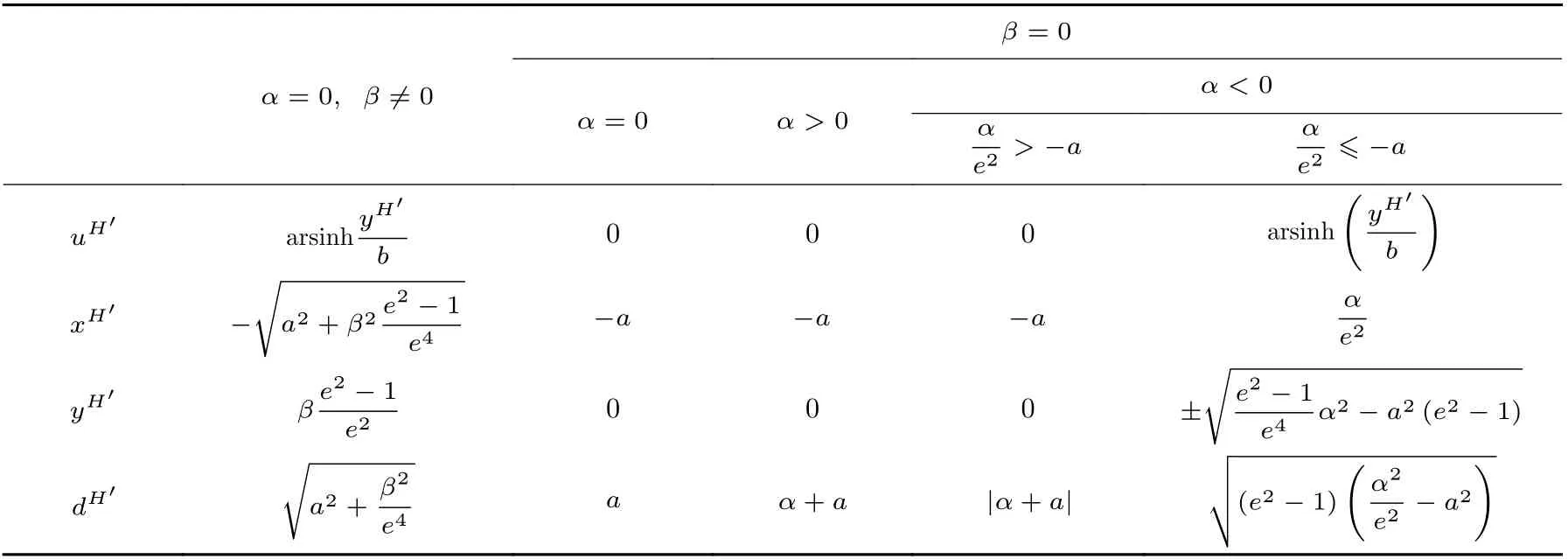
表2 平面内一点与双曲线（左支）之间最近距离的封闭解情况Table 2 Cases of minimum distance between a hyperbola (left branch) and a coplanar point with closed-form solution

综上，结合SDG 方法对基准轨道为椭圆的讨论，以及本工作中针对基准轨道为双曲线讨论的两种情况，可以实现对基准轨道类型为椭圆或双曲线，次要轨道类型为椭圆或者双曲线的MOID 问题进行快速准确求解。

1.3 结果验证

文献[19]可以对任意一对椭圆轨道之间的最小轨道交叉距离进行计算。为检验编写程序的正确性与精确度，将计算结果与文献[19]的结果进行比较。表3 中记录了几组轨道算例的结果，其中椭圆轨道根数依次为半长轴、偏心率、轨道倾角、升交点经度、近点幅角。半长轴单位为AU（Astronomical Unit），角度单位为度。为与本工作中的计算结果进行区分，将文献[19]中MOID 结果标记为MOID 参考值。

表3 结果显示，所编写程序的计算结果与文献[19]结果的误差率不超过1.1×10–5%，可证实计算程序和算法的正确性。对于包含一条双曲线轨道的MOID 计算，分别以该双曲线轨道为次要轨道和基准轨道两种方式进行计算，并将两种计算结果列于表4。表3 和表4 中轨道根数的记录顺序为半长轴（单位AU）、偏心率、倾角（单位°）、升交点经度（单位°）、近点幅角（单位°）。表4 中结果验证了求解双曲线轨道MOID 计算公式的正确性与计算精度。

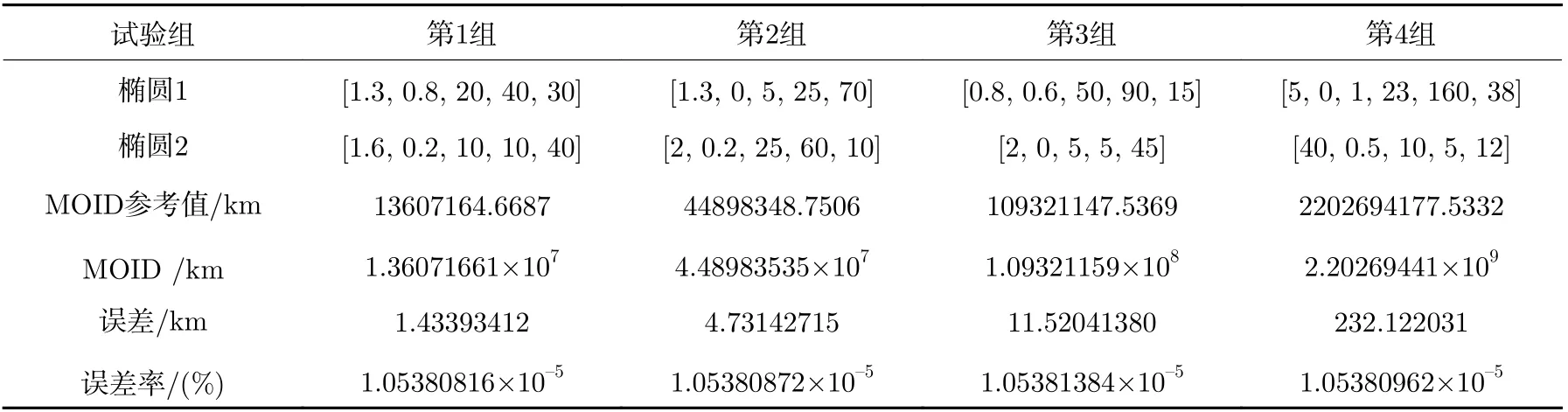
表3 椭圆轨道间MOID 计算结果Table 3 Calculation results of MOID between ellipses

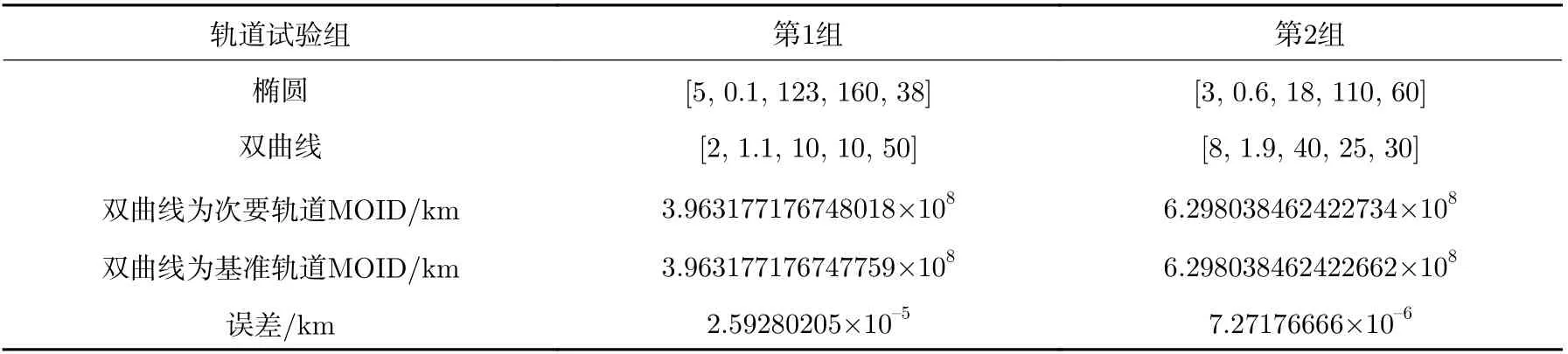
表4 椭圆轨道与双曲线轨道间MOID 计算结果Table 4 Calculation results of MOID between ellipse and hyperbola

2 基于MOID 计算的小行星顺访探测目标预筛选方法

将空间内两条轨道之间的最小轨道交叉距离应用到小行星顺访探测目标的预筛选问题中，计算小行星和探测器轨道之间的最小轨道交叉距离，与设定的可接近标准进行比较：如果MOID 大于可接近标准，说明二者相对距离大于顺访探测的距离要求，从探测目标群中淘汰该颗小行星；如果MOID 小于可接近标准，小行星和探测器之间可达到的真实最近距离可能满足接近标准，需保留进行下一步轨道递推求解二者相对距离。

由此，基于MOID 计算的小行星顺访探测目标确定可通过如下6 个步骤实现（见图4）。

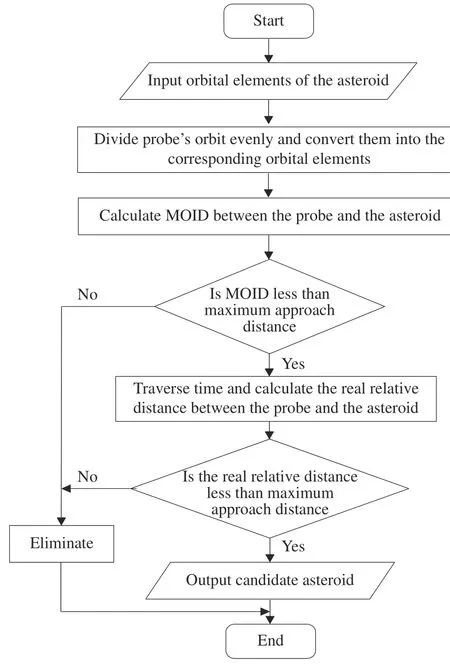
图4 基于MOID 计算的小行星顺访探测目标筛选流程Fig. 4 Screening process of asteroid follow-up exploration targets based on MOID calculation

第一步 确定探测器飞越小行星活动区域的轨道与相应的飞行时间。

第二步 将探测器轨道平均划分为n段，记节点时间为ti， 每一点的位置速度矢量分别记为r(ti)，v(ti)， 其中i=1,2,...,n。

第三步 由于探测器轨道可能是开普勒轨道与非开普勒轨道的组合，因此将每一节点的位置速度矢量转为该点吻切轨道的轨道根数，以小行星轨道为基准轨道，探测器轨道为次要轨道，遍历时间节点计算二者MOID 值，MOID 值集合中的最小值即为这一段探测器轨道与该颗小行星轨道之间的几何最近距离。

第四步 对所有小行星进行第三步计算，保留几何最近距离小于所设定可接近标准的小行星，完成预筛选过程。

第五步 对于从预筛选步骤中保留下来的小行星，通过轨道递推计算每一时间节点上的位置矢量，记为rj(ti)，其中j为小行星编号。

第六步 判断探测器与小行星的距离是否满足设定的接近标准，如果满足，则作为目标候选星，否则舍弃。

3 仿真算例

以一条2026 年发射飞往日球层边缘的脉冲轨道作为仿真算例。探测器从地球逃逸后，经金星－地球－地球借力（Venus-Earth-Earth Gravity Assist，VEEGA）飞往木星，随后经木星、海王星借力飞往日球层尾部方向（黄经为79°，黄纬为–5°）。针对探测器在海王星借力后飞至日球层边缘[20]段轨道进行小行星顺访探测轨道设计，对应的小行星群体主要是位于海王星轨道之外的外海王星天体（Trans-Neptunian objects，TNO）。探测器整段轨迹的详细参数列于表5。

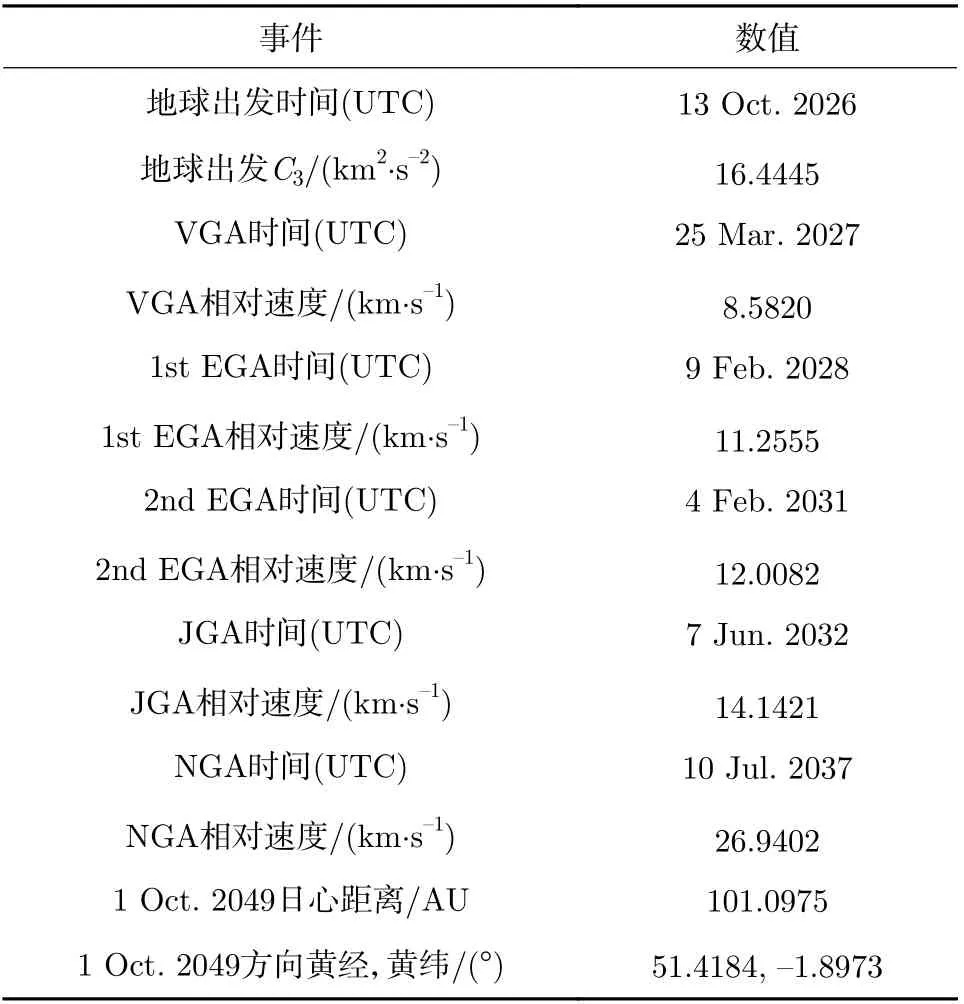
表5 仿真算例轨道详细参数Table 5 Detailed parameters of simulation example

从国际天文联合会（International Astronomical Union，IAU）的小天体中心（Minor Planet Center，MPC）网站[21]下载得到2503 颗外海王星天体的轨道数据，仿真中以太阳中心引力二体模型递推计算小行星位置速度矢量[22]，在真实的太阳系动力学环境中，一些小行星（例如近地小行星、半人马天体）所受摄动较大，简单的二体模型可能导致小行星状态计算有偏差[23]。为检验所提出小行星探测目标预筛选方法的效率与正确性，这里作此简单处理，后续在进一步选择探测目标、设计轨道方案时应对力学环境进行完整建模。探测器经海王星借力飞行近4500 天后距日心101 AU，针对此段轨道设置1 天的时间步长，标称轨道被划分为4467 个节点。仿真实验的硬件环境为Intel(R) Core(TM) i7-5557 U CPU @ 3.10 GHz，8 GB 内存， 64 位IOS 系统。设置不同的小行星顺访探测可接近标准，分别用基于MOID 计算的目标预筛选方法和直接轨道递推的传统筛选方法进行计算，相应计算时间列于表6。

由表6 中结果可以看出，仿真算例中预筛选操作将计算时间大幅缩短，当可接近标准为2×108km 时，预筛选方法所需计算时间不到传统方法计算时间的1/3，基于MOID 计算的小天体顺访探测目标预筛选操作有效提高了小天体探测目标确定效率。由于外太阳系空间尺度比较大，2×108km 的可接近标准在此任务轨道中是合理的，依此标准先筛选出部分目标，再微调轨道，最终可以实现消耗不多的速度增量近距离飞越小行星。表7 给出接近距离小于2×108km的小行星，图5 为探测器接近小行星状态。

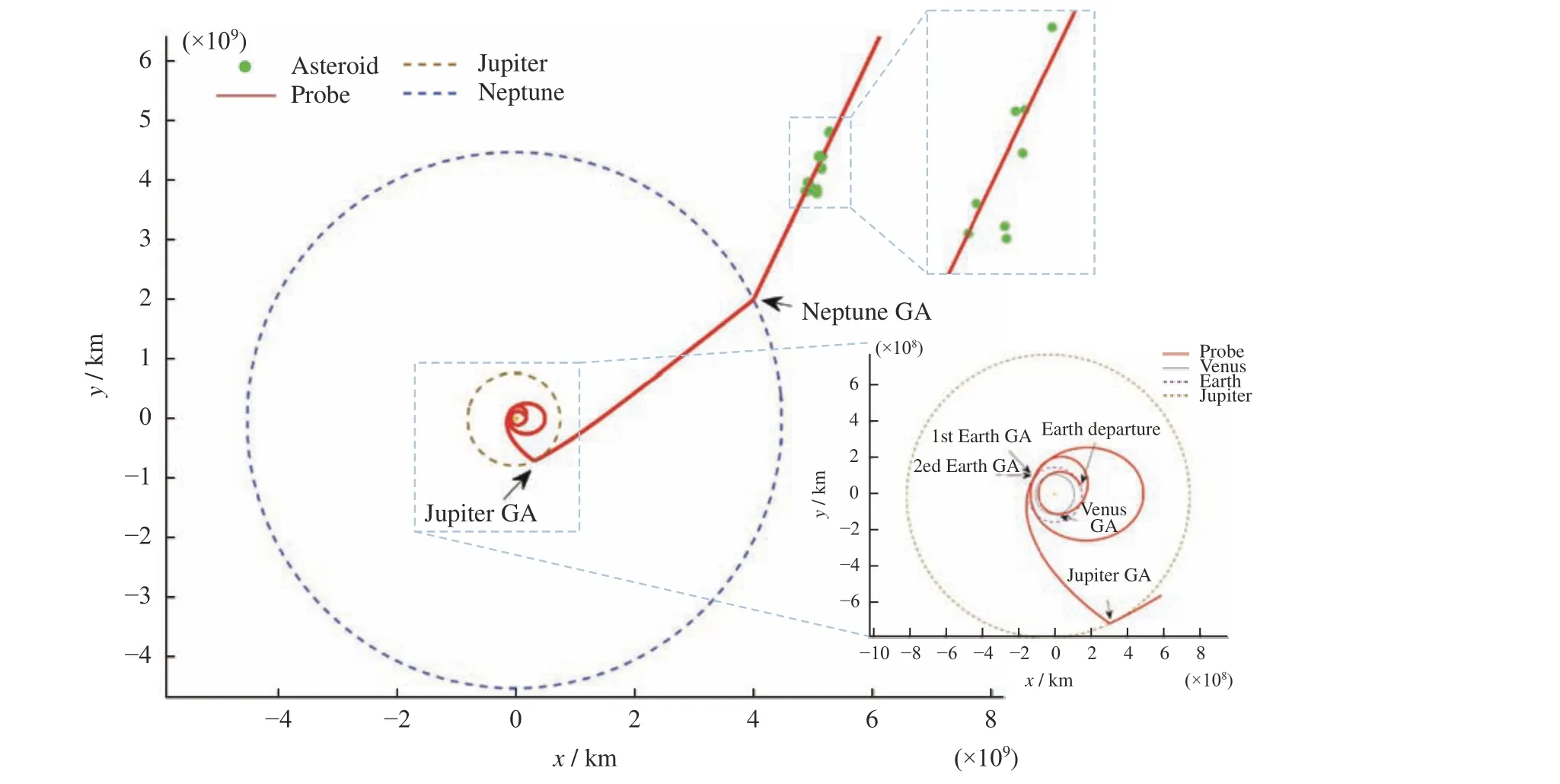
图5 探测器飞越小行星搜索状态Fig. 5 Search results of TNOs flyby

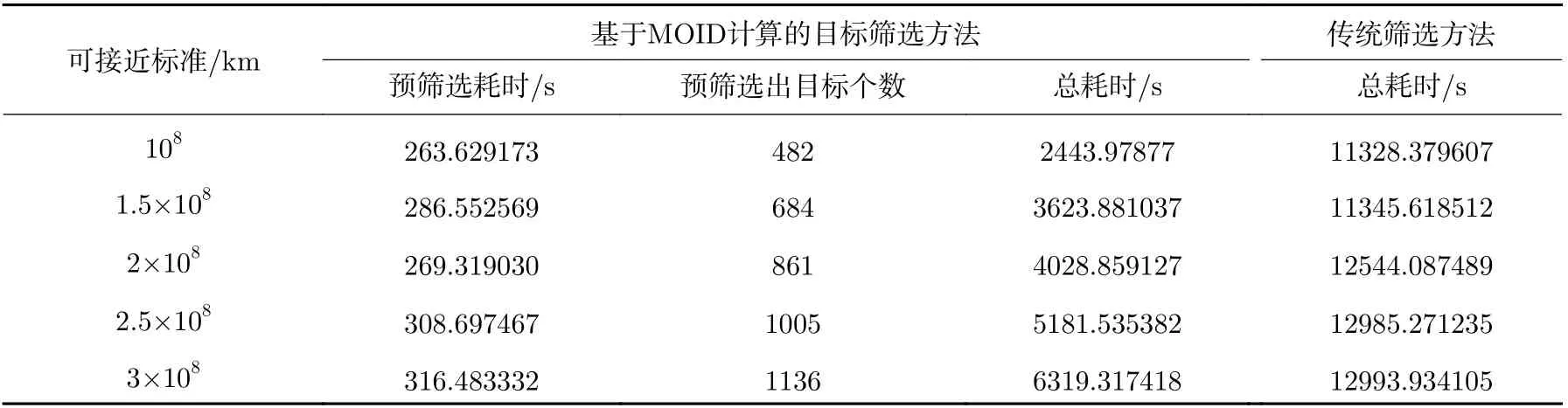
表6 小行星顺访探测目标筛选计算时间Table 6 Calculation time of asteroid follow-up exploration targets screening

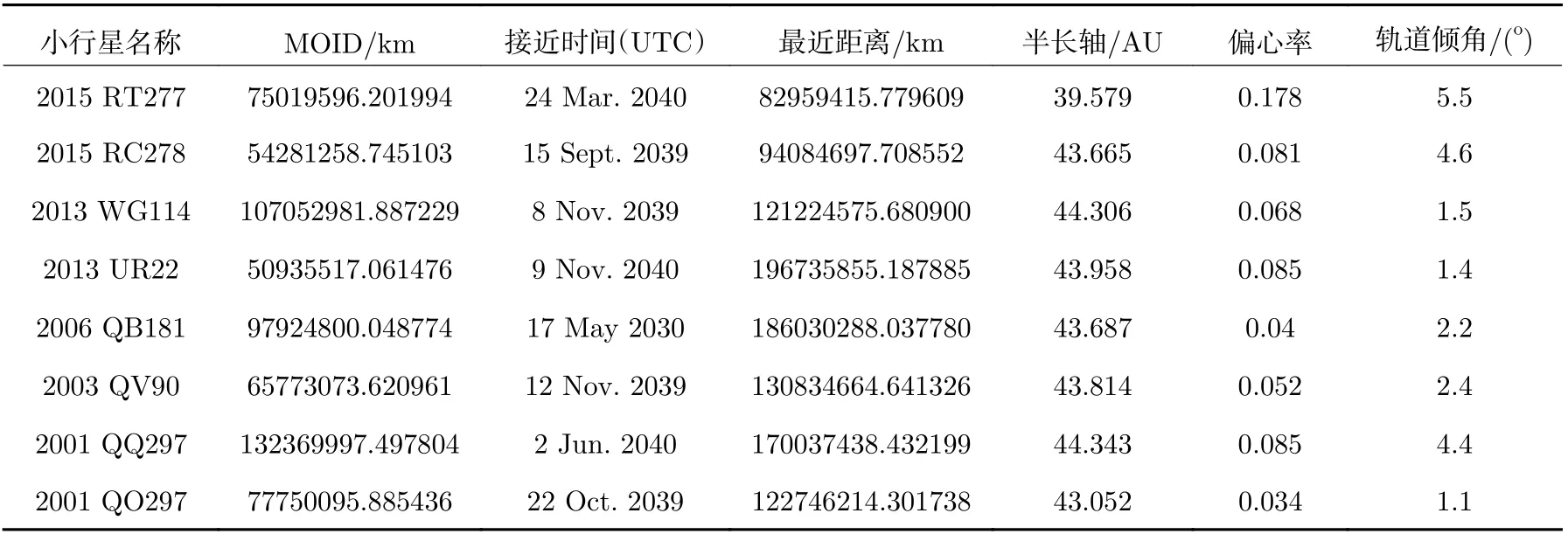
表7 接近距离小于2×108 km 的小行星Table 7 Approaching asteroids less than 2×108 km away

筛选得到飞越目标后，从搜索结果中选择一颗或几颗小行星作为飞越目标，重新优化设计探测器在海王星至日球层边缘的飞行轨道。一般设计流程为：基于圆锥曲线拼接模型[24]进行轨道初步设计，在日心飞行段只考虑太阳引力，当探测器与行星日心位置相同时进行借力飞行[25]，与小行星日心位置相同时即认为飞越小行星；在轨道精确设计阶段，以初步设计结果作为初值，考虑观测、成像条件和探测器实际机动能力、受力情况及小行星真实力学环境等具体因素，详细设计飞越小行星的轨道。

4 结 论

针对小行星顺访探测目标确定问题中，遍历小行星和时间节点计算探测器与小行星之间最近距离时计算量大、效率低的缺点，推导了适用于双曲线轨道最小轨道交叉距离计算的公式，提出了基于 MOID的小行星顺访探测目标预筛选方法，主要结论如下。

（1）双曲线轨道MOID 计算公式的推导拓展了MOID 问题在轨道设计的应用场景。

（2）提出基于 MOID 计算的小行星顺访探测目标预筛选方法，减少了对整个小行星群体遍历个体和时间节点求解探测器与小行星相对距离的计算量，节省了计算时间，提高了小行星顺访探测目标确定的效率。

（3）以一条运行近4500 天的标称轨道为仿真算例，设置时间步长为1 天，从2503 颗外海王星天体中筛选顺访探测目标，当可接近标准设置为2×108km时，基于MOID 计算的预筛选方法耗时不到传统方法计算时间的1/3。