CYGNSS 海面风速固有误差与时空分布特征*

刘 帅 林文明 鲁云飞

(南京信息工程大学海洋科学学院 南京 210044)

(国家卫星海洋应用中心 北京 100081)

0 引言

利用全球导航卫星系统在地球表面的反射信号（Global Navigation Satellite System Reflectometry，GNSS-R）进行地表物理参数监测是一种新兴的遥感技术。其是通过低轨卫星或飞机上搭载的多普勒接收机接收GNSS 卫星从地球不同类型表面反射的L波段微波信号，反演海洋表面高度、风速、盐度、土壤湿度、海冰特征、积雪结构以及河口微小塑料浓度等地球物理参数[1—5]，具有全天候、近实时、高精度的特点[6,7]。其中海面风速监测是GNSS-R 最主要的应用之一。

2003 年英国萨普公司发射的灾害监测星座（Disaster Monitoring Constellation，UK-DMC）率先证明了GNSS-R 监测海面风速的可行性，其反演风速与浮标测量风速基本一致[8]。2014 年7 月英国发射的（TechDemoSat-1，TDS-1）卫星进一步验证了GNSS-R 监测海面风速的能力，最大反演风速约为28 m·s—1[2,9]。2016 年7 月美国航空航天局发射的气旋全球导航卫星系统（Cyclone Global Navigation Satellite System，CYGNSS）是目前规模最大、发展最成熟的GNSS-R 遥感星座。CYGNSS 由8 颗小卫星组成，空间分辨率约为5～50 km，风速监测动态范围小于70 m·s—1，误差约为2 m·s—1[3,10—13]。中国在 2019 年6 月5 日发射了捕风一号和二号科学试验卫星，其风速遥感精度满足2 m·s—1或10% 的设计要求。2021 年中国风云三号E 卫星搭载的全球导航卫星掩星探测仪-II 兼具GNSS-R 观测能力，将进一步提高中国在GNSS-R 领域的水平。

近10 年来，GNSS-R 海面风速遥感研究不断深入，已开展了大量的系统定标、风速反演以及真实性检验等研究。TDS-1 卫星在没有校准的情况下，风速在3～18 m·s—1区间范围内的反演误差只有2.2 m·s—1[14]；Giuseppe 等[15]证明了GNSS-R 对于风速大于7 m·s—1的海面风遥感不是最佳的，但是考虑到整个海洋中大约一半的风速值在0～7 m·s—1范围内，在这个范围内进行准确的反演是可行的；Clarizia 等[9,16]提出了一种基于最小方差的风速估计方法，该方法利用GNSSR 延迟多普勒图像的五个参数获得的风速组合，其均方根误差低于单参数反演的均方根误差；Lin 等[5]提出了一种改进TDS-1 风速的地球物理模型函数（Geophysical Model Function，GMF）综合方法，通过校正接收机天线增益和未知的发射机天线增益，显著降低了测量信号的不确定性；Huang 等[4]使用完整的延迟多普勒图像进行风速反演，显著提高了风速的反演精度，但是在高风速区域，这种方法仍然受涌浪、观测偏差、反射点误差和基尔霍夫几何光学模式误差的影响。2002 年中国科学院遥感与数字地球研究所开始开展GNSS-R 海面风场反演的研究工作，并在南海和黄海海域进行了大量的实验[17]。Yuan 等[18]利用Elfouhaily 海浪谱模型，数值模拟了机载高度下散射信号相关功率的理论波形，并结合机载实测数据开展风速反演研究，得到的风速与浮标参考风速相差1.4 m·s—1；Luo 等[19]结合机器学习树算法模型反演海面风场，风速反演误差小于2 m·s—1；Lyu 等[20]根据一维时延相关功率曲线和观测量建立风场反演模型，得出风速的反演误差为2.02 m·s—1。

以往大部分研究主要关注GNSS-R 海面风速反演的整体误差特性，而对GNSS-R 遥感风速的时空变异特性和固有误差的研究较少。特别是由于GNSS发射机的发射功率和天线增益不是精确的已知值，而且可能随着时间变化，使得GNSS-R 接收信号与海面风速的对应关系存在一定程度的不确定性，进而导致反演的海面风速精度较差且缺乏时空分布的一致性[21]。因此，GNSS-R 风速遥感数据尚未得到广泛应用，特别是在对误差定量化需求程度较高的数值预报模式中的应用。本文以CYGNSS 风速数据为例，参考传统微波散射计海面风场误差分析方法，详细研究了CYGNSS 风速的时空分布特征和固有误差特性，旨在揭示CYGNSS 遥感风速的误差规律，为CYGNSS 和其他GNSS-R 任务的风速数据应用提供借鉴。

1 数据与分析方法

1.1 数据说明

利用NASA 发布的CYGNSS 二级（L2）数据（3.0 版本）开展研究，并使用同期全球锚定浮标的现场观测数据和欧洲中期天气预报中心（ECMWF）的预报风场数据作为验证参考数据，所有数据时间均为2019 年。ECMWF 风场的时间分辨率为3 h，空间分辨率为0.125°×0.125°，因此首先通过空间双线性插值获取CYGNSS 观测位置的三个连续时刻的ECMWF 风速值，再利用时间维的样条插值获取CYGNSS 观测时刻的ECMWF 风速。这里的三个时刻是指ECMWF 预报风场的时间，选取的标准一是离ECMWF 的分析时刻最近，二是完全涵盖CYGNSS 的观测时间。通常是两个时刻在CYGNSS观测之前，一个在后。随后利用拉依达准则分别对CYGNSS 风速、ECMWF 风速、浮标风速进行如下质量控制。

（1）计算不同对应样本（CYGNSS 风速、ECMWF风速、浮标风速）的平均值

其中，n代表该样本中数据的总数，i代表该样本中数据的序数，Wi代表该样本中第i个数据。

根据拉依达准则，假设一组检测数据只含有随机误差，对其进行计算处理得到平均值和标准偏差如果超过这个区间的误差，就不属于随机误差而是粗大误差，则将含有该误差的数据予以剔除。 这种判别处理原理和方法仅局限于样本数据符合正态或近似正态分布（风场分量域的概率分布近似为对称高斯分布）。拉依达准则要求测量次数充分大，测量次数少的情形采用拉依达准则剔除粗大误差是不可靠的。本文的实验数据大约为3.5 亿组，其中匹配后的CYGNSS 和ECMWF 数据约为3.5 亿组，由于全球锚定浮标数据量有限，匹配后的CYGNSS 和 ECMWF 浮标数据约为6 万组，基本符合拉依达准则。

由于浮标风力计的高度不等，需要利用LKB 模型将所有的浮标风速转换成10 m 高度的等效中性风，然后将上述CYGNSS 和ECMWF 匹配的数据集与浮标进行配对[22]。考虑CYGNSS 的观测轨迹与卫星高度计类似，浮标匹配规则设定为空间距离小于50 km，时间差异小于1 h。

1.2 分析方法

研究CYGNSS 遥感风速及其误差的时空分布特征，具体内容包括： CYGNSS 遥感风速的气候态特征，特别是一定时间范围风速的变异性（Variability）特征，并与ECMWF 风速特性对比，从而了解CYGNSS 风速的动态范围与尺度特征； CYGNSS 与ECMWF 风速差异的时空分布特征，从而了解CYGNSS 风速偏差和精度时空变化规律。考虑CYGNSS 由8 颗卫星组成，不同卫星之间的风速可能存在偏差（见图1），因此需要针对不同卫星的数据分别进行分析。

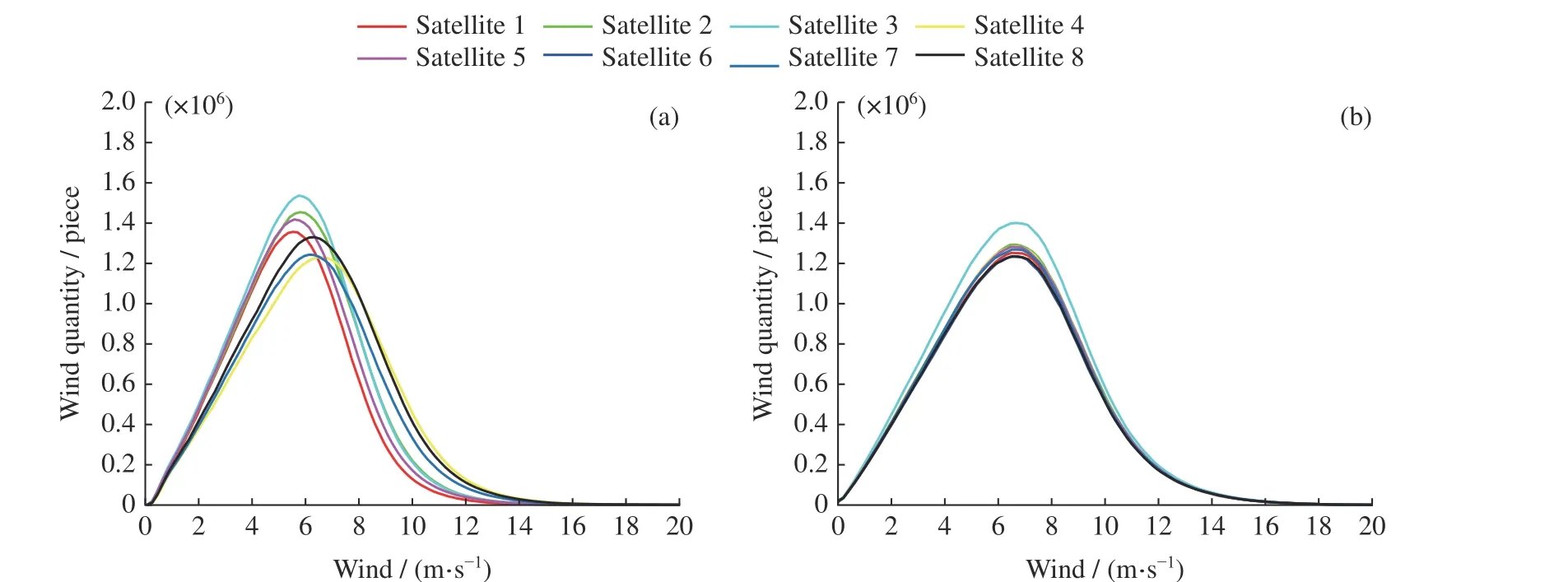
图1 CYGNSS 不同卫星的风速（a）及匹配的ECMWF 风速（b）曲线Fig. 1 Wind speed curve for different CYGNSS satellites (a), and the matched ECMWF wind speed (b)

由于真实海面风速是未知的，使用任何一种参考数据对遥感数据进行真实性检验都无法定量估计遥感数据自身固有误差。这里固有误差指各种数据源的测量方差，其等同于均方根误差，用来衡量观测值与真值之间的偏差。例如，CYGNSS 与ECMWF 风速差异的方差实际上是两者固有误差共同作用的结果。Stoffelen[23]等提出一种三配对数据分析和标定方法，广泛用于卫星遥感海面风场、盐度、降雨率等数据的真实性检验。本文对该方法进行简化，并用于估计CYGNSS 风速的固有误差。假设不同系统获取的风速值和真实值之间存在线性关系，那么数据集中的每种数据能够表达为

其中，x，y，z分别表示浮标、CYGNSS 和ECMWF 的风速值;T表示真实值;e1，e2，e3为各种风速遥感/预报系统中存在的随机误差（均值为0）;α1，α2，α3和β1，β2，β3为各种数据与真值的线性回归系数。

通常不同数据的误差是不相关的， 即〈e1e2〉=〈e1e3〉=〈e2e3〉=0，并且与T也是非相干的，即〈Te1〉=〈Te2〉=〈Te3〉=0 ， 其中〈·〉算符表示变量的数学期望值。计算x，y，z的混合二阶矩并联立方程组，可以消去未知的变量T，得到

同时可以得到每种风速的固有方差（即标准差的平方）

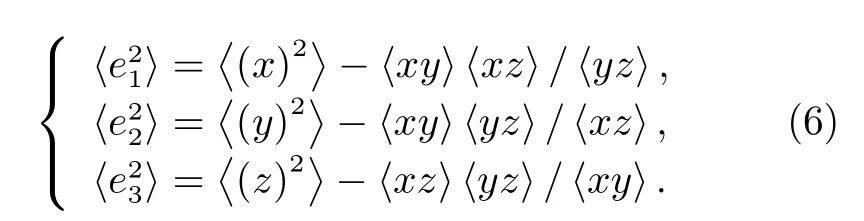
以及偏差校正系数

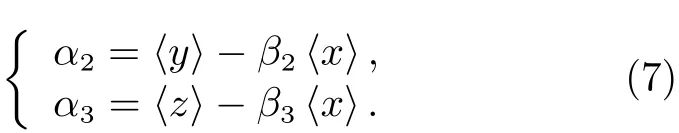
需要注意的是，6 个系数中只有4 个可以用x，y，z导出，因此需要定义一个观测值（例如x）作为参考，进而估计其他两组数据的偏差校正系数和比例因子α2，α3，β2，β3。由于浮标现场观测的风速通常更加准确，因此假定x为真实值，即α1=0，β1=1，代入式（5）和（7）可得GYGNSS 和ECMWF 的偏差校正系数和比例因子。

2 结果与讨论

2.1 GYGNSS 风速的时空变异性

风速在一定时间范围内或空间范围内的变化特性称为时空变异性，通常用相应数据集的标准差来定量描述。图2(a) 给出了CYGNSS（红色曲线）与ECMWF（蓝色曲线）风速的标准差随月份的变化。可以看出，CYGNSS 风速与匹配的ECMWF 预报风速的时间变异性趋势一致，即夏冬两季（12－2 月、6－8 月）变异性较强、春秋两季（3－5 月、9－11 月）变异性较弱。总体而言，CYGNSS 对海面风速变化的捕捉能力弱于ECMWF 预报模式，与图1 所示的两种风速分布一致，主要原因是GNSS-R 测量信号对中高风速的敏感性较低。图2（b）进一步对比了CYGNSS 8 颗卫星反演风速的时间变异性。可以看出，所有卫星的风速变异性趋势基本一致，但不同的CYGNSS 卫星对海面动态变化的刻画能力不一样，即第4，7，8 颗卫星的风速变异性明显大于其他卫星的值。考虑各个卫星在1 个月内对全球的覆盖范围基本一致，这种差异的主要来源可能在于传感器或数据处理本身，而不是地球物理状态的变化，例如不同卫星的测量信号定标之后仍存在一定程度的不一致。

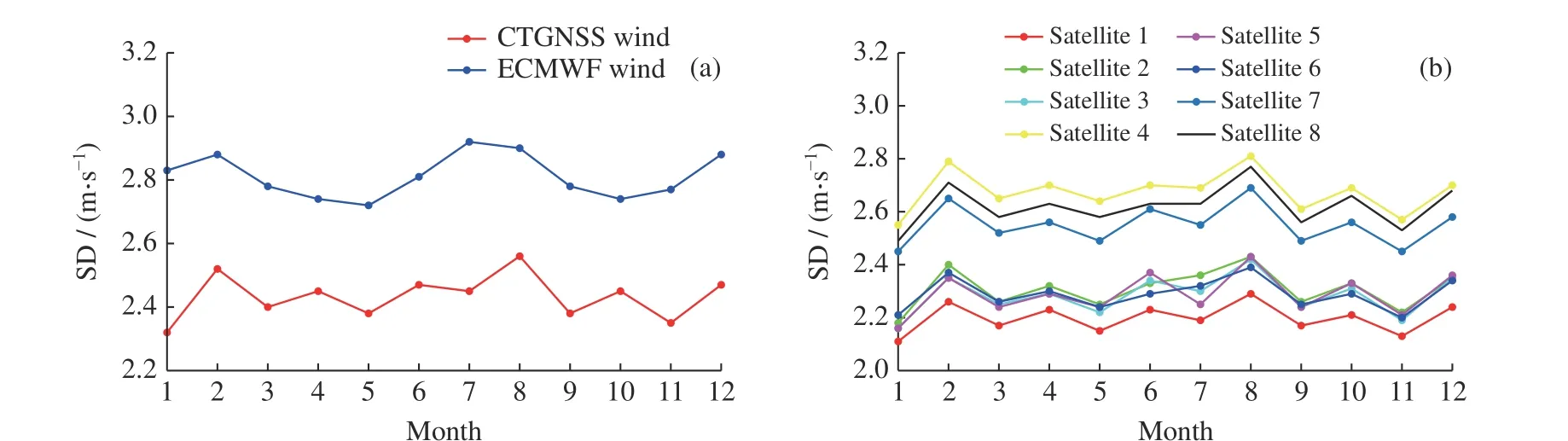
图2 CYGNSS 和ECMWF 风速的变异性（标准差）随月份的变化（a）及CYGNSS 8 颗卫星的风速变异性（b）Fig. 2 Monthly wind variability (Standard Deviation, SD) of CYGNSS and ECMWF (a),wind variability for the eight CYGNSS satellites (b)

图3 对比了CYGNSS 和ECMWF 年平均风速的全球空间分布以及相应的风速标准差（每个格点位置1 年之内所有风速样本的标准差）。可以看出，CYGNSS 和ECMWF 年平均风速的空间分布基本一致，但前者对东太平洋热带辐合带的低风速区和西风带的较高风速区的细节描绘明显不如后者清晰。此外，由于现有的GNSS-R 传感器对高风速的敏感性普遍较差，CYGNSS 在西风带区域、好望角、阿拉伯海以及西北太平洋的风速变异性明显小于ECMWF。

图3 CYGNSS（a）和ECMWF（b）年平均风速的空间分布，其风速变异性（不同网格点范围内风速的标准差）的空间分布（c）（d）（网格的大小为0.125°×0.125°）Fig. 3 Geographic distribution of the annual mean wind speed for CYGNSS (a) and ECMWF (b). The spatial distribution of wind variability for CYGNSS (c) and ECMWF (d) (Standard Deviation of wind speed in different grid points) (Grid size is 0.125°×0.125°)

2.2 CYGNSS 与ECMWF 风速差异的时空分布特征

以ECMWF 风速为参考，研究CYGNSS 风速偏差的时空分布特征。图4（a）给出了CYGNSS 相对于ECMWF 的风速偏差随月份的变化。总体而言，7 月份偏差最大、1 月份次之，10 月份偏差最小，其他月份偏差差别不大。图4（b）进一步对比了不同卫星的风速偏差随时间变化的趋势。可以看出，所有卫星的风速偏差趋势基本一致，说明各卫星的GNSS-R 传感器测量信号具有较好的相对一致性。但不同卫星的风速偏差差异显著，第4，7，8 颗卫星的风速偏差明显小于其他卫星的风速偏差，这一点与图1 和图2 的现象相似，说明不同卫星之间的绝对定标仍有改善的空间。

图4（c）和（d）分别给出了CYGNSS 与ECMWF风速差异的整体标准差和每个卫星的标准差。与2.1 节类似，夏冬两季两者风速的差异较大，春秋两季则差异较小。需要注意的是，这种差异（偏差或标准差）不能直接用来表征CYGNSS 遥感风速的固有误差，因为其是CYGNSS 和参考风速（ECMWF）两者误差共同作用的结果。

图5 给出了CYGNSS 相对于ECMWF 的风速偏差及标准差的空间分布。可以看出，在高风速区域（例如西风带，见图3），风速偏差可达—2 m·s—1，这与GNSS-R 测量信号对高风速的不敏感性相一致；而在东太平洋的热带辐合带区域（低风速区），风速偏差基本大于2 m·s—1。总体而言，不同地理位置的自然风速大小不一样，导致了CYGNSS 反演风速的偏差也不一样。但是CYGNSS 与ECMWF 风速差异的标准差并没有呈现明显的随空间（在开阔大洋位置）变化而变化的特征，一定程度上说明CYGNSS 风速数据具有较好的精度一致性。图5（b）给出了在北海道渔场附近的风速标准差，可以看出该标准差较大，这可能是因为此处千岛寒流和日本暖流相遇，进而产生较为复杂的海面波浪状态，导致CYGNSS 反演风速误差较大。在人为活动较多的近海岸附近，GNSS-R 接收信号更容易受到电磁干扰或海面溢油等因素的影响，可能会造成反演风速的标准差较大。对CYGNSS 不同卫星的风速偏差和标准差（相对于ECMWF）进一步分析，发现第4，7，8 颗卫星反演风速的标准差明显大于其他卫星，尤其是西北太平洋和东太平洋的北半球区域。结合图2（b）和图4（b）可知，实际上很难判定第4，7，8 颗卫星风速数据的质量，因此需要通过三配对分析法评估CYGNSS 风速的固有误差，才能获取更准确的信息。

图4 （a）所有卫星CYGNSS 和ECMWF 风速差异的均值,（b）不同卫星风速偏差随月份的变化，（c）CYGNSS 和ECMWF 风速差异的标准差,（d）不同卫星风速的标准差随月份的变化。(参考风速为匹配的ECMWF 预报风速)Fig. 4 Monthly distribution of CYGNSS wind speed bias for all satellites data (a) and each individual satellite (b). (c) (d) are as same as (a) and (b), but for the standard deviation of the wind speed difference between CYGNSS and ECMWF

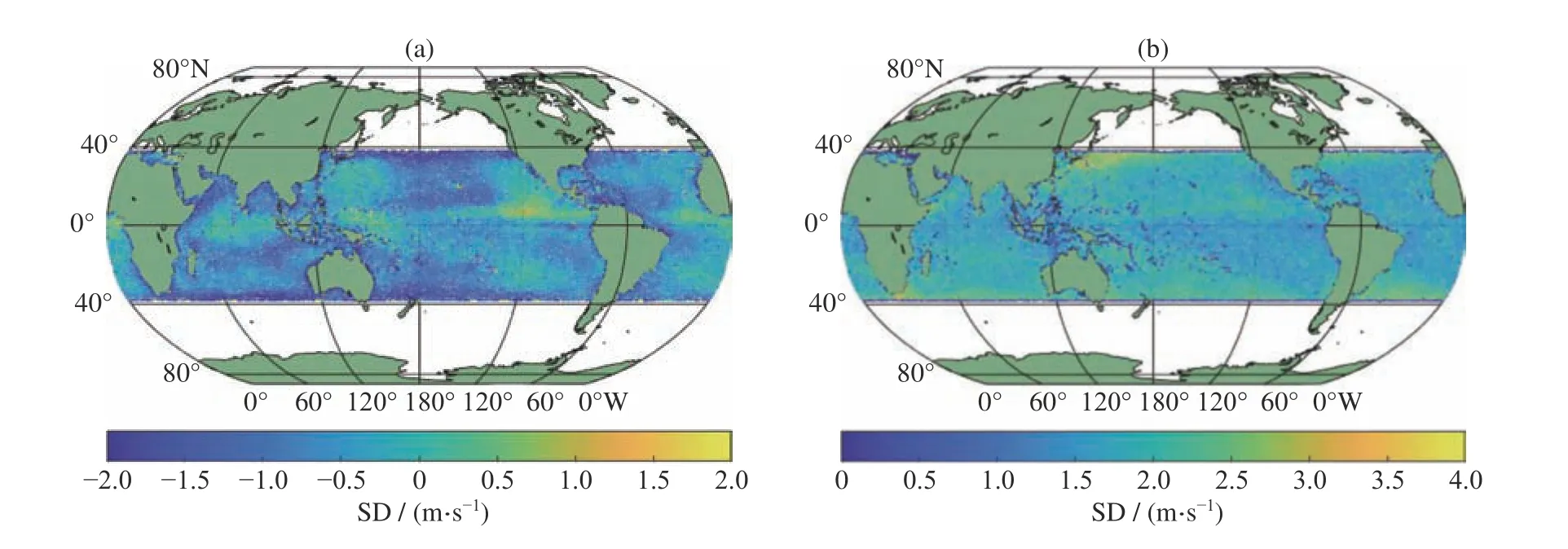
图5 CYGNSS 与ECMWF 风速差异的均值（a）及标准差（b）的空间分布Fig. 5 Geographic distribution of the CYGNSS wind speed bias (a) and Standard Deviation (SD) ECMWF (b)

2.3 CYGNSS 固有误差

图6 给出了CYGNSS、浮标以及ECMWF 风速两两对比的散点密度。浮标原始风速值是自然数，将其转换为10 m 高度处的风速后仍存在明显的离散特性，如图6(a) 和(b) 所示。可以看出，浮标与ECMWF 风速具有良好的一致性，两者差异的均值为0.2 m·s—1、标准差为1.55 m·s—1。CYGNSS 与浮标或ECMWF 风速相比，均呈现负偏差特性，这主要是因为CYGNSS 反演的高风速明显小于真实值。此外，CYGNSS 相对于浮标或ECMWF 的风速标准差均不超过2 m·s—1，满足海面风场遥感常见的指标要求。总体而言，风速小于10 m·s—1时，CYGNSS 与浮标和ECMWF 风速均具有良好的一致性，且更接近后者。在图6 的基础上，进一步利用2.2 节的三配对分析方法估计CYGNSS 和其他两种参考风速固有的随机误差。不同数据的空间分辨率和时间分辨率可能不一致，即不同数据所测风速精度存在略微差异，为了方便，这里不考虑三种数据源之间的尺度差异，假设其所测得风速精度是一致的。因此式（6）得到的固有误差实际上是在ECMWF 尺度下的风速随机误差[22]。针对3.2 和3.3 节发现的不同卫星之间的风速具有明显的差异性，将三配对数据集分成两组，即第4，7，8 颗卫星（第一组）和第1，2，3，5，6 颗卫星（第二组）两组，分别进行分析，结果列于表1～3。总体而言：以浮标风速为参考，CYGNSS 反演风速的校正系数为1.28（比例因子）和—0.51（偏差系数）；在ECMWF 风速所表征的空间尺度下，ECMWF 风速的固有误差最小（1.00 m·s—1），浮标次之（1.06 m·s—1），CYGNSS 再次之（1.79 m·s—1）。对于第一组数据，CYGNSS 反演风速的校正系数为1.18 和—0.46。在ECMWF 风速表征的空间尺度下，ECMWF 风速的固有误差最小（0.99 m·s—1），浮标次之（1.06 m·s—1），CYGNSS 再 次 之（1.78 m·s—1）；对 于 第 二 组 数 据，CYGNSS 反演风速的校正系数为1.35 和—0.51。在ECMWF 风速表征的空间尺度下，ECMWF 风速的固有误差最小（1.01 m·s—1），浮标次之（1.06 m·s—1），CYGNSS 再次之（1.80 m·s—1）。由此可知：从校正系数角度分析，第一组CYGNSS 反演风速的校正系数为1.18 和—0.46；第二组CYGNSS 反演风速的校正系数为1.35 和—0.51。因此，推断第4，7，8 颗卫星的风速质量略优于其他卫星。另外，以浮标为参考，第一组数据中CYGNSS 的风速固有误差（1.78 m·s—1）也略小于第二组数据的结果（1.80 m·s—1）。

表1 浮标、CYGNSS 和ECMWF 风速的校正系数与固有误差Table 1 Correction factors and inherent errors of buoy, CYGNSS and ECMWF wind speeds

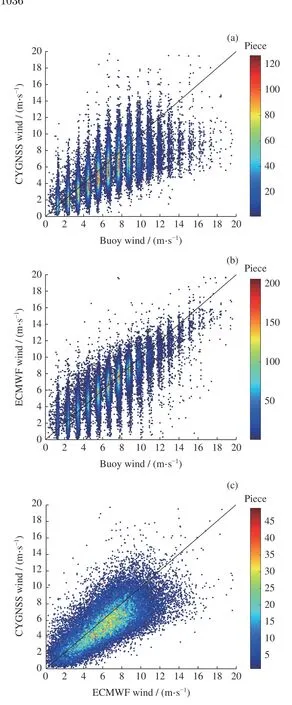
图6 CYGNSS、浮标以及ECMWF 风速两两对比的散点密度Fig. 6 Scatter density plots of CYGNSS versus buoy wind speed (a), ECMWF versus buoy wind speed (b),and CYGNSS versus ECMWF wind speed (c)

3 结论

对CYGNSS 反演风速的时空分布特征进行了详细的分析，发现CYGNSS 风速的时空变异性明显小于ECMWF 的预报风速。与后者相比，CYGNSS 风速的偏差和标准差呈现明显的随时间或空间变化的特性，即高风速区的偏差较大、低风速区的偏差较小，夏冬两季的标准差较大、春秋两季的标准差较小。考虑到GNSS-R 技术对高风速的敏感性较弱，上述差异主要是由不同时间、不同地点海面风速的大小决定的。对CYGNSS 8 颗卫星的风速分别进行分析，发现第4，7，8 颗卫星反演风速的性能明显与其他卫星不同。因此，利用三配对分析方法对匹配的CYGNSS、浮标和ECMWF 数据集进一步分析，以阐明不同数据源风速的固有随机误差。结果表明，在ECMWF 表征的空间尺度下，ECMWF 风速误差最小，其次是浮标风速和CYGNSS 反演风速。总体而言，CYGNSS 风速的固有误差约为1.79 m·s—1。研究结果一方面提供了误差量化结果，为CYGNSS风速数据的业务应用提供参考；另一方面指出了第4，7，8 颗卫星的风速质量略优于其他颗卫星的风速质量。这为进一步标定CYGNSS 的反射测量信号提供依据。

表2 第一组数据浮标、CYGNSS 和ECMWF 风速的校正系数与固有误差Table 2 Correction factors and inherent errors for the first group data set

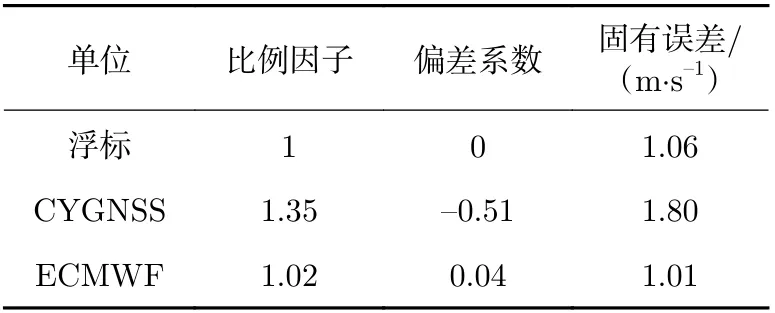
表3 第二组数据浮标、CYGNSS 和ECMWF 风速的校正系数与固有误差Table 3 Correction factors and inherent errors for the second group data set