RBF 神经网络在静电悬浮位置控制中的应用*

陆潇晓 刘晓珂 李 虎 郑 福 孙志斌 于 强

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学计算机科学与技术学院 北京 100049)

0 引言

静电悬浮是一种研究新型材料的无容器悬浮技术，在测量难熔材料热物性、分析材料凝固机理、探索新型材料等方面有着广泛应用[1]。静电悬浮技术通过给电极接通高压，使表面带电的样品克服重力，悬浮在电极之间的电场中，避免了容器壁对材料的接触和污染。相比声悬浮、气悬浮、电磁悬浮等其他悬浮方式，静电悬浮有着扰动小、材料适用范围广、加热控制与悬浮控制相互独立等优势，易于使样品获得更深的过冷程度[2]。

国际空间站[3]和中国的空间站[4]上都配备了静电悬浮实验装置，2021 年发射的中国空间站将在空间开展众多样品的静电悬浮实验。但在空间开展静电悬浮实验的成本极为高昂，实验机会极其稀少，难以满足大量的材料科学实验需求。为配合完成空间静电悬浮实验，需开展大量地基验证实验，提供坚实的技术支持。

1993 年Rhim 等[5]在美国研制了第一台地基静电悬浮无容器设备，随后日本[6]、德国[7]、韩国[8]也先后研制了静电悬浮装置并开展材料深过冷实验。目前，中国的西北工业大学[9]、中国科学院国家空间科学中心[10]和中国科学院空间应用工程与技术中心[11]也开展了静电悬浮技术的研究工作。

样品的位置控制是静电悬浮实验的基础，后续实验操作是在样品稳定悬浮基础上完成的。静电悬浮位置控制系统通过控制高压源的输出电压来改变样品受到的电场力，抵消重力场的作用力，从而控制样品的悬浮位置。因此，样品的表面电荷量直接影响其悬浮状态。在实验过程中，当使用加热激光器对样品进行加热操作时，样品的体积、表面带电量等性质会发生变化，并且静电悬浮位置控制系统自身有着非线性的特点，传统PID（Proportion Integration Differentiation）算法对于系统受到的扰动不能很好地抑制，难以自适应获得稳定的控制效果。尤其是当材料加热过程中因表面状态变化而使表面电荷量骤减，或者热电效应导致表面电荷量骤变时，不及时调整控制参数易造成实验的失败。Nakamura 等[12]使用高速CCD（Charge Coupled Device）代替PSD（Position Sensitive Detector）传感器，研制了以高速CCD 作为样品位置探测器的静电悬浮位置控制系统，减小了位置传感器非线性部分的影响。但是高速CCD 比PSD 传感器成本高且图像采集、传输及处理过程需要极大的计算量，限制了控制周期进一步的调整。Meister 等[13]采用局部线性化和极点配置的方法，设计了一种基于插值的静电悬浮增益调度控制器，但其仅以估计的样品带电量作为调度变量，忽略了样品体积、质量、激光强度等因素的影响。同时，对于不同样品，通过插值进行增益调度的方法在实际工程中存在一定难度。

神经网络技术的兴起为控制技术提供了新的方法和途径。在各种神经网络中，RBF（Radial Basis Function）神经网络是一种性能良好的三层前馈神经网络，具有较好的全局逼近性质，能够逼近任意的非线性函数，并有较快的学习收敛速度[14]。在进行控制器设计时，RBF 神经网络不需要知道系统的精确模型，即可实时对模型参数和扰动进行估计补偿[15]，因此在航天工程[16]、伺服系统[17]、控制领域[18]、环境科学[19]等领域有着广泛应用。

针对静电悬浮位置控制系统非线性和时变性的特点，为提高其自适应性和鲁棒性，本文推导了静电悬浮位置控制系统的机理模型，提出RBF-PID 自适应控制方法，对静电悬浮实验中样品的位置控制进行研究，并通过仿真与实验验证该方法的控制稳定性和抗干扰能力。

1 静电悬浮位置控制系统及建模

1.1 静电悬浮位置控制系统构成

图1 给出了静电悬浮位置控制系统工作原理。静电悬浮位置控制系统中垂直方向的悬浮电极由上电极和下电极组成，上电极与高压源的输出端连接，下电极接地，在上下电极之间形成向上的电场，使带正电的样品受到向上的电场力与重力平衡，实现悬浮。位置控制系统使用PSD 位置传感器作为检测装置，PSD 传感器型号为DL100-7 PCBA3，分辨率为1 μm，测量噪声为15 nV·Hz–1/2。平行光源发出波长632.8 nm、直径2 cm 的光斑，覆盖整个上下电极之间的空间。PSD 传感器位于平行光源的正对面，接收平行光束，并根据样品的阴影位置输出相应的电压信号，电压信号经放大电路和采集电路处理后被控制器读取。

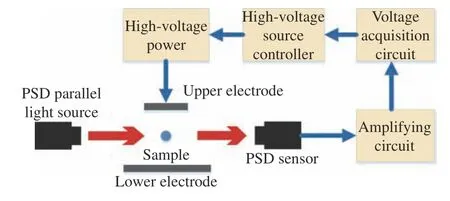
图1 静电悬浮位置控制系统工作原理Fig. 1 Position control system of electrostatic levitation

静电悬浮位置控制系统主要包括位置测量（PSD 传感器）单元、数字控制器（包含位置信号采集电路和放大电路）、执行器输出（高压源）和被控对象（材料样品位置）4 部分，样品的位置控制回路如图2所示。

图2 样品位置控制回路Fig. 2 Control loop of sample position

控制系统通过PSD 传感器获取样品的位置，并与系统设定值进行比较，将二者之差输入给数字控制器，数字控制器通过偏差改变输出的控制信号，使高压源输出的高压相应地变化，达到控制样品位置的目的。

1.2 静电悬浮位置控制系统机理模型

实验的环境为真空环境（真空度为10–5Pa）。在悬浮过程中，样品在垂直方向上受到4 个力的作用：重力、库仑力、上电极镜像力和下电极镜像力。其中，库仑力和上下电极镜像力的合力用以抵消重力，实现样品的悬浮。

假设样品的表面形状是规则的球形，上电极接高压源负极，下电极接地。这里将样品视为位于样品重心处重量为m、带电量为qs的质点。在悬浮的开始阶段，样品放置于下电极上。因为上电极连接了负高压U，负电荷会在上电极表面逐渐累积，相应地，正电荷会在下电极和样品表面逐渐累积。假设上下电极是无穷大的平面，则上下电极之间会形成一个方向向上的匀强电场，样品在电场中受到的库仑力

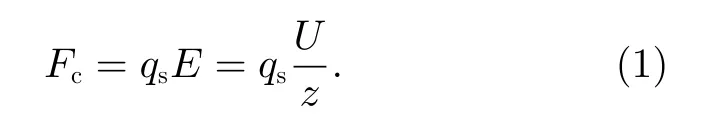
其中,Fc为样品受到的库仑力，qs为样品的表面电荷量，z为上下电极的间距，U为高压源的输出电压。

此外，样品还受到上下极板对样品的镜像力作用。镜像力是一种电荷感应力，当接地平面无限大导体外(距离为r)放置一个正电荷(+q)时，则该电荷将在导体表面上感应出负电荷( -q)，这两个正负电荷之间相互吸引，该吸引力可以采用镜像电荷计算[20]。样品受到上电极的镜像力为其中，ε0为真空介电常数，d为样品距离下电极的高度，qs为样品的表面电荷量，z为上下电极的间距。

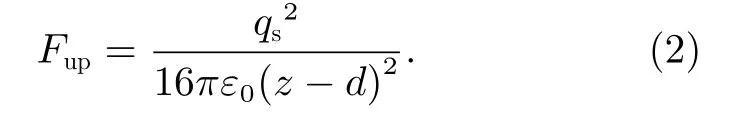
样品受到下电极的镜像力为

假设上下电极间距10 mm，样品质量为70 mg，带电量为10–9C，根据式（4）计算样品稳定悬浮时，样品位置与所施加电压的关系，结果如图3 所示。由图3 可以看出，样品在靠近上电极和下电极的位置时，所需悬浮电压会急剧变化。

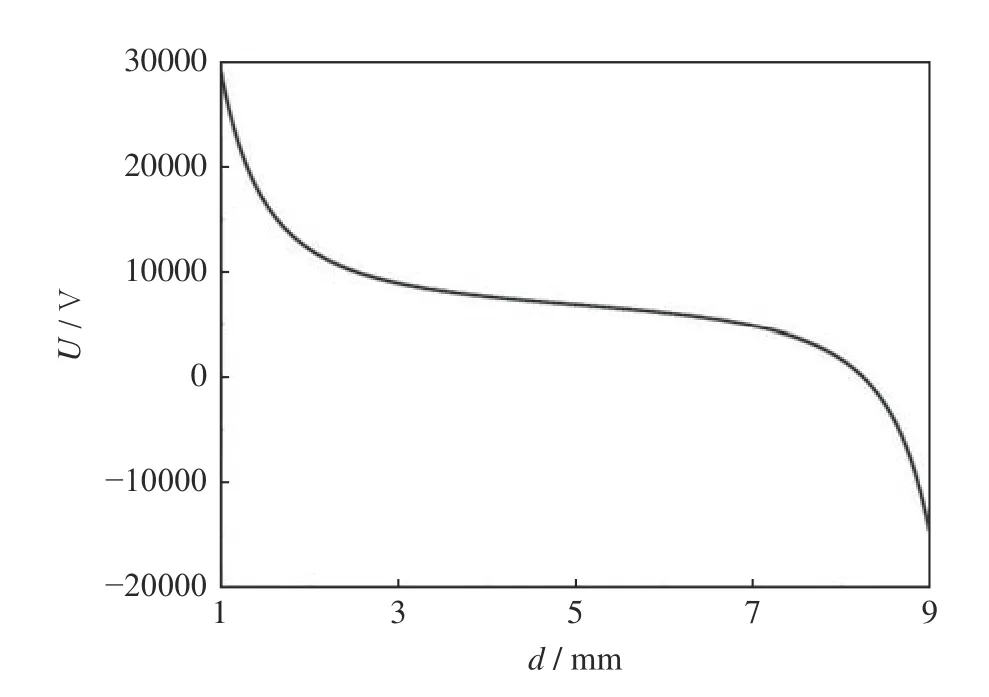
图3 位置平衡处样品位置与控制电压的关系Fig. 3 Relationship between the sample position and the controlling voltage when sample position is in equilibrium

假设样品在起跳后所带电荷量qs保持不变，且最后稳定悬浮于上下电极的正中间，对式（4）进行线性化，可得在平衡位置附近静电悬浮位置系统的传递函数

由此可见，从控制角度来看，在静电悬浮位置控制系统平衡点附近，从高压源电压输入到样品位置输出的传递函数结构是近似二阶的。但是样品偏离平衡状态的程度较大时，该传递函数与实际实验模型会存在偏差。

2 RBF-PID 自适应控制

2.1 RBF 神经网络

RBF 神经网络具有很强的非线性拟合能力，在实时辨识系统方面有着许多应用[21,22]。典型的RBF 网络是一个三层前馈网络，包含输入层、隐含层和输出层，如图4 所示。

图4 RBF 神经网络结构Fig. 4 Structure diagram of RBF neural network

其中,cj为第j个神经元高斯基函数的中心矢量，σj为第j个神经元高斯基函数的宽度。RBF 网络隐含层到输出层之间为线性映射，转换函数为

其中，ωj为第j个神经元的输出权重。

2.2 RBF-PID 控制器的设计

考虑到在实验过程中，样品的体积、重量、带电荷量等因素变化都会导致位置控制系统状态的变化，且这些变化是随机的、无重复性、无特征性。在这种情况下，为了增强模型在多种状态下的适用性以及位置控制系统的鲁棒性，使用RBF-PID 控制方法调节RBF 神经网络的结构与权值，并根据模型预估值与目标值之差调整PID 控制参数。基于RBF-PID 控制器的总体控制回路如图5 所示。

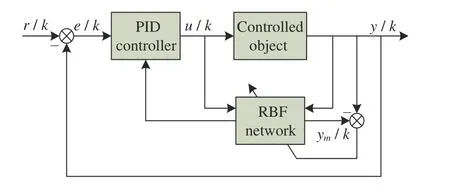
图5 RBF-PID 控制器结构回路Fig. 5 Structure loop diagram of RBF-PID controller

首先，手动设置kp，ki，kd参数的初值，以及RBF神经网络的隐含层节点数、学习速率和动量因子。RBF-PID 控制器根据系统的输入与输出，使用梯度下降法[24]调整内部神经网络的节点中心矢量、基宽度和输出权值，实时快速辨识系统的状态，有

其中，η为学习效率，α为动量因子，ωj为神经元节点的输出权值，σj为神经元节点的基宽度，cji为神经元节点的中心矢量。式(8)～(11)为迭代更新。

在获得模型状态的情况下，RBF-PID 控制器根据网络预测值与给定目标值之间的差值，修改PID 三个控制参数，达到自适应控制的效果，有

式(12)～(15)为PID 控制参数迭代调节方法。

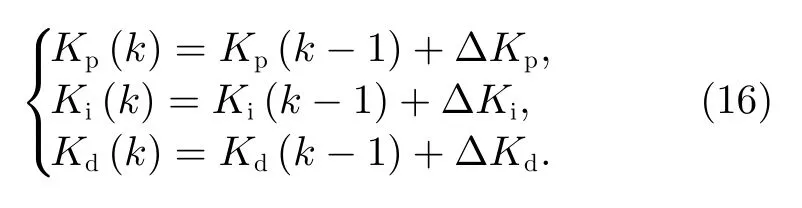
最后，更新PID 参数，并使用更新后的PID 参数对系统进行控制，有图6 为静电悬浮位置控制系统的非线性仿真结果，RBF-PID 模块包含PID 控制器和RBF 神经网络，系统模型模块包含输入电压、样品的受力和运动情况。在RBF-PID 控制器中，RBF 网络辨识模块的输入参数有三个，即当前时刻样品的位置、速度与控制高压。根据经验，设RBF 隐含层结点个数为250，基函数半径σ为0.12，学习速率η为30，动量因子α为0.04，初始PID 参数P=10000，I=120，D=20000，PID 学习速率分别为ηp=500，ηi=850，ηd=350。系统仿真参数列于表1。通过样品更新后的数据调整RBF 网络节点的中心位置和宽度，计算出更新的

表1 系统仿真参数Table 1 Parameters of system simulation

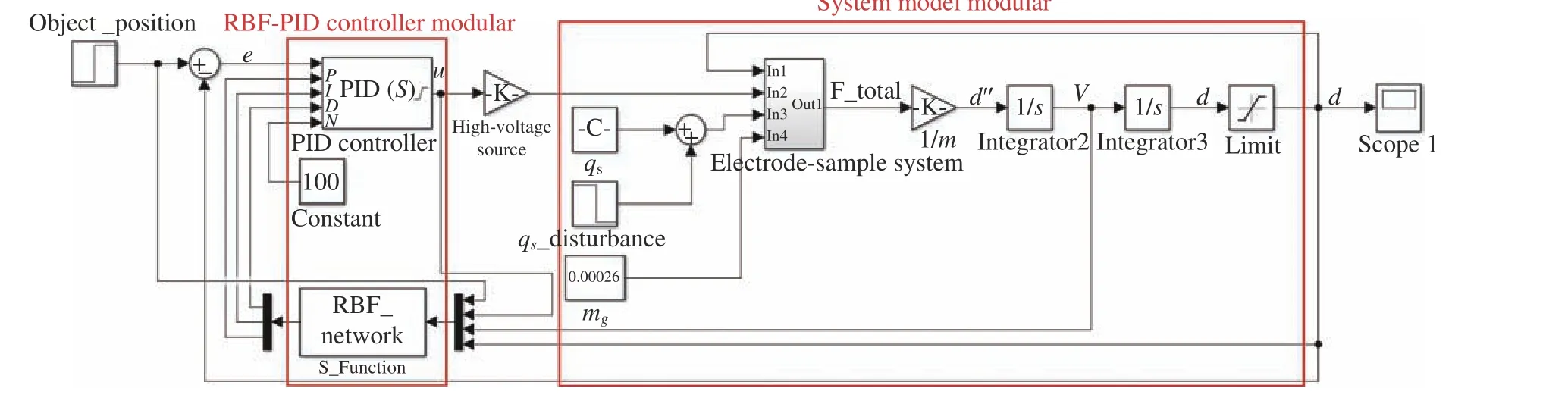
图6 静电悬浮位置控制系统非线性仿真结果Fig. 6 Nonlinear simulation result of position control system of electrostatic levitation

3 仿真与实验

3.1 仿真分析

PID 参数，并更新电压与样品位置，以此类推。

为验证RBF-PID 控制器的鲁棒性，将传统PID控制器与二次型目标函数最优整定后的PID 控制器对比，仿真结果如图7 和图8 所示。

图7 为样品在起跳悬浮阶段时三种控制方法的初始响应曲线。从图7 中可以看出，传统PID 控制器的控制效果并不理想，虽然最后样品可以悬浮至设定位置，但是在悬浮上升阶段系统有着大幅振荡，且上升时间较长。二次最优整定PID 控制器的I 参数初始值较大，比RBF-PID 控制器早0.008 s 起跳。在悬浮上升阶段，两种控制器的响应曲线都很平滑，没有振荡现象。在接近设定目标值时，RBF-PID 控制器无超调发生，而最优整定PID 控制器有0.5 mm的超调。从开始起跳到稳定悬浮，最优整定的PID 控制器耗时约0.1 s，RBF-PID 控制器耗时约0.065 s。因此，RBF-PID 控制器的上升时间更短，超调更小，到达稳定所需时间更少。

图7 各控制器的初始响应曲线Fig. 7 Initial response curve of different controllers

图8 为样品的表面电荷量突变为原来的0.5 倍、2 倍和3 倍时，传统PID 控制器、最优整定的PID 和RBF-PID 三种控制器对抗扰动的响应曲线。

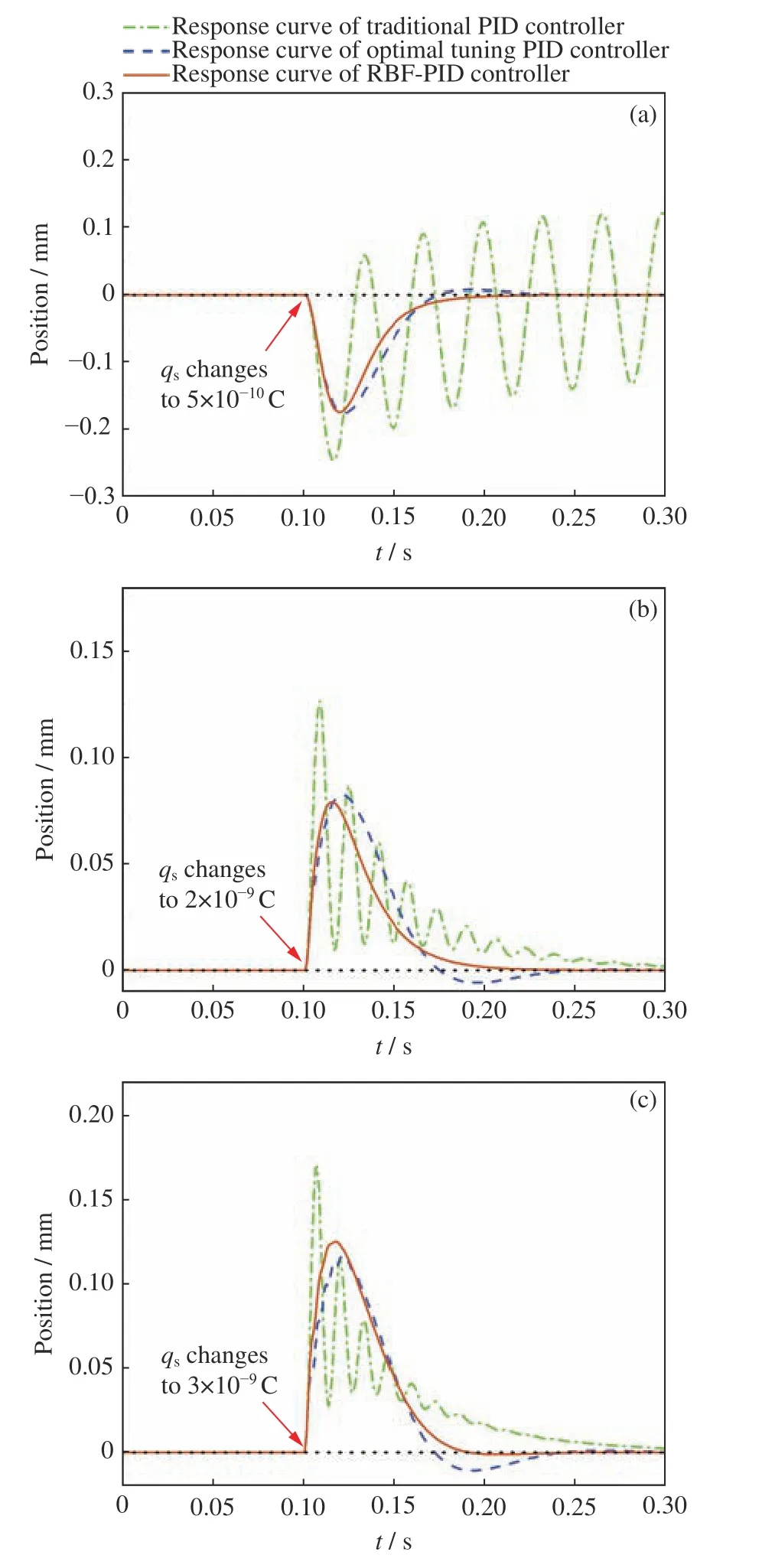
图8 电荷量突变时各控制器的响应曲线Fig. 8 Response curve of different controllers when the charge changes suddenly

从图8 中可以看到，当电荷量突增或骤减时，传统PID 控制方法需要较长时间到达稳定状态，且伴随有高频的振荡。最优整定的PID 控制器在控制的过程中有多次较小的振荡现象出现，且会有超调情况出现； RBF-PID 控制器对应的响应曲线较为平滑，无振荡现象，从扰动出现到样品位置控制稳定需要的时间最少。仿真实验的对比分析列于表2。由此可以认为当样品电荷量突变时，RBF-PID 控制器更稳定、更快速，有着更强的抗干扰性和鲁棒性。

表2 仿真结果对比Table 2 Comparison of simulation results

通过仿真实验可以看出，RBF-PID 控制器与传统PID 控制器和最优整定的PID 控制器相比，在起跳时具有更快的响应速度，悬浮控制过程更加快速平稳、无震荡；在样品表面电荷突变时，RBF 神经网络可以快速辨识系统状态，并实时更新控制参数，使输出依旧能很好地跟踪输入。

3.2 实验验证

为了验证所提出的控制方法在静电悬浮位置控制系统中的有效性，使用直径2 mm 的锆球样品作为控制对象，依据仿真结果对位置控制参数进行实时调整。实验系统的采样和控制频率为300 Hz。图9 为静电悬浮实验装置。样品锆的悬浮实验如图10 所示。实验环境的真空度为10–5Pa。

图9 静电悬浮实验装置Fig. 9 Experimental facility of electrostatic levitation

图10 样品锆悬浮实验Fig. 10 Diagram of sample zirconium in levitation state

图11 为室温下三种控制方法的控制效果对比。从图11 可看出：常温下，传统PID 控制器样品位置误差在–0.13～0.11 mm 之间，平均绝对误差为0.0384 mm；最优整定的PID 控制器样品位置误差在–0.08～0.11 mm 之间，平均绝对误差为0.0269 mm；参数实时调整后样品位置误差在–0.095～0.08 mm 之间，平均绝对误差为0.0172 mm，控制效果比传统PID 方法提高55%。

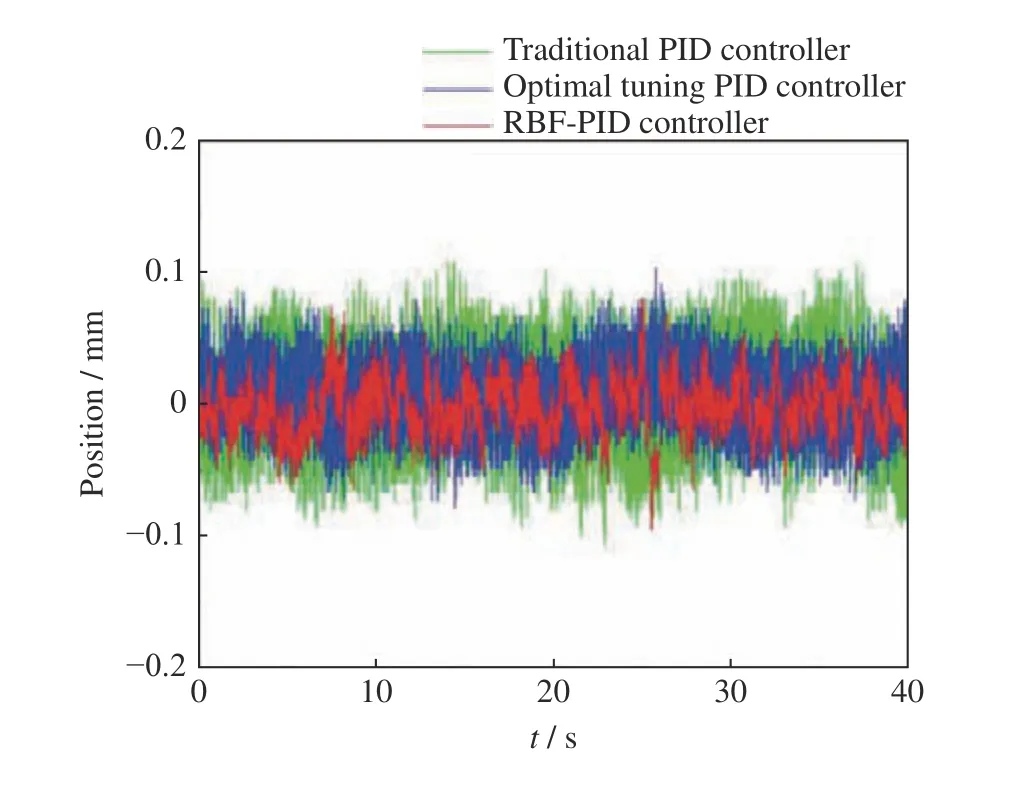
图11 室温下各控制器的样品位置对比Fig. 11 Sample position comparison of different controllers at room temperature

当使用红外激光器给样品加热时，由于体积、表面电荷量等因素的变化，样品会出现大幅振荡现象，尤其是当样品初次处于半融化状态时，样品电荷量突增和骤减的情况发生最频繁，样品位置振荡最剧烈，位置控制系统的干扰量最大。当样品处于初次熔化的过程中，三种控制方法的样品位置误差如图12所示。从图12 可以看出，传统PID 控制器的样品位置误差在–0.43～0.69 mm 之间，平均绝对误差为0.1879 mm；最优整定的PID 控制器样品位置误差在–0.143～0.296 mm 之间，平均绝对误差为0.0685 mm；控制参数实时调整后样品位置误差为–0.14～0.185 mm，平均绝对误差为0.0416 mm，控制效果比传统PID 提高70%。基于RBF 神经网络实时调整控制参数的方法与传统PID 控制器和最优整定的PID 控制器的控制效果对比引于表3。

表3 实验结果对比Table 3 Comparison of experimental results

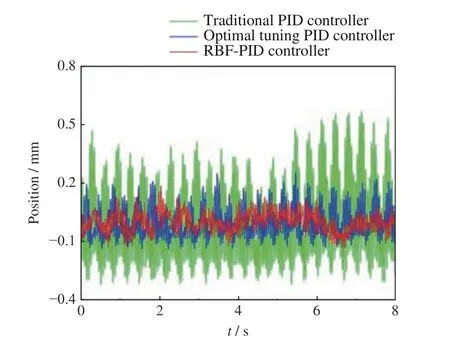
图12 加热状态下各控制器的样品位置对比Fig. 12 Sample position comparison of different controllers at heating state

4 结论

根据静电悬浮位置控制系统及其理论模型，提出了一种基于RBF 神经网络的静电悬浮位置系统的控制方法。该方法利用RBF 神经网络，通过系统的输入与输出量，实时辨识系统状态，并根据网络模型更新PID 控制参数，实现静电悬浮位置系统的自适应控制。仿真结果表明：当样品带电量从10–9C 突变至3×10–9C 时，RBF-PID 控制器只需0.1 s可使系统达到稳定状态。依据仿真结果对控制参数进行实时在线调整，实验结果表明：室温条件下，参数实时调整后系统的平均绝对误差为0.0172 mm，比PID 控制效果提高55%；加热状态下，参数实时调整后系统的平均绝对误差为0.0416 mm，比PID 控制效果提高70%。所提的控制方法对系统有较高的辨识精度，当系统存在较大扰动时可以快速抑制干扰，使输出良好地跟踪输入，具有比传统PID 控制方法更高的稳定性、鲁棒性和抗干扰性。