Volta’s混沌系统的控制与同步

王东晓，李自强

(郑州航空工业管理学院 数学学院,河南 郑州 450046)

1 引 言

混沌是非线性系统普遍存在的现象，混沌理论所研究的是非线性动力学混沌，目的是要揭示貌似随机的现象背后可能隐藏的简单规律，以求发现一大类复杂问题普遍遵循的共同规律。混沌系统同步属于混沌控制范畴，有着广泛的应用前景，同步问题备受关注，新的系统及新的研究方法层出不穷。

毛北行等[1-4]研究了非线性复杂网络混沌系统的有限时间同步问题，并对滑模同步两种方法进行比较，发现分数阶相比整数阶系统存在更普遍。张燕兰等[5-6]采用自适应方法实现分数阶Rayleigh-Duffling-like系统的广义投影同步；余明哲等[7]滑模自适应同步了一类不确定分数阶系统；钟启龙等[8]采用主动滑模研究了分数阶混沌系统同步问题；Tino等[9]发现两个不同系统的同步也可以利用自适应滑模控制来实现；Volta’s混沌系统在物理、通讯等方面有着广泛的应用[10-11]；张振等[12]研究了分数阶Volta’s系统同步问题；李娇[13]研究了Volta’s系统的混合投影同步；张志明等[14]对Volta’s混沌系统添加一个新的状态变量，得到一个四维的自治超混沌系统。在上述研究的基础上,本文研究了Volta's混沌系统的控制与同步问题，得到一个新的五维系统，并给出了系统实现同步的两种方案，最后通过数值仿真结果表明方案的有效性和可行性。

2 五维系统

如下的三阶Volta's混沌系统[10-11]

(1)

系统初始值(x1(0),x2(0),x3(0))=(1，2，8)，此时系统呈现混沌态，如图1所示。

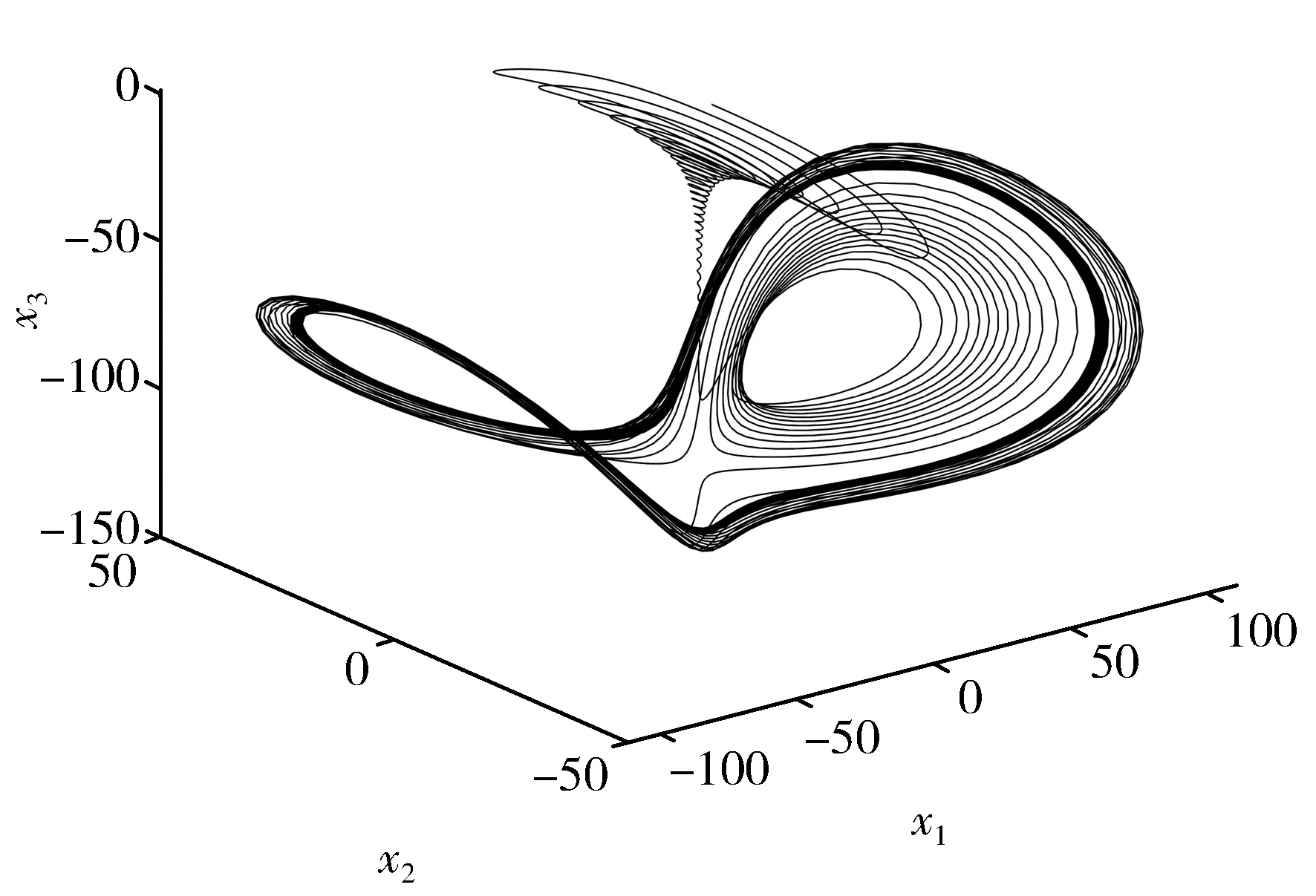
图1 系统(1)的混沌吸引子

文献[14]在系统(1)中添加一个变量x4，得到一个四维自治的超混沌系统

(2)

系统初始值(x1(0),x2(0),x3(0),x4(0))=(8,2,1,1)，此时系统呈现混沌态，如图2所示。

图2 系统(2)的混沌吸引子

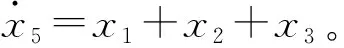
(3)

系统初始值(x1(0),x2(0),x3(0),x4(0),x5(0))=(85,-50,-90,-40,-30)，此时系统(3)的相图如图4所示。

(a) x1-x2-x3

3 线性同步

以系统(3)作为驱动系统，参数r=30,其对应的响应系统设计为:

(4)

其中ui为控制器,取误差变量ei=yi-xi,(i=1,2,3,4,5)，误差系统如下：

(5)

定理1构造控制方案，选取控制器：

U1=k1e1;U2=k2e2;U3=k3e3;U4=k4e4;U5=k5e5，在该方案控制下，误差系统(5)趋于零，主从系统(3)与(4)同步。

证明:构造Lyapunov函数

则Lyapunov函数关于时间t的导数：

=e1[-e1-5e2-(e2e3+x2e3+e2x3)-10e4-u1]+e2[-85e1-e2-(e1e3+e1x3+x1e3)-30e5-u2]+2e3[(e1e2+e1x2+x1e2)+e3-2u3]+e4[e1-u4]+e5[e1+e2+e3-u5]

由混沌系统的有界性，存在M>0，满足max{|90+2x3|,|x2|,|x1|}≤M

=-eAeT

其中e=(|e1|,|e2|,|e3|,|e4|,|e5|)，

4 滑模同步

在实际应用中，系统中往往掺杂着一些不确定项或是扰动项，我们考虑在此种情况下的系统同步问题。

以系统(3)作为驱动系统r=30,其对应的响应系统设计为:

(6)

其中Δfi(y)为不确定项，di(t)为外部扰动，ui为控制器,取误差变量ei=yi-xi(i=1,2,3,4,5)，误差系统如下：

(7)

假设1参数mi,ni>0，使得|Δfi(y)|

定理2构造控制方案，选取控制器：

在该方案控制下，误差系统趋于零，主从系统(3)与(6)同步。

证明：当状态变量在滑模面上运动时，s=0，将控制输入ui(t)代入误差系统(7)，其第一个方程即为：

当系统状态变量不在滑模面上运动时，构造Lyapunov函数

则Lyapunov函数关于时间t的导数：

控制器代入

=s[-e1-e2-e3-e4-e5]=-s2

5 数值仿真

图6 定理2的系统误差曲线

6 结 论

本文研究了Volta's混沌系统，添加状态变量得到新的系统，并实现它的同步控制问题。分别采用线性控制和滑模控制法设计了控制方案,得到了Volta's混沌系统同步的充分性条件,并给出了严格的数学证明和推理过程,最后通过数值仿真表明该方法的有效性和可行性。