带有外部输入项的时间周期SIR 传染病模型的周期行波解*

宋 雪，杨赟瑞，杨 璐

（兰州交通大学 数理学院，兰州 730070）

引言

反应扩散方程的行波解在生态学、传染病学、种群动力学、生物化学等领域有着广泛的应用[1-3]，例如，传染病的传播、种群的入侵等.目前，关于经典Laplace 扩散方程行波解的研究[4-6]已相对成熟，特别是SIR 传染病模型一直是重点研究对象[4-5].例如，Wang 等[4]分別利用Schauder 不动点定理和双边Laplace 变换研究了SIR 传染病模型

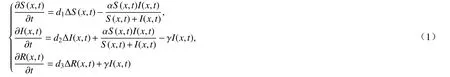
行波解的存在性和不存在性，其中S,I,R分别表示易感者、感染者和治愈者的密度，di＞0(i=1,2,3)表示扩散率，α表示感染率，γ表示恢复(或治愈)率.此后，Wang 等[5]在模型(1)的基础上，研究了总人口数不变的SIR 传染病模型行波解的存在性和不存在性.

现实生活中，人口的增长和传染病的传播会受到时间周期因素的影响.例如，麻疹、风疹和腮腺炎等传染病会随季节的变化呈现周期性爆发.因此，研究具有时间周期反应扩散方程的行波解更符合客观现实[7-9].2018 年，Wang 等[7]研究了相应于模型(1)的具有时间周期的SIR 传染病模型：

2017年上半年，广东海事局积极策划“平安西江”建设启动仪式方案。8月8日的启动仪式上，在广东海事局的倡议下，沿江六地市政府、省直6个部门、广东海事局共13个共建方共同签署了《“平安西江”共建协议书》，构建“水上安全命运共同体”，形成了“共商、共建、共享”的局面，为打造“安全、畅通、绿色、高效”的西江航运大通道提供安全保障。

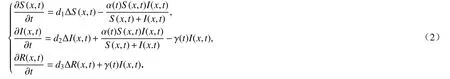
利用Schauder 不动点定理和渐近传播速度的性质建立了模型(2)周期行波解的存在性和不存在性.此后，Wu 等[8]将模型(2)的结果推广到具有一般非线性发生率的时间周期 SIR 传染病模型：

关于具有时间周期反应扩散方程的行波解研究，还可参见文献[10-13]等.

建立模型(5)周期行波解的存在性时，由于模型(5)不具有单调性，常用的单调性方法如比较原理、单调迭代技术[17]、单调半流理论[18]等失效.而通过构造适当的上下解并结合 Schauder 不动点定理对非单调方程完全适用.为此，首先通过构造适当的上下解定义闭凸锥，利用 Schauder 不动点定理证明了模型(5)周期行波解的存在性.其次，借助分析技术证明了模型(5)周期行波解的不存在性.注意到，模型(5)将不含时滞的模型(4)行波解的研究推广到了周期情形.另外，当时，模型(5)退化为模型(2).因此，本文完善了不考虑外部输入和自然死亡的传染病系统周期行波解的研究结果[7-8]，并将SIR传染病系统行波解的研究[16]推广到了时间周期的 SIR 传染病系统的周期行波解.

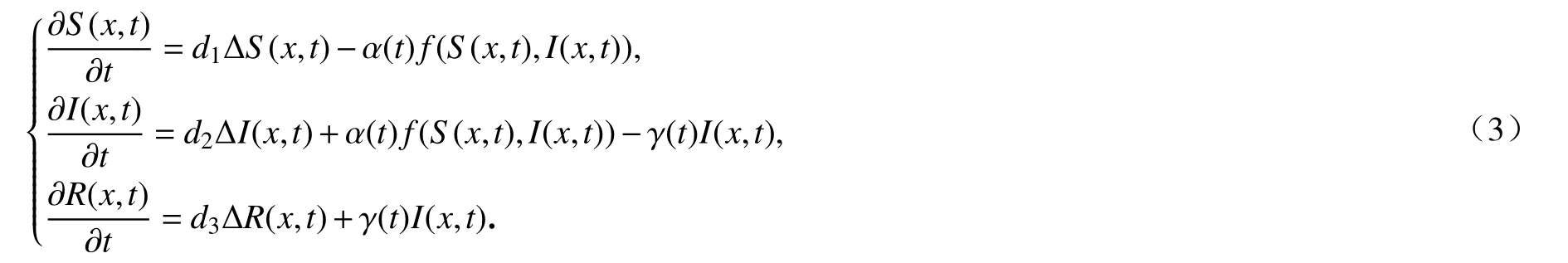
高效解法：∵∠CMP=∠OHP=90°, ∴∠CPM=90°-∠CPO=∠POH，又CP=OP，∴△PCM ≌△OPH， OH=2PH=（2√ 5/5）PO，S△ OPM =OH²/2=4/5 。

(A1)当S,I≥0时，f(S,I)是二阶连续可微的；当S,I＞0时，f(0,I)=f(S,0)=0.

第三种情况涉及三个行为，即窃取他人信用卡信息资料的行为，伪造信用卡的行为，使用伪造信用卡实施转账、套现、取现的行为。行为人前后所实施的三个行为都是基于同一犯罪故意，即掩饰、隐瞒诈骗犯罪所得及其产生收益的故意，形成两个层次的牵连犯，即窃取他人信用卡信息资料的手段行为和伪造信用卡的目的行为的牵连，伪造信用卡作为手段行为与隐瞒犯罪所得及其收益的目的行为的牵连。由于行为人是基于同一目的，三个行为之间有着主观和客观上的密切联系，因此先按照牵连犯的处断原则分析前两个行为的牵连关系，再将确定罪名与掩饰、隐瞒犯罪所得、犯罪所得收益罪视为牵连犯，最后按照牵连犯的处断原则确定一个罪名。

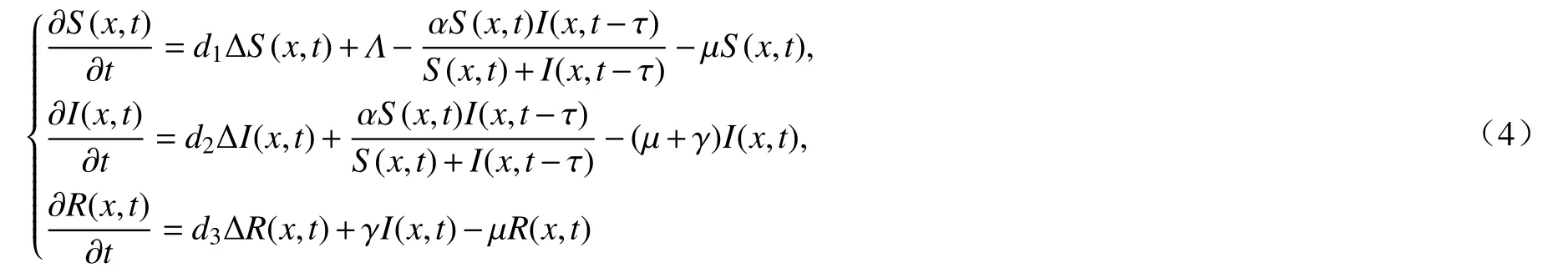
其中ε ＞0是一个正常数.然后通过构造辅助系统(9)适当的上下解并结合Schauder 不动点定理建立辅助系统(9)周期解(ϕε(z,t),ψε(z,t))的存在性.最后，令ε →0,证明(ϕε(z,t),ψε(z,t))的极限函数(ϕ(z,t),ψ(z,t))的存在性，即系统(7)周期解的存在性.

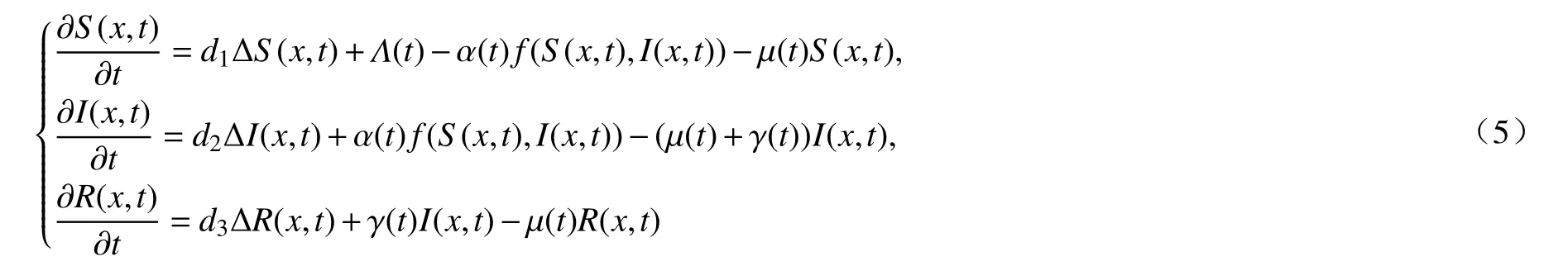
1.4 统计学方法 采用SPSS 19.0统计软件处理。计量资料以表示,均数间比较采用t检验，计数资料组间比较采用χ2检验，以P<0.05为差异有统计学意义。

(A2)当S＞0,I≥0时，∂2f(S,I)＞0,∂22f(S,I)≤0；当S≥0,I＞0时，∂1f(S,I)有界且为正的.

莱茵哈德·根策尔成长于德国黑森林里的小城市弗莱堡。年轻的时候，他是德国最好的标枪运动员之一，甚至能与国家队一起备战1972年慕尼黑奥运会。现在，他的“标枪”掷向了更远的地方。

1 预备知识

行波解的存在性和不存在性，其中，Λ表示外部输入率，µ表示自然死亡率.注意到，模型(4)并没有考虑时间周期因素的影响，基于此，本文研究了带有外部输入和自然死亡的时间周期 SIR 传染病模型周期行波解的存在性和不存在性，其中Λ,α,γ,µ是关于t的严格正T周期连续函数，非线性发生率f(S,I)满足如下条件：

然而，上述模型并没有考虑外部输入和自然死亡的影响，对病程较长的传染病，外部输入和自然死亡是不可忽略的因素.因此，考虑外部输入和自然死亡的 SIR 传染病模型的行波解研究，引起了学者们的广泛关注[14-16].例如，Zhou 等[16]分别利用 Schauder 不动点定理结合 Lyapunov 函数方法、双边 Laplace 变换，研究了带有外部输入和自然死亡的 SIR 传染病模型

2 周期行波解的存在性

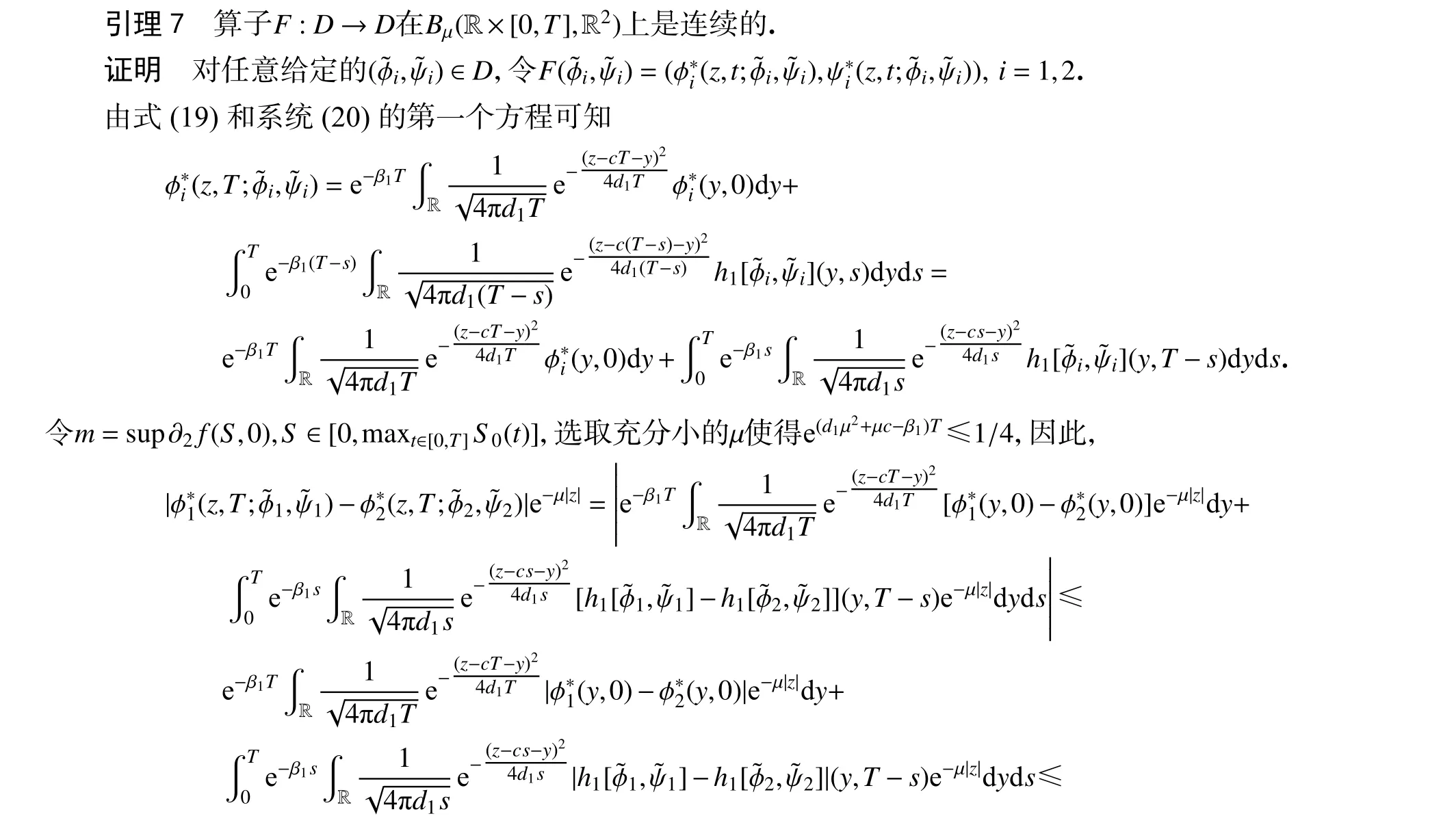
本节中，首先构造辅助系统(9)的上下解并定义闭凸锥，将系统(5)周期行波解的存在性转化为定义在这个闭凸锥上的非单调算子存在不动点的问题，并借助Schauder 不动点定理证明了当ℜ0＞1,c＞c*时，辅助系统(9)周期解的存在性.其次，利用Ascoli-Arzela 定理证明了行波系统(7)周期解的存在性，即系统(5)周期行波解的存在性.

2.1 上下解构造

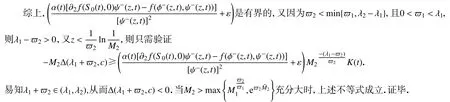
2.2 不动点问题

3 周期行波解的不存在性

4 应用举例

5 结论

本文研究了一类带有外部输入项的时间周期SIR 传染病模型周期行波解的存在性和不存在性.首先，通过构造适当的上下解定义闭凸锥，结合Schauder 不动点定理建立了时系统(5)周期行波解的存在性.接下来，借助分析技术证明了时系统(5)周期行波解的不存在性.注意到，由于系统(5)中的扩散项是Laplace 扩散，它主要适用于小范围的传染病扩散.因此，系统(5)对应的非局部扩散系统周期行波解的存在性和不存在性是今后可以继续研究的问题.