耦合敏感参数实时识别的新型数据同化算法研究——以湖泊藻类模拟为例*

张 帅，彭福利，季雨来，张 京，张奇谋，李 琪，钱 瑞，齐凌艳，黄佳聪**

(1：安徽师范大学地理与旅游学院，芜湖 241003) (2：中国科学院南京地理与湖泊研究所, 中国科学院流域地理学重点实验室，南京 210008) (3：中国环境监测总站，北京 100012) (4：资源环境与地理信息工程安徽省工程技术研究中心，芜湖 241003)

湖库富营养化与藻类水华是我国面临的突出水环境问题，2020年《中国环境状况公报》数据显示，在我国110个重点监测的湖库中有29%处于富营养化状态，其中三湖(太湖、滇池、巢湖)全部处于富营养化状态[1]，造成蓝藻水华频发[2]；2018年夏季，巢湖湖心区和西北岸暴发了面积约121.38 km2的蓝藻水华，严重影响周边居民日常生活和用水安全[3]. 提前预测藻类未来变化，并采取应急措施能够有效缓解蓝藻水华造成的危害[4]；近年来，我国在巢湖等210个重点湖库设置了349个监测站，积累了长时间历史系列的人工与自动监测数据，并在此基础上，构建了包含白洋淀[5]、太湖[6]、巢湖[7]等湖泊的藻类动态模型. 但湖泊藻类动态变化过程十分复杂[8]，数值模拟难度大，亟需依托与日俱增的海量监测数据，发展模型-数据融合算法，提升模型模拟精度[9].

数据同化是在模型和观测的误差估计基础上，在模型运行过程中，实时融合观测数据的方法[10]；是融合模型与数据、提升模拟精度的重要技术之一[11]. 最初应用于数值天气预报，为天气预报提供初始场的数据处理技术[12]；目前已广泛应用于大气[13]、海洋[14]等领域，在生态环境领域也有相关应用[15]，包括流域水文模型、湖泊藻类模型等，并取得了良好应用效果[16]. 集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)是数据同化领域主流的算法之一，其通过蒙特卡洛方法计算状态的预报误差协方差，用集合的思想解决了实际应用中背景误差协方差矩阵的估计和预报困难的问题，能够有效降低数据同化计算量，具有程序设计相对简单、可应用于非线性系统、易于实现并行运算等优点[11,17]. 但集合卡尔曼滤波应用于湖泊藻类动态模型中，缺乏模型敏感参数动态变化的现实[18-20]，导致模型模拟精度提升效果有限，还存在可能增加模型不确定性的不足[21]. 参数敏感性分析能够有效识别复杂模型的关键参数，是实时跟踪敏感参数动态变化的有效方法[22]，有望与数据同化耦合，实现对模型敏感参数的靶向更新，精准提升模型模拟精度.

本研究通过集合卡尔曼滤波与参数敏感性分析的耦合，开发了一种能够实时识别敏感参数的新型数据同化算法，为湖泊藻类动态模型模拟精度提升提供技术支持. 新型数据同化算法将参数敏感性分析耦合到集合卡尔曼滤波，在模型运行每一阶段，根据敏感性分析定位敏感参数，采用集合卡尔曼滤波同步同化状态变量和敏感参数. 由此可精确定位并调整每阶段敏感参数，实时校正模型运行轨迹，减少模型模拟不确定性，提升模型模拟精度. 为验证新算法，以巢湖为研究对象，依据水质自动监测数据，将新型数据同化算法应用于湖泊藻类动态模型[23]，检验新算法对模型精度的提升效果，研究成果也为其它湖库水质模型数据同化提供技术参考.

1 材料与方法

1.1 研究区概况

巢湖(31°26′～31°42′N，117°17′～117°51′E)位于安徽省中部、合肥市内，由巢湖、肥东、肥西和庐江一市三县环抱，湖长54.5 km，最大宽度21 km，平均水深3 m，面积约787 km2，容积约20亿m3(图1)，是沿岸居民生活生产的主要水源[24]. 巢湖入湖河流约33条，其中6条主要入湖河流为杭埠河、白石天河、兆河、柘皋河、南淝河和派河；出湖河流主要为裕溪河，连接长江. 近年来随着流域内人口增加，工农业迅速发展，城镇工业废水、生活污水排入，导致水体营养盐增加，蓝藻水华事件频发，水质恶化，影响周围居民饮用水安全[25]. 此外，蓝藻水华还分泌毒素，危害人类健康[26]. 因此，巢湖富营养化已成为突出的生态、环境和社会问题[27].

图1 巢湖与水质自动监测站分布Fig.1 Locations of Lake Chaohu and its automatic water quality monitoring stations

1.2 数据

巢湖水质监测数据来自8个自动监测站的逐日监测(图1)，监测指标包括水温(WT, ℃)、总磷(TP, mg/L)、总氮(TN, mg/L)及叶绿素a浓度(Chl.a, μg/L)等，监测时间为2020年1-5月. 气象数据来自国家气象信息中心(http://data.cma.cn/)的巢湖站(图1)，位于巢湖东部沿岸，代表巢湖气象条件；气象指标包括最低气温(℃)、最高气温(℃)、平均气温(℃)、日照时长(h)、平均风速(m/s)及降水量(mm)等. 以上数据为湖泊藻类动态模型运行与校验数据.

1.3 巢湖藻类动态模型

目前已开发了系列湖泊藻类模拟模型，如澳大利亚西澳大学水研究中心的ELCOM-CAEDYM模型[28]、威廉玛丽大学海洋学院维吉尼亚海洋科学研究所的Environmental Fluid Dynamics Code(EFDC)模型等[29]. 但此类模型多需要海量、高时空分辨率的数据输入，部分数据难以实时获取，不适用于湖泊藻类的短期(1～3 d)模拟预测[30]. 为解决模型复杂数据输入问题，国内外结合研究区特征，开发了少量数据输入的湖泊藻类动态模型[31-32]. 本研究采用黄佳聪等构建的湖泊藻类动态模型[23](图2).

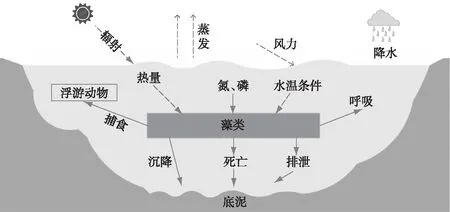
图2 湖泊藻类动态模型概念图[23]Fig.2 Conceptual diagram of phytoplankton dynamic model for lakes[23]

该模型采用叶绿素a浓度表征藻类生物量，藻类动态变化模拟分为两个模块(表1、表2)：①藻类生消模块：用于模拟藻类在太阳辐射、水温、营养盐等条件下的生长，以及在排泄、沉降、呼吸、死亡、被浮游动物捕食等机理过程中的消亡；②基于二维水动力的藻类运移模块：用于模拟藻类在水动力作用下的运移过程. 其它机理过程的数学表达可以参考文献[23]. 为了兼顾模型运行效率与算法耦合效率，本研究仅考虑了点位的藻类模拟，即模型为零维模型，仅考虑藻类生长与消亡等过程导致的藻类动态变化，不考虑水动力输移对藻类的影响. 相比于其它模型，该模型输入数据易实时获取，能满足国内湖泊藻类模拟预测的需求.

表1 湖泊藻类生消过程表达[23]

表2 藻类模型参数与变量[23]

Tab.2 Parameters and variables of the phytoplankton model[23]

类型简称描述单位初值参数Umax藻类最大生长速率d-11.145Topt藻类生长的最佳水温℃27α水及非藻类吸收短波辐射的平均消光系数m-10.45β藻类吸收短波辐射的平均消光系数μg Chl/(L·m)0.016h水深m3.0Iopt饱和光强MJ/(m2·d)12Gsc太阳常数MJ/(m2·d)1367φ纬度(°)31.5KP影响藻类磷吸收的米氏常数μg/L10KN影响藻类氮吸收的米氏常数μg/L22K藻类沉降速率m/d0.0864GRmax浮游动物最大捕食速率d-10.09Fmin可供捕食藻类最小浓度μg/L100Fs可供捕食藻类米氏常数μg/L500km藻类死亡引起叶绿素a减少速率系数d-10.027kr藻类呼吸引起叶绿素a减少速率系数d-10.17ke藻类排泄引起叶绿素a减少速率系数d-10.01ϑ温度因子1.08待解变量T水体温度℃r光衰减系数mChl叶绿素a浓度μg/LI水体表面光强MJ/(m2·d)S日照时数hS0昼长hk离心校正因子U藻类生长速率d-1RA藻类呼吸速率d-1SA藻类沉降速率d-1MA藻类死亡速率d-1GA藻类被捕食速率d-1EA藻类排泄速率d-1δ太阳赤纬°ωs日落时角°DP水体可溶性磷μg/LDN水体可溶性氮μg/LRAmax藻类最大呼吸速率d-1F可供捕食藻类浓度μg/L

1.4 新型数据同化算法

基于集合卡尔曼滤波的数据同化在模型运行的每一阶段会对状态变量和模型参数进行调整[18]. 算法运行分两步骤：预测和更新. 预测：利用模型模拟状态变量先验值集合；更新：根据实测值统计卡尔曼增益并估计状态变量和参数，作为下一时刻的模型输入[33]. 算法递推式运行，每阶段的更新只依赖于上一时刻集合空间，运行效率高[11]，但难以应对模型参数敏感性动态变化的问题.

敏感性分析能够在多参数模型中有效识别关键参数，从而减少敏感参数对模型的影响，使模型模拟更加精确[22]. 本研究决定采用的扰动分析法简单实用且应用普遍[34]，采用此方法对湖泊藻类动态模型的参数进行敏感性分析. 扰动分析法基本思路如下：选定一个参数作为敏感性分析目标，其它参数都保持不变，将目标参数在一定范围内取值扰动n次并计算模型输出，依次求出相邻两次扰动的敏感程度，取平均值作为目标参数的相对敏感度S(式(6))(表3). 该方法简单高效，既方便耦合模型又能兼顾运行效率. 根据本研究湖泊藻类动态模型的机理和结构，将模型的参数敏感程度划分为5个等级：不敏感(Ⅰ，|S|<0.25)；弱敏感(Ⅱ，0.25≤|S|<0.5)；一般敏感(Ⅲ，0.5≤|S|<0.75)；比较敏感(Ⅳ，0.75≤|S|<1.0)；极度敏感(Ⅴ，|S|≥1.0). 将敏感程度|S|>0.5作为敏感参数用于调整，敏感度阈值0.5是根据模型的机理结构及模拟效果综合率定的，以此为阈值调整参数能够获得的最优模拟结果.

本研究开发的新型数据同化算法将参数敏感性分析耦合到集合卡尔曼滤波过程中，使其能够精确定位并调整每阶段模型敏感参数，实时有效校正模型运行轨迹，提升模型模拟精度. 综合考虑集合卡尔曼滤波对参数的调整过程以及每一阶段参数敏感性分析的时效性，本研究提出的新型数据同化算法运行分3个步骤：预测、分析与更新(表3).

①预测：与集合卡尔曼滤波数据同化的预测步相同，根据上一时刻状态变量(即叶绿素a浓度)后验集合，使用湖泊藻类动态模型模拟该时刻状态变量先验集合(式(1))，对先验集合求期望(式(5))即可得状态变量的模拟值，该模拟值在该时刻实测数据可用之前都有效.

②分析：使用扰动分析法定位该时刻敏感参数. 根据扰动分析法流程，本研究对湖泊藻类动态模型每个待分析参数的扰动范围为：±1%、±5%、±10%、±15%、±20%，共扰动10次. 使用(式(6))计算出该时刻每个参数的敏感度S，将敏感度|S|>0.5作为敏感参数输出到更新步.

③更新：当该时刻实测数据可用时即进入更新步，使用集合卡尔曼滤波更新状态变量和敏感参数集合. 先更新状态变量，根据(式(7))更新状态变量集合，状态变量先验集合被更新为后验集合，对其求期望(式(10))即可得该时刻状态变量的同化值；再更新敏感参数，由于耦合了参数敏感性分析，每一步需要更新的参数维度不同，因此将参数维度固定为一维，然后依次调整，如有多个参数处于敏感状态则依次执行调整参数步(式(11))，如没有参数处于敏感状态则不执行调整参数步. 考虑到集合卡尔曼滤波的假设是各参数误差相互独立且服从高斯分布[11]，因此涉及到多个敏感参数需要调整时，依次调整每个参数效果等同于同步调整；然后使用(式(13))对所有参数集合求期望即可得该时刻模型参数的同化值. 该时刻状态变量和参数的同化值将作为模型下一时刻预测步的初值，依此递推，运行流程如图3所示.

图3 新型数据同化算法流程图[18]Fig.3 New data assimilation algorithm flow chart[18]

表3 新型数据同化算法公式*

1.5 数据同化方案设计

本研究提出的新型数据同化算法以集合卡尔曼滤波为主体改进而成. 为测试其在传统集合卡尔曼滤波基础上的提升效果，同步设计基于传统集合卡尔曼滤波数据同化算法方案用于对比分析. 目前集合卡尔曼滤波在水文水质模型中主要有2种同化方案，一是仅同化状态变量[35]，二是同步同化状态变量和模型参数[18]. 为详细对比差异，分别将这两种方案应用到模型查看其对模型的提升效果. 同时，还需一种完全凭借湖泊藻类动态模型的模拟方案作为评价上述3种数据同化方案效果的基准. 因此，本研究共有了4种方案，包括1个纯模型方案和3个数据同化方案(仅同化状态变量、同步同化状态变量和模型参数及新型数据同化算法方案)，下面详细介绍4种方案的策略及运行步骤.

1)Reference：不使用数据同化算法，仅依据湖泊藻类动态模型模拟叶绿素a浓度. 将2020年1月1日实测的水质数据和2020年1月2日的气象数据作为初值输入，将该阶段模拟的叶绿素a浓度作为下一阶段模型的初值，依此递推，持续模拟至2020年6月1日. 该方案旨在了解湖泊藻类动态模型本身的模拟精度，为3种数据同化方案的模拟值提供对比基准.

2)EnKF_A：使用集合卡尔曼滤波数据同化算法同化状态变量(即叶绿素a浓度)，不同化模型参数. 输入初值时使用蒙特卡洛方法分别对状态变量和边界条件添加误差并生成集合，模拟出下一阶段叶绿素a浓度集合，对集合求期望即可获得模拟值. 当获得叶绿素a浓度实测值时，使用集合卡尔曼滤波同化状态变量集合，对集合求期望获得同化值，作为模型下一阶段状态变量输入，依此递推.

3)EnKF_B：使用集合卡尔曼滤波数据同化算法同步同化状态变量和模型参数. 考虑到使用的湖泊藻类动态模型参数众多，仅同步同化一个参数，即Umax(藻类最大生长速率)，其为模型主控方程参数，是模型初值阶段最敏感的参数. 初值输入时还需要同步生成待同化参数集合，模拟过程同上方案相同，当获得叶绿素a浓度实测值时，使用集合卡尔曼滤波同步同化状态变量和参数集合，分别对集合求期望获得状态变量和参数的同化值，作为模型下一阶段状态变量和该参数输入，依此递推.

4)EnKF_C：使用本研究开发的新型数据同化算法同步同化状态变量和敏感参数. 考虑到湖泊藻类动态模型参数较多(18个参数)，全部用于敏感性分析影响同化效率，因此选取其中8个总体较为敏感的参数，用于新型数据同化算法方案中模型每一阶段的敏感性分析，表4列出了用于敏感性分析的8个参数及其初值. 其中p4(藻类最大生长速率)即为同步同化模型参数方案(EnKF_B)的同化参数，该参数是模型主控方程的参数，在初始状态是模型最为敏感的参数，其余7个参数也是模型各模块的主要控制部分. 因此，通过分析上述8个参数的敏感性能表征模型的总体敏感程度. 新算法初值输入时同步生成待分析敏感度参数集合，模拟过程依然相同，当获得叶绿素a浓度实测值时，先使用扰动分析法定位该阶段模型的敏感参数，然后使用集合卡尔曼滤波依次同化状态变量和敏感参数集合，分别对集合求期望获得状态变量和敏感参数的同化值，作为模型下一阶段状态变量和敏感参数输入，依此递推.

表4 敏感性分析的8个参数[29]

Tab.4 Eight parameters for sensitivity analysis[29]

编号参数描述单位初值p1ϑ温度因子1.08p2α水及非藻类吸收短波辐射的平均消光系数m-10.45p3K藻类沉降速率m/d0.0864p4Umax藻类最大生长速率d-11.145p5GRmax浮游动物最大捕食速率d-10.09p6kr藻类呼吸引起叶绿素a减少速率系数d-10.17p7Topt最适藻类生长的水温℃27p8ke藻类排泄引起叶绿素a减少速率系数d-10.01

以上4种方案中，Reference为纯模型模拟方案，其模拟值作为评价3种数据同化方案对模型精度提升效果的基准；EnKF_A和EnKF_B为传统集合卡尔曼滤波数据同化算法2种主要应用方案；EnKF_C即为本研究提出的新型数据同化算法.

1.6 数据同化效果评价

为评价模拟精度，采用纳什系数(Nash-sutcliffe model efficiency,NSE)衡量模拟值和实测值的符合程度；采用均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)和平均绝对百分比误差(mean absolute percentage error,MAPE)衡量模拟值和实测值的误差[36].

2 结果与分析

由于集合卡尔曼滤波中测量误差和模型误差两参数无法显式给出[11]. 为保证数据同化效果，先使用数值模拟实验测试；然后依次实施4种方案并根据性能指标评价模拟精度和误差，对比分析4种方案模拟效果.

2.1 数据同化算法参数率定

集合卡尔曼滤波中模型误差和测量误差两参数相互影响，需同步率定[11]. 模型误差主要来源于模型结构、参数及边界条件误差等[37]，为合理评估模型误差，使用模型模拟值与实测值计算8个自动监测站MAPE，取其中最小值(10%)和最大值(50%)作为模型误差率定区间边界；测量误差主要来源于测量仪器及环境(气温、风力等)条件等，综合考虑仪器精度及测量过程，测量误差率定区间边界取定为1%～10%. 同步率定时使用RMSE评价数据同化算法模拟误差，RMSE取值越小说明同化效果越佳. 根据数值模拟结果所示(图4)，当模型误差和测量误差分别取18%和3%时，数据同化效果最佳，由此即确定了集合卡尔曼滤波模型误差和测量误差取值. 研究表明集合卡尔曼滤波过程中集合个数越多提升效果越好[17]，但考虑到效率问题，本研究中集合卡尔曼滤波的集合个数取定为100，此集合数已被证明在大多数模型中都足够[38]. 集合卡尔曼滤波的初值对同化结果影响不大，因此将模型初始状态的误差设置为20%.

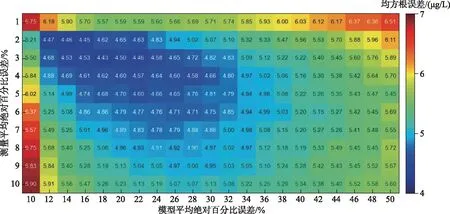
图4 不同模型误差与测量误差背景下的同化结果Fig.4 Assimilation results in case of different models and measurement errors

根据上述讨论，3种数据同化方案中集合卡尔曼滤波的参数如下：模型误差为18%，测量误差为3%，集合个数为100，初始状态误差为20%.

2.2 4种方案结果对比分析

图5展示了8个自动监测站2020年1月1日-6月1日逐日叶绿素a浓度实测值和4种方案的模拟曲线，并给出了4种方案模拟曲线的一项拟合指标(NSE)和3项误差指标(RMSE、MAE、MAPE). 从图5叶绿素a浓度实测值看出，时间上，多数自动监测站叶绿素a浓度峰值出现在4月份；空间上，巢湖西部和南部水域的叶绿素a浓度总体高于东部和北部水域；从叶绿素a浓度极大值模拟看，数据同化后的模拟值大部分略低于实测值，因多数藻类实测的极大值梯度大、回落迅速，模型往往无法及时反应，其模拟值具有滞后性且难以达到峰值高度，经过滤波后会取到一个中间值，因此滤波模拟结果多数略低于实测极大值而又高于模型模拟结果；另外，还需注意蓝藻水华暴发期藻类上浮堆积在水面可能会遮住自动监测探头，监测数据不够准确，存在出现异常峰值的可能. 以叶绿素a浓度实测值为依据，下面详细分析4种方案模拟效果.

1)Reference：模型模拟的叶绿素a浓度曲线仅能够反映实测值大致变化趋势，且在模拟预测叶绿素a浓度峰值上难以发挥作用，模拟结果误差较大. 从性能评价指标得出模型模拟精度在8个自动监测站差距较大，新河入湖区站模拟值的NSE仅为0.1，而东半湖湖心站模拟值NSE则达到了0.69. 8个自动监测站平均NSE为0.49，平均RMSE为7.31 μg/L，平均MAPE为44%，可见模型总体模拟效果并不理想.

2)EnKF_A：从集合卡尔曼滤波同化状态变量方案模拟曲线看出，经过同化状态变量的模型模拟曲线更加贴近实测值. 从性能评价指标得出，8个自动监测站模拟值的平均NSE提升到了0.63，平均RMSE降低了2.47 μg/L，平均MAPE也降低了9%，说明同化状态变量能够提升模型模拟精度.

3)EnKF_B：从集合卡尔曼滤波同步同化状态变量和模型参数方案模拟曲线看出，相较于仅同化状态变量，同步同化模型参数后模型模拟精度提升有限. 尽管8个自动监测站平均NSE提升了0.08，但注意到其中3个站(湖滨站、东半湖湖心、兆河入湖区)的NSE不增反减，而平均NSE的提升主要来自新河入湖区站，从0.26提升到0.53. 这反映不考虑模型参数敏感性动态变化而对固定参数调整难以有效校正模型运行轨迹，反而会因不当调整参数使同化效果更差，存在给模型模拟带来额外不确定性的隐患.

4)EnKF_C：从本研究提出的耦合参数敏感性分析的新型数据同化方案模拟曲线看出，新型数据同化方案能够更加准确地模拟预测叶绿素a浓度，在上述2种数据同化方案上有了进一步提升. 从性能评价指标得出该方案的模型模拟值平均NSE达到了0.76，平均RMSE为4.27 μg/L，平均MAPE下降到23%. 无论总体上还是在每个自动监测站，考虑了参数敏感性的新型数据同化算法对传统集合卡尔曼滤波数据同化效果都有稳定的提升，对叶绿素a浓度峰值有更加准确的模拟. 考虑到本研究设计的3种数据同化方案参数条件都相同，因此能够确定模型模拟精度的提升来源于新型数据同化算法对敏感参数的实时定位和调整. 这说明耦合了参数敏感性分析的新型数据同化算法能够有效定位模型运行每阶段的敏感参数，调整模型运行轨迹，增加模型稳定性，提高模型叶绿素a浓度模拟精度.

3 讨论

案例测试结果表明：巢湖藻类模型的参数敏感性存在显著的动态变化过程，提出新型数据同化算法能够实时跟踪模型敏感参数，实现模型模拟精度的最大化提升. 在新型数据同化算法方案中，根据每阶段模型模拟值，将待分析敏感性的8个参数依次输入扰动分析模块即可获得其敏感度S. 以湖滨站1-5月参数敏感性的动态变化(图6)为例，p1(温度因子)和p4(藻类最大生长速率)在多数时段敏感度等级都在Ⅲ级(|S|≥0.5，一般敏感)及以上，敏感性总体较高. 尤其是p4，在模型运行时间段有62 d的敏感度都在Ⅴ级(|S|≥1.0，极度敏感)以上，是模型最敏感的参数，但也有39 d处于不敏感状态. 表明：受边界条件等要素影响，参数敏感度在模型运行各阶段不断变化，敏感参数在模型动态运行过程中存在转为不敏感的可能. 其它参数虽多不敏感，但随着模型的运行也有敏感时刻. 例如，p3(藻类沉降速率)在模型运行前20 d都不敏感，但在1月21日变为极度敏感参数(|S|≥1.0)，其在当天敏感程度超过了p4(1.0≥|S|≥0.75)，表明随着模型的动态运行，原本不敏感参数也可能受边界条件影响转为敏感参数.

图6 基于扰动分析法的参数敏感性动态变化过程(湖滨站，参数p1～p8含义见表4)Fig.6 The parameter sensitivity dynamic change process based on the disturbance analysis method (Hubin Station, the meaning of parameters p1-p8 are shown in Tab.4)

通过对比分析可知，新型数据同化算法能够显著提升模型模拟精度的原因在于耦合了参数敏感性分析，使其能够实时定位模型敏感参数并有效调整，校正模型运行轨迹，使模型模拟更加精确. 在本研究的湖泊藻类动态模型应用中，参数敏感性分析方法选择了成熟的扰动分析法，从模型中选取了8个具有代表性参数(表4)用于敏感性分析，定位到敏感参数后使用集合卡尔曼滤波更新敏感参数，实时校正模型运行轨迹. 而传统集合卡尔曼滤波数据同化算法则仅能够调整固定的参数，难以应对模型运行中的敏感参数动态变化，无法有效校正模型运行轨迹，甚至不当的参数调整还会增加模型不确定性. 通过两种模型同化方案(EnKF_B、EnKF_C)中参数值动态变化，能够看出新算法相较于传统算法对模型参数的优化调整过程，考虑到站点多、时序长，图7仅展示湖滨站1月份两种方案中参数值的动态变化率，选择湖滨站是为了方便从图6中同步观察各参数1月份的敏感度. 从图7a看出，由于固定同化参数p4(藻类最大生长速率)，EnKF_B方案仅能且不断的调整该参数，即使是在该参数处于不敏感状态(如1月5日)依然调整，而其它参数即使处于敏感状态也不会进行调整. 而从图7b看出，EnKF_C方案则能够根据模型敏感参数动态变化灵活改变对参数的调整，合理应对敏感参数动态变化. 以p4为例，当其处于敏感状态时(如1月2-4日)会及时进行调整，当其处于非敏感状态时(如1月6日)则不会进行调整. 由此可见，本研究提出的新型数据同化算法正是通过耦合参数敏感性分析，实时动态调整敏感参数，实现模型模拟精度的稳定提升，具有广泛应用前景.

图7 不同数据同化方案(EnKF_B(a)和EnKF_C(b))的参数动态变化(湖滨站，2020年1月，参数p1～p8含义见表4)Fig.7 The change of parameter values for the assimilation strategies of EnKF_B (a) and EnKF_C (b)(Hubin Station, January 2020, parameters (p1-p8) descriptions can be found in Tab.4)

本研究模拟时段为2020年1-5月，主要是由于在5-10月的蓝藻水华暴发期间，藻类水华堆积可能影响探头准确测定，自动监测数据质量受影响；同时，根据孔繁翔等提出的湖泊蓝藻水华形成四阶段理论[39]，本研究模拟时间段(1-5月)主要处于藻类复苏和生物量增加的初期，也是决定全年蓝藻水华情势的重要时期，开展此时段的蓝藻水华预测也有一定意义.

4 结论

本研究通过耦合数据同化算法与敏感参数识别算法，实现了模型敏感参数的实时识别与同化，解决了传统数据同化算法难以适应模型敏感参数动态变化的问题；改进算法应用于巢湖藻类动态模拟，测试结果表明：改进算法实现了湖泊藻类动态模型与高频自动监测数据的实时融合，显著提升了模型模拟精度(模拟误差减少42%)，对藻类峰值的模拟精度提升尤为明显；算法与模型采用松散耦合模式，可移植性强，可应用于其它水生态环境模型的数据同化，随着我国河湖多源监测数据的剧增，算法具有广阔应用前景.