电力计量数据驱动的电力故障预测方法研究

付卿卿

(贵州电网有限责任公司， 贵州，贵阳 550002)

0 引言

随着我国经济的发展和社会的进步，我国终端数据的接入量和采集量逐渐地上升，尤其是电力计量数据的积累呈现高储备的趋势。每天仅电力计量数据的积累就高达上亿，故障问题也随之频繁发生，因此需要有效的电力故障诊断模型从储备的电力计量数据中挖掘潜在的规律，科学准确地预测电力故障问题。电力故障的有效预测也可以帮助企业提高电网的运行效率，节约维护过程中所需的成本。针对该领域的研究正处于发展的阶段，部分专家学者[1-2]利用回归分析法建立预测模型，从多因素预测角度出发，分析因素变量间的相关性，判定不同因素对电力故障的影响。也有部分专家[3-4]学者从电力计量数据的角度出发，利用电力计量数据得到计量系统网络阻抗与电流互感器一次、二次侧短路故障之间的关系，将得到的规律应用在故障检测中，但是并没有真正地实现预测智能化，更好的还是将规律和主观经验判断相结合，再将判断后的经验用于预测。还有部分专家学者[5-6]利用人工智能技术建立诊断模型，旨在从海量的电力计量数据中挖掘潜在的规律，但是模型更多是在理论上构建，并未真正地实现故障的诊断，也未真正地将模型搭建起来。

综上可知，目前利用电力计量数据实现电力故障的预测是一种大的趋势，主要集中在知识经验判断、数据理论模型分析等方面。这些诊断方法十分依赖人工操作和专家的经验，而采集海量的数据时，电力计量终端极容易出现问题，故障情况经常发生。因此，本研究利用优化的Tradaboost回归算法建立电力故障预测模型，从大量的电力计量数据中挖掘潜在的规律，实现电力计量数据驱动。

1 故障分析

电力计量数据的获取主要通过电度表、电压互感器、电流互感器，并获取二次侧电流。对于高压电力计量系统故障性质深入分析可知，将故障分为直接可诊断的故障和间接可诊断的故障。直接可诊断的故障即直接通过电力仪表的测量结果，判断是否可以直接发生，并不需要深入的研究潜在的故障特性。间接诊断的故障指电力计量数据长期储存后，通过相应的模型算法可以实现对故障的提前预测，因为电力计量数据是多维度数据的综合，因此可以在主观观测不到的情况下实现提前预测的功能。根据高压电力计量系统的结构，对计量回路的多个参数进行检测和电力实时监测样本的采集。将历史数据和实时监测的数据输入神经网络预测模型中，实现对监测情况的提前预测，对故障问题进行处理和分析。

2 LR优化Tradaboost回归算法

在积累了大量的电力计量数据的基础上，为解决Tradaboost算法权重初始化策略，利用LR()算法进行优化，为得到源域中与目标域数据分布类似的数据集，以类似度为标准对数据进行权重初始化，本文引入LR算法来优化Tradaboost源样本权重初始化步骤，将数据先通过LR算法进行筛选。LR算法的本质是二分类概率输出器，通过LR算法分类后，可以认为更加靠近决策边界的源域数据与目标域数据类似程度更高。假设源域数据分布为a，标记为0，目标域数据分布为b，标记为1。训练LR模型，将得到分类概率，这个概率即可作为源域数据与目标域数据特征分布的类似程度。因此，LR被分类器判定为b的源域数据的初始权重更大。

原始Tradaboost算法是分类模型，子学习器为弱分类器，本文涉及的电力故障预测是回归问题，因此需要子学习器换成SVR回归器代替弱分类器。定义训练集为(xi,yi),i=1,…,l,是xi∈Rn，l为数据总量，n为影响因素维数，xi∈Rn为输入值，yi=R为输出期望值。其目标回归函数为

f(x)=ωφ(x)+b

(1)

式中，φ(x)为输入空间到特征空间的非线性映射，ω为权重向量，b为优化参数。再添加回归损失函数ε，如式(2),SVR即可进行回归预测。

(2)

如式(2)损失函数所示，若预测值与期望值的绝对差小于ε，即视预测值为正确，反之则认为预测错误。SVR算法引入了松弛变量ξi和惩罚系数C，优化目标函数如式(3):

(3)

引入拉格朗日乘子法可得式(3)最优解：

(4)

算法的步骤如下。

输入：SVR回归器，Ds,Dt,Test,μ,ρ,H。

输出：预测故障发生的程度，基于目标域的强回归器f(x)。

Step 1 源域样本权重初始化。合并源域和目标域训练集Ds和Dt，对训练集数据进行归一化。调用LR算法进行Tradaboost源样本权重初始化，为源域中同目标域数据分布类似的数据赋予更大的初始权重。

Step 2 初始化源域样本更新方式Ø(s)，ns为源域样本总量。

(6)

Step 3 设置迭代次数H。Forth=1,2,3,4,…,H。

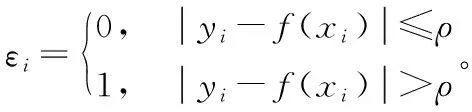
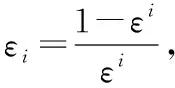
Step 6 计算暂定强学习器f(x)在目标域训练集Dt上的误差εi。

Step 7 重置Dt样本权重更新方式。

(7)

Step 8 计算暂定强学习器f(x)在源域训练集Dt上的误差εi，更新合并训练集样本权重ωi+1。

(8)

ωi+1=ωi+1Ø(t+1)

(9)

Step 9 得到的源域样本权重如小于样本排除参数值μ，则排除该样本，不参与下一次迭代。

Step 10 迭代次数m>M，结束循环，输出最终强学习器。

3 实例应用

将电力计量数据输入到LR-Tradaboost算法中，再将目标域前20组数据和源域全部数据合并成训练集对模型进行训练，将目标域后7组数据作为测试集验证模型预测性能。为验证传统机器学习模型在电力故障预测问题上的适用性，将不同方法下的训练结果进行对比。SVR算法训练集为目标域前20组数据，测试集为目标域后7组数据。同时，为验证LR-Tradaboost算法在预测性能方面的作用，利用针对回归问题的Tradaboost-R2算法同LR-Tradaboost算法的训练结果作以比较，Tradaboost-R2算法的训练集和测试集与LR-Tradaboost算法相同。选用回归算法评价指标均方根误差RMSE以及R2作为算法训练结果的评价指标，对比不同算法测试集预测结果的均方根误差以及R2来对模型进行对比和评价，实现算法预测性能的验证。见表1。

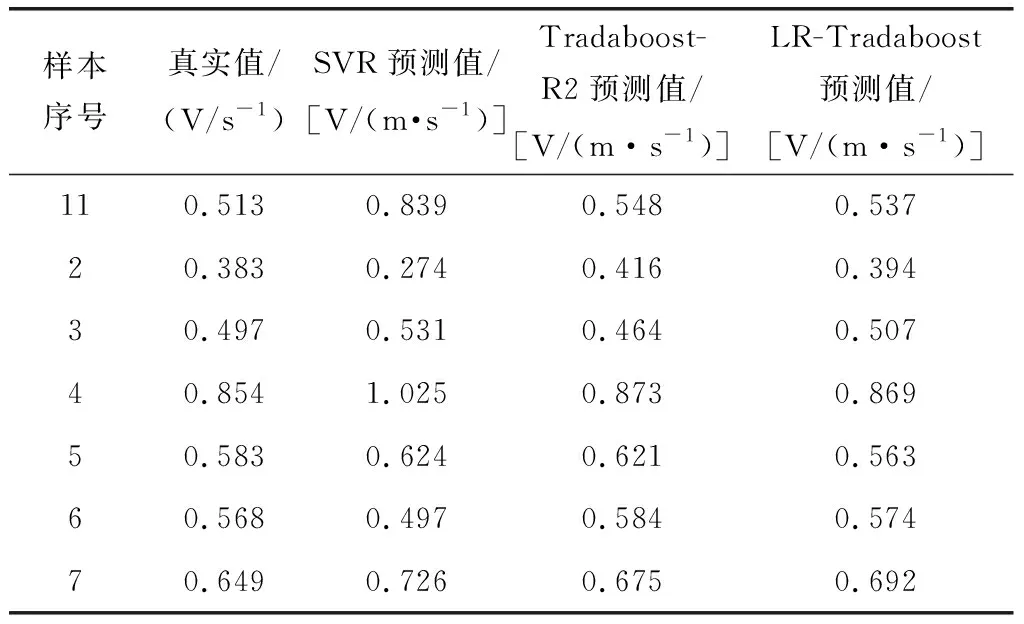
表1 电力计量数据发生异常的真实值与预测值对比表

为了对比LR-Tradaboost算法和Tradaboost-R2算法的学习效率，在2种算法的训练过程中，每隔10次迭代过程，分别计算2种算法得到的暂定强学习器的R2，得到算法的收敛程度。图1为LR-Tradaboost算法和Tradaboost-R2算法的回归收敛速度的对比图。由图1得到，LR-Tradaboost算法在迭代次数为50时已经收敛，模型分数R2达到了0.81，之后的迭代过程中R2不再增加。基于得到明显的收敛程度变化趋势和减少计算工作量的考虑，本研究采用每10次迭代计算一次算法R2，实际上LR-Tradaboost算法的收敛发生在迭代次数40到50的闭区间内，并非在第50次迭代后达到收敛。由图2可得，Tradaboost-R2算法在进行50次迭代后，模型分数仅为0.21，且仍处于上升趋势，事实上Trada-boost-R2算法在100到110次迭代之间才完成收敛。对比2种算法的收敛速度，发现LR-Tradaboost算法的收敛速度几乎是Tradaboost-R2算法的2倍，证明了LR-Tradaboost算法在利用电力计量数据预测电力故障上效果更好，基于LR的优化权重初始化策略有效提高了算法性能及效率。

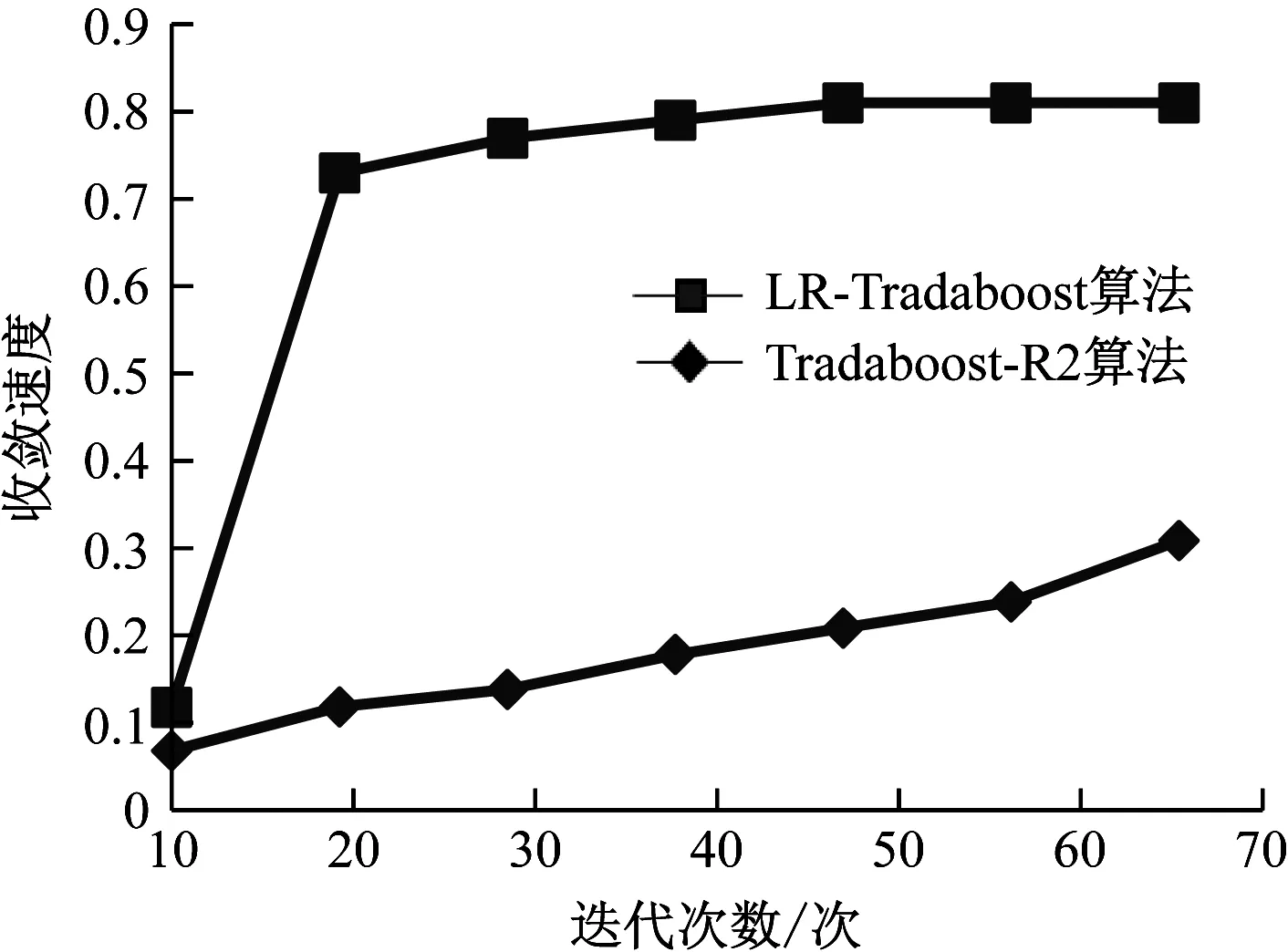
图1 算法回归收敛对比图

4 总结

本研究主要利用电力计量数据结合优化Tradaboost回归算法实现电力故障的预测，提出了LR算法优化权重初始化策略的LR-Tradaboost算法，同Tradaboost-R2算法预测结果和收敛速度作对比,LR-Tradaboost预测误差比Tradaboost-R2少，而收敛速度LR-Tradaboost几乎是Tradaboost-R2的2倍,故LR-Tradaboost算法在电力故障预测中效果较好。