分布式吊舱机翼建模与气动弹性分析

程毅, 余智豪, 赵金瑞, 周云

(中国直升机设计研究所 直升机旋翼动力学重点实验室, 江西 景德镇 333001)

带吊舱的大展弦比机翼的气弹动力学问题是太阳能飞行器、重型倾转旋翼机、分布式多桨机翼和分布式推进垂直起降飞行器设计研究中需要重点关注研究的。分析机翼的气弹响应时，其结构几何非线性效应不能忽视。对于分布式吊舱机翼，在吊舱的集中质量及惯量和飞行气动载荷作用下，机翼会有更大的弯曲和扭转变形[1]，结构上的变形又对飞行载荷产生较大影响，形成结构/气动耦合现象，使得机翼气弹特性产生显著变化[2]。

自20世纪70年代开始，国内外就有大量科研人员对大变形悬臂梁变形和动特性等问题展开理论计算和试验研究。Dowell为验证中等变形梁模型的精确性，在1974年进行一系列大变形情况下的均匀悬臂梁静动态试验，被称作Princeton梁试验[3-4]，该试验后来成为评价非线性梁理论正确与否的标准。Tang和Dowell[5]采用H-D方程[6]，对带配重的悬臂梁机翼(Tang机翼)模型开展风洞试验，之后Arena[7]采用B-L理论对文献[5-6]结果进行验证。Patil[8]采用本征梁和修正非线性理论模型对大展弦比机翼的气弹动力学问题进行分析计算。Steven等[9]采用双重网格MSC Nastran和雷诺平均N-S的FUN3D2种空气动力学计算方法对分布式多桨机翼进行气动弹性分析。James等[10]针对分布式电动多桨机翼结构设计进行研究，提出一种动力学驱动的准-逆设计方法。NASA近几年也开展了分布式电驱动垂直起降飞行器(VTOL)的探索研究[11-12]。国内在大展弦比机翼理论建模和分析研究上仍处于学习跟踪阶段，建模方法主要有中等变形梁理论和商用软件等。谢长川等[13]采用线性化方法计算飞行及突风状态下大展弦比机翼非线性变形，研究结构非线性变形对机翼固有特性及气弹动特性的影响。付志超等[14]采用本征梁和有限入流理论模型对大展弦比机翼的几何非线性气弹动特性进行研究。至于分布式多桨机翼研究国内尚属理论研究阶段。

针对带有分布式吊舱的大展弦比机翼，本文基于中等变形梁和准定常理论模型对分布式吊舱机翼气动弹性进行计算。首先对Tang机翼[15]进行分析，在考虑重力的影响下计算该机翼气弹动特性，计算结果与文献[5,15]吻合，证明本文采用理论模型和分析方法的正确性。沿机翼展向位置添加分布式吊舱，忽略吊舱气动力对机翼影响，研究吊舱参数对分布式吊舱机翼颤振的影响，最后采用时域积分法计算不同飞行速度下分布式吊舱机翼的时域响应，研究其气弹动特性。

1 分析方法

分布式吊舱机翼在飞行状态下会产生较大的结构变形，气动载荷的大小与方向会随机翼的变形而发生变化，且与机翼各剖面处的气流速度有关。故在气弹求解时，需通过机翼坐标变形前后的转换关系描述机翼上的位移和气动载荷。本文基于拉格朗日坐标系，相对翼根坐标系描述机翼上任一点在惯性坐标系中的位置形变，并采用Hamilton[16]原理推导机翼的动力学方程，其表达式为

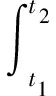
(1)

式中:δU为机翼应变能;δT为机翼动能;δW为机翼外力虚功。

1.1 结构模型

将机翼简化为弹性梁,机翼上变形前后任一点的坐标分别为(x,0,0)和(x+u,v,w),其转换矩阵为TDU,其中u,v,w分别为该点位移形变。

机翼应变能δU

(2)

机翼动能δT

(3)

1.2 气动模型

翼型的气动力计算是在翼型剖面坐标系中进行的,对于弹性机翼来说就是在机翼变形后坐标系中进行的,翼型剖面相对气流速度来自于:①来流速度VW;②机翼运动Vb的贡献。得到气流速度为

(4)

机翼变形坐标下气流速度

(5)

通过推导机翼来流速度分量,采用片条理论,计算剖面气动载荷为

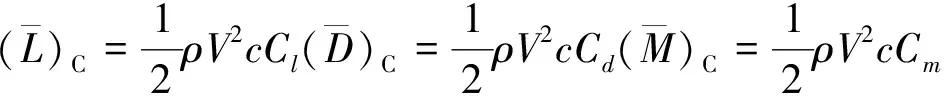
(6)

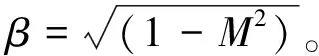
(7)

Λ为来流速度UR引起的扭转角,ed为气动中心到弹性轴的间距。有如下近似公式

sinα≈α, cosα≈1,α=-UP/UR, sinα=UR/UT

因此,在机翼未变形坐标系下的环量气动力为

(8)

翼型剖面的气动合力等于准定常环量气动力和非环量气动力的叠加,即是

(9)

则外力虚功及其变分可写为

(10)

1.3 气动弹性方程

耦合结构与气动模型,得到机翼气弹理论模型。对机翼进行有限元划分,将应变能、动能和外力虚功的质量、阻尼、刚度和载荷向量项离散到对应单元结点上,组集得到机翼的气弹动力学方程

(11)

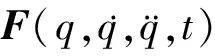
(12)

则由(12)式有

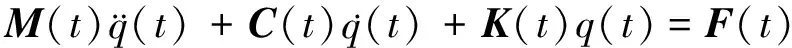
(13)

式中

(13)式可以写为

(14)

式中：I是N×N单位矩阵；0是N×N零矩阵。

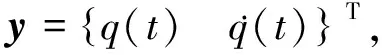
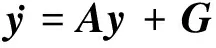
(15)

式中

即可得到一个2N阶微分方程。(15)式只有在M(t)不奇异时才成立。令F(t)=0即G=0,求解(15)式的特征值,特征值的实部代表了模态阻尼,而虚部代表该模态的频率,由此分析机翼的气弹稳定特性。

2 计算结果

2.1 Princeton梁

本文选用Princeton悬臂梁作为结构模型验证算例,梁的结构参数和试验方法见文献[3-4],采用本文的结构模型开展理论计算,计算结果与试验结果[3-4]如图1所示。

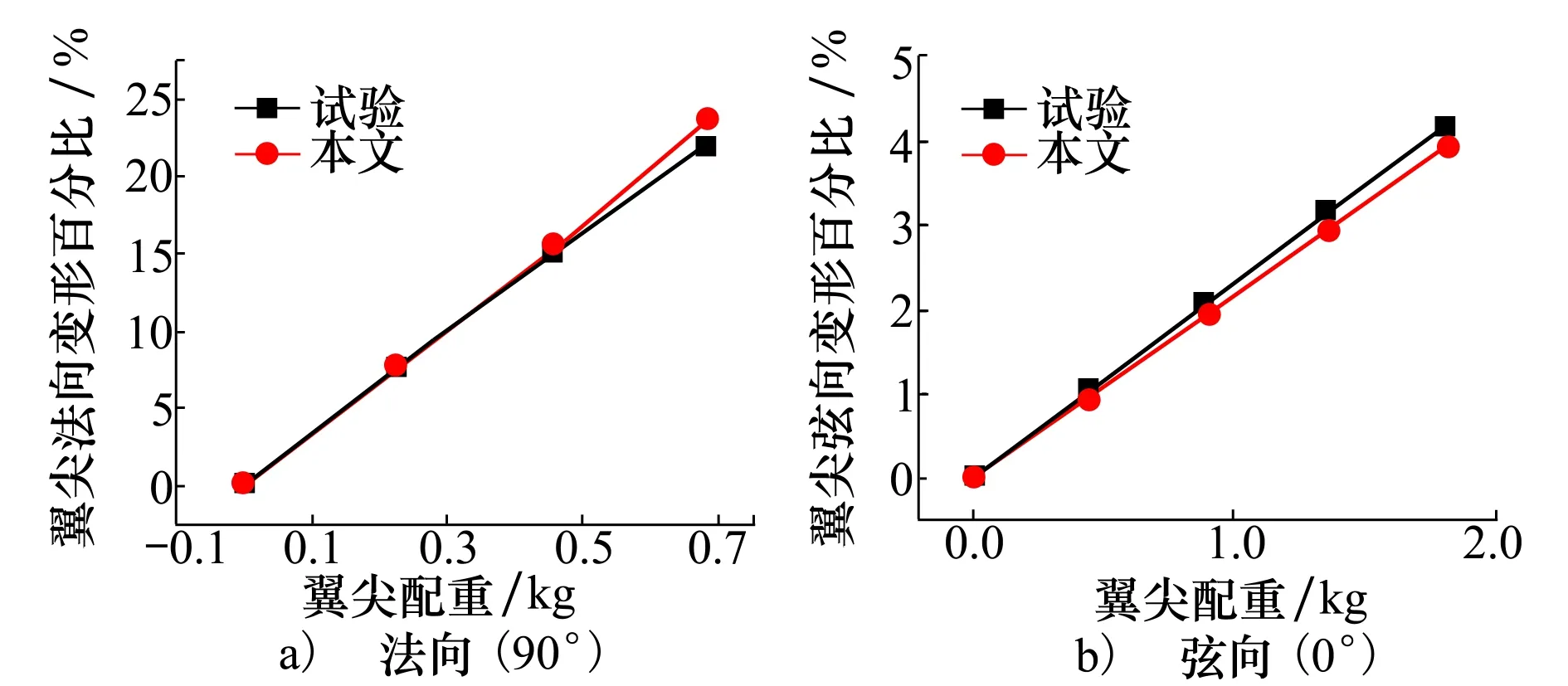
图1 梁尖端静变形

从图1可以发现,梁尖端在受到法向(90°)和弦向(0°)方向载荷时,本文方法计算的法向和弦向位移与试验相符合,验证本文结构模型的准确性。

2.2 Tang机翼

采用本文模型和分析方法对Tang大展弦比机翼进行气弹分析,其结构参数如表1所示。

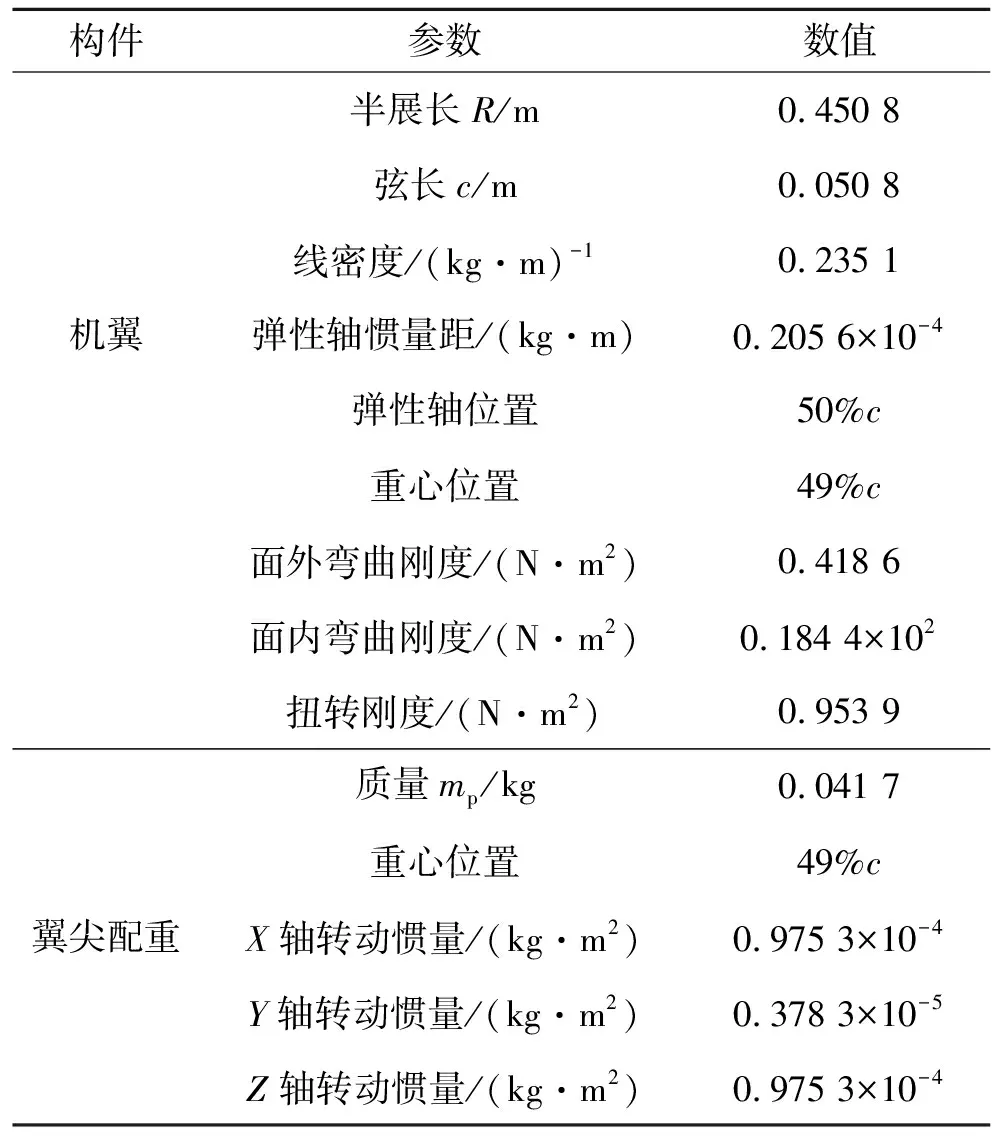
表1 Tang机翼结构参数

对Tang机翼进行固有特性分析,结果如表2所示,计算结果与Arena理论和试验结果[7]相对误差都在5%以内,说明本文结构理论模型是正确的。

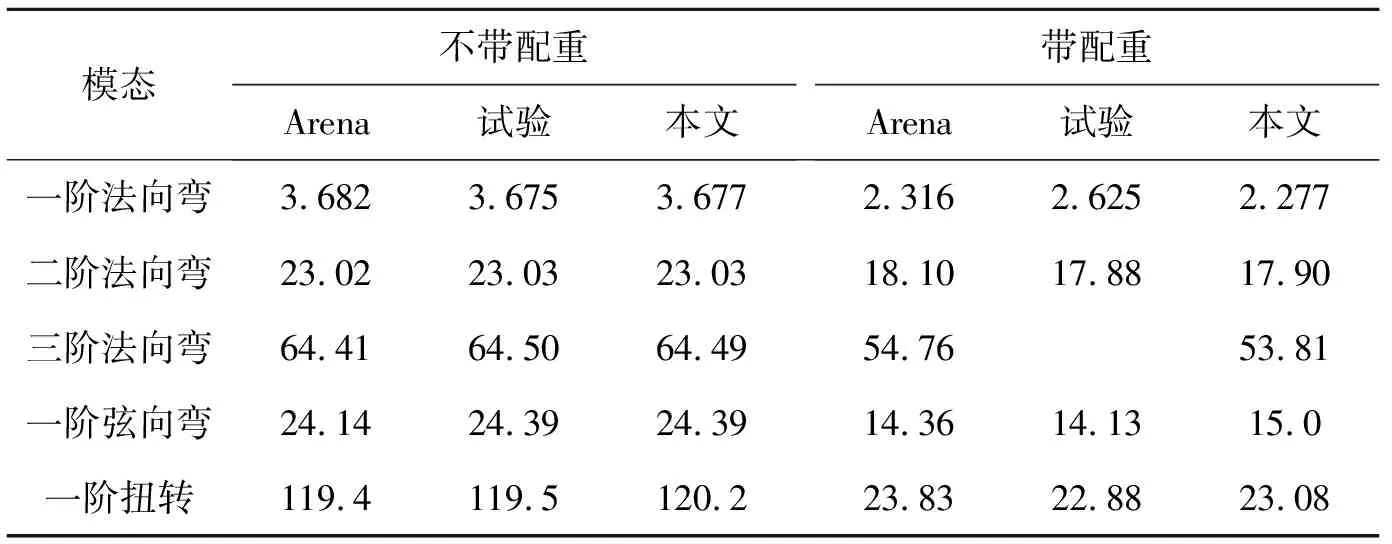
表2 Tang机翼带和不带配重固有频率对比 Hz

接下来验证气弹模型,采用本文分析方法对Tang机翼进行气弹分析,同时考虑机翼和吊舱重力及惯性的影响。利用牛顿-拉斐逊方法,分别对1°和2.2°攻角不同飞行速度下机翼平衡位置的气弹响应进行计算,其求解结果如图2所示。

图2 翼尖响应与飞行速度的关系

由图2可知,本文计算的翼尖法向和扭转响应随飞行速度的变化曲线与Tang和Arena的理论及试验结果基本一致,仅在2.2°攻角且高速飞行(大于30 m/s)时,翼尖扭转角与Tang的理论和试验结果略有误差,Tang理论和试验结果大于本文和Arena计算的结果。但本文和Arena结果是吻合的,说明本文气动模型在中低速下与试验结果更符合。

在图2中机翼平衡位置对(14)式求解其特征值,得到此处机翼的模态阻尼和模态频率,便可分析机翼气弹稳定性。计算出1°攻角下机翼随来流的阻尼和根轨迹如图3所示。

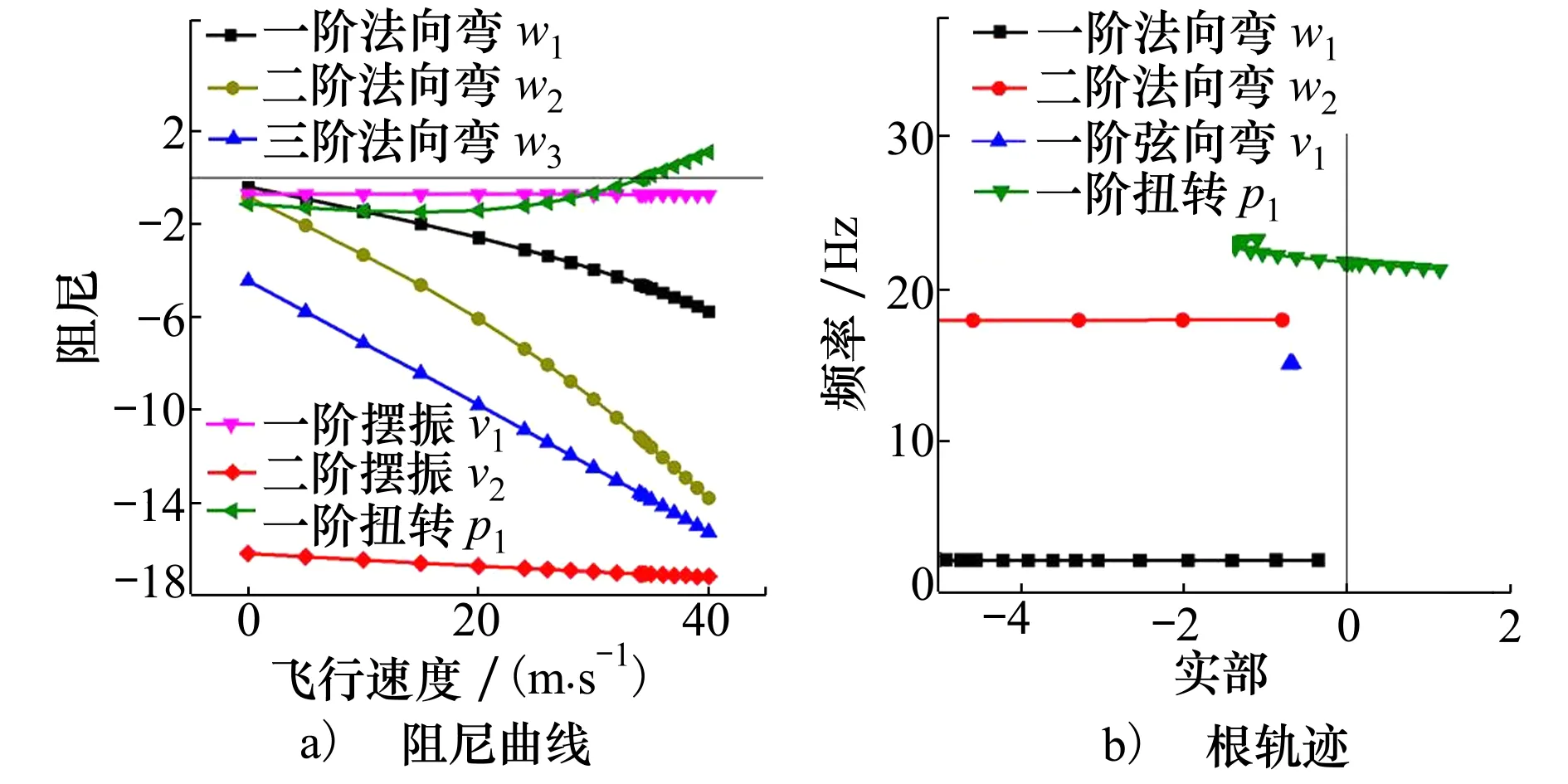
图3 1°攻角下机翼模态阻尼和根轨迹图

从图3可以看出,1°攻角下计算颤振速度Vf为34.2 m/s,颤振频率为21.6 Hz,与试验结果接近。

图4～5为Tang机翼在1°攻角、34.2m/s飞行速度下翼尖时域响应。在颤振速度下,法向和扭转响应均发生简谐振动,且其振动频率一样,说明Tang机翼颤振为面内外弯曲和扭转运动耦合的极限环振动形式。

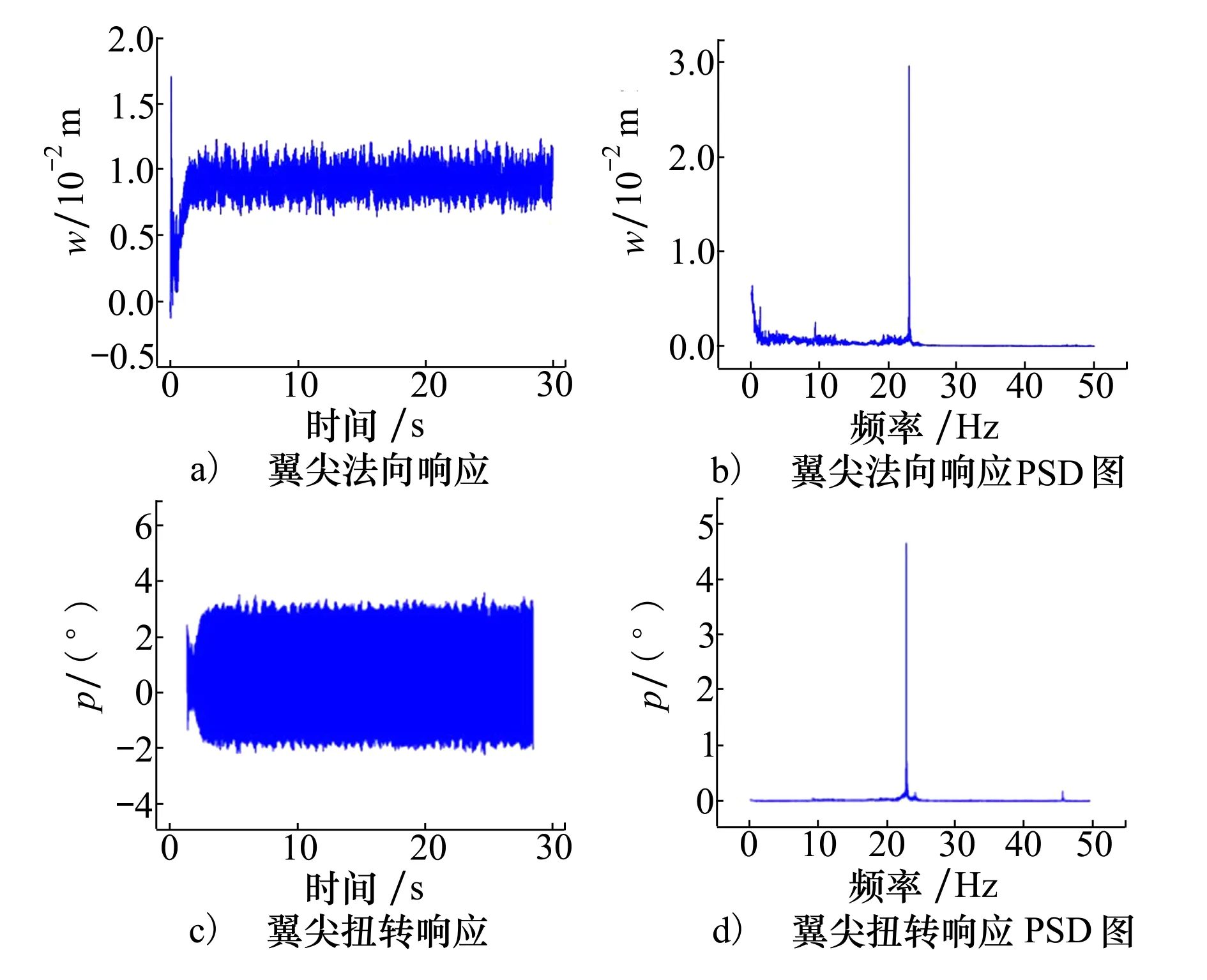
图4 翼尖响应(34.2 m/s,1°攻角)

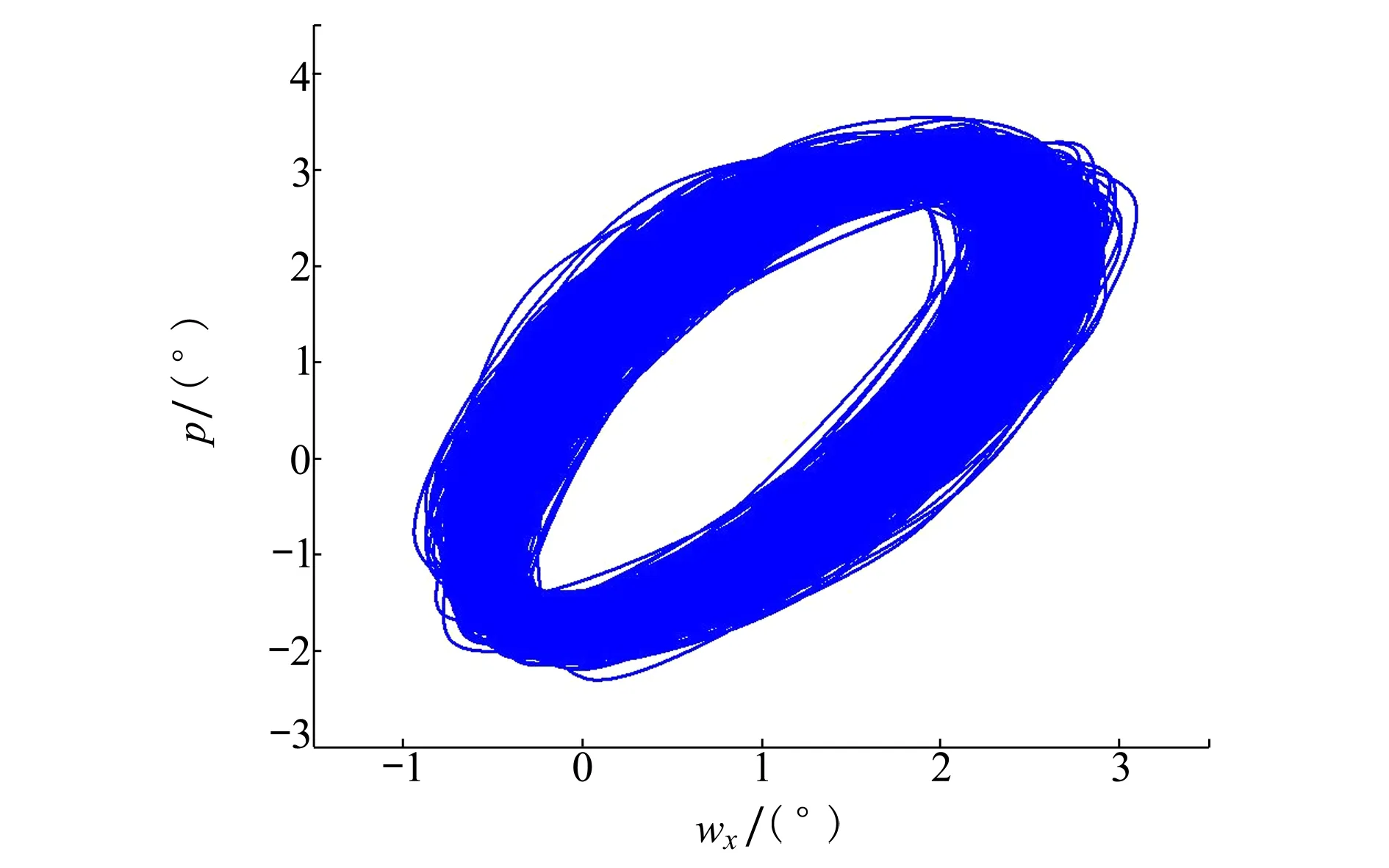
图5 翼尖响应极限环(34.2 m/s,1°攻角)

为了更为广泛地比较,分别对初始攻角为0.25°,0.5°,0.7°,1.0°,1.2°,1.5°,1.7°状态下的机翼开展颤振分析,结果如图6所示。

图6 机翼攻角对颤振速度和频率的影响

从图6可以看出,机翼颤振速度随攻角变大有先变小后变大的规律,在攻角为1°处颤振速度最小;颤振频率在小于1.5°时变化不大,后随攻角变大而逐渐变大;本文计算结果与试验相吻合,说明本文气动模型和气弹计算方法是可靠准确的。

2.3 分布式吊舱机翼

Tang机翼仅在翼尖重心处施加配重吊舱,可用于倾转旋翼构型的机翼仿真分析,但对于近年来发展的电动多桨机翼、分布式多桨机翼、分布式推进垂直起降飞行器等构型就不再适用。因此为研究分布式吊舱机翼的气弹问题,本文在Tang机翼的基础上再添加1个或2个吊舱配重(P2和P3),其中P1始终在翼尖处,P2和P3沿机翼展向分布,考虑吊舱的个数(nr)、质量(mp)、展向站位(y)、弦向(x)和法向(z)偏置等参数对机翼结构和气动的影响,分析研究分布式吊舱机翼气弹动特性。分布式吊舱机翼结构如图7所示。

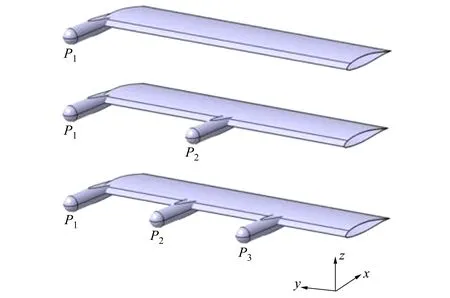
图7 分布式吊舱机翼结构示意图

吊舱质量范围为(0.2mp,1.5mp),展向分布范围为(0.3R,0.85R),重心弦向和法向坐标分别在(-1c,0c)和(-0.8c,0c)之间;忽略吊舱气动力的影响,研究分布式吊舱机翼准定常状态下的气动弹性问题。

分布式吊舱机翼的固有频率计算结果见表3,表中nr=2时，短舱分布在0.5R处，nr=3时，短舱分别分布在0.4R和0.7R处。可见随吊舱个数增加,机翼固有频率都有所降低,说明机翼上的外挂对固有特性有很大影响,尤其是对于分布式多旋翼飞行器,需要重点关注机翼与旋翼短舱耦合后可能发生的结构和气弹动力学问题。

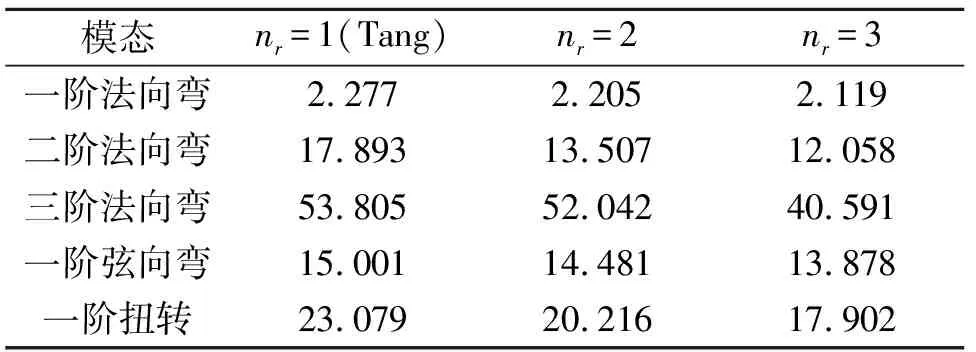
表3 分布式吊舱机翼和Tang机翼固有频率对比

2.2°攻角不同吊舱质量下机翼颤振速度和频率如图8所示。吊舱无法向和弦向偏置,从结果可以看出:①随着吊舱的质量增大,nr=1时颤振速度先减小后变大,变大是由于吊舱惯性及其产生的低头力矩影响变大。②nr=2时若P1和P2质量同时改变,颤振速度一直减小; 若只有P2质量变化时, 颤振速度却逐渐变大,这是因为吊舱惯性及低头力矩和P2使得机翼整体质量分布更均匀的影响。③对于机翼颤振频率,随着吊舱的质量增大机翼颤振频率都逐渐减小。

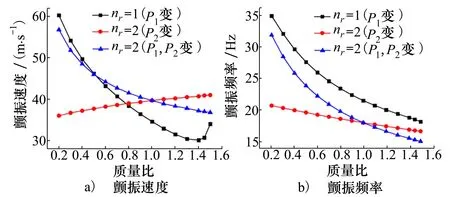
图8 吊舱质量对颤振速度和频率的影响(2.2°攻角)

nr=2时,2.2°攻角下P2不同展向站位和弦向偏置下机翼颤振速度如图9所示。此时P2质量为0.02 kg,无法向偏置,从结果可以看出:①P2在0.5R处时机翼颤振速度是最大的,而越处于两端特别是靠近翼根时颤振速度反而是减小的,说明机翼集中质量和载荷的分布不均会使系统稳定性下降;②随着弦向偏置增大,即吊舱向前缘方向偏置增大时,P2在0.5R处时,颤振速度也随之增大,说明此时吊舱的低头力矩会提高机翼的稳定性;P2在靠近翼根时颤振速度是先变小后变大的,但是在靠近翼尖时是一直变小的,说明此时质量分布的不均匀性对稳定性的影响大于吊舱的低头力矩。

图9 展向站位和弦向偏置对颤振速度的影响 (nr=2,2.2°攻角)

2.2°攻角下,nr=3时不同弦向偏置(无法向偏置)下机翼颤振速度如图10a)所示,不同法向偏置(无弦向偏置)下机翼颤振速度如图10b)所示。其中P1质量为0.041 7 kg、P2和P3质量为0.02 kg,从结果可以看出:①随着弦向偏置增大,颤振速度也增大;②P2和P3越靠近0.5R处机翼颤振速度越大,而越处于两端颤振速度反而是减小的;③随着法向偏置增大,即吊舱向机翼下方偏置增大时,颤振速度也随之增大,说明吊舱对机翼产生的惯性矩会提高机翼稳定性。

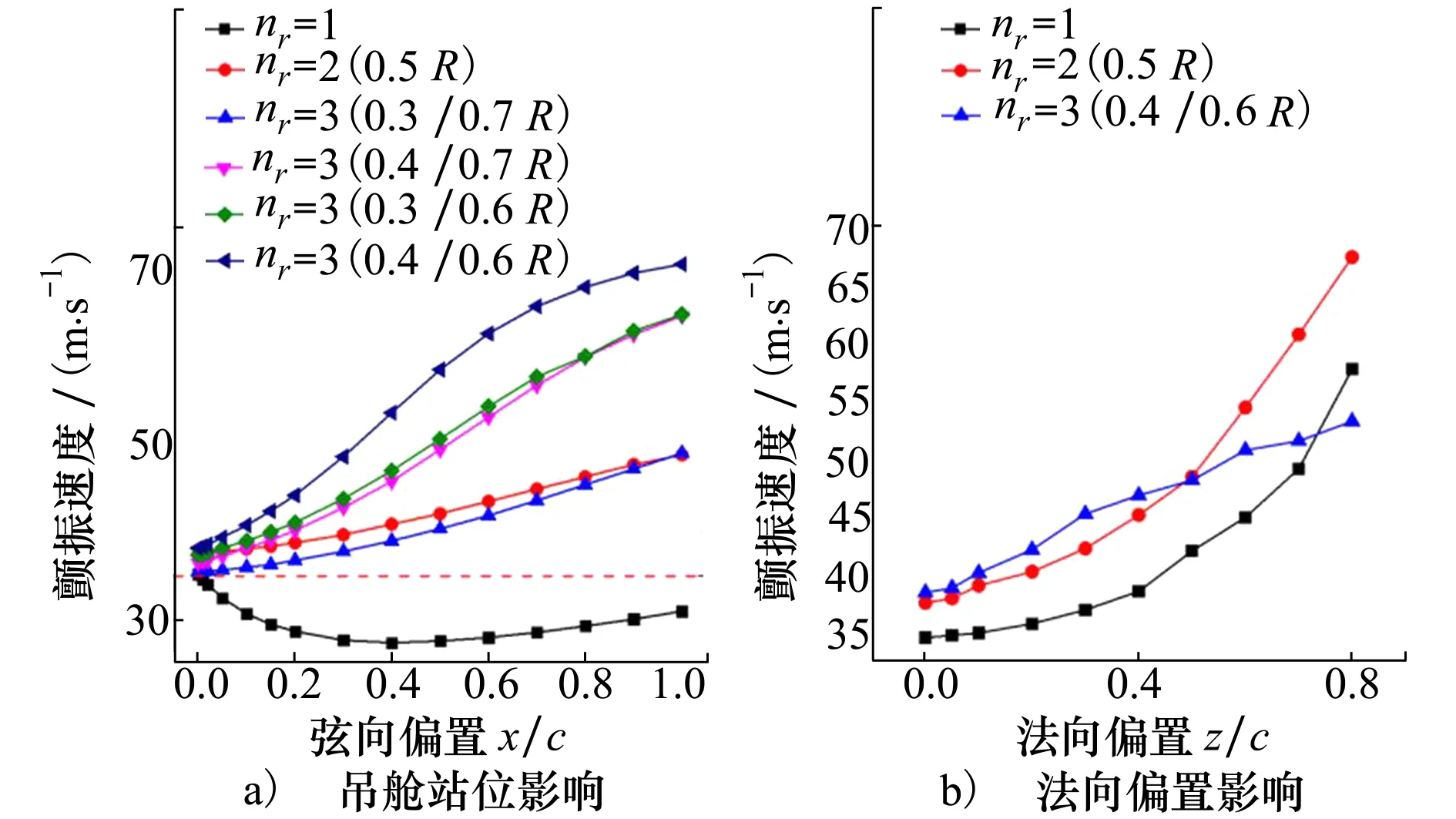
图10 2.2°攻角下机翼颤振速度

以nr=3,P2和P3分别在机翼0.4R和0.7R处,P1质量为0.041 7 kg,P2和P3质量为0.02 kg,吊舱无法向和弦向偏置的分布式吊舱机翼为标准模型。计算1°攻角飞行速度小于30 m/s、等于36.2 m/s、略大于38 m/s和大于45 m/s，临界颤振速度Vf(36.2 m/s)情况下的分布式吊舱机翼气弹响应时域响应,计算结果如图11～15所示。

图11 翼尖响应(30 m/s,1°攻角) 图12 翼尖响应(36.2 m/s,1°攻角)

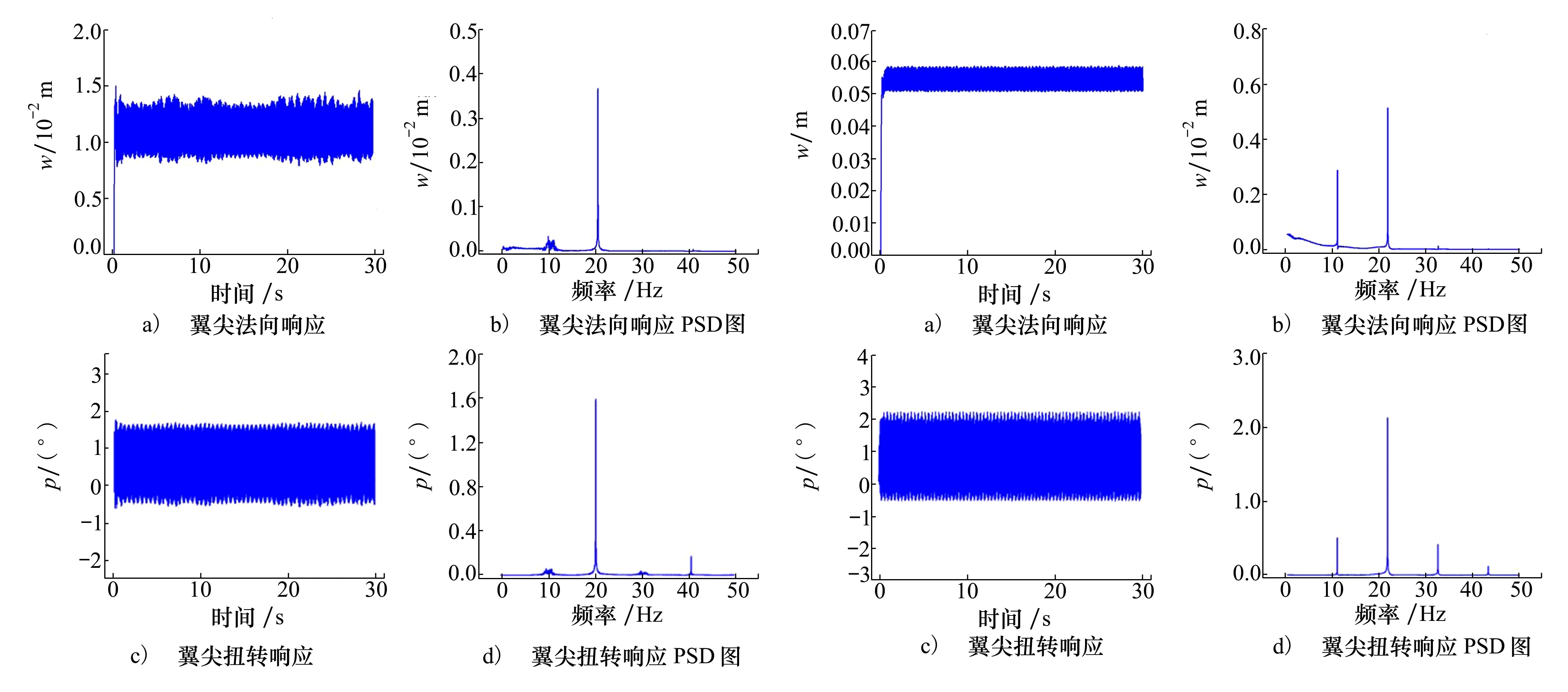
图13 翼尖响应(38 m/s,1°攻角) 图14 翼尖响应(45 m/s,1°攻角)

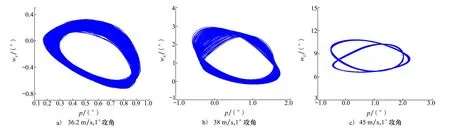
图15 翼尖振动极限环

从响应时域曲线可以发现：随飞行速度逐渐变大，分布式吊舱机翼的法向和扭转变形也逐渐变大，其模态频率渐渐靠近，直到发生颤振，此时法向和扭转响应都产生简谐振动。说明分布式吊舱机翼颤振为面内外弯曲和扭转运动耦合形式。

随飞行速度逐渐变大，在小于颤振速度时，机翼响应经历了振动收敛形式；在等于颤振速度时，机翼响应振幅较小，机翼呈现了小幅单频振动形式；在略大于颤振速度时，机翼响应振幅变大，机翼呈现大幅单频振动形式；在飞行速度大于颤振速度(45 m/s)时，机翼二阶法向弯曲模态频率(21.7 Hz)正好为一阶法向弯曲模态频率(10.8 Hz)的2倍，同时由于面内外弯曲和扭转运动发生了耦合，使得机翼极限环出现分岔，翼尖响应相图呈现出2个极限环，此时机翼出现倍频简谐振动形式。当飞行速度进一步增大时，机翼极限环将会出现更多倍频或多频简谐振动直至发生机翼颤振发散现象。

分布式吊舱机翼的颤振模式表现为面内外弯曲和扭转运动耦合振动，三维效应明显。这正是大展弦比柔性机翼气弹动特性的特点。

3 结 论

本文基于准线性化隐式建模方法，采用中等变形梁模型和准定常理论，利用小扰动和有限差分法，建立大展弦比机翼的动力学模型。通过对Tang机翼和分布式吊舱机翼的气弹动特性开展分析计算，得到以下结论：

1) 对悬臂梁模型，静变形计算结果与试验相吻合，验证结构模型的准确性。

2) 计算Tang机翼气弹动特性，表明本文气弹模型是准确有效的；Tang机翼的颤振为面内外弯曲和扭转运动耦合形式；随机翼攻角变化，颤振速度先变小后变大，且在1°攻角处最小，而颤振频率变化不大。

3) 对分布式吊舱机翼，随吊舱质量增大颤振速度和颤振频率都减小，而只改变P2(或P2/P3)质量时，颤振速度反而略有变大；吊舱P2(或P2/P3)越靠近0.5R处颤振速度越大，在此条件下一定范围内弦向和法向偏置越大颤振速度也越大；机翼集中质量和载荷的分布不均会使系统稳定性下降。

4) 分析分布式吊舱机翼气弹时域响应计算结果可得，随飞行速度逐渐变大，分布式吊舱机翼经历了振动收敛、小幅单频振动、大幅单频振动、倍频简谐振动形式；分布式吊舱机翼的颤振形式一样是面内外弯曲和扭转运动耦合，三维效应显著。