增材制造Ti-6Al-4V合金断裂行为与应力三轴度关系研究

高柏森, 黄玮, 王生楠, 张霜银, 陈先民

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.中国飞机强度研究所 科研管理部, 陕西 西安 710065)

增材制造(additive manufacturing,AM)是一种以粉末或丝状材料为原材料,使用逐层堆叠方式,从数字模型直接构造复杂实体的制造技术[1]。增材制造技术作为一种新型的先进制造技术,较传统的成型工艺有着制造时间短、材料利用率高、所需设备少的优点。按照成型原理,增材制造技术可分为激光增材制造(laser additive manufacturing,LAM),电子束增材制造(electron beam additive manufacturing,EBAM)和电弧增材制造(wire and arc additive manufacturing,WAAM)。而得益于近年来工艺设备等的成熟和进步,LAM中的选区激光熔融(selective laser melting,SLM)技术制造的钛合金(Ti-6Al-4V)构件在航空、航天、生物医疗等领域得到了较为广泛的应用[2]。Ti-6Al-4V合金作为一种典型的α+β型钛合金,其典型的组织由外延生长的粗大β柱状晶组成。由于增材制造成型过程中伴随着复杂的物理化学变化和多个物理场的耦合作用,增材制造钛合金构件较钛合金锻造件有着更多的内部初始缺陷,如激光参数、扫描方式、熔池厚度等均会影响如气孔、融合不良、未熔融粉末等缺陷的形成[3]。而这些缺陷导致了增材制造钛合金构件的塑性显著降低。实际使用中,多通过退火处理等方式使组织均匀化,去除残余应力,提高增材制造Ti-6Al-4V合金的延伸率。但是,增材制造钛合金中的初始缺陷难以通过热处理等手段完全消除,导致增材制造钛合金构件在复杂载荷下的力学行为与传统工艺制备的钛合金构件有着一定的差异,难以进行准确预测[4]。Wang等[5]通过CT扫描、显微镜等方式观察了增材制造钛合金材料中的孔洞形貌及尺寸数量分布,Sames、Vilaro等[6-7]发现,通过SLM得到的构件中的孔隙率较传统工艺有着明显的增加,Gu等[8]的研究指出增材制造钢材料的孔隙率在2%～4%之间,此外Biswal等[9]通过扫描电子显微镜(scanning electron microscope,SEM)和CT扫描等方式对WAAM得到的构件进行了研究,发现与传统制造方法相比,材料的孔隙率有显著提升。而这些初始缺陷对构件服役期的安全性造成了严重影响,限制了增材制造材料在更多领域的进一步应用。

与传统制造方式得到的钛合金材料不同,增材制造钛合金材料由于初始缺陷的存在在载荷作用下更容易发生断裂失效,因此研究增材制造钛合金在不同应力状态下的断裂应变将有助于研究其断裂行为,为材料在实际工程中的应用提供帮助[10]。在三维应力空间中,一点的应力状态可以由应力三轴度和洛德角参数来共同描述。在拉伸载荷作用下,应力三轴度对材料的断裂应变起主导作用。得益于有限元仿真技术的广泛应用,一些学者使用试验与数值模拟相结合的方法,利用含有缺口的平板或圆棒等试样[11],研究了应变与应力三轴度间的关系。衣海娇等[12]通过数值仿真与DIC试验方法结合,使用缺口圆棒试件研究了6061-T6铝合金在不同应力三轴度下的断裂应变,采用Johnson-Cook模型描述了6061-T6铝合金的断裂行为。对于钛合金板材的室温拉伸试验,张霜银等[13]使用扫描电镜对增材制造材料的断口及金相进行了观察,分析了断裂发生的机理。

目前,国内外学者主要对传统加工方式的金属材料在不同应力状态下的断裂行为开展了大量研究,而对增材制造钛合金材料的断裂失效研究还比较缺乏。随着增材制造钛合金在各领域内的广泛应用,其韧性断裂行为与应力三轴度的关系亟待研究。本文通过光滑圆棒试件(smooth round bar,SRB)和缺口圆棒试件(notched round bar,NRB)的准静态单轴拉伸试验,借助有限元方法得到断裂时刻试件的应力三轴度和断裂应变,讨论了应力三轴度对增材制造钛合金断裂应变的影响规律;通过扫描电子显微镜观察了断口形貌,研究了试件的起裂位置和断裂机理是否属于孔洞聚合造成的韧性断裂,并对断裂的起始位置与应力三轴度的关系进行了讨论。

1 增材制造钛合金的拉伸断裂试验

1.1 试件的制备

增材制造钛合金试件由Ti-6Al-4V钛合金粉末经EP-M250 SLM 3D打印机制造得到,表1给出了Ti-6Al-4V粉末的组成成分。试件制备完成后,在800℃下静置4 h,并在氩气保护下冷却至室温以消除试件内部的残余应力,然后经机加工得到所需的试件构型和尺寸并对试件表面进行抛光处理。

表1 Ti-6Al-4V粉末成分 %

制备的试件分为2大类。第一类为光滑圆棒试件,通过单轴拉伸试验测量增材制造Ti-6Al-4V钛合金的基本力学性能,得到材料的本构关系用于有限元仿真。第二类为不同缺口半径的一系列缺口圆棒试件(共4组,缺口半径分别为2.5,5,7.5,10 mm),试件长度为160 mm,缺口处最小横截面的直径均为10 mm。不同的缺口圆棒试件通过单轴拉伸断裂试验用于研究增材制造钛合金在不同应力三轴度下的断裂行为。图1和图2分别为增材制造钛合金光滑圆棒试件和缺口圆棒试件的尺寸,其中光滑圆棒试件制备了5件,缺口圆棒试件每组制备3件。

图1 增材制造钛合金的光滑圆棒试件几何尺寸

图2 增材制造钛合金的缺口圆棒试件几何尺寸

1.2 试验方法

增材制造钛合金光滑圆棒和缺口圆棒试件的单轴拉伸试验在陕西省分析测试中心进行,在室温环境下使用Instron-8802液压材料试验机进行试验,为保证准静态加载,设定试验机的加载速率为1 mm/min。试验的位移-载荷曲线由试验机直接输出,位移采用引伸计测量,量程均为5 mm。对于光滑圆棒试件,引伸计的标距为50 mm;对于缺口圆棒试件,引伸计的标距为25 mm。试件在外载荷作用下经过弹性段后,撤下引伸计继续加载直至试件发生断裂。试验过程全程录像,试验后测量试件的断口直径。

1.3 光滑圆棒试验结果

图3显示了全部光滑圆棒试件在单轴拉伸下的位移-载荷曲线。如图3所示,5件光滑圆棒的位移载荷曲线较为接近,说明本文的增材制造钛合金材料力学性能具有较好的一致性。表2给出了本文测得的增材制造钛合金的基本力学性能,弹性模量为119 GPa,屈服应力为896 MPa,极限强度为1 102 MPa,密度为4 430 kg/m3,泊松比的取值来自于艾霄鹏的试验测定结果[14],设定为0.34,这些参数将用于后续的有限元仿真分析。

图3 光滑圆棒试件的位移载荷曲线

表2 增材制造钛合金的基本性能

1.4 缺口圆棒试验结果

全部的增材制造钛合金缺口圆棒试件在单轴拉伸载荷下的位移-载荷曲线如图4所示。在试件最小横截面直径均为10 mm的情况下,缺口半径越小的试件其极限载荷越高,光滑圆棒试件的缺口半径为无限大,因此其拉伸断裂载荷最小。不同缺口试件的弹性段响应大体相近,缺口半径较小试件的塑性段更短,其断裂延伸率更低。在拉伸断裂试验结束后,记录4组12件缺口圆棒试件在破坏时的位移和断裂后的断口直径。基于有限元模拟,试验得到的断裂位移可以用于确定试件在断裂时的缺口处直径,断口直径将用于计算材料在当前应力三轴度下的断裂应变。

图4 不同缺口半径的缺口圆棒试件位移载荷曲线

2 拉伸试验的数值模拟

2.1 有限元模型

缺口试件内部的塑性变形与断裂失效在单轴拉伸载荷下的破坏失效中起着关键的作用,因此需要对试件内部的应力场和应变场进行研究。通过引伸计或DIC方法均难以获得试件内部的应力应变场分布,需要对缺口圆棒的拉伸试验进行有限元仿真,以得到准确的内部应力三轴度和应力应变分布。

本文使用Abaqus有限元软件对缺口圆棒试件的单轴拉伸进行数值仿真,采用C3D8R三维八节点缩减积分单元对试件模型进行划分,并在应力集中的缺口处进行网格细化,缺口处单元尺寸为0.5 mm,对于试件其他部分,单元尺寸为2 mm。根据实际的加载情况,在数值仿真中采用一端固支,一端通过参考点耦合施加位移载荷的加载方式。数值模拟的本构关系采用Mises屈服准则、关联流动法则和各向同性硬化,使用试验测得的塑性应变-真实应力曲线进行输入。然而材料的塑性应变-真实应力响应有一定的应力状态依赖性,需要使用迭代的方法对本构关系进行一定的修正,以消除这种应力状态依赖性。图5给出了经迭代修正后的塑性应力-真实应变曲线和试验值的对比图。将迭代修正后的塑性应力-真实应变曲线输入仿真,得到位移载荷曲线与试验的曲线相对比(如图6所示),拟合效果较好,说明迭代修正获得的本构关系较为合适。表3给出了通过试验和有限元方法测得的断口直径。其中,断口直径使用游标卡尺多次测量后取平均值,游标卡尺的精度为0.03 mm。多次测量的断口直径数值较为接近,说明断口仍保持为圆形。

图5 迭代修正和试验获得的塑性应变-真实应力曲线

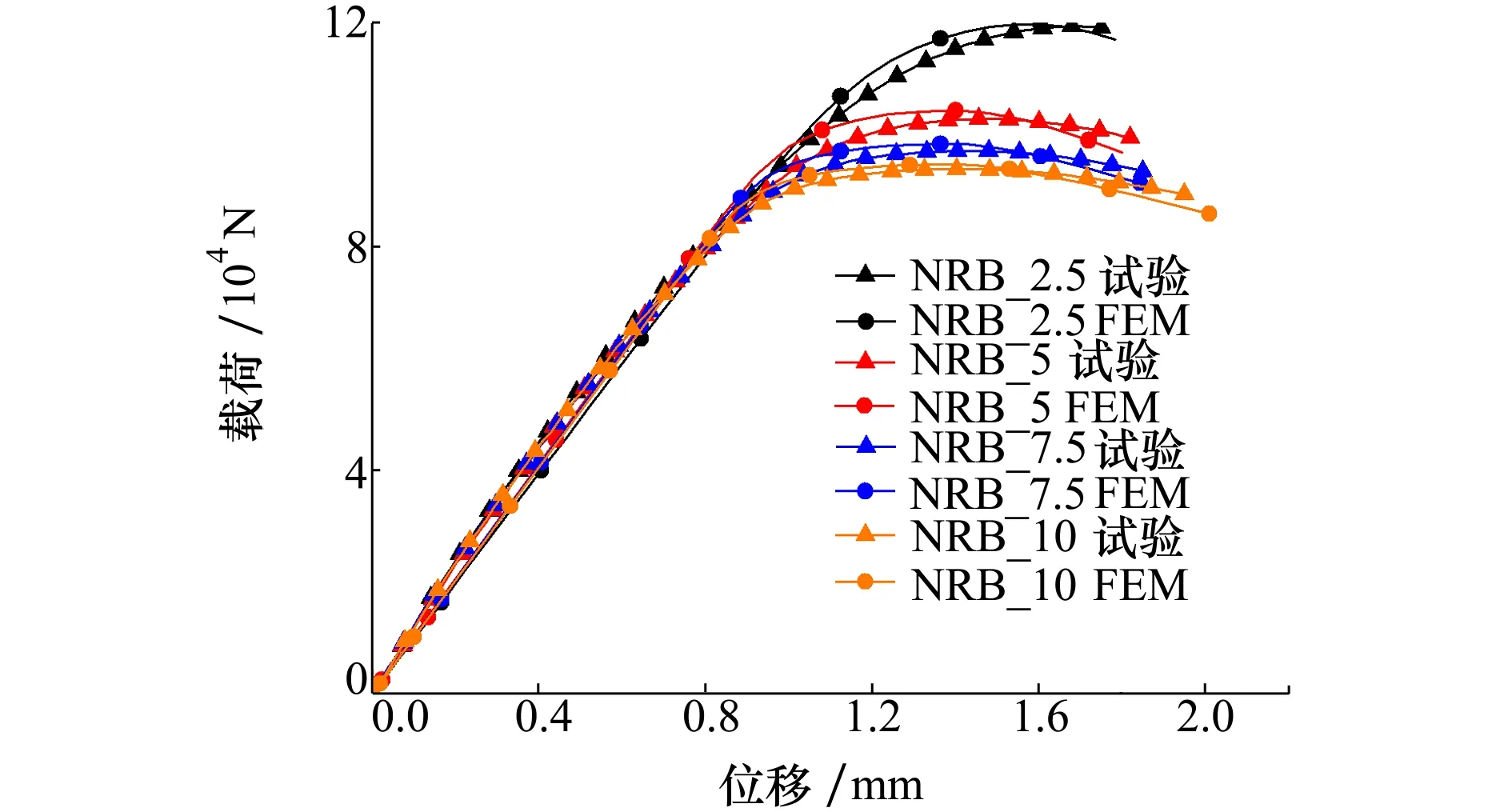
图6 不同缺口半径的增材制造钛合金缺口圆棒试件 在单轴拉伸载荷下的试验与数值仿真结果比较

表3 试验和数值仿真得到的断口直径

2.2 应力三轴度和应力应变分布

Bridgman(1952)[15]经推导得到,缺口圆棒的应力三轴度最大值出现在最小截面的中心处,应力三轴度的数值可由Bridgman公式(1)得到

(1)

式中：T为应力三轴度；a0为最小截面半径;R0为缺口半径。

通过缺口圆棒试件在单轴拉伸载荷作用下的数值模拟可以发现,应力三轴度的最大值总是出现在试件缺口处圆截面的中心。在加载的初始阶段,缺口试件中心处的应力三轴度基本保持恒定。试件的缺口半径越小,试件中心处的最大应力三轴度越大。如表4所列,对于不同缺口半径试件的应力三轴度,在拉伸的初始阶段,有限元仿真结果与Bridgman公式吻合较好。

表4 基于公式和数值模拟的最小截面中心处应力三轴度

但是,随着载荷的继续增加,试件缺口附近将发生显著的塑性变形,塑性应变的累计对应力三轴度的分布有明显影响[16],缺口圆棒试件中心处的应力三轴度也显著逐渐提高,如图7所示。因此,需要借助有限元数值仿真并与试验相结合,以获得增材制造钛合金缺口圆棒试件在断裂时刻的应力三轴度分布。图8显示了不同缺口半径的圆棒试件在单轴拉伸载荷作用下,试件缺口附近的应力三轴度分布。

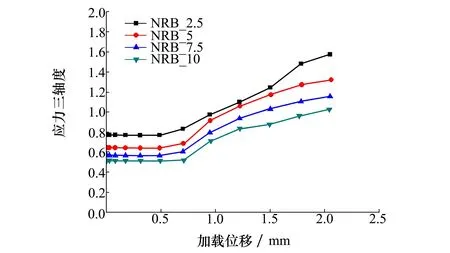
图7 缺口圆棒试件中心处的应力三轴度随加载位移的变化

图8 不同缺口半径的缺口圆棒试件的应力三轴度分布图

由公式(1)和有限元方法分别得到的不同缺口半径试件的应力三轴度如图8和表4所示。断裂时刻对应的应力三轴度相比公式(1)的结果有显著增加,这是由缺口附近的塑性变形造成的。因此使用公式(1)得到的应力三轴度结果有一定误差,只在加载初期较为准确,真实的断裂时刻对应的应力三轴度需要通过有限元方法得到。

塑性应变在初始阶段主要集中于缺口边缘,随着加载的进行,塑性应变集中的位置逐渐转移至最小截面中心处。图9为不同缺口半径的缺口圆棒在加载过程中等效应力分布。有限元结果发现对于较大缺口半径的试件,断裂时塑性应变集中于最小截面中心处;对于缺口半径较小的试件,断裂时塑性应变集中于缺口的边缘处。等效应力的分布与塑性应变类似。对于缺口较小的试件,断裂时的应力三轴度与应力不再同时集中于最小截面中心处,由于应力三轴度与应力集中同时决定着裂纹的萌生扩展,因此断裂的发生将不再与缺口较大的试样一样,起始于最小截面中心处。

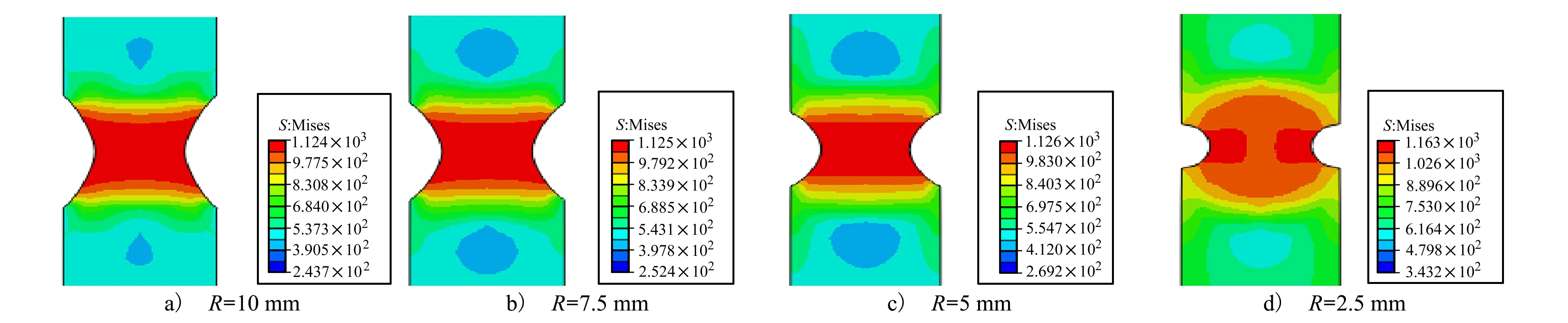
图9 不同缺口半径的缺口圆棒试件的等效应力分布图

2.3 断裂应变的确定

缺口圆棒在单轴拉伸载荷下的断裂应变可以由公式(2)确定

(2)

式中：εf为断裂应变;d0为最小截面的初始直径;dt为断裂后最小截面的直径。

在实际试验中,断裂时刻的断口直径难以准确获得,因此将试验和数值模拟相结合,分别采用3种方法确定缺口圆棒试件在准静态拉伸载荷下的断裂应变。①完全基于拉伸断裂试验得到试件的断口直径,然后通过公式(2)计算得到;②基于试验和有限元模拟相结合,当数值模拟中加载位移等于拉伸试验断裂时刻的位移,获得断裂时数值模拟中试件的断口直径,然后再通过公式(2)计算得到;③完全基于有限元模拟得到缺口圆棒试件在拉伸载荷作用下达到断裂位移时的最大等效应变。

以上3种方式获得的不同缺口半径试件的断裂应变值分别列于表5中。可见随着缺口半径的降低,应力三轴度不断增加,对应的断裂应变值不断降低。试验值与有限元值在缺口较大时差异较小,在缺口较小时差距较大。

表5 不同方法得到的断裂应变值

3 断口形貌分析

将试验后的缺口圆棒试件在保护好断口的前提下进行线切割,对断口部分使用TESCAN VEGA 3扫描电子显微镜进行观察。图10给出了扫描电镜下断口形貌的照片,其中中间为断口的宏观形貌,左侧为断裂起始区域的局部放大图片,右侧为剪切唇的局部放大图片,放大位置在中间宏观形貌图中用红色圆圈进行了标注。

图10 扫描电镜下缺口圆棒试件的拉伸断口形貌

通过对整个断面的观察可以发现,所有试件的断口均为缺口部分横截面积最小处,断口整体呈杯锥状,有着明显的纤维区、放射区和剪切唇。从宏观上看,断裂起始的纤维区较为粗糙,边缘的剪切唇较为光滑。观察断裂起始的区域,可以发现大量韧窝和扩张后的孔洞,这些孔洞包括气孔、融合不良等。这说明断裂起始于微孔洞的扩张、聚合,最终形成裂纹导致断裂。在试件的剪切唇处有着少量的孔洞,表面主要被剪切带所覆盖,有着典型的波浪状花样,说明这一位置是断裂的快速扩展区。这些特征说明全部的缺口圆棒试件都属于韧性断裂。

对于缺口半径较小的试样(R=2.5 mm),断裂起始于应力集中的边缘处,而非应力三轴度较高的最小截面中心处。裂纹从边缘处萌生,并逐渐扩展,直至发生断裂失效。对于其他缺口半径较大的试件(R=5 mm,7.5 mm,10 mm),断裂起始于截面中心处,裂纹由中心处沿径向向四周扩展,最终在边缘处形成剪切唇。

4 结 论

本文通过对光滑圆棒和缺口圆棒试件的准静态拉伸试验与有限元仿真相结合,得出了应力三轴度对增材制造钛合金断裂行为的影响规律。通过扫描电镜对试件拉伸断口形貌进行了观察,分析了断裂的机理。研究发现,本文使用的增材制造钛合金构件力学性能较为稳定,断裂形式均为韧性断裂,断口上发现了如气孔、融合不良等多种激光增材制造初始缺陷。借助有限元方法,确定了缺口圆棒试件的断裂时的应力三轴度和断裂应变,其中缺口半径越小的试件中心处的应力三轴度越高。在中高应力三轴度范围内,增材制造钛合金材料的断裂应变随应力三轴度的升高而降低;对于缺口半径较大的试件,断裂行为均由应力三轴度主导的,断裂也都是从应力三轴度最高的最小截面中心处开始;对于缺口半径较小的试件,应力集中在缺口边缘处,此时应力集中主导试件断裂的发生,断裂将从试件边缘而非试件中心开始。因此,通过不同缺口半径圆棒试件研究不同应力三轴度对材料断裂应变的影响时,试件的缺口半径不能一直减小,应该确保缺口圆棒试件在单轴拉伸载荷下的断裂行为是由应力三轴度主导的,而且初始破坏位置也是在试件的应力三轴度最大处。