全尺寸起落架的气动及声学特性分析

田斯源, 余培汛, 白俊强, 任晓峰, 包安宇, 韩啸

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 无人系统技术研究院, 陕西 西安 710072；3.中航工业第一飞机设计研究院, 陕西 西安 710089; 4.中航工业空气动力研究院, 黑龙江 哈尔滨 150060)

起落架作为支撑飞机着陆载荷，同时在起飞后以运动方式缩回机身以减少阻力的重要部件，其机械结构异常复杂。这些部件上的气流会引起不稳定的表面压力，由此产生的气动噪声被视为类似于偶极子源的噪声，声强与速度的六次方成正比[1]。

针对起落架气动噪声问题，20世纪70年代的开创性实验研究工作提供了最初的见解[2]。然而，由于声学风洞尺寸及测试设备精度等因素制约，早期的起落架声学实验均采用缩比模型或简化模型[3-4]。随着声学实验研究的不断深入，越来越多的研究机构采用全尺寸和更详细的模型[5-6]来捕捉起落架小部件的高频噪声贡献。

高保真度气动噪声数值模拟技术是起落架气动声学问题研究的另一条重要路线。随着计算流体力学(computational fluid dynamics,CFD)、气动声学理论等基础理论的发展，以及计算能力的提升，高保真度的计算气动声学(computational aeroacoustics,CAA)数值方法[7]已成为起落架气动噪声研究中不可替代的重要手段。例如：空客公司牵头，法宇航、德宇航和南安普顿大学联合发布的LAGOON项目，众多学者[8-9]以该起落架标模为研究对象，开展了稳态/非稳态CFD和CAA气动声学数值工具的验证分析。其中，Sanders等[8]采用ZDES/FWH的混合方式，开展了马赫数为0.18，0.23的2个状态起落架固体表面的动压频谱特性及远场总声压级特性研究。而国内胡宁、张凯宁等[10-11]同样采用DES耦合FWH的混合方法针对不同起落架展开研究。此外，在起落架气动噪声数值模拟方面做出出色研究工作的学者有Imamura、Vuillot、刘佩清等[12-14]。

上述声传播大多采用声比拟理论的FWH方程、Kirchhoff方程进行求解。从考虑声传播过程的相互作用以及声波之间的相互影响等角度出发，声比拟理论难以保证噪声空间分布的准确性。本文在中航工业第一飞机设计研究院、中航工业空气动力研究院、西北工业大学联合工作的基础上，以某飞机全尺寸起落架模型为研究对象，开展相关的声学风洞实验和高精度CAA数值模拟研究，其中数值模拟采用了SAS/APE[15]的气动声学混合算法。通过实验数据和数值模拟结果对比，研究分析了全尺寸起落架的时均流场、瞬时流场、声源分布及空间噪声分布特征。

1 气动噪声混合数值方法

1.1 NS控制方程

为了给起落架的噪声传播分析提供可靠的气动噪声源和背景流场结果，流场数值计算采用了可压缩三维雷诺平均Navier-Stokes方程。其曲线坐标下的微分表达形式如(1)式所示

式中：Q为守恒变量。F,G和H分别为笛卡尔坐标系3个方向上的通量项。(2)式给出了直角坐标(x,y,z)与曲线坐标(ξ,η,ζ)之间的三维坐标变换的雅可比矩阵

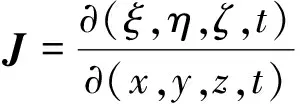
(2)

对于方程的数值离散，利用Roe的迎风通量差分裂技术对对流项和压力项进行了区分，采用van Leer的MUSCL方法确定单元界面处的状态变量插值。剪应力项离散则采用了中心差分格式。

为封闭控制方程，文中采用基于Menter SST模型的尺度自适应模拟(scale adaptive simulation,SAS)模型。该模型的流场划分不依赖于网格尺度的分布，而是由湍流尺度、von Karman长度和局部流动结构等因素共同决定。为了保持SST湍流模型在边界层中的稳定性，进行原ω方程与QSAS项的组合，其中QSAS的表达式为

由(3)式可以看出，Lυk变量可以调整可解的流动结构尺度，避免了高频流动结构阻尼耗散过大问题。SAS模型在远场区起着类似于大涡模拟的作用，过滤尺度由局部流动结构决定。对于本文所使用的SAS模型的准确性，西北工业大学的余培汛等[16]通过SAS模型，采用武器舱空腔标模M219为计算模型，与实验数据对比，完成后续射流对腔内压力脉动的抑制效果的验证,文中将不再对SAS模型进行重复验证。

1.2 声扰动方程

将扰动形式NS方程转化到频率-波数域，对其本征模态进行分离，忽略扰动量的黏性效应，保留仅会激发声学模态响应的部分源项，最后，通过反变换得到时域下的声扰动方程(acoustic pertibation equations,APE)。

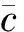
计算气动声学问题不同于常规的计算流体力学问题，使用常规的CFD数值离散格式模拟CAA问题，可能带来巨大的数值误差从而引起不必要的数值噪声，甚至掩盖真实的声场。因此，APE方程数值离散所采用的时间、空间离散须协调一致，满足高精度、低耗散和低色散的要求。文中对于APE方程的时空离散，网格块内部采用了低色散低耗散DRP格式，网格块交接面采用了基于WENO格式的高阶通量分裂算法，时间推进采用了四阶Runge-Kutta格式，远场边界采用了无反射边界。为加速APE方程求解，采用了基于MPI的并行求解技术。对于本文中所使用APE方程求解的正确性，西北工业大学的余培汛等[18]，运用APE方程，计算30P30N前缘缝翼噪声，与德国宇航中心(deutsches zentrum für luft-und raumfahrt,DLR)所开发PIANO计算以及美国航空航天局(national aeronautics and space administration,NASA)实验结果相吻合，文中将不再对APE方程求解进行重复验证。

1.3 气动噪声混合求解框架

起落架气动噪声求解所采用的混合数值方法主要分为三大部分，如图1所示。第一部分为背景流场、声源区扰动变量的计算求解，主要通过RANS求解和SST-SAS非定常求解获得；第二部分为CFD网格上声源及背景流场向CAA网格上的高保真度传递，这里主要通过基于Kd树搜索算法和形函数插值算法获得；第三部分为基于带源项的线化欧拉方程或声扰动方程进行声波的传播，获得整个声辐射场。

图1 气动噪声混合求解

2 实验测试设置

起落架声学实验在中航工业空气动力研究院FL-52声学风洞进行，如图2所示。该声学风洞开口实验段的横截面积为2.0 m×1.5 m，开口最大风速为100 m/s，消声室自由场低限频率为80 Hz。为了准确测量起落架噪声，在来流速度为70 m/s风速条件下进行了7次重复性测量。图3给出壁面90°位置处的声压级频谱重复性，从图中可以看出在整个频段范围内频谱趋势、峰值频率及幅值重复性良好。

图2 实验测试场景

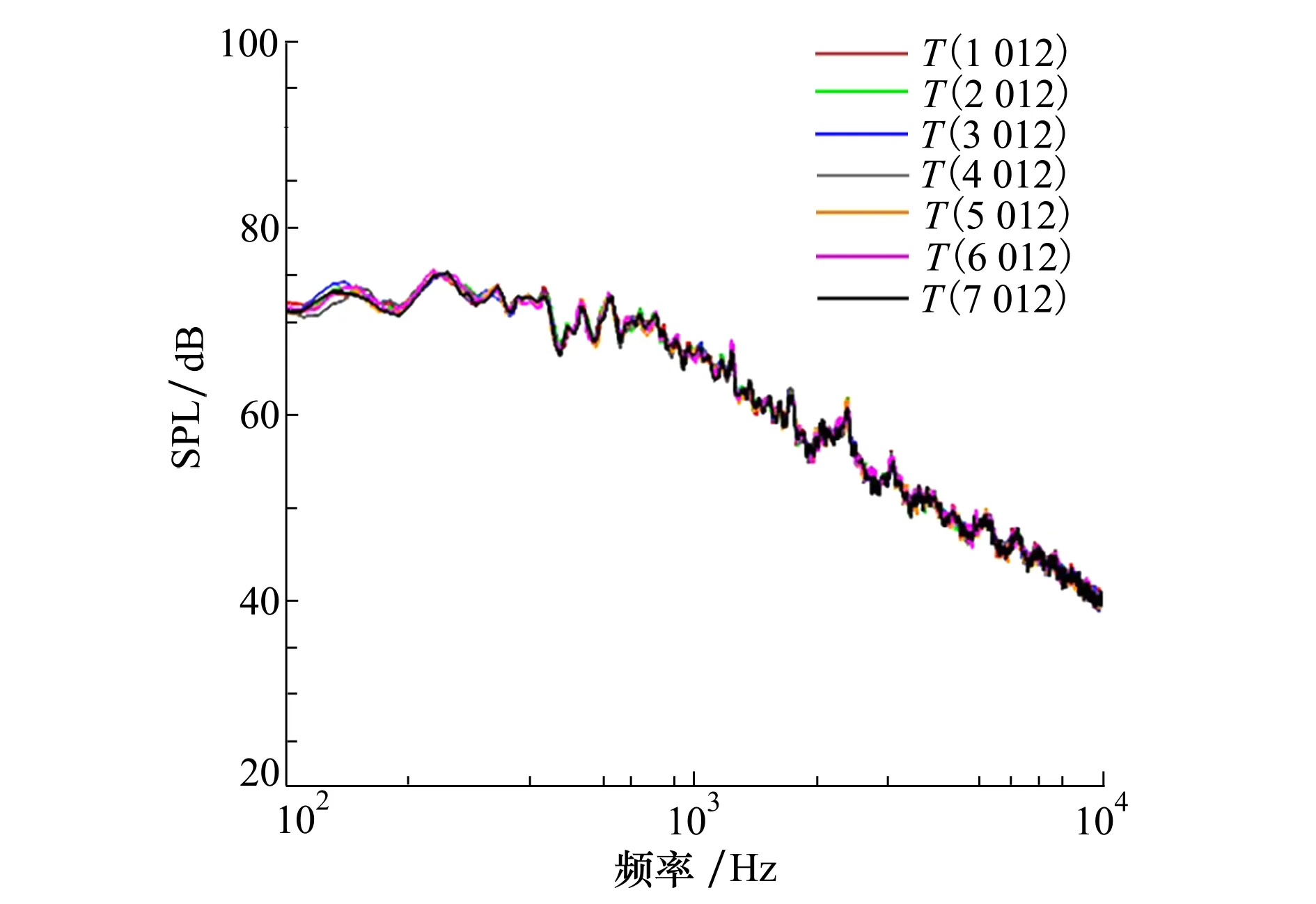
图3 壁面线阵90°位置70 m/s风速下声压级频谱重复性

1) 噪声测试设备：

·1/4 inch自由场麦克风：水平阵面(B&K 4954A)

·表面传声器：模型表面声载荷测量点(SKC SMP47)

2) 气动测试设备：

·脉动压力传感器：XCQ-093-5G脉动压力传感器

·静压测量设备：PSI的ESP-64

3 数值计算设置及网格说明

本文的研究对象为某支线飞机的前起落架全尺寸模型，该起落架主要包含了机轮、扭力臂、活塞杆、横向支撑杆等部件，需要注意的是扭力臂部件为非对称部件，其余部件为对称部件。三维视图如图4所示，起落架正面视角的左侧定义为左侧机轮。

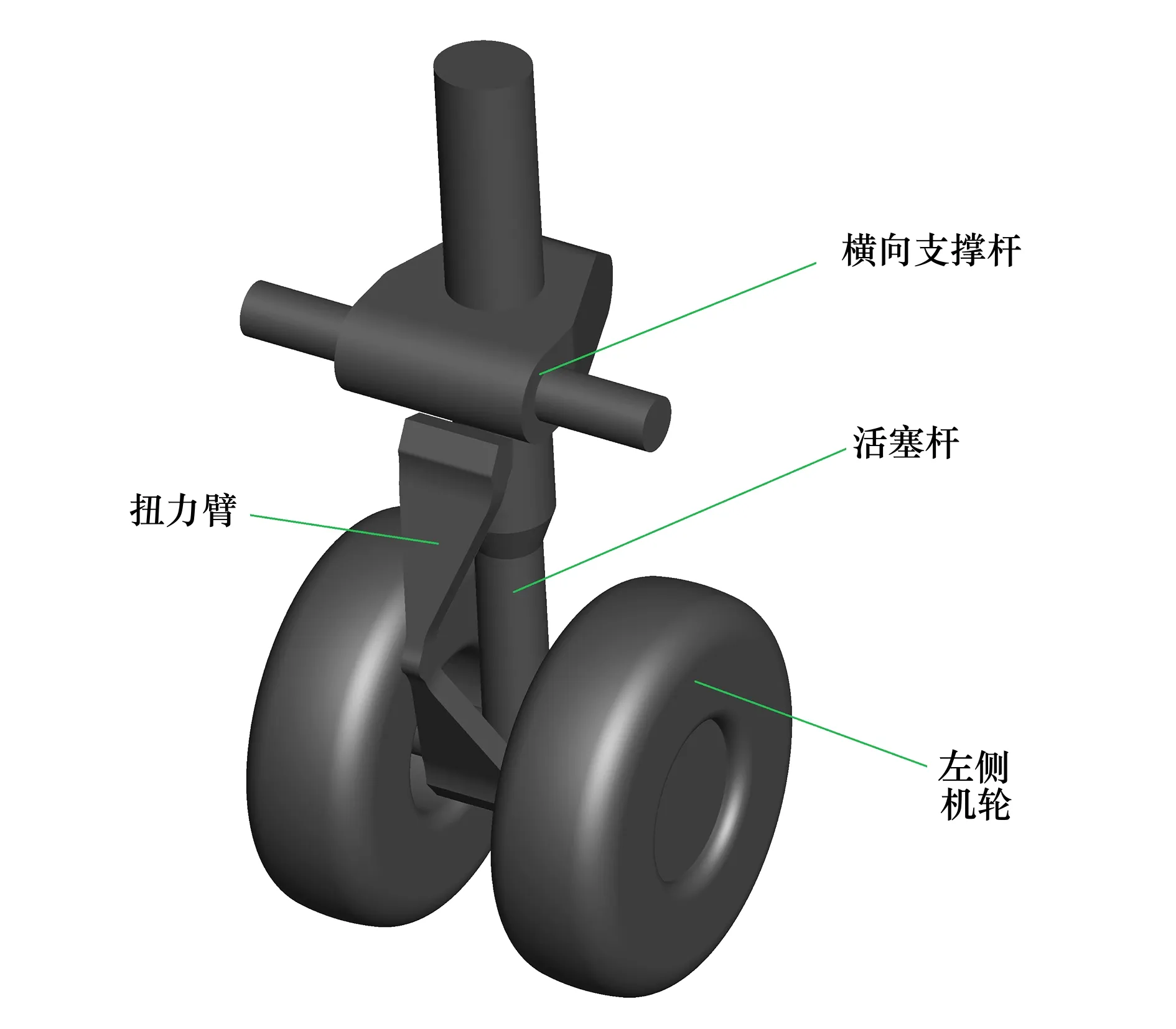
图4 起落架模型说明(单位：mm)

起落架数值风洞实验状态和计算状态均为：来流速度为70 m/s；参考压力为101 325 Pa；来流迎角α=0；侧滑角β=0。为了较精确模拟起落架的流场特征及声场，其CFD网格及CAA网格均采用了ICEM软件生成的多块结构网格形式，其中，CFD网格生成中采用O型网格模拟附面层，附面层第一层网格尺度为D×5×10-7(其中D为轮子的直径)，附面层生长率为1.1。

在计算CFD结果之前，先对网格无关性进行验证，选取网格单元数为3 000万,8 000万,10 000万和17 200万的网格进行非定常状态下的CFD计算。不同网格量下的阻力系数(Cd)如表1所示，其中阻力系数计算公式为

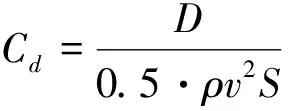
(6)

在该表达式中，设置S=1。

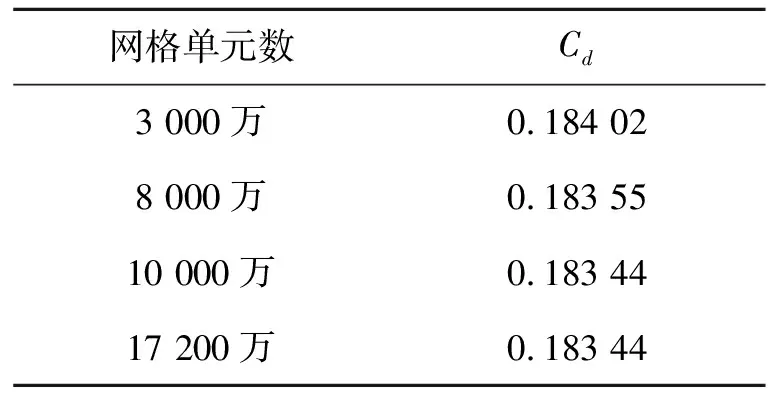
表1 不同网格单元数所计算的阻力系数

可以看出其阻力系数随着网格单元数的增加收敛性更好，并且10 000万网格单元数与17 200万网格单元数所计算阻力系数值一致，由此证明网格收敛性较好。在网格无关性验证完毕后，为保证起落架尾迹部分精度，CFD网格单元数最终选择为17 200万，网格切面细节如图5a)所示。CAA计算域大小约为CFD计算域的1/2，CAA网格该采用了球形远场和矩形近场，便于生成具备优异正交性和长宽比的网格，网格节点约为8 000万，网格切面细节如图5b)所示。

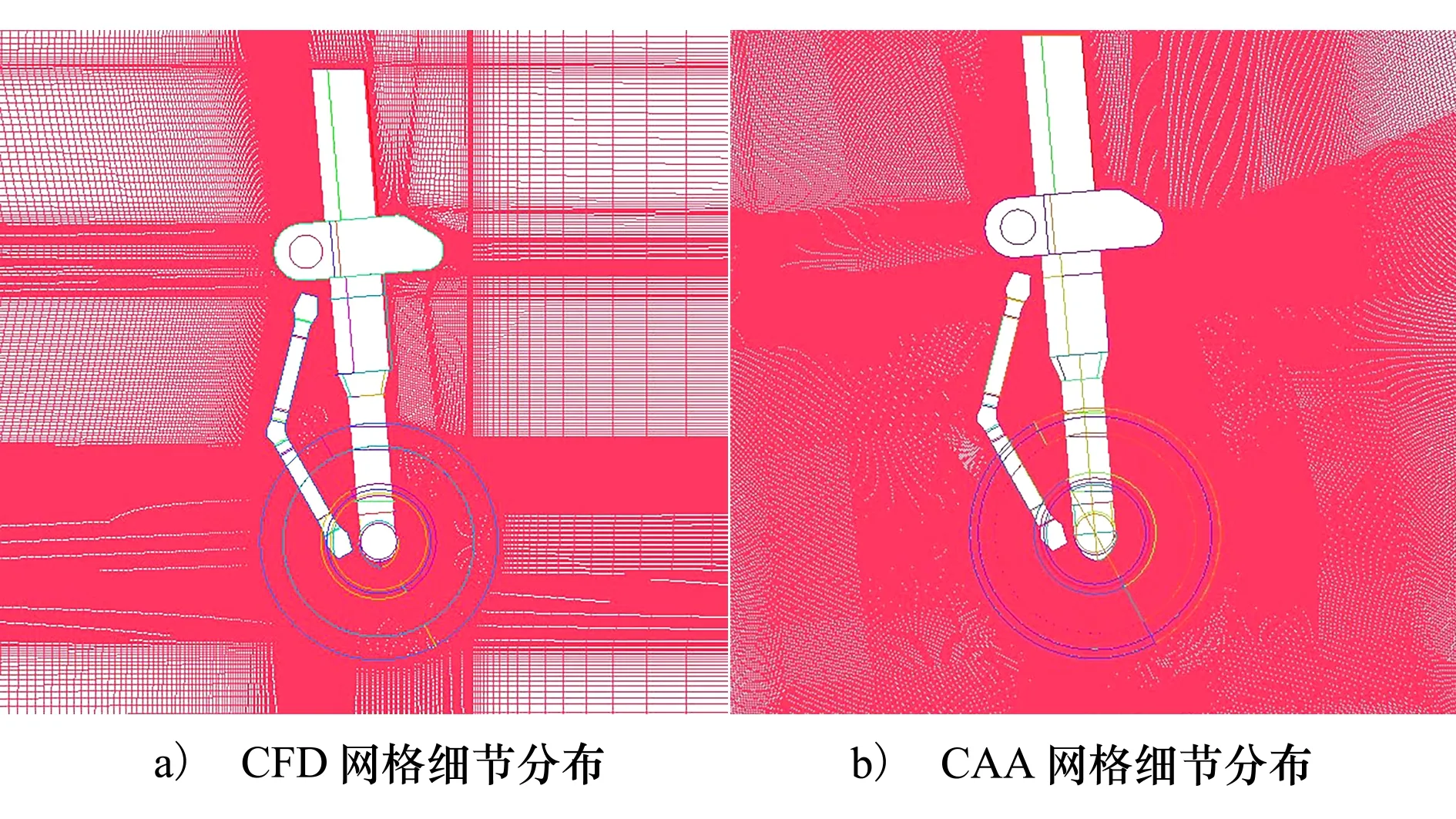
图5 CFD和CAA网格分布

CFD非定常计算的无量纲时间步长为Δt/c=0.01。CFD计算边界条件：物面采用无滑移边界条件；计算域采用无反射边界条件。CAA计算边界条件：物面使用无滑移边界条件，计算域远场采用无反射边界条件。CAA计算时间步长与CFD非定常计算相同。

4 气动特性及噪声特性分析

为了全方位地对比分析起落架气动特性及其噪声性能，下面给出若干静压、脉动压力、麦克风测点的频谱曲线分析。

4.1 气动特性分析

4.1.1 时均流场特性

图6给出了起落架时均下的流向速度分布。图6a)为x-y平面不同剖面(z=-1.9 m；z=-1.65 m；z=-1.25 m；z=-0.9 m)的流向速度分布，从图中可看出：①除了z=-1.65 m剖面存在较为明显的流场不对称现象外(主要与扭力臂几何不对称有关)，其余剖面基本沿y=0平面对称。②起落架机轮中间存在明显的速度加速区域。图6b)为x-z平面不同剖面(y=-0.17 m；y=0.0 m；y=0.17 m)的流向速度分布，从速度分布可看出：①y=-0.17 m剖面和y=0.17 m剖面存在不对称现象(该现象同样与扭力臂的几何不对称密切相关)，以及后方存在一个较为明显的低速区，这是由活塞杆和扭力臂尾迹低速区扩张效应引起的。②在活塞杆、扭力臂尾迹及机轮内凹腔区域存在负速度分布，说明这些区域存在较为明显的分离现象。

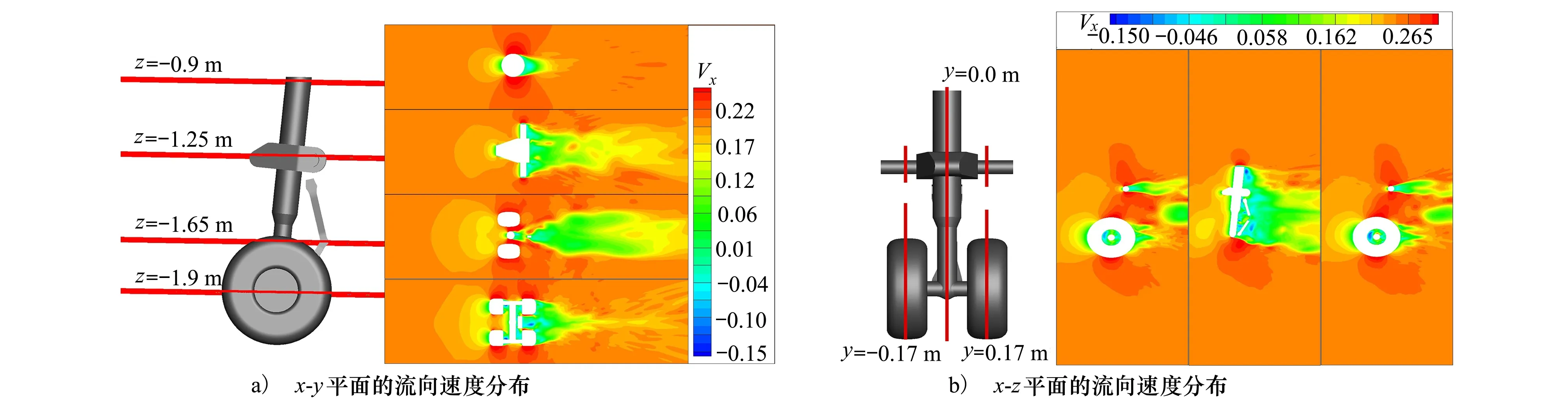
图6 速度分布对比

此外，数值与实验结果均存在静压分布不对称的现象，这主要由两机轮中间的活塞杆和扭力臂阻滞气流所引起。

4.1.2 瞬时流场特性

本节给出起落架构型非定常计算流场的瞬时特征， 图7给出起落架构型Q=-5等值面图，等值面采用流向速度进行着色。在起落架支柱下方轮胎夹缝中、轮胎后缘、横向支杆后缘以及两侧伸出的支杆都脱出了相当丰富的涡系结构，涡管的尺度大小不一。

图7 Q=-5等值面云图(以速度着色)

为了对比分析起落架表面动态压力分布特征，在起落架机轮、机轮凹腔等位置布置了13个脉动压力传感器。图8～10给出了动压传感器在FL-52实验期间测得的壁面压力扰动的功率谱密度(power spectral density,PSD)，以及SST-SAS数值计算的PSD结果。

图8显示了位于左侧机轮中心切面传感器P1～P5的PSD曲线。从0.1～1.8 kHz，实验和数值计算结果有很好的一致性。在频率1.8～5 kHz时，CFD计算结果相比实验结果偏低，这是由于CFD网格的壁面分辨率不足，其理论截止频率约为5 kHz。此外，实验和数值结果均显示P1～P4点在f=560 Hz和f=960 Hz存在2个较为明显的纯音峰值，这与起落架内侧凹腔的流激振荡现象密切相关，并且这2个频率与图9中的P7点的纯音峰值所对应的频率基本一致。然而，P5测点则无明显的纯音峰值，呈现宽频噪声特征，且PSD峰值在整个频率范围均大于P1～P4测点的PSD值。由于该测点处于机轮的脱落涡中，其湍流宽频噪声强度会覆盖了凹腔的纯音强度。

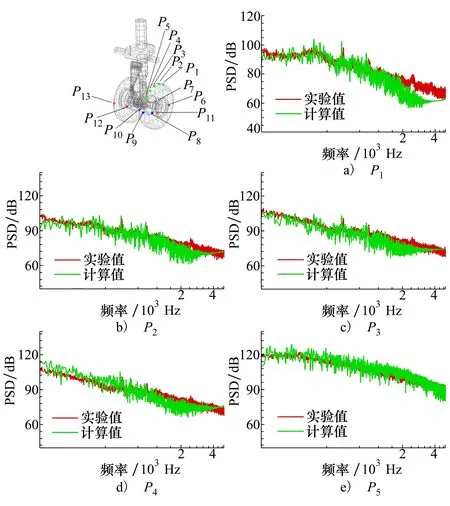
图8 测点P1～P5的功率谱密度曲线

图9为左侧机轮两侧、内侧凹腔及背风区域测点的PSD曲线。其中，P6测点位于左侧机轮外侧凹腔前缘处；P7测点位于机轮内侧凹腔前缘区域；P8～P10测点位于机轮背风区域。从图中可看出：在高频区域(1.8～5 kHz)，P6～P10测点的PSD数值预测误差相比于测点P1～P5更小。在整个频段范围内，数值预测PSD结果与实验结果基本吻合。测点P6主要呈现宽频噪声特性，但实验测试存在一个较弱的f=560 Hz左右的纯音峰值，数值预测结果不明显。对于测点P7，由于处于内侧凹腔前缘，存在明显的2个纯音峰值。位于起落架背风区的P8～P10测点，处于机轮分离区中，呈宽频噪声特性。

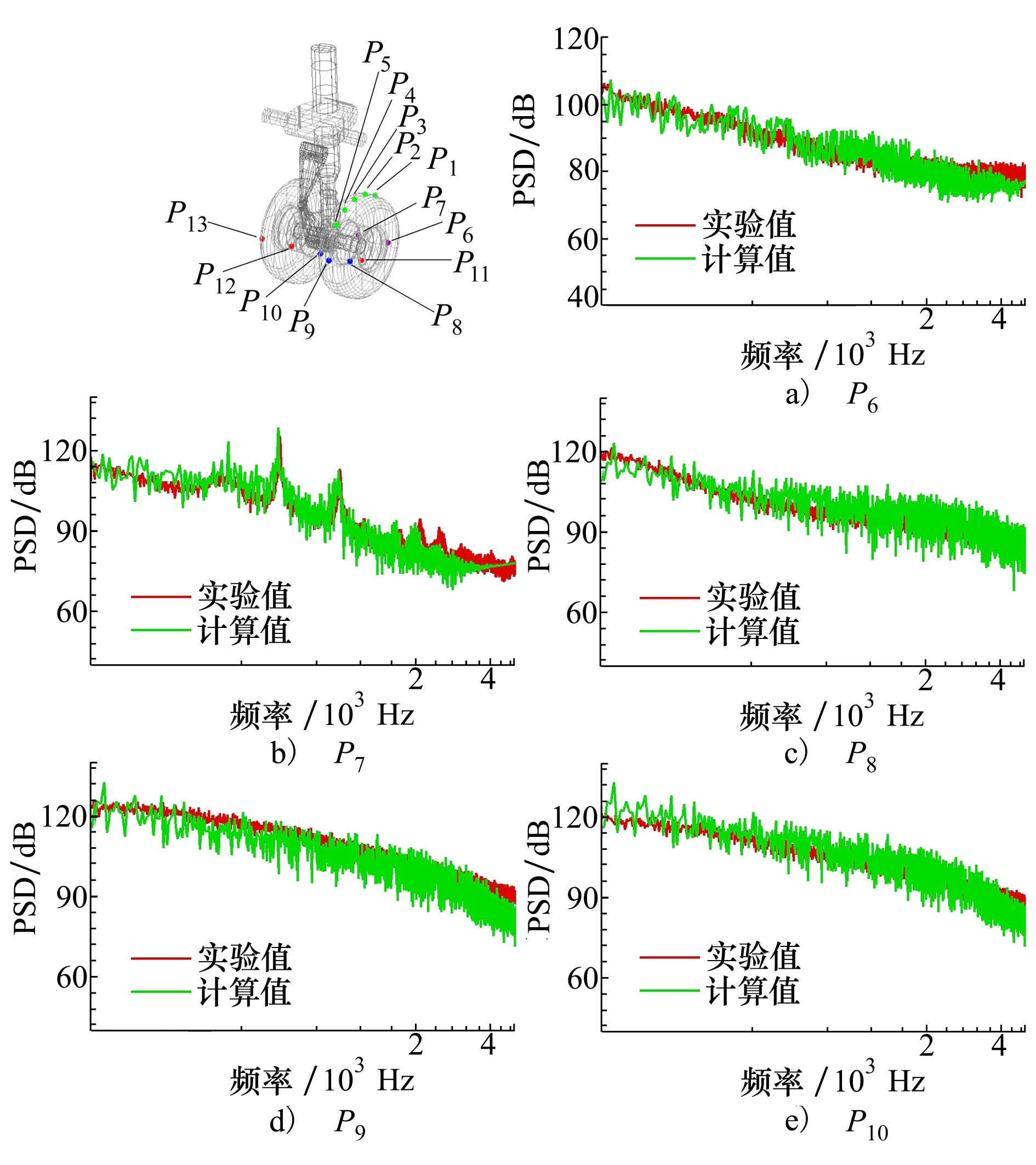
图9 测点P6～P10功率谱密度曲线

图10 测点P11～P13功率谱密度曲线

图10为左侧机轮内侧凹腔底部测点P11、右侧机轮背风区测点P12～P13的PSD曲线。由于受内侧凹腔前缘气流的强烈碰撞，引起反馈回路，形成流激振荡现象，P11测点的PSD曲线存在明显的纯音峰值。而且，位于凹腔后部区域P11测点的PSD峰值强度明显强于测点P7，其最大的PSD峰值达到136 dB。位于左侧机轮P12,P13测点的PSD曲线特性基本与P8,P10相似，呈明显的宽频特性。

4.2 气动噪声特性分析

4.2.1 噪声源分布

为了计算空间场的气动噪声特性，从SAS计算的每一步瞬态流场中提取扰动量，构造APE方程的右端源项。图11为APE方程在某一时刻的声源项分布以及切向图。从图分析可得出：y方向和z方向的声源分布范围相比于x方向更广，且3个方向的声源分布形态与旋涡分布相似。从切面细节可知，声源主要集中在起落架机轮尾迹区、机轮内侧凹腔、横向支撑杆尾迹区、活塞杆和扭力臂尾迹等区域。其中，高频声源主要分布在扭力臂、活塞杆尾迹区域。

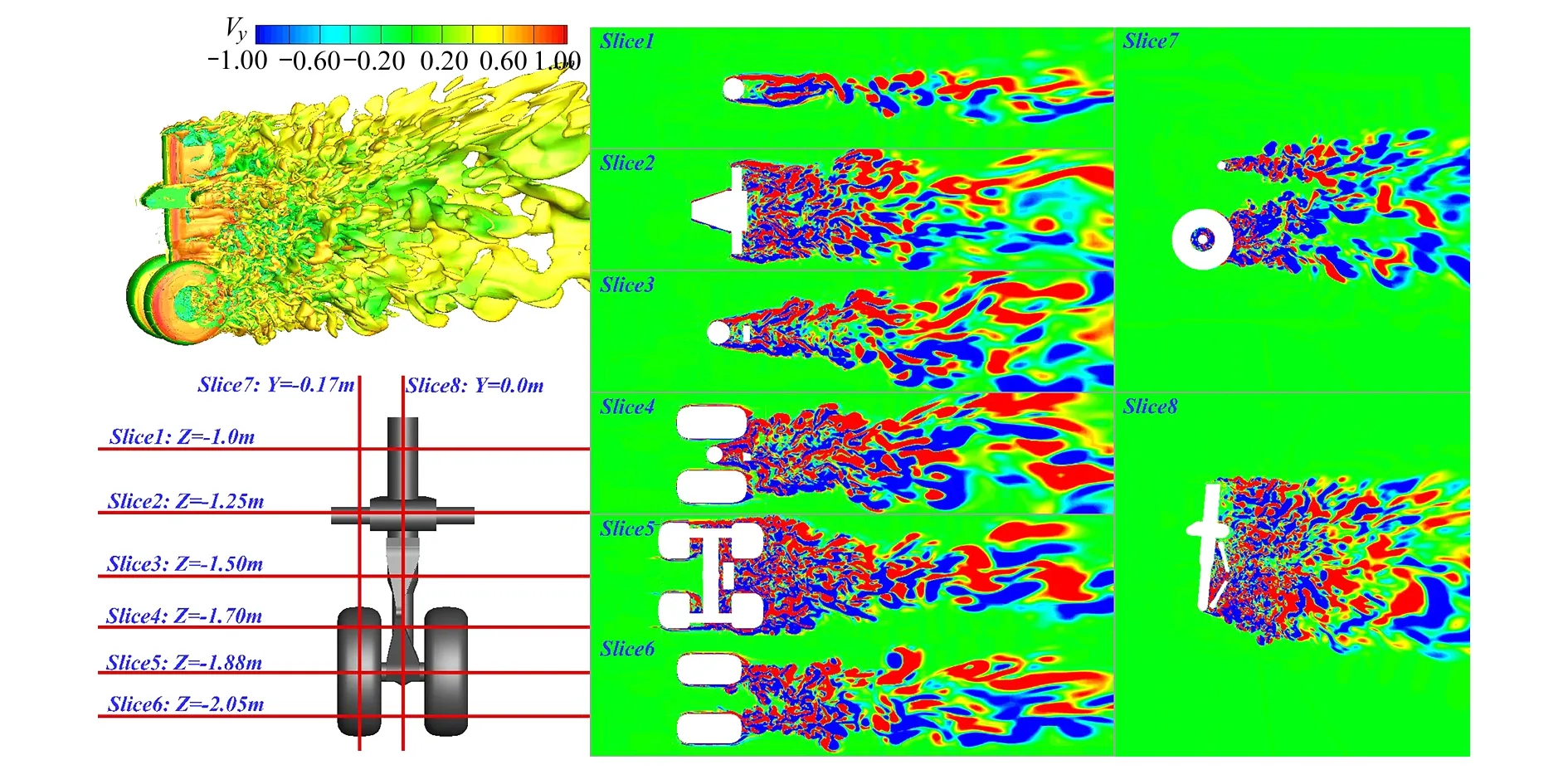
图11 右端源项S2的不同切面图

为了测试起落架表面的声载荷强度，在起落架壁面布置了5个麦克风测点，分别记为M1,M2,M3,M4和M5。其中，M1,M2位于右侧机轮背风区，M3,M4,M5分别位于内侧凹腔底部前、后、中部区域。对比分析图12可得出：①5个测点在2 kHz以内，数值预测结果与实验结果高度吻合，2 kHz以上数值预测结果与实验结果相比偏小。②M1和M2位于机轮尾迹区，其声压级频谱特性呈宽频特征。其中，M1测点在高频区域的声压级幅值相比于M2测点更高，这主要因为M1测点距离扭力臂高频声源区距离更近。③M3,M4,M5在f=560 Hz和f=960 Hz位置处存在明显的纯音噪声，这与动压传感器P11测点的结果基本一致，这些纯音均来自凹腔的流激振荡现象。

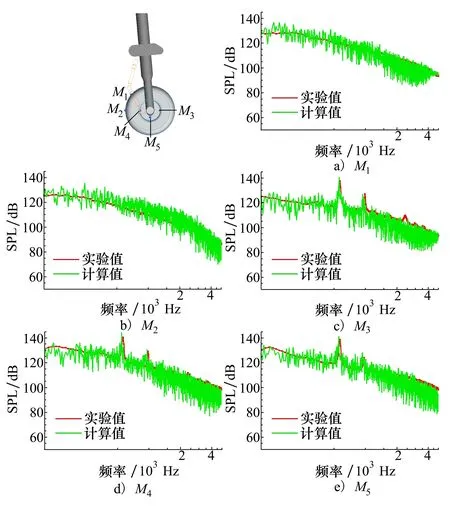
图12 麦克风测点M1～M5声压级频谱曲线

通过上述的脉动压力和壁面声载荷的频谱曲线对比分析结果，可知SAS数值模拟可为声传播方程提供可靠的气动噪声源。

4.2.2 空间声辐射特性

图13为采用APE方程求解获得的某一瞬时时刻的声压分布云图。由于受来流速度的影响，从该图可以很明显地看出起落架前传噪声明显强于后传噪声。为了更准确描述空间的声辐射特性，在实验和数值模拟过程中布置了一组线阵测点，具体如图14所示。该测点距离风洞轴线6.3 m, 角度与来流成50°～130°角，总计17个测点。

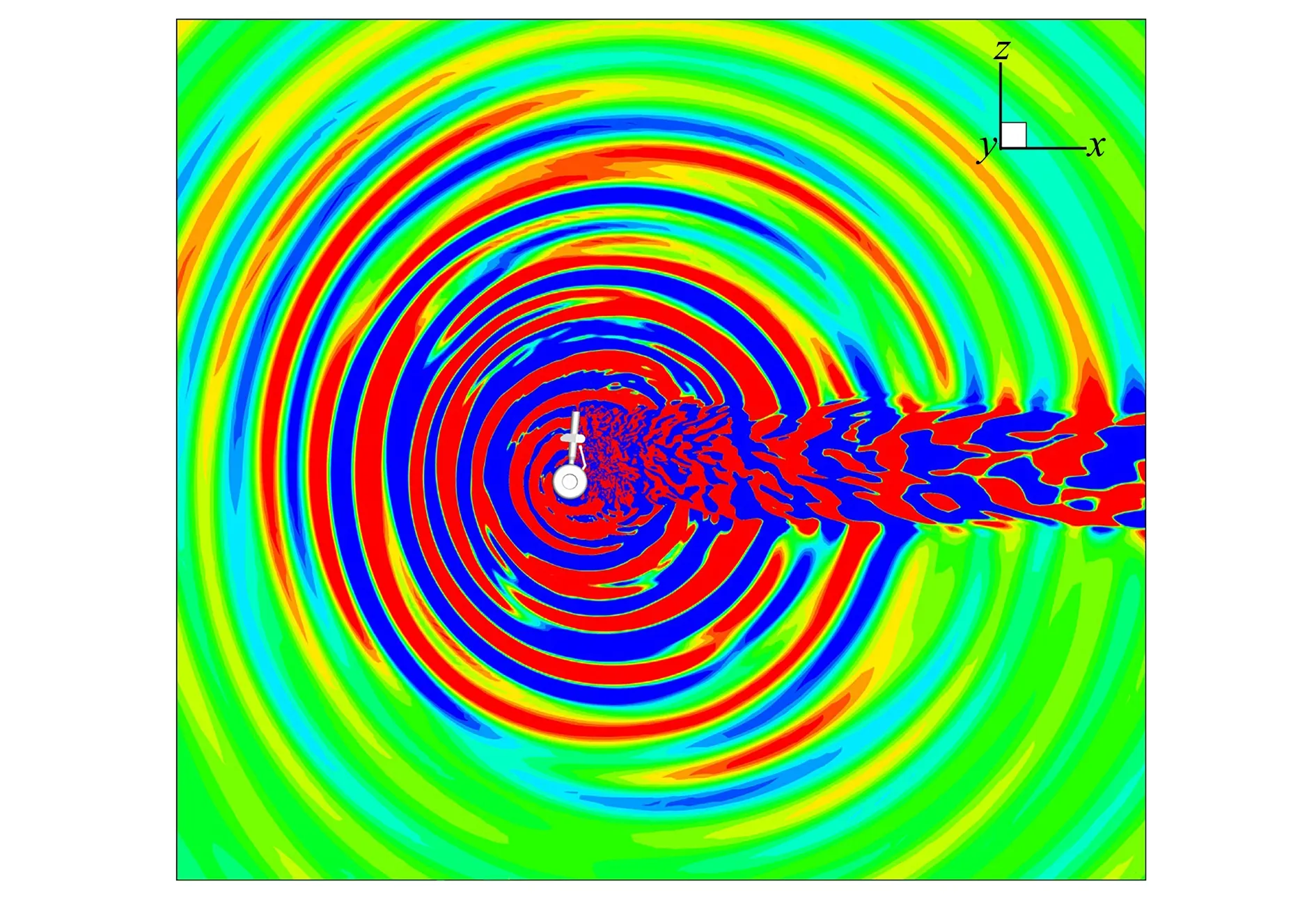
图13 声传播云图

图14 线阵远场测点分布

由于CAA计算网格分辨率的限制，图15给出了在100～3 000 Hz频率范围内，K1,K3,…,K9,K11等6个测点的PSD曲线。其中，红色曲线为实验测试数据，绿色曲线为数值模拟结果。实验测试的PSD曲线和数值模拟的PSD曲线，两者在800 Hz以内的范围内高度吻合。在800 Hz以上的频率范围内，随着频率的升高，PSD误差逐渐增大。从这些监测点PSD曲线可以明显看出，远场噪声基本呈现宽频特性，近场的纯音信号并未传播到远场区域。

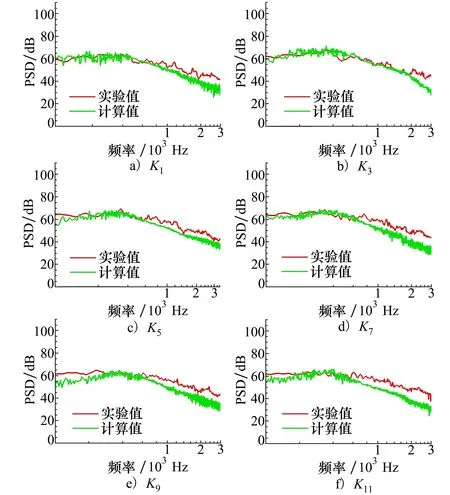
图15 监测点PSD频谱曲线

5 结 论

本文以气动噪声混合预测方法和声学实验技术为手段，开展了全尺寸起落架气动、声学特性分析，具体结论如下：

1) 以声学风洞实验测试数据为基准，验证了SAS/APE气动噪声混合预测方法具备高精度分析起落架气动及声学特性的能力。

2) 根据起落架壁面动压频谱曲线的对比分析可知，起落架机轮内、外侧凹腔存在2个频率(560和960 Hz)的纯音，最大声压级峰值可达136 dB，并且纯音特性可辐射到起落架机轮非分离区域的表面；而位于起落架机轮湍流区域的测点，其壁面压力频谱特性呈宽频特征，未出现纯音特征。

3) 对于本文所研究的起落架，其主要的噪声源分布于起落架机轮尾迹区、机轮凹腔区、横向支杆尾迹区、活塞杆尾迹以及扭力臂尾迹区。而高频的噪声源主要由活塞杆、扭力臂等小尺寸部件引起。

致 谢感谢中航工业第一飞机设计研究院、中航工业空气动力研究院提供的起落架模型及丰富的气动、噪声实验测试数据。