改进搜索者算法在边坡稳定分析中的应用

周亮， 李刚

(湖南大学 土木工程学院， 湖南 长沙 410082)

边坡稳定分析是岩土工程中一个重大而经典的课题，许多学者在该领域提出了较成熟的理论。其中应用最广泛的安全系数评价方法，需要解决两个问题：① 如何定义并计算判断边坡稳定性的评价指标；② 如何快速而准确找到边坡临界滑动面。针对后者，部分学者将数学上最优化理论应用到边坡工程中，如陈祖煜[1]采用单形法和牛顿迭代法；李德林[2]采用非线性规划法等。但在实际工程中，目标函数往往计算十分复杂，无显式表达式，优化变量间约束较多，数学方法对一些较复杂问题存在局限性。随着计算机技术的发展，智能优化算法在边坡临界滑面搜索领域成为热门，蚁群算法、粒子群算法、模拟退火算法等相继引入到边坡工程中，如陈昌富等[3]基于混沌扰动启发式算法分析土坡稳定；杨善统等[4]将变异算子和二次序列规划引入粒子群算法中进行边坡滑面搜索；胡军等[5]利用协调粒子群算法CPSO和BP神经网络对边坡的稳定性进行预测，这些方法均取得了较好的结果。

2006年，戴朝华等[6-8]提出一种新型人工仿生算法——搜索者寻优算法(Seeker Optimization Algorithm,SOA)，该算法与粒子群算法(Particle Swarm Optimization,PSO)原理十分相似，具有构造简单、收敛速度快等优点，但仍存在易陷入局部最优值的问题。

张连强等[9]引入模拟退火算法思想改进SOA算法；屈迟文等[10]对达到某一标准的种群进行动态自适应t分布变异操作；Lin等[11]引入反向学习策略，Guney等[12]提出回溯策略，均对SOA算法进行了一些改进。该文在原始SOA算法基础上，引入混沌策略提出改进搜索者寻优算法(Improved Seeker Optimization Algorithm, ISOA)，进一步结合有限元应力代数和法，分别对多层土边坡、含软弱层土坡进行分析，计算结果显示了该算法的高效性与精确性，适于在工程领域应用。

1 ISOA算法理论

1.1 SOA算法的基本原理

1.1.1 搜索方向

(1)

(2)

(3)

搜索者i最终的移动趋势是以上3个方向的组合，SOA算法中关心的只是方向矢量，因此用符号函数sign()取正负号。

(4)

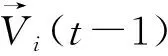
1.1.2 搜索步长

SOA算法采用模糊推理模拟人的智能搜索行为，确定搜索者移动的尺度大小即步长，用高斯隶属函数表示搜索步长与隶属度的关系：

u(α)=exp[-α2/(2δ2)]

(5)

式中：u为隶属度；α为步长；δ为隶属函数参数。

定义个体隶属度与其适应度(即目标函数值)降序排列后的序号成正比。

(6)

uij=random(ui,1),j=1，2,…,D

(7)

式中：Ii为搜索者i按适应度降序排列后对应序号；ui为搜索者i对应函数值的隶属度，uij为其第j维搜索空间目标函数值的隶属度；s为种群规模；设定隶属度的上下限umax=0.95，umin=0.011 1。

由式(5)隶属度反推步长：

(8)

(9)

式中：δij为高斯隶属函数参数；xmax、xmin分别为当前种群中的最大、最小适应度对应的搜索者位置。

1.1.3 更新位置

由式(4)、(8)，更新搜索者i的速度和位置：

Vij(t)=αij(t)dij(t)

(10)

xij(t+1)=xij(t)+Vij(t)

(11)

1.2 引入混沌局部搜索策略的ISOA

SOA算法概念清晰明确，易于编程，且具有收敛速度快、鲁棒性好的优点。然而，在搜索前期个体移动步长大，不能进行局部搜索，后期个体聚集在一起，δij趋于0，步长αij也趋于0，种群停滞不前，为提高算法精度，该文引入混沌策略改进。

混沌是介于完全混乱与有序之间的一种状态，是既定的随机遍历。混沌变量[13]是在一定范围内取得初值后，根据迭代公式得到的一组随机序列，常见的Logistic序列，映射公式为：

Z：zk+1=μzk(1-zk)，k=0,1,…

(12)

式中：Z为混沌变量；zk为Z一次取值；μ为控制参数。

混沌变量具有以下重要性质：

(1) 随机性：混沌变量看似随机，表现出随机特征。

(2) 初值敏感性：初值z0不同，由式(12)产生的混沌序列完全不同。

(3) 有界性：混沌变量的取值是有范围的。

(4) 遍历性：若参数选取合适，混沌变量能取遍其范围内的每一个值且不会重复。

(5) 规律性：混沌变量由确定的迭代公式产生。

对于优化问题minf(x)，混沌算法(Chaos Optimizition)[13]首先将混沌变量Z映射到搜索域(xmin,xmax)内：

(13)

式中:n为x的维数，(xi,min,xi,max)为第i维xi的上下界。

计算f(xk)对xk进行评价，若其结果好于给定初始解x0则接受xk，以xk替代x0，否则令k=k+1，计算下一个点，直到达到一定精度或最大迭代次数。由于混沌变量的遍历性，当k取值次数足够大时，xk(k=1,2,…)在(xmin,xmax)内遍历。

(14)

r=[rmax-(rmax-rmin)t/tmax](bmax-bmin)

(15)

此外，智能群体算法均要求种群初始解尽量分布均匀于其定义域中，考虑到混沌变量的遍历性，可通过混沌序列生成初始种群：

Z0→X0:X0=bmin+(bmax-bmin)Z0

(16)

1.3 ISOA算法流程

ISOA算法流程如图1所示。

图1 ISOA流程图

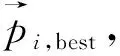
Step2:执行搜索策略，由式(4)、(8)计算个体i在每一维j上的搜索方向αij(t)及前进步长dij(t) (i=1,2,…,s，j=1,2,…,D)。

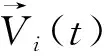
Step5:t=t+1，若t>tmax,停止搜索，输出结果；否则返回Step2。

2 数值仿真试验

为验证ISOA算法在函数优化中的良好性能，该文参考文献[4]、[5]、[15]与[16]选取了表1中7个基准函数分别对ISOA、SOA算法进行测试，其中F1、F2、F3为单峰函数，F4、F5与F6为多峰函数。这7个函数的全局最小值均为0，除F2外极小值点都在x=0处，F2的极小值点x=(1,1,…,1),测试函数维数n=30。

表1 基准测试函数

SOA与ISOA算法参数设置相同，种群规模s=30[7]，最大迭代次数应尽量取较大的值，使迭代最终处于较稳定的状态，可取tmax=1 000，惯性权值ω线性递减(0.9→0.1)，学习因子c1=c2=0.5，ISOA中混沌搜索次数k取30。每个函数用SOA与ISOA两种算法各独立计算30次，统计30次寻优结果的最大值、最小值、均值及标准差记录于表2中。图2为函数某一次计算的优化过程曲线。

从表2中均值一栏看出：ISOA算法的精度是数量级的提升，如函数F1的均值从10-4降到10-40，F6的均值从10-7降到10-15；从标准差一栏看，ISOA算法的稳定性十分良好。从图2可以看出：ISOA算法的优化效率也比SOA高，如函数F2，ISOA约在第200次迭代就已经达到SOA算法约第400次迭代的精度，函数F6，ISOA约在第400次迭代就已经达到SOA算法约第700次迭代的精度，这表明达到相同精度时ISOA算法所需迭代次数更少，因此ISOA寻优效率更高。

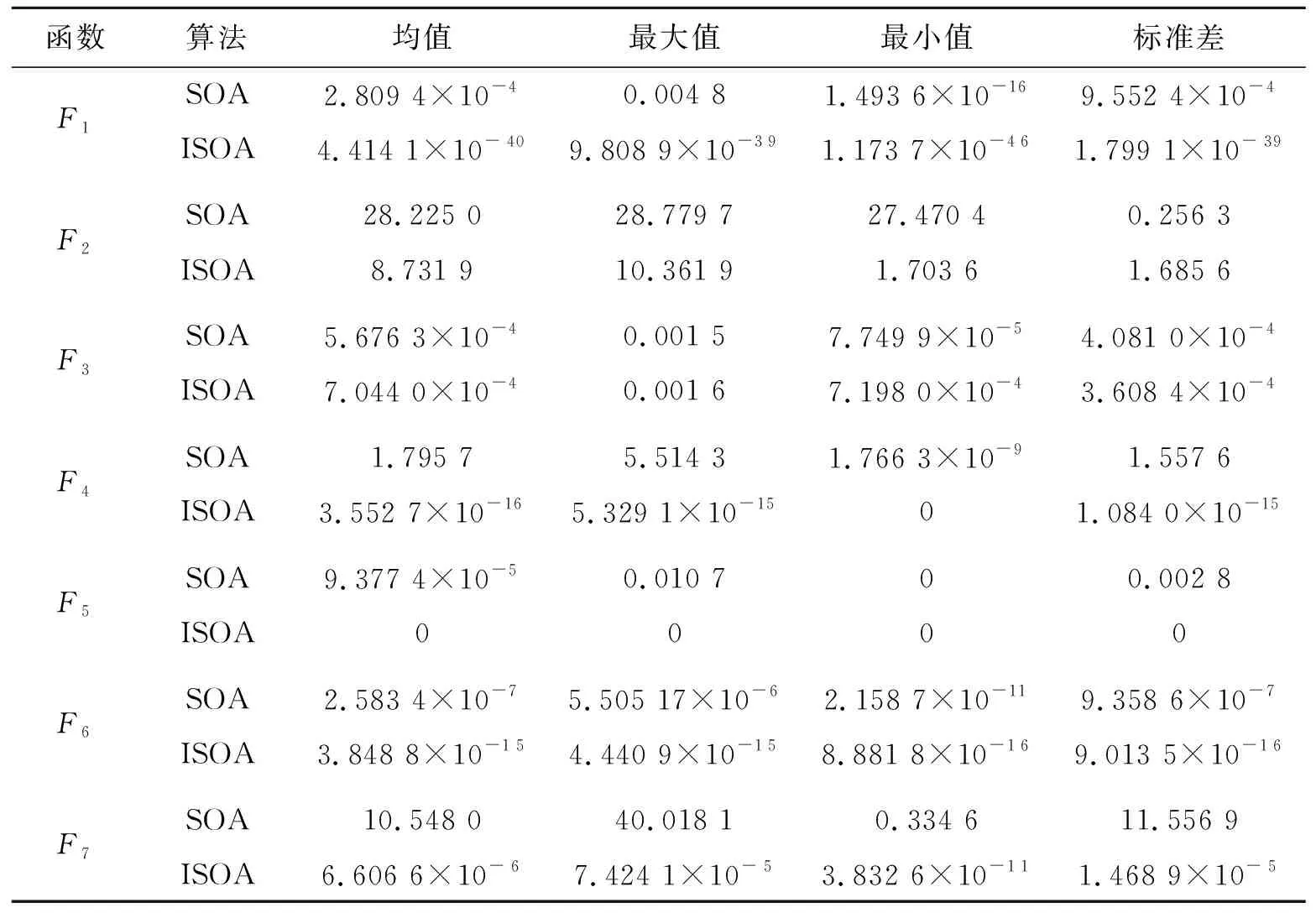
表2 测试函数寻优结果

图2 测试函数优化过程曲线

3 基于ISOA的边坡临界滑面搜索

边坡安全系数求解方法有极限平衡法、有限元强度折减法等。其中有限元应力代数和法[17-18]基于有限元数值计算结果，定义安全系数为抗剪强度τf沿滑裂面l积分与真实剪应力τ沿滑裂面l积分之比，该法满足应力-应变协调关系，相比有限元强度折减法计算简洁，只需进行一次有限元计算，易于编程实现，该文采用有限元应力代数和法计算边坡安全系数：

(17)

式中：l为某一滑裂面曲线；τ、τf为滑裂面上一点沿切向方向的剪应力与抗剪强度；σn为该点滑裂面法向的正应力；c、φ为土层黏聚力与内摩擦角。

式(17)直接积分困难，一般采用分段求和计算。

将曲线滑裂面l近似离散为n个控制点连成的折线(图3、4)，则边坡临界滑裂面的搜索即为函数Fs=f(x1,y1,x2,y2,…,xn,yn)寻优问题。直接以控制点的坐标(x1,y1,x2,y2,…,xn,yn)作为优化变量，自由度有2n个，同时在搜索过程中会产生大量无效的滑裂面，会降低搜索效率，若x1、x2、…、xn间距相等，y1、yn由坡面函数确定，优化变量为(x1,xn,y2,y3,…,yn-1)，自由度只有n个。

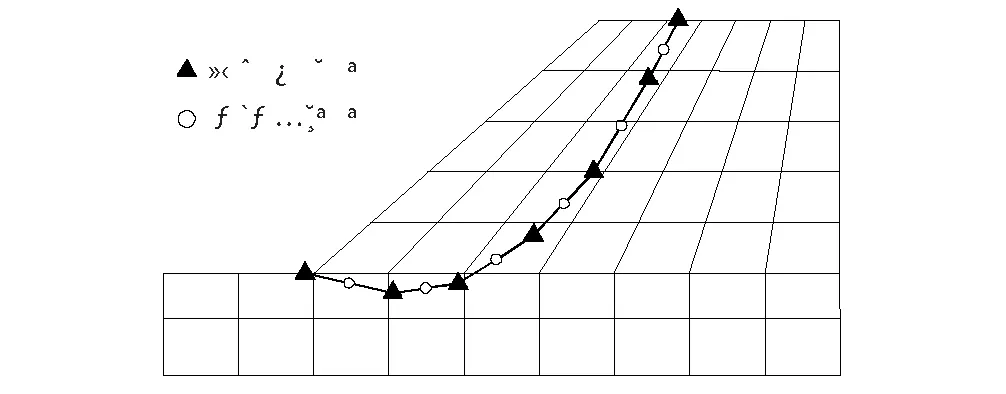
图3 应力代数和法计算安全系数

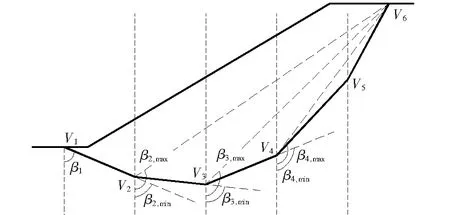
图4 滑裂面示意图

以坡角为原点，水平向为横轴，竖向为纵轴建立直角坐标系，有：

(18)

可以看出yi与βi-1(i=2,3,…,n-1)是一一对应的关系，故该滑裂面也可用n个变量(x1,xn,β1,β2,…,βn-2)唯一描述,且各变量间存在如下约束：

x1,min≤x1≤x1,max

xn,min≤xn≤xn,max

β1,min≤β1≤β1,max

βi,min≤βi≤βi,max,i=1,2,…,n-2

(19)

式中：[x1,min,x1,max]为滑出点范围，[xn,min,xn,max]为滑入点范围，[β1,min,β1,max]为滑出角范围，均为给定条件，且：

(i=2,3,…,n-2)

问题即转化为函数Fs=f(x1,xn,β1,β2,…,βn-2)带约束式(19)的寻优计算。

4 算例分析

为验证ISOA算法在边坡工程中的适用性，将 ISOA算法运用到边坡临界滑裂面搜索中。通过两道澳大利亚计算机协会(ACADS)考核题[1]，对比ISOA与SOA两种算法的计算过程与结果。有限元计算采用Abaqus软件，其中土体采用理想弹塑性本构模型、摩尔库仑屈服准则和非关联流动法则，模型边界条件为底部固定，两边水平方向固定。利用Matlab程序提取有限元计算结果，采用自编Matlab程序搜索边坡临界滑裂面。SOA与ISOA算法参数设置相同，种群规模s=25，最大迭代次数tmax=400，惯性权值ω线性递减(0.9→0.1)，学习因子c1=c2=0.5, ISOA中混沌搜索次数k取20。

算例1为多层土坡，安全系数推荐为1.39，滑出点x1范围为[11,15.5]，滑入点xn范围为[34.5,40]，滑出角β1范围为[30°,90°]，滑面控制点10个；算例2为含软弱层土坡，地下水位位于软弱层底部，地下水位以上孔压为零，安全系数推荐为1.26，滑出点x1范围为[17,23.5]，滑入点xn范围为[47.5,54]，滑出角β1范围为[20°,90°]，滑面控制点12个。边坡材料参数及几何模型见表3与图5。

表3 ACADS考核题1(c)与3(a)土层参数

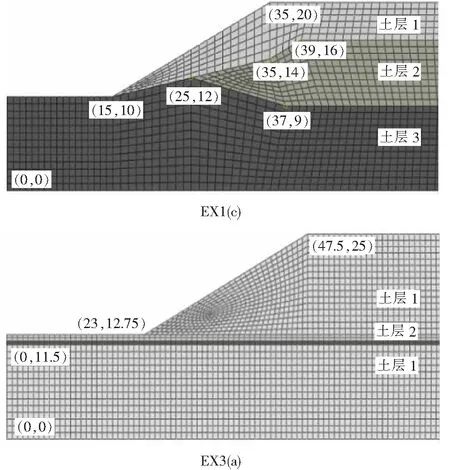
图5 ACADS考核题EX1(c)与EX3(a)

表4记录了各种方法计算安全系数结果，图6为两种算法(SOA、ISOA)搜索的临界滑裂面。

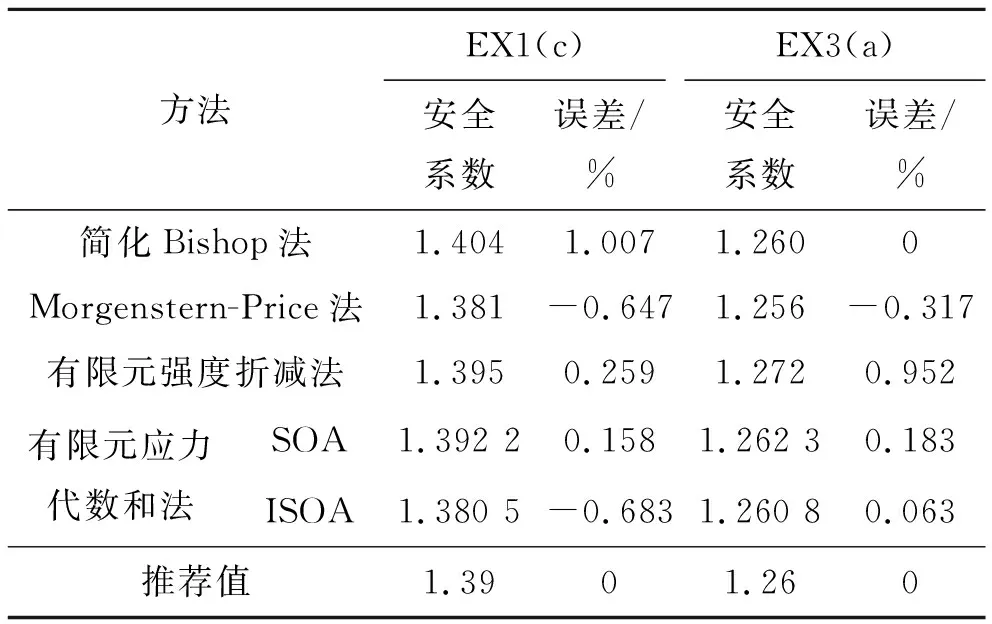
表4 EX1(c)与EX3(a)计算结果

从表4可以看出：在非均匀土坡中，各类极限平衡条分法的结果差异较大，相比之下有限元法计算的结果更可靠，安全系数误差在1%以内；其中两种寻优算法得到的安全系数和临界滑裂面位置均与极限平衡法的结果基本一致，且EX3(a)均通过了软弱夹层。图7为两种算法中安全系数迭代过程曲线，从安全系数效果看，由于采用的安全系数计算方法、滑面形式等不同，该文的两种算法结果与参考值存在误差但不大，均达到了理想的结果，若从求最小值效果来看，ISOA算法的结果要优于SOA算法，且达到相同精度时ISO算法所需迭代次数更少，搜索效率更高。

图6 临界滑动面比较

图7 安全系数迭代过程曲线

5 结论

该文基于改进搜索者寻优算法寻找边坡临界滑动面，并结合有限元应力代数和法分析边坡稳定性，得出如下结论：

(1) 基于ISOA的有限元应力代数和法与极限平衡法的计算安全系数误差较小，临界滑动面位置基本一致。有限元应力代数和法中安全系数无具体表达式，计算量大，且边坡工程中优化变量约束多，一般的优化方法不适用，智能优化方法则能很好地适应，因此将有限元计算结果与智能优化方法结合分析边坡稳定是可行的。

(2) 将混沌算法与SOA算法结合，可以克服单一算法的局限，ISOA精度、稳定性和效率都有极大的提高。ISOA算法在非均匀和含软弱层土坡临界滑面搜索中均取得了较好的结果，该算法非常适合于隐式目标函数，优化变量间相互关联、约束较多等状况的寻优计算，未来在工程领域优化分析中的应用前景将十分广阔。