一道恒成立求参数取值范围问题的解法探究

山西省太原市第三实验中学校 (030031) 董立伟

恒成立求参数取值范围问题是导数解答题中一类重要的也是常见的题型.这类题型将函数、导数、不等式等知识，函数与方程思想、数形结合思想、分类讨论思想、转化与化归思想等数学思想有机融合，知识背景丰富、呈现形式多样、思维层次较高、解题方法灵活，能有效考查学生的应变能力、对知识和方法的综合应用能力，及逻辑推理、直观想象、数学运算等素养.

一、试题呈现

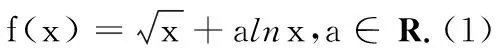
试题第(1)问是常规的含参函数单调性问题，利用分类讨论法可以轻松解决，本文不再赘述.第(2)问以恒成立问题为情境，又隐含了Karamata不等式的背景，使得试题的解法灵活多样，有利于不同思维水平的学生作答.

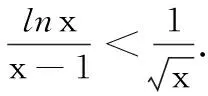
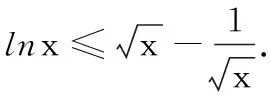
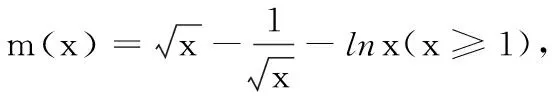
二、解法探究

视角一：分类讨论

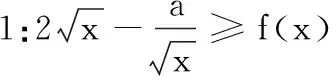
点评：解法1将原问题等价转化为“函数g(t)≥0在区间[1,+∞)上恒成立”，之后以函数g(t)的导函数g′(t)的判别式4a2-4a在区间[1,+∞)上的正负为依据确定分类讨论的标准，并在每种情况下分别确定使得问题恒成立的参数a的取值范围，求解问题.

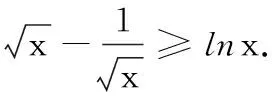
从更大视野来看，赛努奇对中国绘画的关注是从对整个中国文化关注的角度切入的，是对中国历史、生活等方面的兴趣在引导其对绘画的购藏。赛努奇对中国绘画的收藏是从文化的广阔视野下对中国绘画进行观照和思考认识，而不是从所谓的于历史中建构起来的“审美”角度来进行判断和选择。赛努奇以西方文化的“他者”之眼，从中国绘画历史和理论相对狭隘的束缚中逃脱出来，而向我们展示了更为丰富、充盈的中国传统美术样态。这与当时法国汉学家、收藏家对中国绘画之于中国历史、文化的关系所持有的重视态度、进行研究和收藏属同一流向，也即赛努奇博物馆的人物画收藏对整个欧洲关于中国绘画和文化的理解，具有样本性的代表意义。

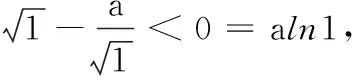
综上，a的取值范围是(-∞,1].

点评：当a=1时，原问题恰好退化为引理.因此，解法2以引理所述不等式为依据，确定分类讨论的标准：“a=1”、“a<1”和“a>1”，并借助于放缩法及取特值的方法确定参数a的取值范围.

视角二：分离参数

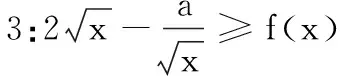
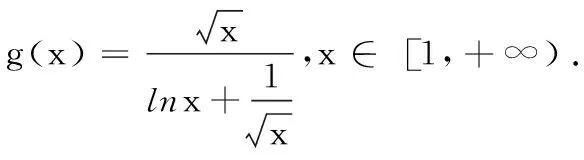
点评：解法3采用分离参数法，将原问题转化为a≤g(x)min的问题，之后利用多次求导的方法确定g(x)的最小值，解决问题.

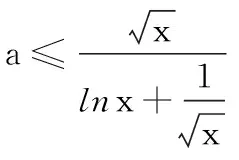
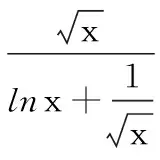
视角三：寻找充分必要条件

解法5：同解法2，对任意的x∈[1,+∞)，①式恒成立.可知，“x=1时①式成立”是“对任意的x∈[1,+∞)，①式恒成立”的一个必要条件.将x=1代入①式得1-a≥0，解得a≤1.

下面证明“a≤1”是“对任意的x∈[1,+∞)，①式恒成立”的一个充分条件.

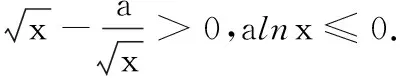
所以，a的取值范围是(-∞,1].

点评：解法5以“x=1时原问题成立”为突破口，找到原问题的一个必要条件“a≤1”，再证明“a≤1”也是原问题成立的一个充分条件，解决问题.