以少促多求发展 角色转换促提升

江苏省苏州实验中学 (215000) 丁先宝

众所周知，成功的教学并不是看教师讲了多少知识，学生做了多少道题，而是看教学过程是否调动了学生的学习积极性，是否让全员都获得了提升.现行教学中，部分教师常常会担心学生学不会，为此对一些教学重难点内容常常反复讲，重复讲，然讲得越多，学生思考的就会越少，这样真正理解和掌握的知识也就很有限，久而久之在学习中容易出现“懂而不会”的现象，教学效果难以达到预期.为了改变这一现象，教师应少一点担心，多一些信任；少讲一些内容，多一些鼓励和引导；少一些直接灌输，多一些主动建构，从而借助“少”让学生收获“多”，进而积聚能量，厚积薄发.

一、少讲多听，引导学生主动思考

在数学教学中，部分教师为了追求效率，常将自己的解题思路和解题经验强加给学生，这样使学生的“学”变得消极、被动，影响教学效率.

为了节省教学时间，让学生少走弯路，教师给出题目的同时也给出了如下两个提示：

(1)常规解法：重复两次“移项、平方、整理”可以去除根号，完成化简，但是该方法运算量较大.

(2)定义法：仔细观察容易发现它与双曲线的定义密切相关，在解题时可以借助定义来解题.

有了以上的提示，学生豁然开朗，在教师的带领下直接应用双曲线第一定义顺利地完成了题目.至此该问题探究结束，教师又开始讲解下一个问题.

从上面过程容易发现，学生的思路跟着教师走，虽然能够顺利求解，但是缺乏主动思考和主动建构的过程，学生难以对问题形成更深层的认识，不利于解题能力提升.其实，在解题时，不应急于给出引导或给出答案，而是应放手让学生去独立探究，哪怕在探究过程中会碰壁，哪怕最终不能顺利求解，但是学生参与其中必然会有所收获.试想，若教学中学生还没有来得及审题，教师就给出了答案，这样学生只能机械地将解题过程记录下来，课下再进行进一步的理解和消化，这样不仅会增加学生的课业负担，而且容易让学生产生厌烦情绪，影响教学实际效果.要知道，学生学习的过程应该是一个自主建构的过程，若试图用教师的“讲”来替代学生的“学”，一定是徒劳的.

以上现象在课堂上较为普遍，其实有时候教师可以尝试放手，退居二线，让学生从自己的已有知识和经验出发，多思考，多操作，往往可以收获意外的惊喜.

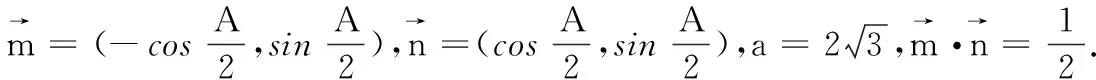
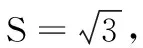
(2)求b+c的取值范围.

通过交流发现，之所以出现不同的结果，是因为生1在解题是忽视了“两边之和大于第三边”这一限定条件，将条件补充完整亦可以求解.

从以上求解过程可以看出，不同的学生对知识点的理解和掌握程度不同，为此在解题时其出发点也会有所不同，这样在解题时以学生为主体，让学生交流展示，有效地帮助学生摆脱了思维定势的束缚，提升了解题效率.同时大家相互沟通，相互纠错，可有效避免学生“一错再错”，有利于提升解题准确率.

二、少讲多问，诱发学生主动建构

学习过程也是一个解决问题的过程，为了让学生学会学习，首先要让学生学会提问，注重培养学生问题意识.同时，学生在解决问题的过程中也要发挥评价的引导和激励作用，通过交流、评价引导学生抓住问题的本质，培养思维的多样性和深刻性，有效提升学习主动性，提高教学效率.

案例3 抛物线y2=4x与直线y=x-1相交于A、B两点，求线段AB的长.

教师预留5分钟让学生独立思考，接下来通过师生交流共同完成.

师：说一说你是怎么解的？

生1：将两方程联立，可求得A、B两点的坐标，结合两点距离公式，求得线段AB=8.(从学生反馈来看，大多学生都应用该方法)

生2：我也是利用了方程的思想，消去y得x2-6x+1=0，但是我没有求A、B两点的坐标.(学生投来诧异的眼神)

师：说一说你的想法.

生2：设A(x1,y1)，B(x2,y2)，AB=

生3：抛物线y2=4x的焦点坐标为(1,0)，正好在直线y=x-1上，设A(x1,y1)，B(x2,y2)，利用抛物线定义可知，AB=x1+x2+p，而x1+x2=6，故解得AB=8.

师：大家都说得非常好，利用不同的方法最终求得了答案，你们评价一下哪个解法更简单呢？

生4：生3利用定义来求解最简单，不仅有效地规避解方程组的繁琐运算，而且在应用根与系数关系时也不需要为了求(x1-x2)2而配方.

师：说得很好.不过本题存在一定的特殊性，即抛物线的焦点正好在直线上，若把直线改为y=x+1，是否还能按照生3的思路求解呢？

生齐声答：不能.

师：确实，应用定义是有条件的.那么你们评价一下，生1和生2两种解法有什么区别和联系？

生5：生1和生2的解题都是先消元，生1是要求出y，而生2是借助整体代入，不需要求出y，利用根与系数关系即可求解.

师：大家仔细分析上面三种解法，看看他们有什么共同之处？

生6：其实都是解方程组.

师：现在大家一起来分析一下三种方法的优缺.

生7：生1的方法比较通俗易懂，在解题时较为常用，不过若交点坐标比较简单的话这个方法比较方便、快捷，否则运算会比较繁琐.

生8：利用定义来求弦长虽然简单，但不是很通用.

生9：借助根与系数关系虽然变形时略显繁琐，不过可以有效规避复杂运算，是求弦长的一般方法.

师：是的，有的方法思路简单却运算复杂，复杂运算不仅有错解风险而且比较消耗时间，为此在解题时尽量将问题向简单化转化，以此提高解题效率.

以上教学过程中，教师将舞台交给了学生，学生以“主角”的身份自由地发挥和展示，有效地激发了学生的主动性和创造性.同时教师又将评价的机会交给了学生，让学生在解题的基础上思考其他解法的优劣，从而进一步加深对问题的理解，不仅抓住了问题的本质属性，也总结归纳出了一类题的通性通法，让学生对消元、转化等数学思想有了更深层的认识，较好地优化了学生的认知结构.

三、少讲多思，引导学生解后反思

大多学生谈起数学学习都感叹于“题海无边”，尤其在高三复习阶段更是感觉有刷不完的题，考不完的试.“做”占用了学生大多的时间，学生很少有时间进行解后反思，进而忽视了数学思想方法的总结和提炼，忽视了解题中对错因的分析和总结，从而使得学生对问题的理解不深，在解题时经常会出现“一错再错”的现象.为此，在数学教学中，教师应引导在课后做好总结归纳，要让学生知道自己收获了哪些，还有哪些不足，还有哪些知识需要巩固，进而便于学生更好地认识自己，认识数学.

例如，在考试结束后，教师可以让学生撰写考后反思，把自己成功的经验，存在的问题及解决策略都一一的撰写出来，让学生对这次考试及近期的学习状态有个全面的、清晰的认识，从而采取有效的有段进行及时地修补，如若运算失误多，那么就在算理和算法上进行强化；若感觉解题速度慢，那么平时作业和练习时可以采用计时法来提升解题注意力，提高解题效率；若方法应有不当，可以反思是哪个知识点理解不清造成的，等等，从而通过改善不足来提升学生成绩.

总之，在数学教学教师要尽量地“少”讲一些，为学生营造一个展示和发展的空间，这样才能将学生培养成为个性张扬的、懂合作、会创新的新型人才.