灵活编组高铁列车的售票时间窗优化

闫振英，韩宝明，李晓娟，曹瑾鑫

(1.内蒙古大学 交通学院，内蒙古 呼和浩特 010020；2.北京交通大学 交通运输学院，北京 100044；3.内蒙古自治区科学技术研究院，内蒙古 呼和浩特 010070)

2019年以来，我国铁路部门积极探索构建灵活的高铁票价机制，研究并试点“一日一价”、“一车一价”等策略.高铁收益管理理论研究早在高铁定价权下放后便受到广泛关注.在票额分配、动态定价及二者联合优化等方面取得了一系列研究成果，促进高铁运营管理效率的提升，助力高铁运营市场化改革.随着动车组技术的发展，我国研发出的新型CRH3X型动车组可实现2～16编灵活编组[1].灵活编组技术可用于调节供给容量，打破了传统收益管理容量固定的限制，灵活编组下的高铁收益管理理论和方法亟须探索和研究.

收益管理的研究始于美国航空领域，后广泛应用于各类易逝产品领域.相较于早期研究只考虑单一资源、假设产品需求独立等特征，最新的收益管理研究更多集中在考虑旅客选择行为的网络收益管理上.Strauss等[2]总结了近十几年基于选择的收益管理理论和方法，基于顾客选择的网络收益管理问题可建立动态规划模型精确描述，但是问题规模庞大无法精确求解，于是衍生出诸多获取近似控制策略的研究.许多研究采用MNL(multiominal logit)模型刻画旅客选择行为，得到较为高效的近似控制策略.然而，收益管理中常出现产品不完全独立的情形，MNL模型的IIA(independent of irrelevant alternatives)特性会带来估计偏差[3].随着偏好序模型研究的推进[4]，这种无参数的选择行为模型逐渐应用于收益管理[5].Hosseinalifam等[5-6]提出了基于偏好序选择模型的网络存量控制和预订限制控制策略，并设计了列生成求解算法.Paul等[7]利用树结构研究了基于偏好序的品类优化和定价问题，提出了多项式时间算法.Barbier等[8]针对基于偏好序的网络收益管理问题，从静态近似的角度提出了产品停售控制策略.以上研究都在固定容量的前提下研究收益提升的方法.而Wang等[9]基于飞机机型调换思想为容量提供了部分柔性，研究发现机型调换与存量控制联合优化能够提升收益.综上，理论探索中尚缺乏有限柔性容量下考虑偏好序选择行为的收益管理研究.

既有高铁收益管理研究成果主要集中在票额分配[10-11]、动态定价[12]、动态定价与票额分配联合优化[13]等方面.票额分配一般预先确定客票价格，通过票额分配模型计算各列车的席位资源如何分配给不同OD(origin to destination)不同票价等级的客票，使得收益最大.动态定价则是通过为客票实时或分时段定价进行预售控制.将实时或时段票价作为决策变量，通过建立票价与需求的弹性关系求解模型.动态定价与票额分配的联合优化则是将票额分配与票价同时作为变量进行求解，得到各时段的最优票价和票额分配方案.此外，Yan等[14]基于灵活编组研究了有限柔性容量下的高铁票额分配问题.以上研究均考虑旅客选择行为，但大多是基于MNL模型，较少采用偏好序模型.

本文采用偏好序模型刻画旅客选择行为，旅客根据自己的偏好集合选择购票，规避MNL模型的IIA问题.基于偏好序的无参数选择行为，由大量历史购买数据驱动，能够更准确表达旅客选择行为，且不假定任何概率形式，具有更好的灵活性和动态性.利用灵活编组对供给容量进行有限调节，各列车容量的增减在一定约束下进行.在此基础上，基于售票时间窗控制策略对高铁收益管理展开研究.针对多列车、多停站的高铁网络，考虑每列车每个OD的相同类型座位提供不同票价的客票，建立非线性规划模型同时优化各类客票的售票时间窗和列车编组方案，从而实现更为精准的供需匹配，提高高铁线路总体获利效果.考虑运营企业的售票要求可将客票进行排序，据此可将模型转化为线性规划模型，并采用CPLEX快速求解.结果可为客票预售提供时间窗控制策略，还可从匹配需求和最大化获利的角度为列车编组计划提供编组规模依据.

1 基于偏好序的灵活编组高铁列车售票时间窗优化模型

1.1 问题描述

一条高铁线路上设有G个车站，开行B列列车服务于沿线的W个OD市场.根据收益管理原理，可以将相同列车、相同等级座位、服务于相同OD的客票设置不同的价格f.列车用b表示，OD用w表示，最终形成的客票可以用唯一标识.依次将客票编号，用j表示，j∈J.不考虑超售和无座票，且假设所有客票停售后不再开启销售.将每列车在每个区段的席位资源定义为资源i∈I.那么客票与席位资源之间的占用关系可表示为矩阵A=[aij]i∈I,j∈J，当产品j占用席位资源i时aij=1，否则aij=0.资源容量ci由列车编组方案zb和额定座位数c0决定.在此仅考虑同等级座位(如二等座)，增加其他等级的座位相当于增加资源类型.将客票销售期划分为τ个时段，从t=0开始，到时段t=τ结束时售票结束.每个产品的售票时间窗由停售时间决定.由于旅客的购票选择行为存在差异，将具有相似购票决策行为的旅客归为一类，旅客类别l∈L.每个时段的旅客类别l的平均到达率为λl.铁路运营企业需要决策每个产品j的停售时间和每列车的最佳编组方案使得整体获利最大.

1.2 基于偏好序的选择行为

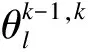
(1)

否则Pl(j|S)=0.因此，将l类别旅客购买客票j的概率表示为Pl(j|{j}).

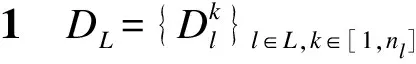
(2)

(3)

1.3 售票时间窗优化模型

客票j的期望销售量Q(DL)可表示为

(4)

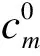
(5)

s.t.公式(3)；

AQ(DL)≤c；

(6)

(7)

∀g∈[1,G-1],∀b∈[1,B]；

(8)

(9)

Tj∈[0,τ],∀j∈J；

(10)

zb，m∈{0,1},∀b∈[1,B],m∈M.

(11)

其中：约束条件(3)表示l类旅客可购买第k个客票的时段，即前k个客票的最晚停售时间超过前k-1个客票最晚停售时间的部分；约束条件(6)为容量约束，总售票数量不应超过列车容量；约束条件(7)为前k个客票中的最晚停售时间的计算方式；约束条件(8)给出了资源容量与列车编组数量和额定席位数的关系，其中g表示区段；约束条件(9)保证每列车只有且只有一种编组方案.约束条件(10)和(11)给出了决策变量的取值范围.根据模型非线性规划的特征，引入客票排序将约束(7)线性化，从而将模型转化为线性规划模型进行求解.

2 模型求解

2.1 客票排序

高价产品和低价产品的嵌套控制是收益管理中非常有效的一种控制方式.例如在存量控制中允许高价产品占用分配给低价产品的资源，从而为高价产品保留更多的售出机会，提高总体收益.铁路运输领域常常存在保护长途客票的嵌套机制.在停售时间控制中，可以用客票停售时间排序来满足嵌套销售的需求.定义客票排序H={Hj}j∈J，如果Tu>Tv，那么Hu>Hv，且若Tu=Tv，则Hu=Hv.一般来说，可按照客票价格、价格除以资源数、单位里程价格等排序，也可以按照运营公司的特殊需要进行排序.

2.2 模型转化

当给定排序H时，模型TC中的非线性约束条件(7)可以转化为

(12)

(13)

s.t.式(3)，式(6)，式(8)～式(12).

转化后的模型TCL为线性规划模型，可选用CPLEX求解器快速求解.得到的模型最优解T*和z*分别为各客票的停售时间和各列车的最佳编组.前者可直接植入售票系统作为售票控制策略使用，后者可为列车编组计划提供参考依据.该模型为静态决策模型，可在售票开始前且编组方案可调整时优化决策.也可在售票过程中且编组方案可调整时重新优化以实现动态决策.

3 数值实验

3.1 实验数据

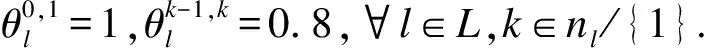
表1 客票与票价

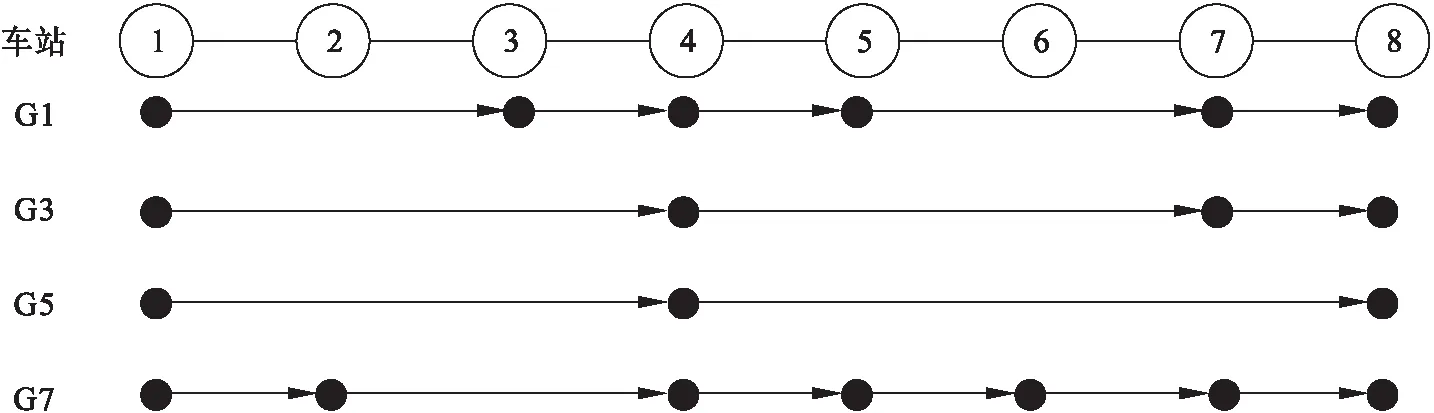
图1 列车服务网络示意图

表2 各OD旅客类别、平均到达率和偏好产品集合

3.2 实验结果

按照上述参数设置，采用CPLEX在处理器为Intel(R)Core(TM)i5-6500 CPU 3.20 GHz，内存4 GB的台式电脑上进行求解.所得最优解为各类客票停售时间(如表3所示)和编组方案(如表4所示)，最优目标函数值(简写为VOF)为1 920 582元，求解时间为0.034 s.计算复杂性能够满足实际应用的需要.

表3 客票停售时间

将8编固定编组(简写为G-8)和16编固定编组(简写为G-16)作为对比方案，本文提出的灵活编组方案用G-F代表，三种方案的对比情况如表4所示.可以看出，需求不足时方案G-F优于两个固定编组的对比方案.其他指标保持不变时，到达率可以表征需求水平.到达率为0.2λl时，需求水平较低，灵活编组方案的优越性体现在编组成本的节约上；当到达率增加到0.6λl时，与G-16相比优势在于节约成本，相比G-8的优势在于提高期望收益；当到达率增加到λl时，需求趋于饱和，此时各列车最佳的编组方案均为16编，G-F与G-16方案的收益性能一致.可见，灵活编组方案能够根据需求调节编组方案，从而对高铁运输供给能力进行调节，促进供需匹配，获得更好效益.

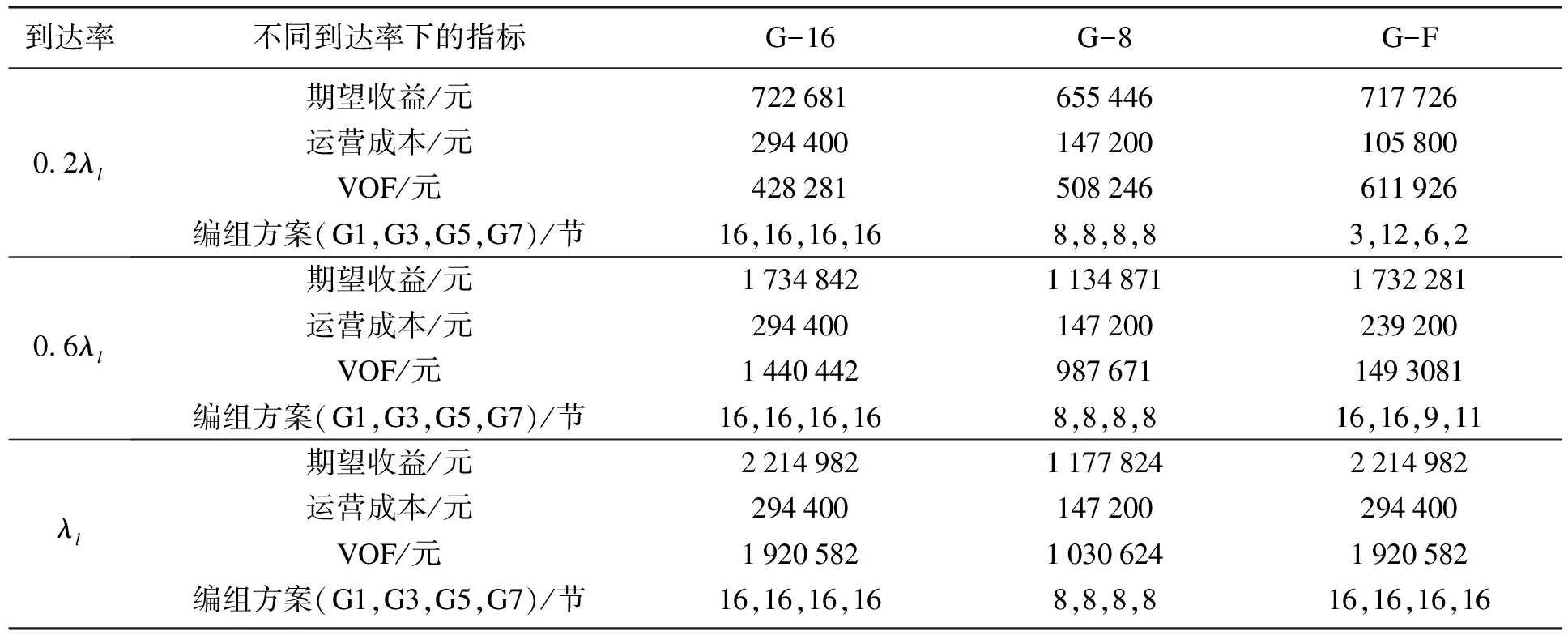
表4 不同需求强度下三种方案的对比

3.3 讨 论

保持其他数据不变，改变到达率、转移概率、编组成本等参数，研究灵活编组下的停售时间控制方案的收益性能变化规律，指导方案的实际应用.到达率和转移概率是描述市场需求规模和特征的重要参数，参数估计可参考文献[4].

1)不同到达率的情况.保持其他数据不变，通过乘以一定倍数改变各类旅客的到达率，得到不同到达率下的VOF和编组方案变化情况如图2、图3所示.随着旅客到达率的提高，需求规模增加，灵活编组方案中的编组单元总数相应增加，直到所有列车都达到最大编组单元数.但是列车G5的编组单元数并不是呈现单调增加的态势，这也反映出编组方案是4列列车综合考虑的优化结果.从VOF来看，G-F方案较固定编组方案的收益性能更好，尤其是在需求不饱和的状态下.当需求达到饱和时，各列车最佳列车编组方案都达到最大编组单元数，G-F方案与G-16方案的收益性能相同.

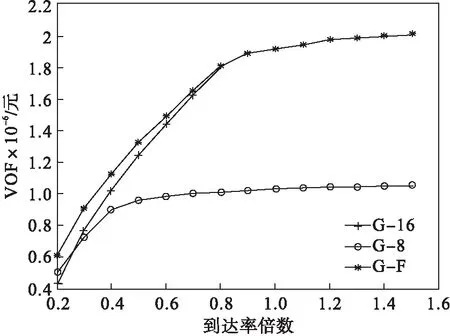
图2 不同到达率下的VOF变化规律

图3 不同到达率下的编组方案

2)不同转移购买概率的情况.保持其他数据不变，改变转移购买概率，得到VOF和编组方案变化情况如图4、图5所示.当各类别旅客的到达率保持不变时，转移购买概率变化直接影响着需求规模.转移购买概率越高，需求规模越大，总编组单元数越大，目标函数值也越大.可见旅客的转移购买行为对收益产生显著影响，实际运营中应重视旅客购买行为的研究.

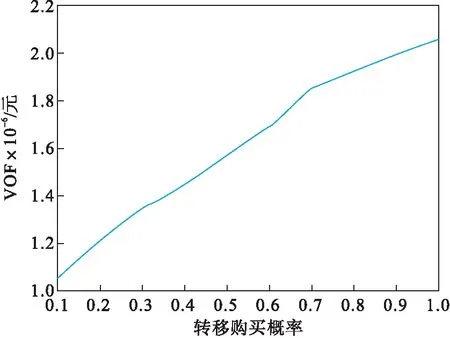
图4 不同转移购买概率下的VOF

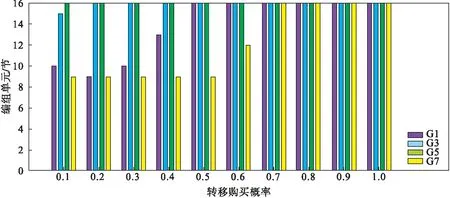
图5 不同转移购买概率下的编组方案

3)编组成本的影响.高铁列车的运营成本核算十分复杂.收益管理中通常不考虑运营成本，是因为固定运营成本远远大于单位旅客的边际运输成本.本文研究灵活编组下的收益管理方案，不能简单忽略增减列车编组时所产生的成本变化.本文提出的模型只需要核算出不同编组方案下运营成本的区别.用单位编组成本乘以不同系数，研究成本核算误差对最佳编组方案的影响.如表5所示，单位编组成本在3 680～6 900元这个区间内最佳编组方案保持不变.可见编组方案成本核算存在一定误差对最佳编组方案的影响并不显著.

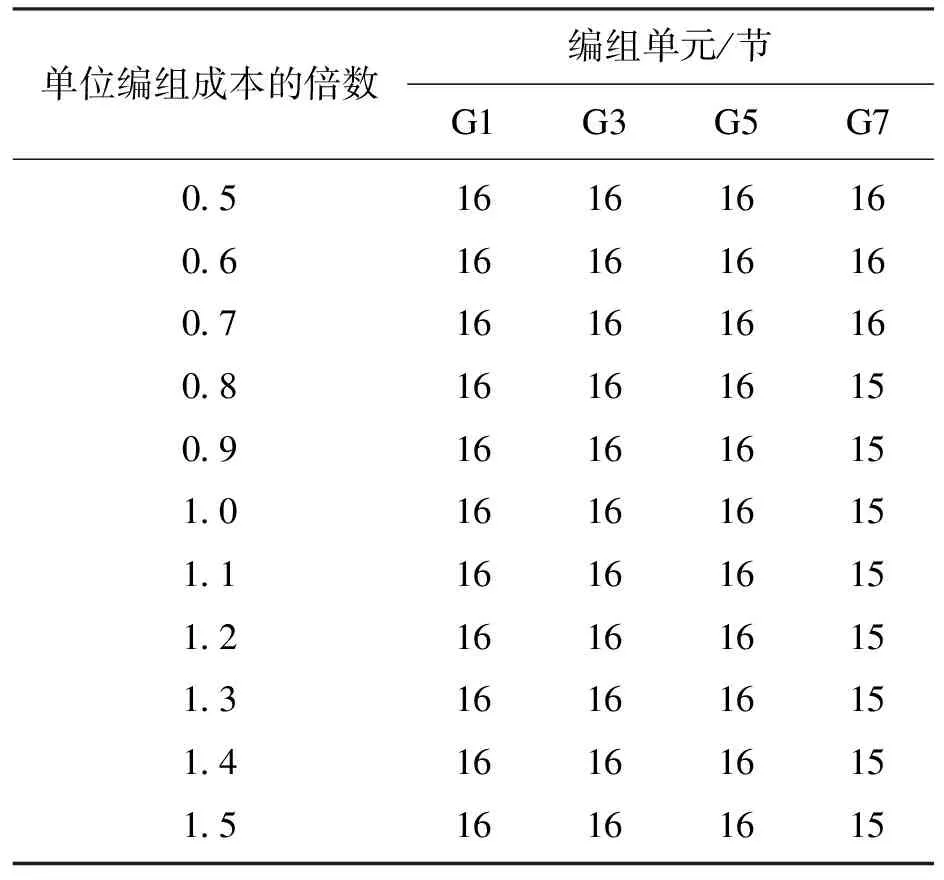
表5 编组成本对最佳编组方案的影响

4 结 论

1)本文采用偏好序选择模型刻画旅客购票选择行为，克服了MNL模型的IIA特性，提出了灵活编组下售票时间窗控制策略.综合考虑高铁线路上开行的多列车，通过寻求供给和需求的最佳匹配，实现运营企业获利最大化，得到各客票的停售时间策略和各列车的最佳编组方案.通过引入客票销售排序，将非线性规划模型转化为线性规划模型，利用CPLEX快速求解.实验结果表明，该模型能够得到获利最大化的客票销售时间窗控制策略和最佳编组方案，且求解速度能够满足应用需求.

2)与固定编组方案相比，灵活编组方案下的售票时间窗控制策略能够更好地权衡成本与收益，方案整体获利效果更好.当需求达到饱和状态后，各列车最佳编组方案均达到最大编组单元数，灵活编组下的售票时间窗控制策略与16编固定编组具有相同获利效果.

3)转移概率对需求规模和需求特征具有显著影响.数值实验表明：转移概率越大，需求规模越大，使得编组方案越趋向大编组，目标函数值也越大.可见旅客的转移购买行为对收益产生显著影响，实际运营中应重视旅客购买行为的研究.编组方案成本核算对最佳编组方案产生一定影响，但是影响并不灵敏.实际运用中，可以允许一定的核算误差.