考虑不完美维护的视情维修和备件订购联合策略优化
赵 斐, 李 鑫, 郭 明
(1.东北大学 秦皇岛分校 管理学院, 河北 秦皇岛 066004; 2.东北大学 工商管理学院, 辽宁 沈阳 110819)
工业4.0时代智能传感器的应用实现了对系统健康状态的实时监控,为设备维修决策提供了大量数据,进一步将视情维修策略(condition-based maintenance,CBM)提升到一个新的高度[1-3].视情维修利用反映系统健康状态的实时信息,依据系统当前工作状态采取相应的维护保养以及维修措施,建立相关维修模型进行决策,从而科学、合理、有效地安排维修活动.因此,视情维修策略有助于提高系统可靠性和可用度,降低维修费用.然而,维修活动与备件库存管理密切相关,维修活动导致备件消耗,而备件支持维修活动顺利开展[4].为此,也有少量学者对单部件系统视情维修和备件联合策略优化开展研究[5-6].
在工程实践活动中,根据系统的修复程度不同,通常将维护分为完美维修、不完美维护和最小维修.完美维修即系统通过维护活动恢复至全新状态,最小维修即维修后只能恢复到故障前状态;可是,在工业界中不完美维护活动应用更为普遍,即介于完美维修和最小维护之间,经不完美维护减缓系统的退化过程.不完美维护已受到学者们的关注,Kijima等[7]和Nakagawa等[8]分别提出采用虚拟役龄模型、失效率增加模型描述不完美维护后系统的退化过程;在此基础上,Zhou等[9]结合上述两种模型提出不完美维护混合模型,并通过数值实例验证了模型的合理性.不完美维护模型主要从虚拟役龄、失效率两个方面考虑不完美维护的影响;然而,均无法准确刻画在实际生产过程中不完美维护活动对系统随机退化过程的影响.为此,Guo等[10]基于Wiener过程建立维护决策模型,引入残余退化量模型表征不完美维护活动改善系统健康状态能力逐渐减弱的趋势.Zhang等[11]使用退化率函数代替失效率并引入随机改进因子,建立一种新的不完美维护模型.基于剩余寿命预测的不完美维护研究仅考虑维修对退化率和退化量的单一影响,针对这一问题胡昌华等[12-13]提出一种同时考虑不完美维护活动对退化量和退化率影响的退化建模.本文在同时考虑系统退化量和退化率的前提下,使用维纳过程建立维修决策模型,退化率更新函数选择指数函数描述不完美维护后对系统实际退化轨迹的影响.
利用状态监测得到的系统实时退化数据,预测剩余寿命并用于维修和备件订购决策,体现了故障预测与健康管理技术的内涵[14-16].已有学者在预测剩余寿命基础上对维修和备件联合优化策略展开研究.Wang等[17]提出了一种基于实时预测寿命信息的联合订货替换策略,通过预测剩余寿命获得订单替换决策及更新替换时间,建立序贯优化模型确定最优的订货点.蒋云鹏等[18]对剩余使用寿命进行预测,建立预测信息下的序贯优化模型和联合优化模型,通过轴承加速寿命试验证明联合优化模型下的更换时间和备件订购时间优于序贯优化模型结果.Si等[19]研究了系统更换和备件订购问题,通过推导剩余寿命的概率密度函数,建立可靠性约束下的成本率模型.上述研究仅仅是将预测剩余寿命用于维修策略或备件策略,而未将预测得到的剩余寿命同时运用于维修决策和备件订购决策上[20].
本文针对单部件系统分别设置预防性更换阈值和备件订购阈值,用于系统何时执行不完美维护和预防性更换决策,何时订购备件决策.结合系统更新时不同事件的发生概率,利用更新报酬理论对单部件系统维修和备件订购联合策略建立决策优化模型,并设计离散仿真事件算法求解;最后,通过数值仿真实验进行验证,并对不同参数进行灵敏度分析.
1 不完美维护下基于剩余寿命预测的视情维修和备件订购联合策略
1.1 问题描述
传感器每隔Δt时间监测系统退化状态获得实时的健康信息,初始时刻0时系统退化状态为0.考虑到不完美维护(imperfect maintenance, IPM)同时对系统退化量和退化率的影响,采用Wiener过程对系统退化过程进行分阶段建模.根据视情维修的控制限原则,根据检测时系统所处的不同健康状态执行不同的维修活动,即若退化量达到最小维修阈值ωm时,对系统进行最小维修,且仅考虑执行一次最小维修;若达到预防性维护阈值ωp时,对系统进行不完美维护或预防性更换(preventive replacement, PR);若超过故障更换(corrective replacement, CR)阈值ωl,则立即进行故障更换.其中,当系统在第k次IPM时刻jkΔt达到预防性维护阈值ωp时,是否执行不完美维护需进一步决策;此时若系统剩余寿命rk,ωl大于预防性更换阈值TIPM,则考虑进行不完美维护活动,否则执行预防性更换,预防性更换时不完美维护次数为N.
无论是PR还是CR都是对旧系统的更换,显然均会产生备件需求,根据系统健康状态合理制定采购计划是关键点.考虑到备件由采购至到货需要经历一段时间,即提前期L,本文通过引入订购阈值Lo与提前期、预测剩余寿命比较构建备件订购的约束条件.若在时刻jkΔt系统剩余使用寿命rk,ωl与备件提前期L、订购阈值Lo满足条件rk,ωl≤Lo+L,则下正常订单,且备件经提前期L后到货入库;否则,不订购直至下次执行IPM时再进行判断.如果更换系统时,备件未订购,则下紧急订单,紧急订单提前期与正常订单提前期相比较小可忽略;若备件已经订购但是未到货,则直到备件到货后再更换,备件缺货将造成一定的经济损失,单位时间内的缺货成本为CP;如果更换需求产生时备件已到货正处于存储状态,则立即更换系统,因备件提前到达以单位时间的成本Ch产生存储费用.
检测间隔的不同会影响系统退化状态信息的获取,进而影响维修决策和备件采购决策,而预防性维护阈值的决定直接影响是否产生备件需求,因此本研究将检测间隔、预防性维护阈值作为决策变量进行优化.
1.2 不完美维护下的系统退化过程建模和剩余寿命预测
每隔时间Δt监测系统的健康状态,时刻tm=mΔt系统退化量为X(tm).由于考虑了不完美维护,为此采用Wiener过程对系统退化分阶段建模,将系统经过第k(0≤k≤N)次IPM后的退化量定义为
Xk(tm)=yk+μk(tm-jkΔt)+σBB(tm-jkΔt).
(1)
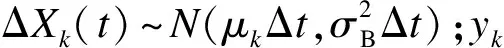
f(yk)=
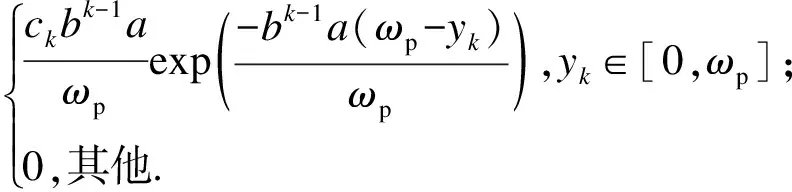
(2)
其中:a,b为超参数;ck=1/(1-exp(-abk-1)).
基于首达时间概念预测系统剩余寿命,定义系统退化量首次达到阈值ωi(i=m,p,l)的时间Rk,ωi为
Rk,ωi=inf(rk,ωi|X(jkΔt+rk,ωi)≥ωi|yk,rk,ωi>0).
(3)
进而,系统剩余使用寿命Rk,ωi服从逆高斯分布,对应的概率密度函数fk,ωl(rk,ωl|yk)和累积分布函数Fk,ωl(rk,ωl|yk)分别为
fk,ωl(rk,ωl|yk)=
(4)
(5)
剩余寿命Rk,ωl的期望和方差分别为
(6)
(7)
2 不完美维护联合策略优化建模
每次以成本Ci对系统进行状态监测,X(tm)≥ωl时系统执行故障更换,每次故障更换成本为CCR;若ωl>X(tm)≥ωp,则每次以成本CIPM执行不完美维护或者以成本CPR对系统进行预防性更换;若ωp>X(tm)≥ωm,则每次以Cm执行最小维修.从而确定系统更换有两种相互独立的情形:一,系统退化量满足条件ωl>X(tm)≥ωp且剩余使用寿命rN+1,ωl
2.1 更新事件的发生概率
系统在(m+1)Δt时刻执行最小维修概率为
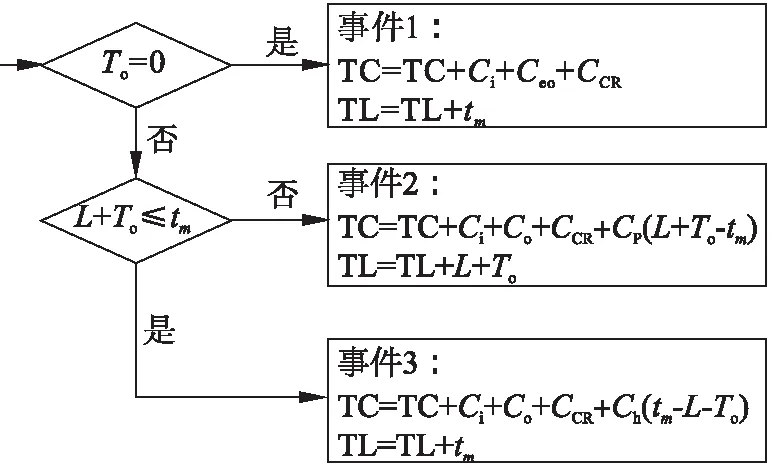
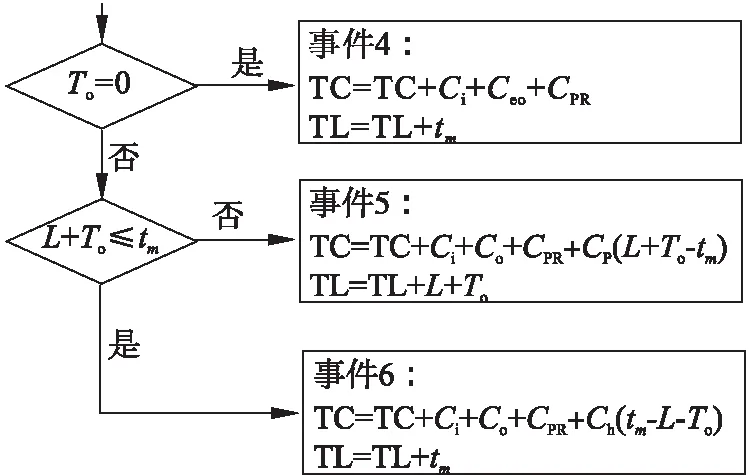
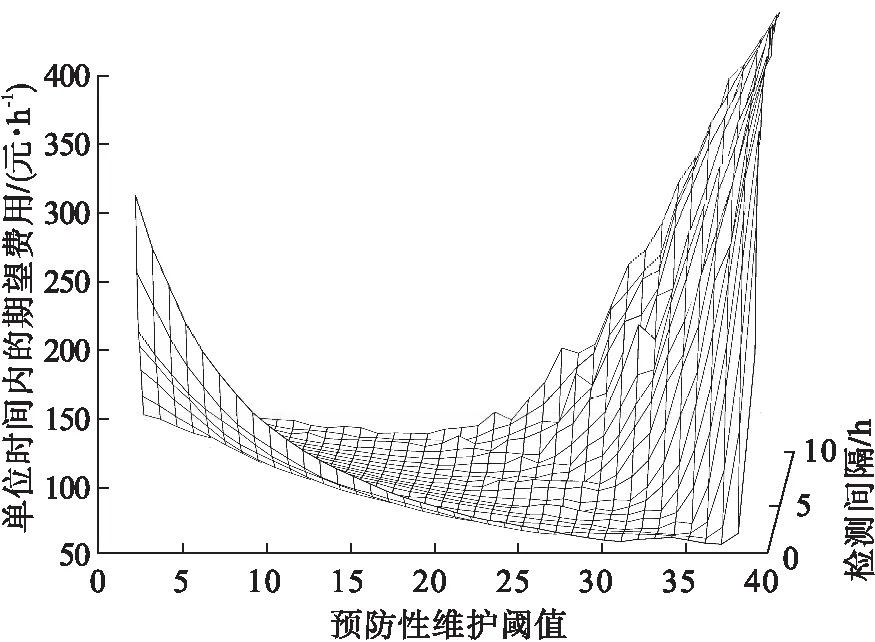
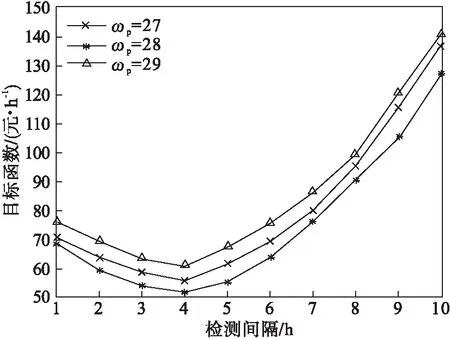
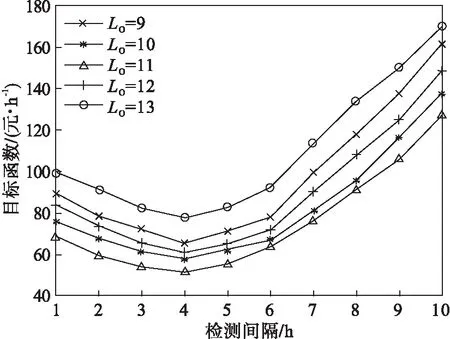
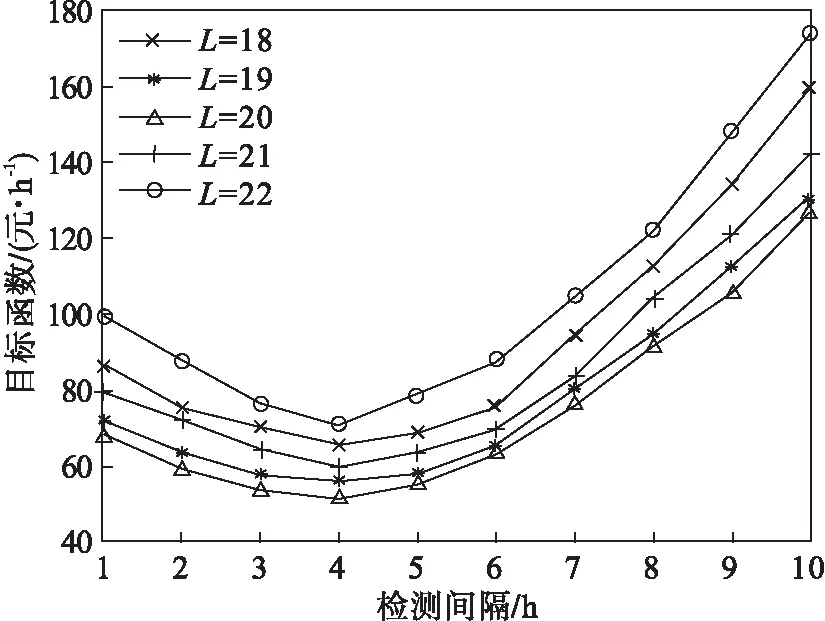
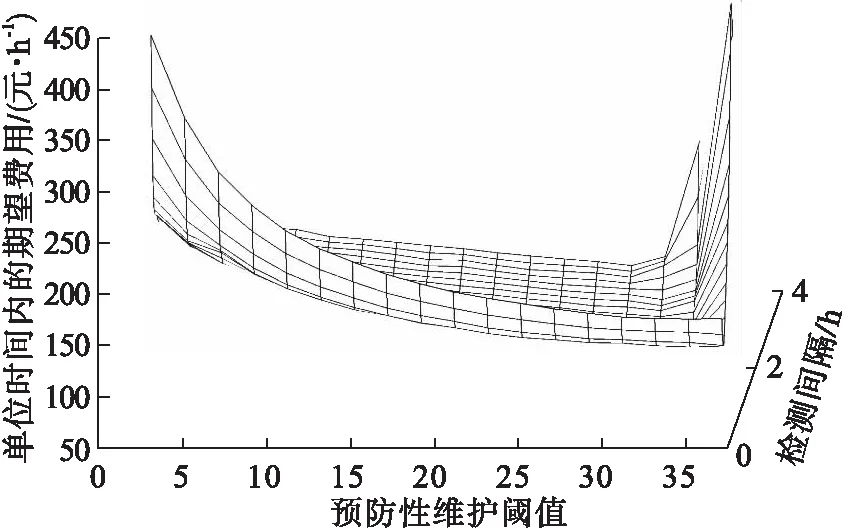
Pm=P(X(mΔt)<ωm∩ωm (1-F0,ωm(mΔt))(1-F0,ωp((m+1)Δt))- (1-F0,ωm(mΔt))(1-F0,ωm((m+1)Δt)). (8) 系统在jkΔt时刻执行不完美维护的概率为 (9) 系统故障更换概率PCR: (10) 其中,n=1,2,…,N. 系统预防性更换概率PPR: (11) 式(8)~式(11)中: (12) (13) (14) 利用监测得到的系统健康状态,预测系统剩余使用寿命并判断是否在该监测点进行备件订购.根据rk,ωl与订购阈值Lo对比:rk,ωl>L+Lo,则备件未订购,此时订购时刻To=0,则通过紧急订单满足系统的备件需求;如果Lo 备件未订购概率: P(rk,ωl>L+Lo)= (15) 备件已订购未到概率: P(Lo (16) 备件已订购且到货的概率: P(0 (17) 根据系统退化状态和备件状态,分析并推导各更新事件发生概率和对应的期望成本EC和期望时长ET,并利用更新报酬理论构建费用-时间率联合决策模型. 事件1:系统执行故障更换且备件未订购: (18) (19) 事件2:系统执行故障更换且备件已订未到货: (20) rk,ωl>Lo). (21) 事件3:系统执行故障更换且备件已到货: (tm-To-L)Ch)×PCRP(Lo>rk,ωl>0), (22) (23) 事件4:系统执行预防性更换且备件未订购: PPRP(rk,ωl>(L+Lo)), (24) (25) 事件5:系统执行预防性更换且备件已订购未到货: (26) (27) 事件6:系统执行预防性更换且备件已到货: (28) (29) 式中,To为备件订购时刻. 采用更新报酬理论建立目标函数: (30) 通过设计离散事件仿真算法求解最优的决策变量,即检测间隔和预防性维护阈值.结合所提出的联合策略和构建的优化模型,图1给出了离散事件仿真算法的流程图,详细步骤如下所示: 图1 离散事件仿真算法 步骤1 设置初始漂移系数μ0,扩散系数σB,初始残余退化量y0,系统故障更换阈值ωl=40,最小维修阈值ωm=1,预防性维护阈值ωp=1,最大迭代次数imax,预防性更换阈值TIPM,提前期L,备件订购阈值Lo,以及所有成本参数. 步骤2 设置预防性维护阈值ωp=ωp+0.5,检测间隔Δt=0.5. 步骤3 设置初始总期望成本TC=0,总期望时间TL=0,迭代次数i=0,检测间隔Δt=Δt+0.5. 步骤4 设置当前时刻tm=0,系统退化量X(tm)=0,备件订购时间To=0,不完美维护次数k=0,检测间隔Δt和预防性维护阈值ωp不变,运行次数i=i+1. 步骤6 将tm时刻的系统退化量X(tm)分别与最小维修阈值ωm、预防性维护阈值ωp和故障更换阈值ωl进行对比.若X(tm)≥ωl,则转到步骤7;若X(tm)<ωl,则返回步骤5,系统继续叠加退化量,总期望成本TC=TC+Ci.若ωl>X(tm)≥ωp,则转到步骤8和步骤9;若X(tm)<ωp,则返回步骤5.若ωp>X(tm)≥ωm,则系统执行最小维修,总期望成本TC=TC+Cm;若X(tm)<ωm,则返回步骤5. 步骤7 如果X(tm)≥ωl,则系统执行故障更换,如图2所示,总期望成本TC=TC+CCR.若To=0,则备件未订购,事件1发生,总期望成本TC=TC+Ceo.若To 图2 离散事件仿真算法的Box A 步骤8 如果ωl>X(tm)≥ωp,则根据式(6)预测系统剩余寿命.若rk,ωl>L+Lo,则订购时刻To=0;若rk,ωl≤L+Lo,且To=0,则订购时刻To=tm,总期望成本TC=TC+Co. 步骤9 如果ωl>X(tm)≥ωp,则根据式(6)预测系统剩余寿命.若rk,ωl≥TIPM,则系统执行不完美维护,维修后系统退化量为yk,根据退化模型中的μk=(exp(k)+1)μ0更新漂移系数μk,不完美维护次数k=k+1,总期望成本TC=TC+CIPM,否则转到步骤10. 步骤10 如果rk,ωl 图3 离散事件仿真算法的Box B 步骤11 判断运行次数,若满足i=imax,则计算EC(ωp,Δt)并记录,否则返回步骤4. 步骤12 若EC(ωp,Δt) 设置数值仿真实验对决策模型进行仿真优化,分析不同参数对目标函数和决策结果的影响,验证模型有效性. 系统退化参数如表1所示. 表1 退化参数 成本参数如表2所示. 表2 成本参数 图4 目标函数与决策变量之间关系 在假定成本参数和退化参数不变的情况下,分别探讨预防性维护阈值ωp、预防性更换阈值TIPM、订购阈值Lo、提前期L变化时,检测间隔Δt与目标函数之间的关系. 1)ωp变化时Δt与目标函数之间的关系,如图5所示.预防性维护阈值ωp决定设备何时执行不完美维修,当ωp过小时,提前进行不完美维修,维护频率提高,维修后部件退化加快,提前进行设备更换,设备总运行时间降低;当ωp过大时,由于不完美维修会造成退化率变大,设备不完美维修次数减少,设备退化量超过故障更换阈值,更换成本增加.这与图5中结果一致,如果检测间隔Δt不变时,当ωp=27或ωp=29时,都会增加单位时间内的成本.而对于任一预防性维护阈值而言,目标函数均呈现出随检测间隔先降低后增加的趋势,这与对图4的分析一致. 图5 预防性维护阈值对目标函数的影响 2)TIPM变化时Δt与目标函数之间的关系.在每次不完美维护前,比较预测剩余寿命与预防性更换阈值TIPM,以决策是否对设备执行不完美维护活动.从图6中结果可看出,当TIPM小于13时,预测剩余寿命总是大于TIPM,不完美维修多次执行,导致设备未及时进行更换,造成设备故障更换成本升高;当TIPM大于13时,设备执行几次不完美维修后便需要进行预防性更换,设备利用率降低.因此,TIPM合理设置可以使设备避免维修过多和故障成本过高. 图6 预防性更换阈值对目标函数的影响 3)Lo变化时Δt与目标函数之间的关系.由图7结果可看出,订购阈值变化时目标函数值随检测间隔先降低后增加.其中, 订购阈值Lo过小则备件订购提前并且提前到货,备件库存成本过高,从而增加期望总成本;反之,设备执行预防性更换或故障更换时,Lo过大导致备件处于未订购状态,则需要通过紧急订单满足备件需求,故增加期望总成本,导致目标函数增加. 图7 订购阈值对目标函数的影响 4)L变化时Δt与目标函数之间的关系.如图8所示,提前期L过小则备件订购后提前到货,备件存储时间变长,库存成本过高;提前期L过大,系统执行预防性更换或故障更换时,如备件已订购但未到货,此时缺货成本增加. 图8 提前期对目标函数的影响 图9 目标函数与决策变量之间关系 通过对比两组数值仿真实验的结果发现,模型1的最优长期期望费用率小于模型2,这是由于模型1策略中不完美维护使系统避免了维修不足的实际问题,延长了系统役龄,使系统成本率最低. 1)本文对单部件系统提出视情维修和备件订购的联合策略,其中维修策略采用控制限策略,考虑了不完美维护对系统退化的实际影响,使用Wiener过程对系统退化分阶段建模,推导最小维修、不完美维护、预防性更换和故障更换概率. 2)将预测的剩余寿命分别应用于维修决策和备件订购决策中,在每次不完美维护时刻预测系统剩余使用寿命并分别对比预防性更换阈值和订购阈值,确定是否执行预防性更换、订购备件决策,结合维修方式和备件状态推导各事件发生概率,构建成本率目标函数. 3)通过设计离散事件仿真算法优化决策变量Δt和ωp,并对不同参数进行灵敏度分析;同时,与未考虑剩余寿命预测的联合决策模型进行比较,结果表明所提出的联合策略能够有效降低系统的成本.
2.2 构建费用-时间率联合决策模型
3 离散事件仿真算法设计
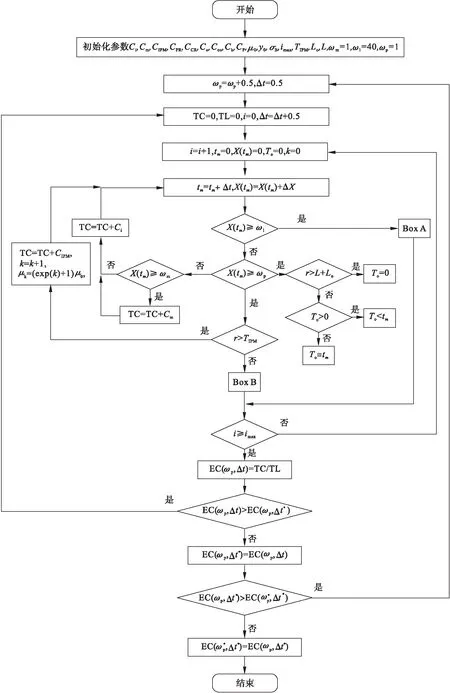
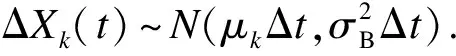
4 算例分析
4.1 参数设置


4.2 最优解分析
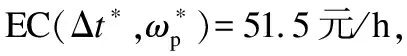
4.3 对比分析
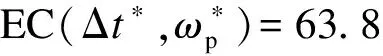
5 结 论

