基于PHF-LSM-MT法岩石材料细观边界建模与水力裂缝扩展研究
李 明, 赵 岐, 陈 昭, 梁 力
(东北大学 资源与土木学院,辽宁 沈阳 110819)
水力压裂技术作为油气增产手段已被广泛应用于实际工程并取得显著效果.目前关于水力压裂扩展规律的研究手段可分为:物理试验、理论研究和数值模拟.其中物理试验是探究岩石水力裂缝扩展特征、分布形态以及影响起裂压力因素的有效方法.例如Zhang等[1]采用三轴水力压裂试验研究天然裂缝的空间位置和倾角对水力裂缝扩展形态的影响.
在理论研究方面,已有的方法多基于断裂力学的相关研究成果,如PK模型、KGD模型[2]和PKN模型[3]等.物理试验虽然可以较真实地模拟原位裂缝扩展形态,但成本较高,理论求解虽然可以得到精确解,但均建立在严格的假设基础上.
数值模拟方法具有低成本高收益的特点,可以弥补物理试验和理论研究的不足.例如:内聚区模型[4]、弥散裂缝模型[5]、相场法[6]等.此外不同方法的结合亦可解决水力压裂的相关问题,如Yan等[7]采用有限元法耦合离散元法实现了水力压裂过程的模拟,并通过物理试验证明压裂裂隙与地应力的关系.
岩石的宏观力学特性会受到细观结构特征的影响[8],因此有必要考虑天然岩石细观边界特征对力学特性和水力压裂过程的影响.如Li等[9]结合水平集法(level set method,LSM)建立了含有圆形、椭圆形以及空间非均质的岩石材料模型,并结合基于渗透率修正的水力压裂模型(permeability-based hydraulic fracture, PHF)分析了水力裂缝的传播过程.
已有的PHF-LSM法可以考虑颗粒分布对水力压裂过程的影响,但其中未考虑积分点处细观边界特征.本文结合柏林噪声和椭圆水平集方程,建立以颗粒半径为参数的非规则颗粒建模方法,基于重心坐标法[10]实现非规则颗粒填充,并引入Mori-Tanaka(MT)均匀化方法[11]考虑高斯积分点处的细观边界特征.最终,建立PHF-LSM-MT法的非均质岩石材料的水力压裂数值计算模型,并分析考虑细观特征的非规则岩石材料的水力裂缝特性.
1 非规则颗粒边界方程
在本文的研究中假设非规则颗粒Ω由颗粒包含的椭圆形(Ω0)和非规则圆环(Ω1)组成,如图1所示.
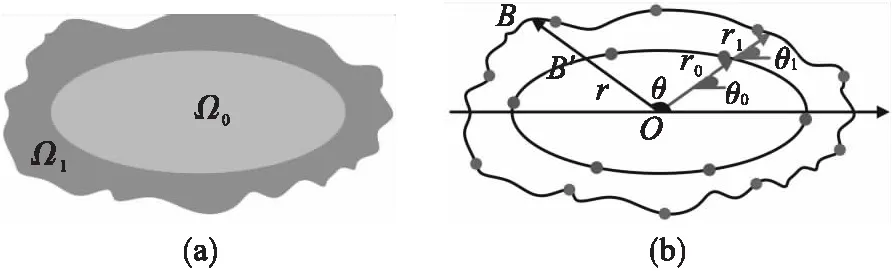
图1 非规则颗粒等效分解
极坐标系下的非规则颗粒边界的水平集方程,如式(1)所示.
φi(θ)=r0(θ)+r1(θ) (0<θ≤2π).
(1)

2 颗粒填充和碰撞检测
假设岩石内部的包裹体之间不重叠,在二维区域内生成多个非规则颗粒时,颗粒之间的关系可分为:包含、相交、相切和相离,如图2所示.本文通过包裹体边界上的点是否在其他包裹体中的方法来判别颗粒间的相对位置关系.
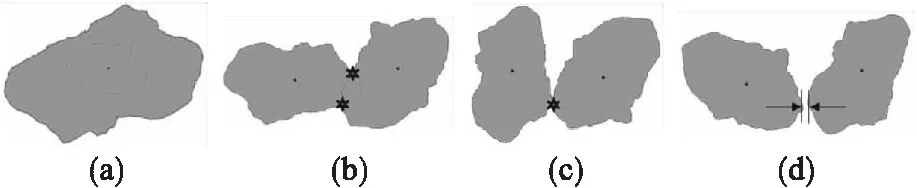
图2 非规则颗粒位置关系
2.1 非规则颗粒接触判定
将颗粒离散为三角形单元集合,边界由线性差值简化,如图3a所示,其面积由式(2)计算.

图3 非规则颗粒碰撞检测方法
(2)
式中:Sj为第j个三角形的面积;N为三角形个数,本文建模过程中取N=360.
重心法原理如图3b所示,直角坐标系下三角形O1O2O3的顶点坐标向量分别为O1,O2,O3,点P′在三角形内部的权重公式为[13]
P′-O1=u(O3-O1)+v(O2-O1).
(3)
式中:u,v均为常数,当u=0,v=0时,P′代表O1点;当u=0,v=1时,O′代表O2点;当u=1,v=0时,P′代表O3点.根据图中P′,P1,P2,P3可知,如果判断点在三角形内部,则必须要满足①u≥0;②v≥0;③u+v≤1,取等号时,表示判断点在三角形边上.令V1=(P′-O1),V2=(O3-O1),V3=(O2-O1),将式(3)的等式两边分别乘以V2和V3即可得到v和u.
2.2 非规则颗粒间的位置关系
建立非规则颗粒I1和I2并分别包含以下信息:中心坐标(x0,y0);长半轴(a);短半轴(b);颗粒倾角(β);圆环厚度均值(A);颗粒边界顶点坐标(xj,yj).xj和yj分别代表第j个顶点的x坐标和y坐标,其中1≤j≤360.顶点坐标的储存顺序按照逆时针方向,当长半轴与水平夹角为0°时记为第一个顶点坐标.
在调用颗粒信息时采用以下书写格式(调用第1个颗粒的中心坐标记为I1(x0,y0)):
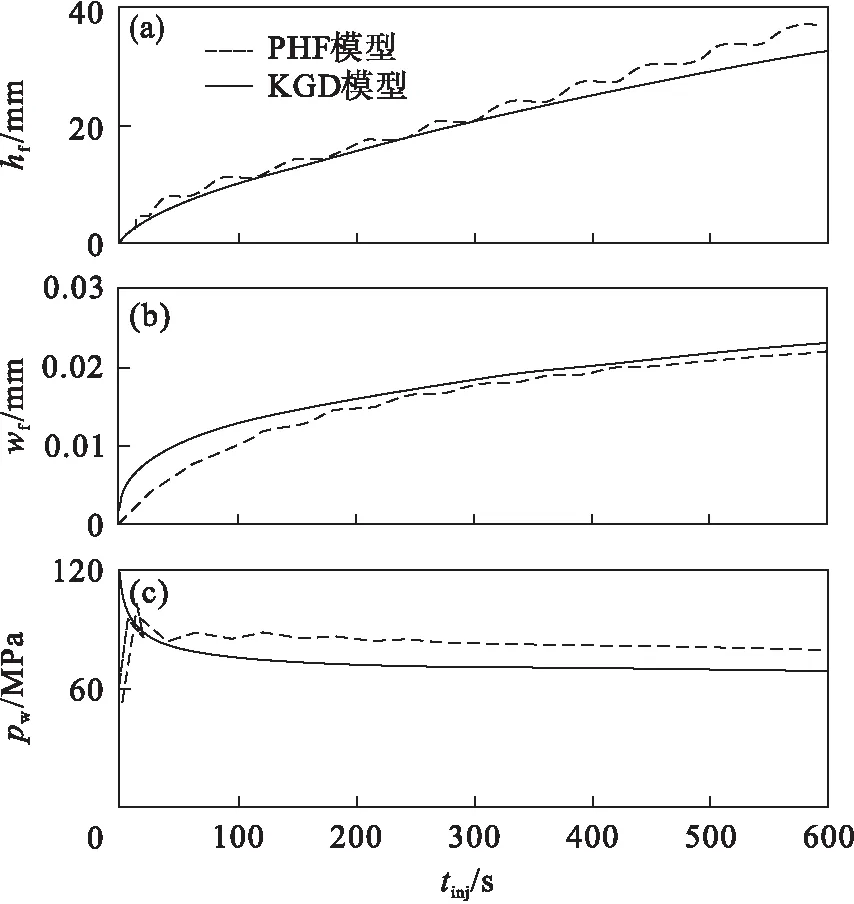
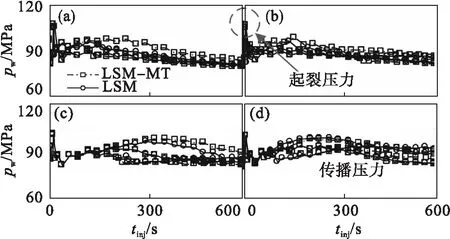
①颗粒I1包含颗粒I2:I2(x0,y0),…,I2(x360,y360)均在I1内部,判别式恒成立.②颗粒I2包含颗粒I1:I1(x0,y0),…,I1(x360,y360)均在I2内部,判别式恒成立.③颗粒I2与颗粒I1相交:I2(xk,yk),…,I2(xl,yl)均在I1内部,共(l-k+1)个判别式成立;或I1(xm,ym),…,I1(xn,yn)均在I2内部,共(n-m+1)个判别式成立,1≤k 当颗粒在进行碰撞判定时会出现图4所示的4种特殊情况.通过细化颗粒边界和控制最小距离Dmin避免图4所示现象,其中Dmin与长半轴(a)和厚度均值(A)之间的关系见式(4). 图4 非规则颗粒间特殊位置 Dmin+Dgap≥Iia+IiA(Dgap≥0). (4) 式中:Dgap为颗粒间缝隙;Iia和IiA分别为新颗粒Ii的长半轴和厚度均值. 以图5所示五边形为例,在确定I2的中心点V0不在颗粒I1内部的基础上,计算向量OV0与水平方向夹角θt,在颗粒I1中一定可以找到2个连续的顶点坐标Vj+1(xj+1,yj+1)和Vj(xj,yj),该顶点坐标和I1中心点连线与水平方向的夹角分别为θj+1,θj,三者之间的关系满足θj+1≥θt≥θj.OVt的长度采用式(5)和式(6)计算,其中Vt为OV0与Vj+1Vj的交点. 图5 非规则颗粒间距计算 |OVj×OVj+1|=|OVj×OVt|+|OVt×OVj+1|, (5) (6) Dmin=min{|OV0|-|OVt|,|V0V1|,…,|V0V360|}. (7) 通过式(4)和式(7)可计算不同颗粒间的最小距离Dgap.采用Processing软件在给定区域内填充不同几何特征的非规则颗粒模型,如图6所示,其中a=(2.0~30.0)mm,b=(0.0~1.0)×a,β=(0~2π). 图6 非规则颗粒填充 已有的基于水平集法建立的有限元模型如图7所示.由于积分点的有效区域内会被赋值为单一材料属性,颗粒边界会呈现“锯齿状”,如图7b所示. 图7 隐式建模方法 以图8所示含有随机分布非规则颗粒(Dgap>0),边长为l的岩石模型为例.该模型受到初始水压力(pw)、水平和垂直方向应力(σh,σv)作用,模型底边受到垂直方向约束,底边中心位置为固定约束.模型中间施加注水荷载.由式(1)建立的水平集方程为 图8 非均质岩石力学模型 I={x∈Ω:φi(x)≤0} (i=1,2,…,n), (8) φi=(x(r,θ))=φi(θ)-r. (9) 式中:x为平面Ω内积分点的位置向量;当φi<0时表示积分点在颗粒内部,反之,当φi>0时表示积分点在颗粒外部,当φi=0时表示积分点在颗粒边界上. 当积分点的有效区域wsub×hsub内含有材料边界时(如图7中积分点i1,i2,i5,i9),已有的简化方法是通过阶跃函数、线性函数和非线性函数对材料进行过度处理[14],该三种方法均不能考虑材料边界特征的影响.本文采用均匀化方法对高斯积分点有效区域进行均匀化处理,以消除边界“锯齿状”现象.均匀化后的等效材料参数Λ由式(10)表示,即 Λ=f(I0,I1,…,In). (10) 其中:I0代表基质的材料参数;I1,…,In代表颗粒的材料参数.PHF模型中共考虑了4种材料参数,其中弹性参数(E,v)采用MT[15]法计算,即: (11) (12) Tr={I+Sr:(Ir-I0)}-1(r=1,…,n). (13) 式中:I和I0是四阶单位张量和基质的有效刚度张量;Sr代表第r相颗粒的四阶Eshelby张量[16]. 文献[17]的研究表明等效材料弹性参数均在Voigt上限(VR+)和Reuss下限(VR-)之间,即 (14) (15) 式中:Ma=κ1/κ0;κ0和κ1分别为基质和颗粒的初始渗透系数;φ1为颗粒的体积分数;ζ是与颗粒形状有关的参数,本文采用的非规则颗粒是以椭圆形为基础,因此计算中ζ取0.5[19]. 本文依托ABAQUS软件进行数值模拟,通过用户子程序实现图9所示积分点有效区域参数均匀化.步骤如下:①通过子程序UEXTERNALDB读取非规则颗粒参数信息,根据式(11)建立隐式材料边界模型,见图9a.②通过子程序SDVINI调用单元信息,根据积分点类型获得坐标信息和有效区域范围wsub×hsub,见图9b.③将有效区域离散成wmin×hmin子网格并计算每个子网格中基质和颗粒占有效面积的体积分数φ0和φ1,见图9c.本文取值wmin=wsub/10,hsub=hmin/10.④根据式(11)、式(14)和式(15)对材料参数均匀化,并重新赋值到积分点,见图9d.⑤重复循环完成所有单元检测. 图9 积分点参数均匀化 通过建立颗粒边界并对不同区域赋值材料属性得到模型(显式模型),其结果作为对照组,验证LSM-MT方法的可行性.以模型垂直方向杨氏模量Ey为例,对比LSM法与LSM-MT法建立模型(隐式模型、改进模型)相对于显式模型计算结果的相对误差er=|(Ξim-Ξex)/Ξex|和绝对误差εr=Ξim-Ξex,其中Ξim为隐式方法计算结果,Ξex为显式方法计算结果,其相对误差和绝对误差记为eri和εri,改进模型的相对误差和绝对误差记为erm和εrm. 三种方法建立的含有非规则颗粒分布的有限元模型如图10所示,可以看出隐式模型中材料边界呈“锯齿状”,而改进模型中材料边界有明显改善.同时采用表1所示包裹体的几何参数,建立基质和颗粒的杨氏模量分别取值20 GPa和80 GPa,泊松比分别取值0.25和0.2的模型.通过不同方法计算的等效模量如图11所示,结果表明,等效弹性参数Ey均落在VR上下界限内,且在MT法的解上下波动.三种模型的Ey均随颗粒体积分数增加而增大. 图10 基于不同建模方法有限元模型 表1 非规则颗粒几何参数取值 图11 体积分数改变对弹性模量的影响 两种隐式模型在不同体积分数下的相对误差和绝对误差如图12所示. 图12 不同方法的有效模量误差对比 结果表明两种模型计算得到的弹性模量均大于理论值,且LSM-MT法的计算误差均小于LSM法.因此本文建立的LSM-MT建模方法可有效考虑材料边界分布特征,并增加计算结果的精度. 采用基于Biot固结理论建立的PHF水力压裂数值计算模型,结合LSM-MT法建立含有非规则颗粒的岩石模型实现其水力压裂过程的模拟. 在深部岩层中水力压裂过程是渗流与裂隙岩体相互作用的过程,其平衡方程、渗流方程、几何方程、物理方程和有效应力原理如下[9]: σij,j+ρfi=0 (i,j=1,2,3), (16) (17) (18) (19) (20) (21) 式中:参数κave=(κmax+κ0)/2,κmax和κ0分别为渗透系数上限值和初始值;κδ=(κmax-κ0)/2;Rm和σm分别为岩石材料的抗拉强度和平均有效应力;ξ为损伤系数;μmix为混合黏滞系数;krw为水相对渗透率,采用Corey[20]关系计算,即 krw=krw0((Sw-Swi)/(1-Swi-Sorw))Nw. (22) 式中:krw0,Sw,Swi,Sorw和Nw分别为水相对渗透率端点、饱和度、束缚水饱和度以及剩余油饱和度;本文计算中krw0=0.5,Nw=3.66,Swi=Sorw=0.15[20]. PHF-LSM-MT水力压裂数值模型的建立采用ABAQUS软件二次开发功能,流程如图13所示.子程序SDVINI包含8个状态变量:弹性模量(E)、泊松比(v)、基岩抗拉强度(Rm)、有效渗透系数(κ)、基岩密度(ρ)、饱和度(S)、孔隙比(e)和混合黏滞系数(μmix).依据式(11)实现非规则颗粒材料分布,并采用均匀化方法修改材料边界处积分点有效参数.子程序USDFLD用来接受SDVINI传入的状态变量,并通过式(21)修正等效开裂区域渗透系数. 图13 PHF-LSM-MT模型算法实现 以边长为100 mm的二维均质岩石模型为例,将PHF模型计算得到的水力裂缝扩展形态与KGD模型的理论解进行对比.力学模型如图8所示,材料参数采用某地下3 088 m的实测数据,如表2所示. 表2 基岩材料力学参数 模型受到初始水平和垂直方向地应力为σh= 61.47 MPa和σv= 71.62 MPa,初始水压力pw= 52 MPa,注水速度qinj=0.001 mm/s,注水时间为600 s.由于PHF模型是通过修改破坏区渗透系数表示裂缝扩展过程的一种弥散裂缝模型,因此模拟过程中没有出现真实的裂缝,计算得到的等效开裂区域发展过程如图14所示.采用PHF法计算的裂缝等效高度hf为开裂区域的垂直方向范围,裂缝等效宽度wf为注水点位置裂缝开裂区域的水平方向位移差(ur-ul). 图14 裂缝等效开裂发展过程 基于KGD理论模型的水力裂缝高度hf、裂缝开度wf和注水压力pw的理论解如式(23)~式(25)[9]所示: (23) (24) (25) 式中:G为剪切模量;当水力裂缝为双向扩展时,参数a,b,c分别为0.48,1.32和1.91[9]. 通过PHF模型计算的水力裂缝等效高度、等效开度和注水点水压力随注水时间变化过程与KGD理论解对比如图15所示. 图15 水力裂缝特征验证 该计算结果表明PHF模型计算的数值解与解析解基本吻合.由于KGD模型假设裂缝处于无限半空间中,而在注水过程中随着裂缝不断扩展并逐渐接近模型边界,导致两者有一定偏差. 建立图8所示的非均质岩石的数值计算模型,边界条件与均质岩石情况相同.计算中假设包裹体不易开裂,所用材料参数如表3所示.每种包裹体体积分数包括3个随机算例. 表3 包裹体材料力学参数 当注水时间为600 s时,基于PHF-LSM-MT法计算的非均质岩石模型等效开裂区域如图16所示.该结果表明:当传播路径存在包裹体时,水力裂缝在材料交汇处发生变化.当包裹体与裂缝发展方向的有效面积和倾角均较大,裂缝沿包裹体表面扩展,如图16a和图16c所示;当包裹体在裂缝发展方向的有效面积较大但倾角较小时,包裹体会阻止裂缝扩展,随注水时间增加,裂缝沿包裹体表面发展,最终绕过包裹体,如图16c和图16d所示;当包裹体在裂缝发展方向的有效面积较小时,裂缝直接绕过包裹体继续发展,如图16b和图16d所示. 图16 非均质岩石水力裂缝模型等效开裂区域 注水点位置的水压力变化曲线如图17所示,两种建模方法得到的结果均呈现先增加至起裂压力后降低至传播压力的趋势,与已有的计算结果一致[14]. 图17 注水点单元水压力发展历程 注水位置应力路径变化如图18所示.结果表明包裹体分布影响了应力路径初始应力状态.当注水时间增加时,平均有效应力p由初始状态降低至零(受压状态),随后开始增加(受拉状态).剪应力q在开裂过程处于降低状态,最终为零. 图18 注水点单元应力路径发展历程 图19给出了不同体积分数,两种方法计算的起裂压力.当包裹体体积分数相同时,三种随机工况均表明改进模型计算得到的起裂压力高于隐式模型,绝对误差最大值为0.101 MPa.基于线弹性理论的起裂压力理论解为pb=3σh-σv+Rm= 116.962 MPa[9],与本文中隐式模型和改进模型计算结果的相对误差分别在8.98%~12.02%和8.94%~11.98%之间. 图19 不同方法计算的起裂压力 1)建立了基于柏林噪声的非规则几何边界的水平集方程,采用重心坐标法检测颗粒碰撞,实现以粒径、长短半轴比、倾角和填充率为参数的非规则颗粒填充算法. 2)在已有LSM建模方法的基础上,采用均匀化方法建立考虑非规则颗粒细观边界特征的LSM-MT方法.通过与显式方法的计算结果对比,相对误差为0.03%~2.58%,与LSM模型计算结果相比,改进幅度为0.12%~2.30%,结果表明LSM-MT法可以有效考虑非规则颗粒细观边界特征. 3)所建立的PHF-LSM-MT方法实现了非均质岩石材料建模及水力裂缝传播过程模拟,通过与线弹性理论的起裂压力对比,得到隐式模型和改进模型的相对误差分别在8.98%~12.02%和8.94%~11.98%之间,且随包裹体含量的增加,模型起裂压力降低.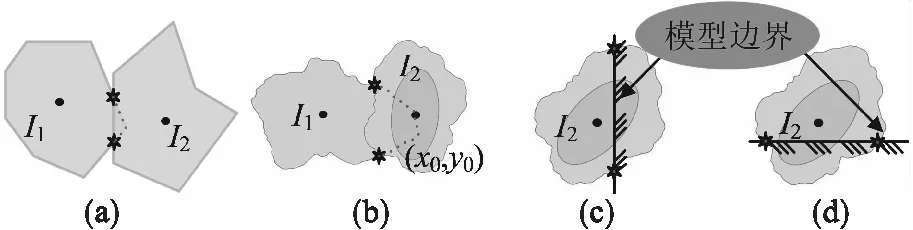
2.3 非规则颗粒间距计算
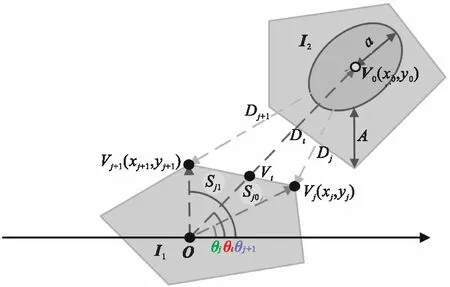

3 多尺度非规则边界有限元模型
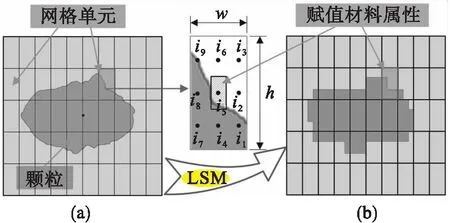
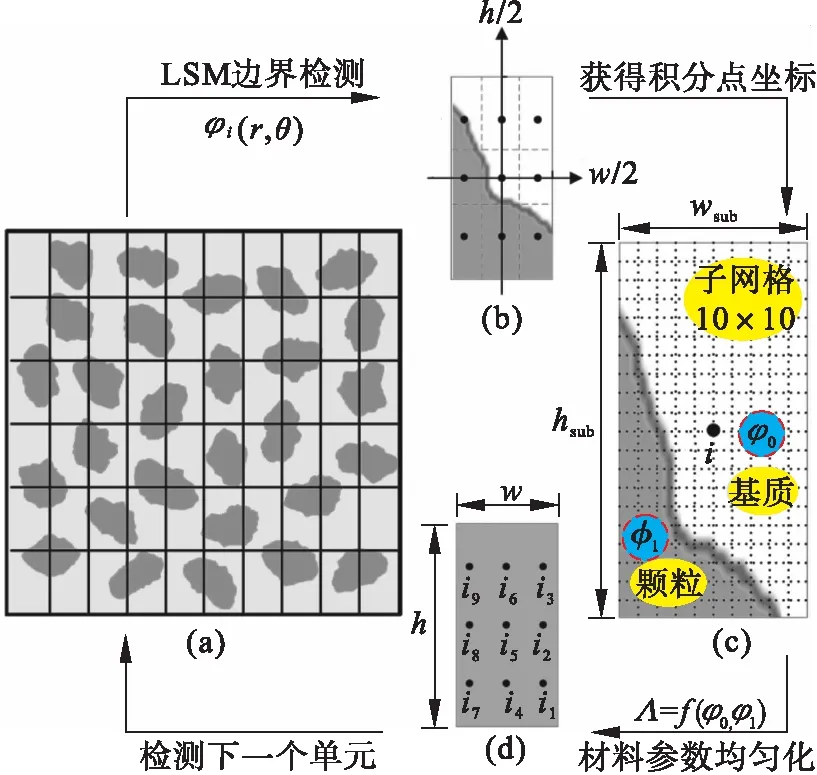
3.1 非均质岩石材料边界水平集方程及参数均匀化

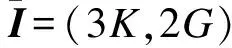


3.2 颗粒边界细观模型验证




4 非均质岩石的水力裂缝特性
4.1 PHF方法的控制方程

4.2 PHF-LSM-MT水力压裂数值计算模型

4.3 均质岩石材料水力裂缝扩展

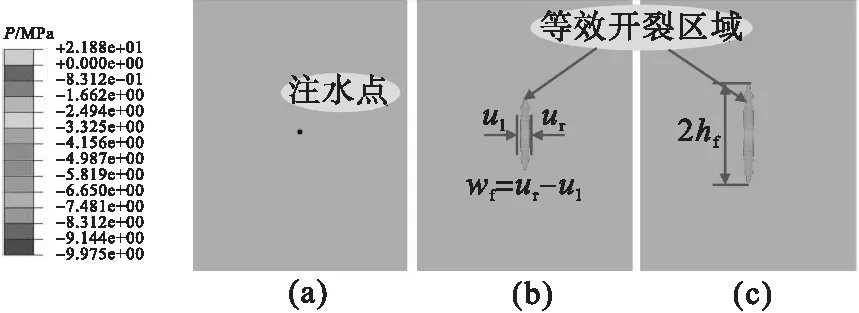
4.4 非均质岩石水力裂缝发展特性




5 结 论

