四轮轮毂电动汽车的紧急制动能效性转矩优化
李寿涛,孙鹏鹏,魏玉博,于丁力
(1.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022;2.吉林大学 通信工程学院,吉林 长春 130022;3.利物浦约翰摩尔大学 工程与技术学院,利物浦 L33AF)
近年来,由于全球自然资源短缺和环境污染问题越来越严重[1],新能源汽车已成为未来汽车工业发展的趋势.相较于传统汽车,四轮轮毂电动汽车的制动系统增加了电机制动,需要协调制动系统中的液压制动和电机制动,来提高制动的安全性和能效性[2-3].
车辆制动时的安全性能受到车轮滑移率的影响,车轮保持最佳滑移率可以有效地利用路面附着能力,避免失去方向控制,缩短制动距离.文献[4]研究了高低载频对逆变器的开关损耗以及对电动汽车滑移率控制性能的影响,提出了一种考虑低载频驱动的单速率PWM滑移率控制方法.文献[5]研究了电动客车上的复合制动系统,提出了计算总制动扭矩的性能指标和制动扭矩分配的优化策略.然而该策略未充分利用再生制动系统中轮毂电机回收能量的特性.文献[6]提出了纯电机独立实现制动的控制方法,该方法能够最大程度地回收能量.但电机制动工作区间有限,电机转矩可能出现饱和,这将影响制动安全.文献[7]采用一种基于预测的鲁棒控制器跟踪期望滑移率,通过转矩之间的合理分配提高了车辆在制动过程中的稳定性.文献[8]提出了基于模型预测控制的控制策略,保证车辆高再生效率和良好的制动性能.文献[9]为了前轮具有最佳滑移率和达到能量效率最大化,提出了一个修订的控制策略,但是在执行器约束范围内可能没有最优解.
针对以上问题,本文利用预测控制算法在线滚动优化特性[10],提出了一种新的四轮轮毂电动汽车紧急制动时转矩的优化控制方法,能快速响应跟踪车辆在不同路面附着条件下的最佳滑移率稳定区域.同时,显式处理了轮胎滑移率约束、电机输出转矩约束,合理分配制动转矩,保证车轮的最佳滑移率并提高能量回收效率.在不同路面条件下的仿真研究分析,证明了控制方法的适应性和有效性.
1 系统模型
设计控制器的控制对象为四轮轮毂电动汽车,车轮可以独立控制,其制动时车轮左右性能可以认定是相同的.四轮轮毂电动汽车四分之一车辆纵向模型如图1所示[11].
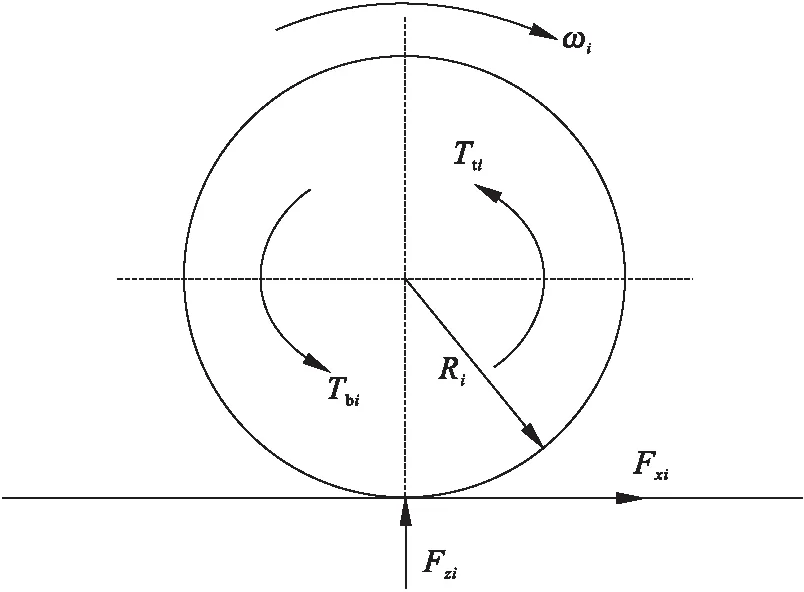
图1 四分之一车辆纵向模型简图
由牛顿第二定律和力矩平衡分析可得
(1)
其中:m为分配到每个车轮上的质量;vx为车辆纵向速度;fa为分配到每个车轮上的空气阻力;Ji为转动惯量;ωi为车轮旋转角速度;Tbi为制动力矩;Tti为驱动力矩;Ri为有效滚动半径;Fxi为轮胎纵向力;i=f,r分别为前、后车轮.
施加到每个车轮空气阻力fa为
(2)
其中:f是空气阻力系数;Fa为车轮空气阻力.
车轮在滚动过程包括滚动和滑动两个状态.滑移率为滑动状态所占的比例:
(3)
关于路面附着系数与滑移率之间的非线性关系,常用模型为Burckhardt轮胎模型:
μ(λ)=C1(1-e-C2λ)-C3λ.
(4)
式中,C1,C2,C3是轮胎模型的参数.
同时,轮胎纵向力可以表示为
Fxi=μ(λ)Fzi.
(5)
其中,轮胎垂直载荷Fzi是影响轮胎特性的重要因素,具体公式:
(6)
式中:lf,lr分别为质心到前后轴的距离;g是重力加速度;h是质心的高度;M为整车质量.
2 基于预测控制的转矩优化控制算法
控制系统的整体结构如图2所示,控制器将四轮轮毂电动汽车的车轮滑移率控制到最佳稳定区域,保证车辆行驶安全的前提下尽可能提高制动能量的回收能力.
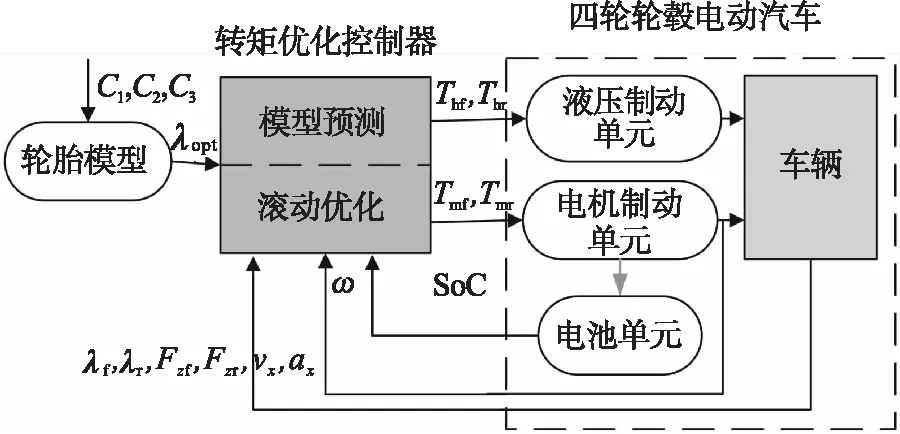
图2 滑移率控制系统结构图
2.1 基于状态空间的预测模型
本文研究的控制主要目标是紧急制动时滑移率的控制.对动态方程(3)求导可得
(7)
将式(1)代入可得
(8)
选取状态方程中状态变量是当前时刻的滑移率,控制量包括前后轮的液压制动力矩和电机制动力矩.在直线行驶的工况下车辆的左右性能可以认定是相同的.
(9)
当控制器的采样时间为Ts,运行时间为t,则当前时刻可以被描述为
k=(int)t/Ts.
(10)
将车辆模型(1)离散化后转化为
(11)
其系统动态模型(2)~(6)表示为
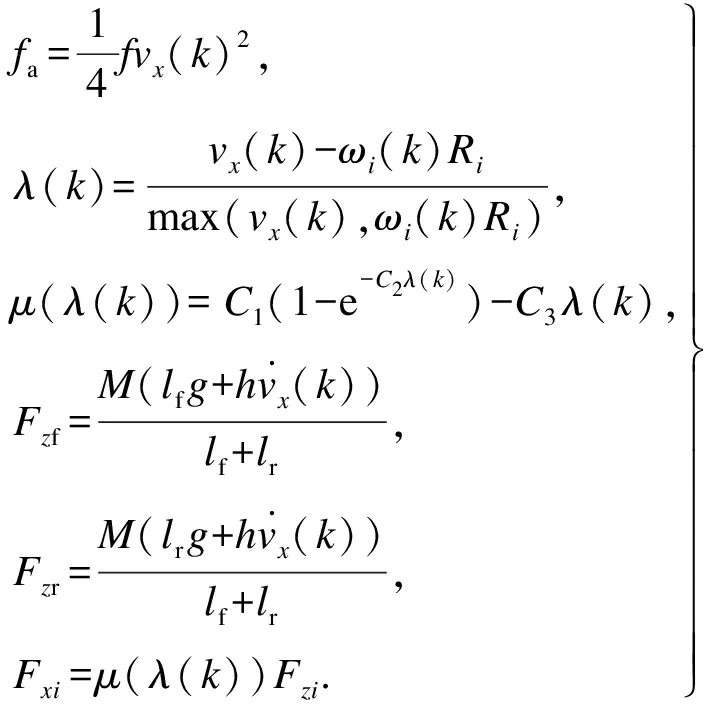
(12)
将当前k时刻测量的状态值作为初始状态,预测未来k+1到k+p的时刻,表示为k+1|k,k+2|k,…,k+p|k,则预测时域p内未来时刻的状态变量为
x(k+p-1|k)=x(k+p-1|k)+
f(x(k+p-1|k),u(k+p-1|k))Ts.
(13)
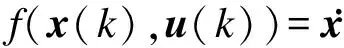
由式(11)可得,车辆在预测时域内选取滑移率作为跟踪项:
(14)
2.2 转矩优化控制模型
本文所提出的控制优化的目标函数考虑车辆对最佳滑移率的跟踪效果、控制量变化幅度和能量回收大小,其目标是车轮的滑移率准确跟踪期望值并提高能量回收能力.
转矩优化控制器的目标是车轮滑移率准确跟踪期望值,令优化模型的序列R(k+1)为
(15)
由此设计目标函数J1:
J1=‖ϑY(Y(k+i|k)-R(k+i))‖2=
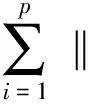
2(λopt(k+i))‖2.
(16)
其中,ϑY为加权因子.考虑制动过程中的平顺性,由此设计目标函数J2:
J2=‖ϑU(ΔU(k))‖2=
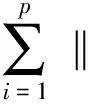
Thr(k+i|k)+Tmr(k+i|k)-
(Thf(k+i-1|k)+Tmf(k+i-1|k)+
Thr(k+i-1|k)+Tmr(k+i-1|k))‖2.
(17)
其中,ϑU为目标函数J2的加权因子.
在制动转矩优化过程中,为了提高再生制动的能量回收能力,设计目标函数J3:
J3=‖ϑE(-E(k))‖2.
(18)
其中:E(k)表示在预测过程中回收的能量;ϑE为目标函数J3的加权因子.
在预测控制每次实施控制信号,控制量相应动态地进行滚动优化,因此对于复杂的优化目标需要在不改变其趋势的情况下进行近似,提高算法实时性.本文简化转矩优化问题中的能量回收,将其转化为

Thr(k+i|k)-Tmr(k+i|k))‖2.
(19)
由以上分析可得车辆转矩优化控制的优化问题为
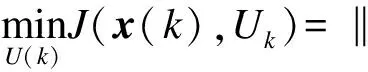
(20)
(21)
其中:Thmax是液压制动器允许的最大输出;ωimax是电机允许的最大转速;Tmmax是电机允许的最大输出,其具体值根据轮毂电机的外特性的数据建立哈希表得到;SoC为剩余电量.
在系统的预测控制的每一步根据系统更新状态,求解优化问题(20)和(21).将优化所得的最优解首个序列施加到系统上,施加到被控对象之后滚动优化,进行到下一时刻的控制过程.
3 仿真实验及结果分析
本文基于Carsim和Matlab/Simulink设计了联合仿真平台.四轮轮毂电动汽车的主要参数如表1所示.分别在湿沥青和冰雪路面条件下进行仿真分析.
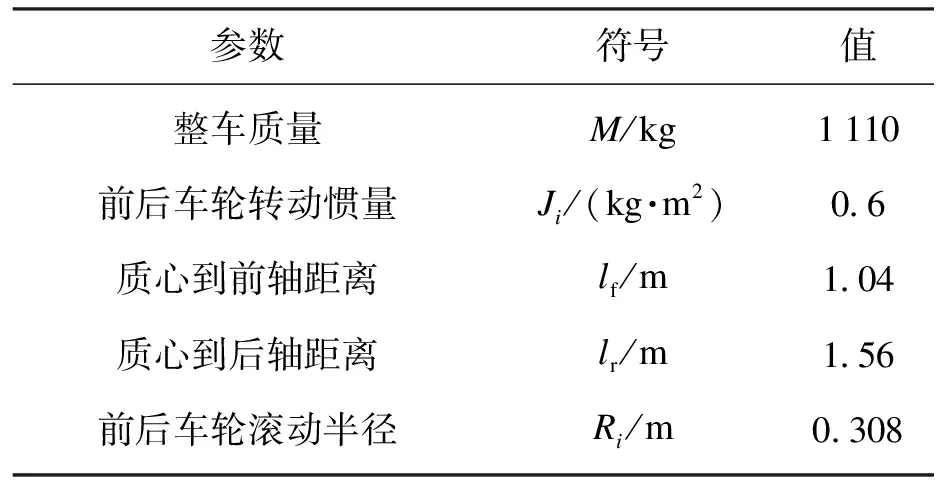
表1 四轮轮毂电动汽车的参数
3.1 在湿沥青路面条件下的仿真实验
设置湿沥青路面的仿真工况,其中车辆初始速度为60 km/h.基于路面附着条件得到最佳滑移率为0.13,通过与未使用控制的对比结果来验证,仿真结果如图3所示.
图3a,图3b表明,本文转矩优化控制策略能在0.23 s内有效地跟踪最佳滑移率稳定区域.此外由图3e表明,本文的控制策略在保证车辆不发生抱死的情况下,车辆的减速加速度更大,相同时间内制动距离为26.76 m,与未施加控制的制动距离36.49 m相比,减少了9.73 m.同时图3c~图3f表明了控制策略保证了各电机转矩处于约束内,同时提高了能量回收能力,其最终电池SoC为80.08%.
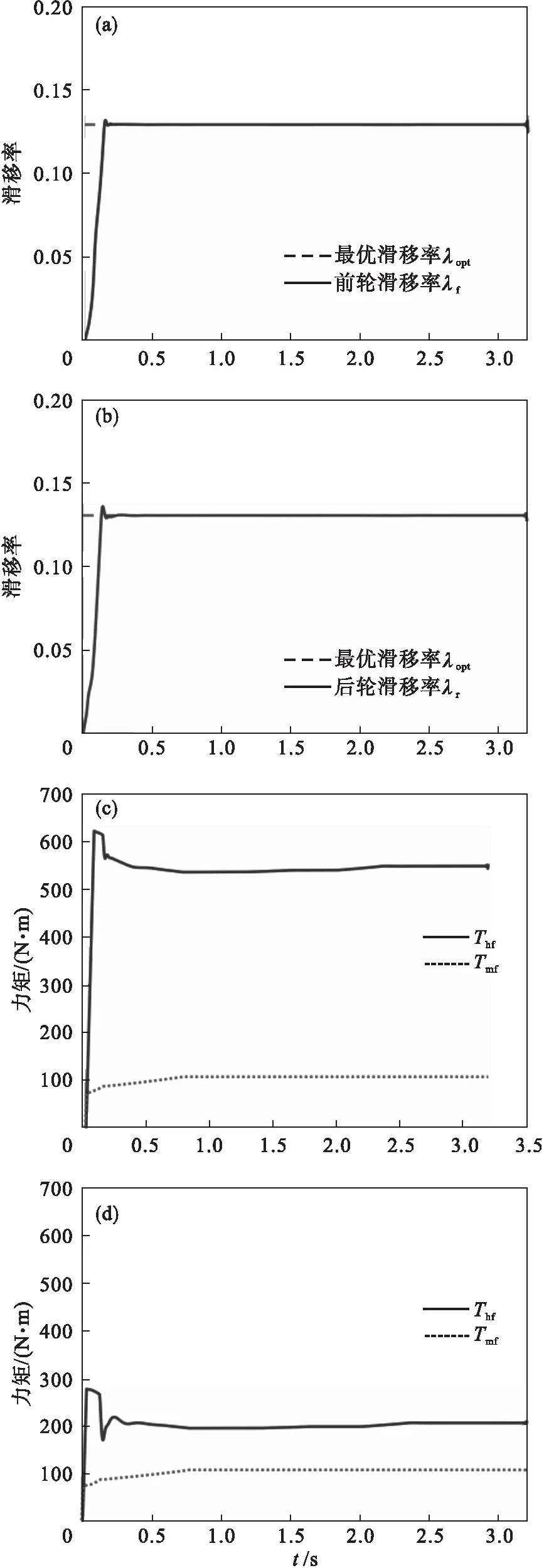
图3 湿沥青路面条件下的仿真结果
3.2 在冰雪路面条件下的仿真实验
设置冰雪路面的仿真工况,其中车辆初始速度为40 km/h.基于路面附着条件得到最佳滑移率为0.05,通过与未使用控制的对比结果来验证,仿真结果如图4所示.
仿真结果表明,当路面附着条件变差,本文转矩优化分配可以使控制对象的滑移率在0.27 s内跟踪到最佳滑移率的稳定区域内.本文的控制策略在保证车辆不发生抱死的情况下,制动距离为31.13 m,未控制的制动距离为32.96 m,减少了1.83 m.此外由图4c~图4f可知,转矩优化分配策略保证了电机转矩处于约束内,同时也提高了能量回收能力,其最终电池SoC为81.10%.
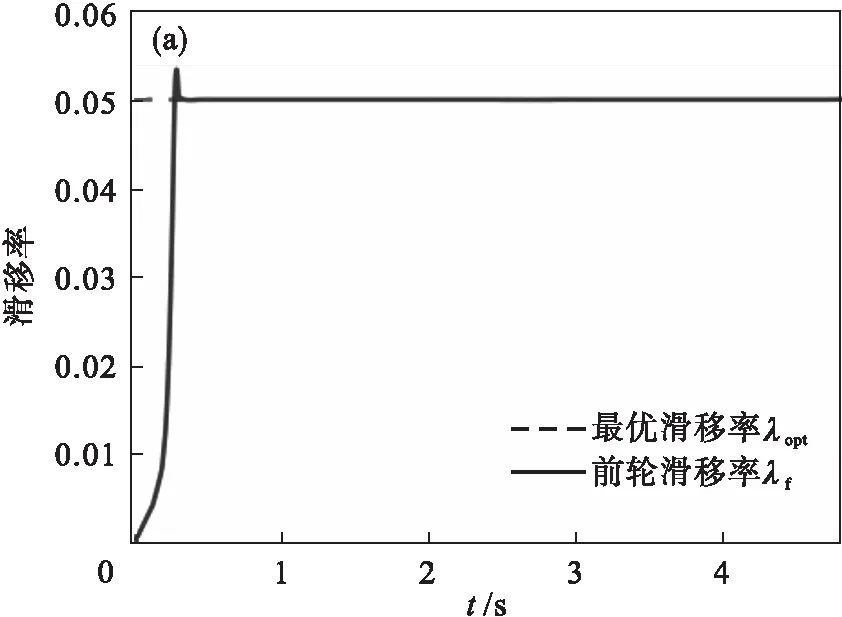
图4 冰雪路面条件下的仿真结果
4 结 语
本文针对四轮轮毂电动汽车紧急制动工况,提出一种基于预测控制的转矩滚动优化算法.通过显式处理不同条件下的电机转矩约束,解决了电机转矩出现过饱和的问题.并在优化模型中引入能量回收项,通过调整优化目标函数中跟踪项与能效优化项的权重,在车辆的制动性和能量回收效率的能效性之间寻求满意解.仿真结果验证了所提出控制器的有效性,即保证跟踪轮胎最佳滑移率,防止出现车轮抱死的前提下,提高了系统的能量回收能力.下一步将考虑模型的不确定性以及外部扰动对控制性能的影响和低附着路面条件下的算法优化.

