Y型网式过滤器多目标优化正交试验

喻黎明 曹东亮 李久霖 李 娜 韩 栋 邵社刚

(1.昆明理工大学现代农业工程学院， 昆明 650500； 2.农业农村部工程建设服务中心， 北京 100081； 3.交通运输部公路科学研究院， 北京 100088)

0 引言

当前我国农业快速发展的过程中，微灌技术的应用在农业发展中起到重要的作用[1-2]。网式过滤器作为微灌系统中的核心设备，有效减少杂质进入，提高灌水质量，进而减缓微灌系统堵塞。网式过滤器[3-4]具有结构简单、便于制造与安装、过滤效果好和价格低廉等优点，在国内外微灌系统中被广泛使用。

为了提高网式过滤器的综合性能，国内外学者进行了大量研究，并取得了一定成果。目前，对网式过滤器的优化研究主要集中在过滤机理和结构上。在过滤机理优化方面，李曼等[5-6]研究了不同过流量和含沙量对水头损失的影响，并得到了浑水水头损失计算公式；朱德兰等[7]进行Y型网式过滤器堵塞试验，得到局部水头损失与肥液浓度、滤网清洁度的关系式；喻黎明等[8]通过CFD-DEM耦合模拟了不同流量下Y型网式过滤器内部不同粒径沙粒的运动与分布，分析了过滤器内部流态对沙粒运动分布的影响；宗全利等[9]进行堵塞试验，建立了滤网内外压降与滤网孔径、滤网厚度等的定量关系式。在结构优化方面，李盛宝等[10-11]将3种不同目数的滤网集成在同一壳体，提高了过滤效果；陶洪飞等[12]探究了不同出水管角度对网式过滤器内部流场的影响；王新坤等[13]通过优化过滤器滤筒形状、出入水口夹角和位置等结构改善过滤器内部流场分布，提高了速度分布的均匀性；WU等[14]提出在过滤器结构设计中应选择合适的进出口直径和滤网直径以改良过滤器的水力性能；王柏林等[15]将旋流过滤器和网式过滤器串联连接进行试验，分析其在不同含砂率条件下的过滤性能变化规律；周理强等[16]通过内置导流片改变了过滤器内部流态和沙粒运动分布规律，提高了过流能力与抗堵塞能力。

目前结构优化研究可分为将不同的过滤器或者部件进行组合和改变单个结构参数而固定其他结构参数，而涉及同时改变两个或者多个参数的研究较少。因此，本文对网式过滤器同时配置4个结构参数进行正交试验，以分析多个结构参数同时改变对多目标的影响，从而系统地筛选出最佳结构参数组合，并分析结构优化对过滤器过滤性能的影响机制，为过滤器优化设计提供理论依据。

1 正交试验设计与方法

1.1 网式过滤器结构

本文研究模型为农田灌溉常用Y型网式过滤器，过滤器主要由进水口、筒体、滤芯、堵头以及出水口组成(图1)，其中滤芯由冲孔钢板和不锈钢滤网复合而成，滤网包覆在冲孔钢板内侧。冲孔钢板可使滤网避免因流量大而产生移位，不锈钢滤网则起到过滤泥沙杂质的作用。

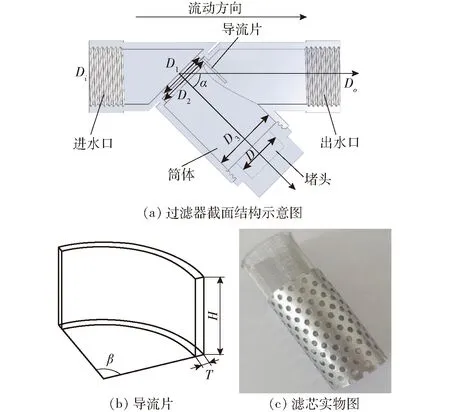
图1 Y型网式过滤器内部结构图Fig.1 Schematics of Y-type screen filter structure

1.2 试验因素和试验方案

如图1所示，网式过滤器结构参数主要有滤网目数N=60、入口直径Di=24 mm、出口直径Do=24 mm、出口与筒体间夹角(以下简称夹角)α=45°、入口处最小内径D1=20 mm、滤网内径D2=26 mm、筒体内径D3=29.5 mm、导流片圆心角β=60°、导流片高度H=15 mm、导流片厚度T=2 mm、堵头高度h=10 mm、堵头直径D=20 mm。结合周理强等[16]和喻黎明等[17]提出的过滤器结构优化方案建议，正交试验最终选择夹角α、入口缩小比R(D1与D2的比值)、导流片圆心角β以及导流片高度H共4种因素作为研究对象。每种因素选取3个水平，因素水平如表1所示。通过CFD-DEM耦合计算，探讨不同因素对过滤器整体性能影响的规律，从而找到因素影响的显著性大小顺序和最优参数组合。

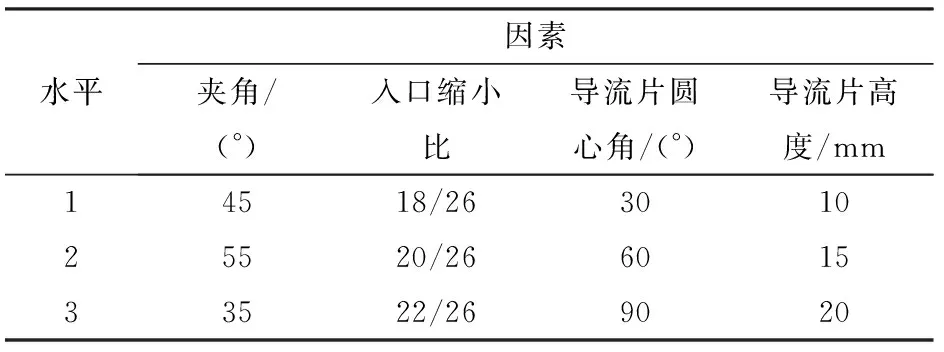
表1 正交试验因素水平Tab.1 Factors and levels of orthogonal test

1.3 综合评分法

进行多指标正交试验时，需要采用综合评分法进行分析[18-20]。根据各个指标的重要程度，对每个试验的每个指标按一定的评分标准评出分数，再将同一个试验中各指标的分数求和即为该试验的总分数。将这个总分数作为这个试验的总指标，然后根据这个总指标(分数)，利用单指标试验结果的直观分析法作进一步的分析，确定较好的试验方案。

对每个试验的各个指标按照指标隶属度计算标准评出分数，指标隶属度计算方法如下：

若试验指标越高越好，则

(1)

式中η′——中速过流量区域面积占比隶属度

ηi——第i个试验中速过流量区域面积占比

ηmax——正交试验中最大中速过流量区域面积占比

ηmin——正交试验中最小中速过流量区域面积占比

(2)

式中I′r——拦截率隶属度

Iri——第i个试验拦截率

Irmax——正交试验中最大拦截率

Irmin——正交试验中最小拦截率

若试验指标越低越好，则

(3)

式中H′L——水头损失隶属度

HLi——第i个试验水头损失，m

HLmax——正交试验中最大水头损失，m

HLmin——正交试验中最小水头损失，m

(4)

式中S′r——颗粒分布相对标准偏差隶属度

Sri——第i个试验颗粒分布相对标准偏差

Srmax——正交试验中最大颗粒分布相对标准偏差

Srmin——正交试验中最小颗粒分布相对标准偏差

1.4 网格划分与边界条件

根据表1要求，采用SolidWorks绘制过滤器三维模型。利用软件ICEM(The integrated computer engineering and manufacturing code)对模型进行网格划分，主要为了将空间连续的流体区域分割成足够小的计算域，然后在每个计算区域上应用流体控制方程，求解所有区域的流体计算方程，最终获得整个计算区域上的物理量分布。网式过滤器的计算域形状较为规则，因此采用六面体结构化网格，同时将出入口的相贯线区域网格加密，网格质量采用Determinant 3×3×3标准度量并且都在0.5以上。网格数量越多，理论上计算精度越高，但是会增加计算量，因此需要对网格进行无关性验证[21-22]。将网格模型edge上的节点数依次扩大1.0倍(方案1)、1.2倍(方案2)、1.4倍(方案3)、1.6倍(方案4)，对各网格模型进行水力性能测试，选取验证工况流量Q=3.2 m3/h，以水头损失为评价指标，与Q工况对应的水头损失H0为6 m。

根据数值计算得到的水头损失和对应的试验水头损失，定义相对误差r为

(5)

式中HL——计算水头损失，m

当r小于1%，该网格被认为满足计算要求，r越小，说明网格对计算结果的影响越小。由表2可以看出，方案1和方案2的网格可满足计算要求，方案3和方案4中存在不满足计算要求的试验。综上所述，采用方案1进行正交试验。

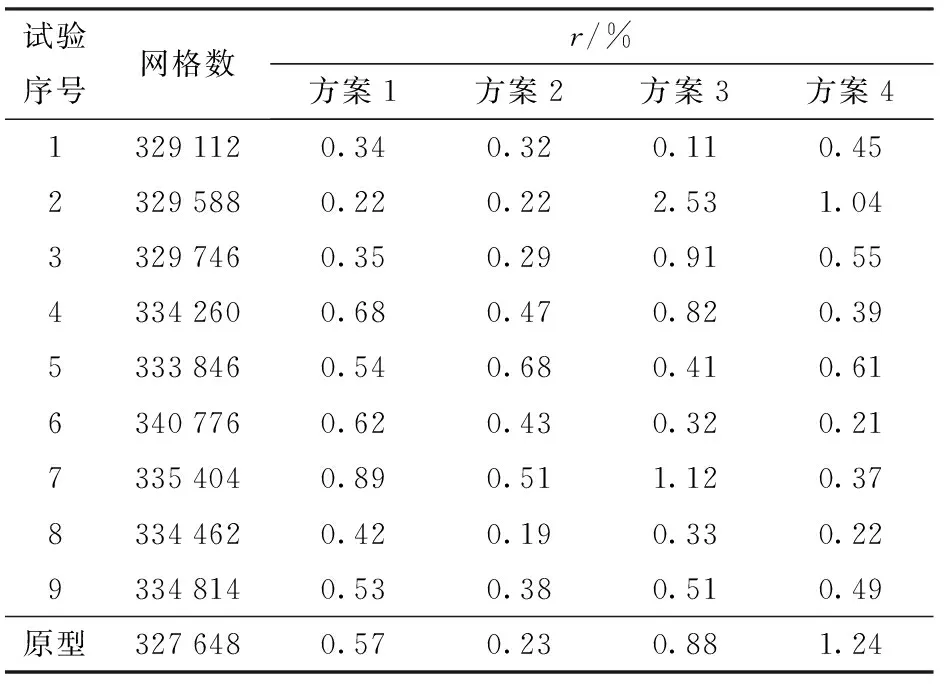
表2 正交试验组网格数Tab.2 Grid number of original model and orthogonal test

液相属于低速不可压缩流动，因此选用压力基求解器。过滤器内部存在回流与射流现象，故采用标准k-ε模型[23]对网式过滤器三维流场进行求解，近壁区采用标准壁面函数。流体介质为液态水，固体介质为abs塑料。进口边界条件采用速度入口，流体与离散相均采用相同的速度(0.5 m/s)，流速方向与入口边界垂直，湍流强度I为5%，入口水力直径为24 mm，出口采用压力出口，回流强度选取默认值。应用SIMPLE算法来耦合压力和速度之间的关系，收敛残差为10-3，时间步长为1×10-4s。

本文水沙两相流的计算中颗粒相体积分数小于10%，所以选用拉格朗日模型。颗粒设置为球形颗粒，采用3种粒径颗粒，半径分别为100、150、200 μm。颗粒与壳体的物性参数、接触参数设置如表3、4所示。

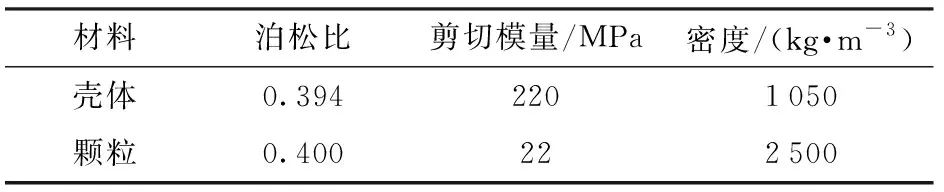
表3 物性参数Tab.3 Physical parameters

表4 接触参数Tab.4 Contact parameters

1.5 数值模拟验证

在清水条件下，通过试验测量的手段求解网式过滤器过流量与水头损失之间的关系式并与数值模拟的拟合结果进行对比，以验证数值模拟结论的准确性。清水为实验室自来水，试验装置如图2所示。

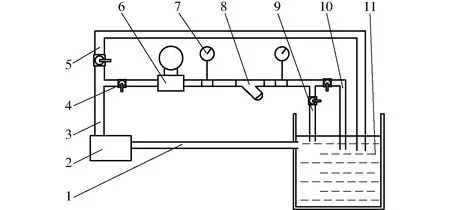
图2 清水试验装置示意图Fig.2 Schematic of clear water test device1.进水管 2.自吸泵 3.出水管 4.球阀 5.分压管 6.智能电磁流量计 7.压力表 8.Y型网式过滤器 9.取水口 10.回流管 11.蓄水桶

物理试验过程中，通过调节进口处阀门使网式过滤器前端压力表分别在0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10 MPa下稳定运行，此时网式过滤器两端的压力表读数之差换算后即为网式过滤器的水头损失。记录10组不同水头损失下过滤器的过流量，经拟合得到过滤器的流量-压差曲线。数值模拟过程中，入口流速依次选定为0.5、1.0、1.5、2.0、2.5 m/s，从而得到不同入口流量，入口与出口的压力差都可以通过Fluent在REPORT模块中计算得出。

网式过滤器的流量-压降[24]关系式为

Δh=kQx

(6)

式中 Δh——进出口之间的水头损失，m

k——水头损失系数

x——流态指数

根据式(6)对所获得的数据点拟合得到如图3所示的流量-压降曲线。

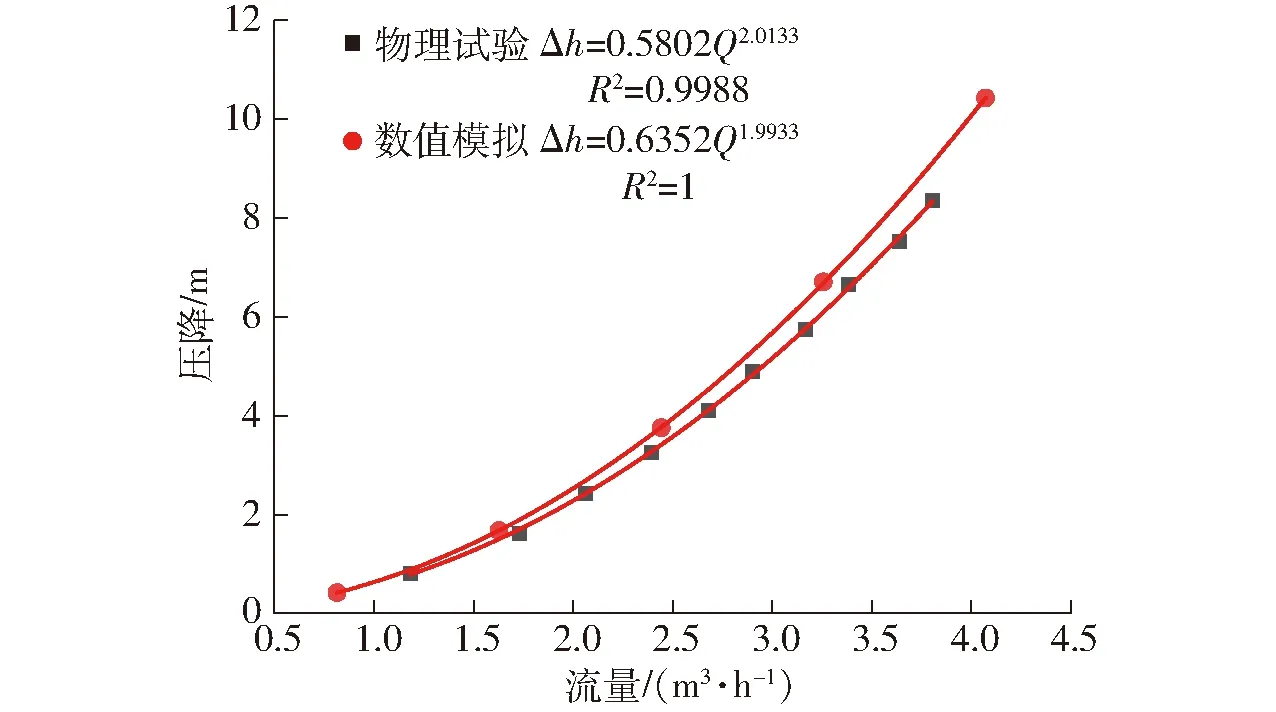
图3 清水状态下的流量-压降曲线Fig.3 Flow-pressure drop curves under clear water condition

对比物理试验和数值模拟拟合公式，两者的水头损失系数与流态指数差异分别为8.65%、1.03%。物理试验与数值模拟拟合公式的决定系数分别为0.998 8和1，表明式(6)对流量与压降关系的解释度很高，通过t检验法对结果进行验证，得到两组数据的压力差异不显著，证明了数值模拟结果是可靠的。对比不同流量下，仿真计算值与实际测量值的相对误差分别为8.32%、14.75%、9.01%、9.98%、9.36%、7.61%、9.11%、7.65%、9.36%、8.18%，即多数误差在10%以内，满足定量预测要求，也证明了仿真计算结果的准确性，因此可以采用数值模拟的方法对过滤器性能进行分析和结构参数优化。

2 结果与分析

2.1 正交试验水力性能分析

2.1.1水头损失

水力性能作为衡量过滤器性能的重要指标，即在相同的入口速度条件下，进出口之间水头损失之差越小，说明过滤器的水力性能越好。根据正交试验方案，以同样的数值计算方法依次计算在流速0.5、1.0、1.5、2.0、2.5 m/s下水头损失，然后对流量与压降数据点进行曲线拟合，9组试验均遵循流量-压降曲线变化规律。图4曲线可以清晰地分为3个层次，试验4、5、6(夹角均为55°)水头损失系数普遍较大，试验7、8、9(夹角均为35°)水头损失系数较小，指数总体波动不大，所以对于水头损失而言，夹角的影响最为明显。

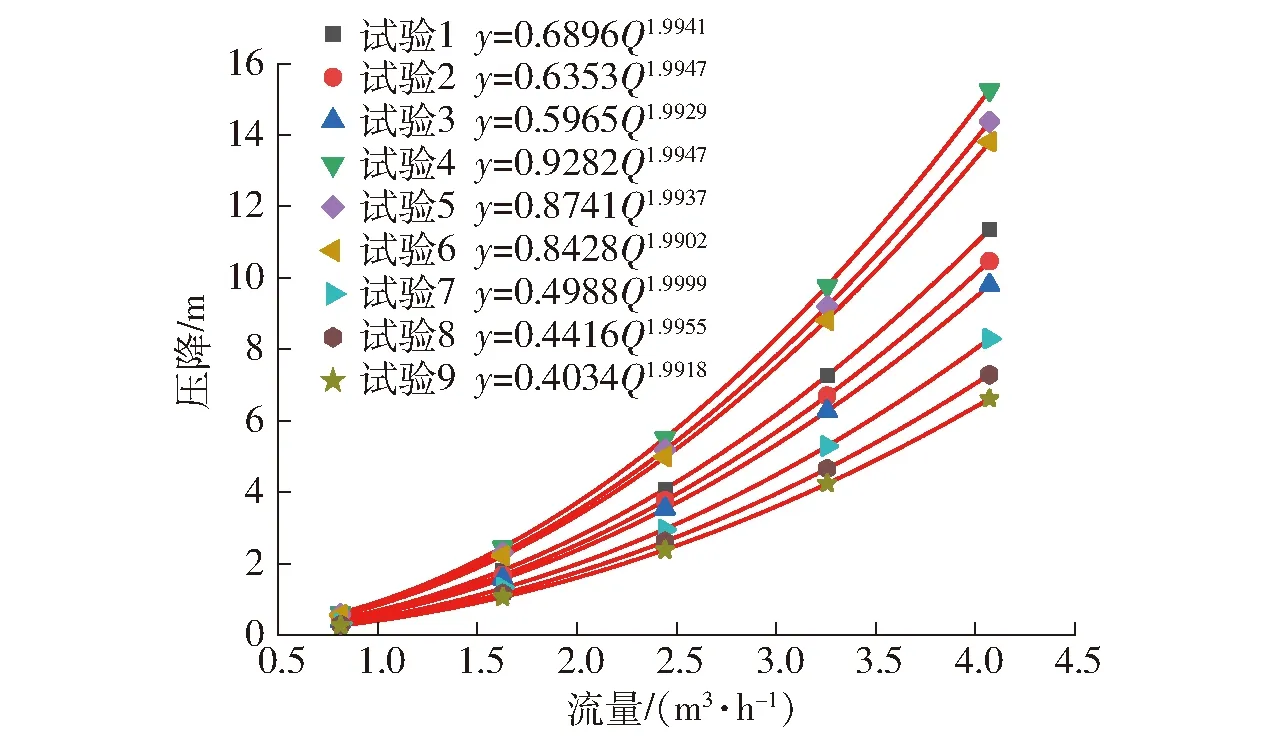
图4 正交试验清水状态下的流量-压降曲线Fig.4 Flow-pressure drop curves of orthogonal test under clear water condition

以流速0.5 m/s为例，对水头损失HL进行单指标直观分析，极差分析如表5所示，各因素对水头损失影响的显著性由大到小依次为夹角、入口缩小比、导流片高度、导流片圆心角。Ki(i分别取1、2、3)代表每个因素中与i水平相关的试验结果之和，ki代表每个因素中与i水平的试验结果之和的平均值。夹角为主导因素，导流片圆心角及高度敏感度较小，该结果与图4相吻合。夹角为55°时，水头损失均值为0.585 m；夹角为35°时，水头损失均值较55°减小了49.1%，随着夹角的增大，水头损失也在增大，这与弋鹏飞等[25]得出的弯折角越大，局部水头损失也越大的结论一致。

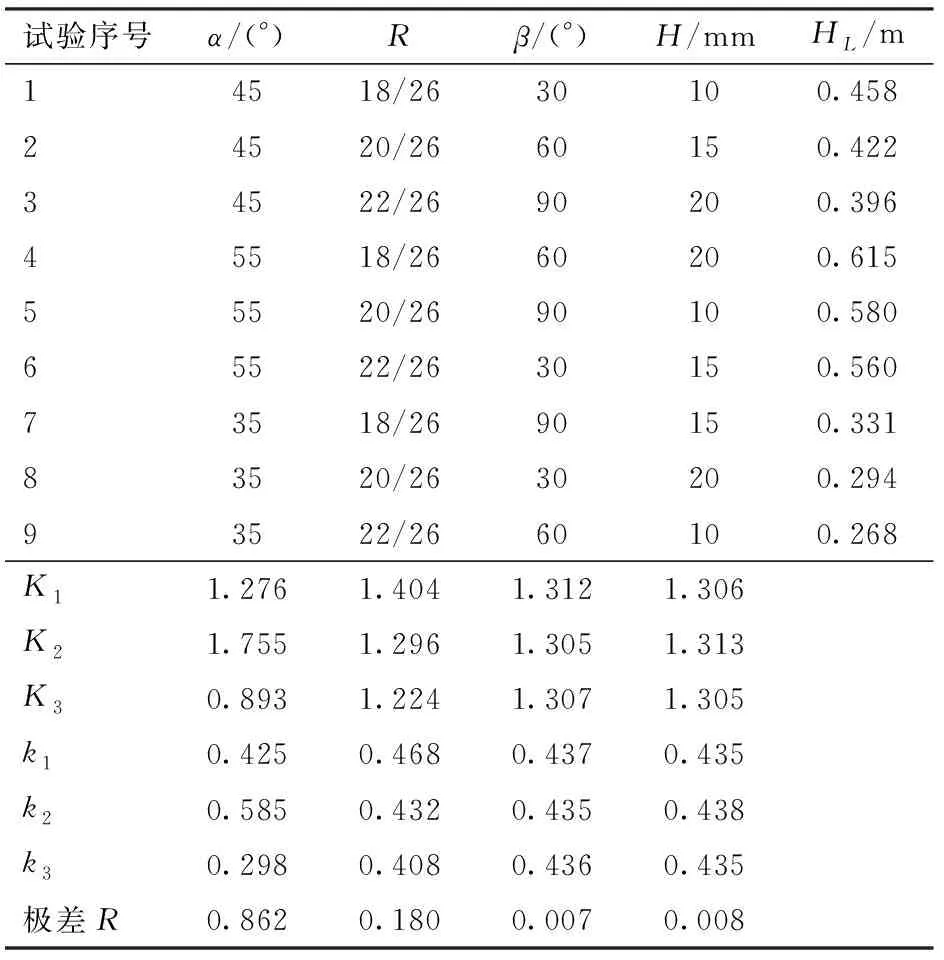
表5 水头损失极差分析Tab.5 Range analysis of head loss

2.1.2网面过流量

网面过流量也是反映过滤器性能的重要指标，对于网式过滤器而言，仅保证水头损失小不足以说明过滤器结构设计的合理性，网面整体的使用效率也需要考虑。

考虑本次试验采用的滤芯为滤网和钢板复合而成，钢板冲孔之外的区域过流量为零。首先根据冲孔数将滤网面划分为200个区域，并设置对应的检测面，通过CFD计算流速0.5 m/s下过滤器的内部流场，将每个区域过流量数据导至Excel，最后统计每个滤网面的总过流量，作为衡量滤网面过流能力的指标。由于过流量区域分布在圆柱型滤网上，为方便观察使用Surfer软件将网面过流量以柱面展开云图的形式表达。

如图5a所示，滤芯相邻圆周上的冲孔交错，相隔圆周上的冲孔处于同一列，所以图5a中的点A对应图1c中滤芯第一圆周上任意冲孔的圆心，图5a中的点B即为与点A同处一列最末一圆周上对应冲孔的圆心。云图以滤网出口侧点A作为坐标原点，X轴坐标值表示为沿圆周到点A的弧长，沿滤网从点A指向点B为Y轴正方向。将不同区域的网面总过流量与对应的位置坐标进行整合，得到图5b的过流量分布云图。以试验1云图为例，距Y轴20 mm的区域称为出口侧，其余区域称为入口侧；Y轴0～10 mm区域称为上端，10～30 mm称为中端，30～40 mm称为下端。

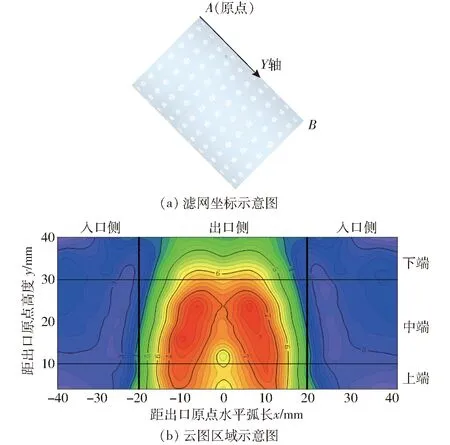
图5 云图坐标和区域示意图Fig.5 Schematics of cloud map coordinates and region

将云图按照过流量划分为低速、中速、高速3种过流区域类型，分别对应流量2～4 L/h、4～6 L/h、6～9 L/h。根据云图(图6)可以发现，所有试验的中高速过流量区域都集中在出口侧圆柱面上，而入口侧过流量在2～4 L/h范围内。试验1～6出口侧的下端区域存在低速过流量，出口侧过流量分布梯度较大，而试验7、8、9出口侧中高速过流量区域面积更广且分布更为均匀。

图6 正交试验网面过流量分布云图Fig.6 Cloud maps of network flow distribution in orthogonal test

正交试验最大最小过流量统计如图7所示，各试验中最大过流量波动幅度最大为2.45 L/h；最小过流量几乎处于同一水平，最大值与最小值只相差0.51 L/h。各试验最大最小过流量间倍数分别为3.43、3.34、3.51、3.54、3.89、4.17、2.68、2.88、3.01。整体而言，试验7、8、9间倍数较小，试验4、5、6倍数偏大，前者倍数的均值较后者减小26.1%，表明试验7、8、9的过流量梯度过渡更为平缓即过流量分布更加均匀。

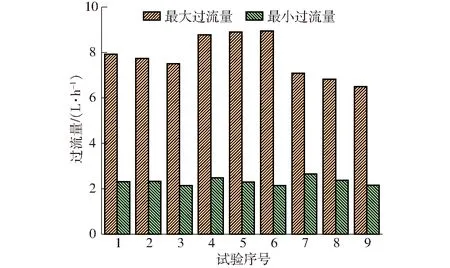
图7 正交试验滤网最大、最小过流量Fig.7 Maximum and minimum overflow of filter screen in orthogonal test

不同速度的过流量区域面积占比统计如图8所示，试验6低速过流量区域面积最大，为1 983.35 mm2，占滤网面面积的59.9%。试验7、8、9的中速过流量区域面积占比高于其他试验10个百分点左右，而低、高过流量区域面积都小于其他试验。对于网面过流量而言，结构优化的目的就是减小局部低、高过流量区域的面积，提高中速过流量区域面积，缓和过流量之间的梯度。总体而言，试验7、8、9的过流量分布更加均匀，其高速过流量区域面积占比较低，使滤网承载过小的水流压力，不易使滤网发生变形而影响最终过滤的效果；低速过流量区域面积在试验组中保持低水平，能使滤网得到充分利用和保证过滤效率。

图8 正交试验3种过流速度过流量区域面积占比Fig.8 Area proportion of three kinds of overcurrent velocity in orthogonal test

将图8中速过流量区域面积占比η作为评价指标，分别计算得到正交试验组的中速过流量区域面积占比，用极差分析法进行分析，从而得到各因素对指标η的影响程度。由表6可知，对中速过流量区域面积占比而言，影响因素的主次顺序为夹角、导流片圆心角、导流片高度和入口缩小比。其中，夹角的极差远大于其他因素，所以夹角对中速过流量区域面积占比作用最大，当夹角由55°减小至35°时，中速过流量区域面积占比提高了57.63%。

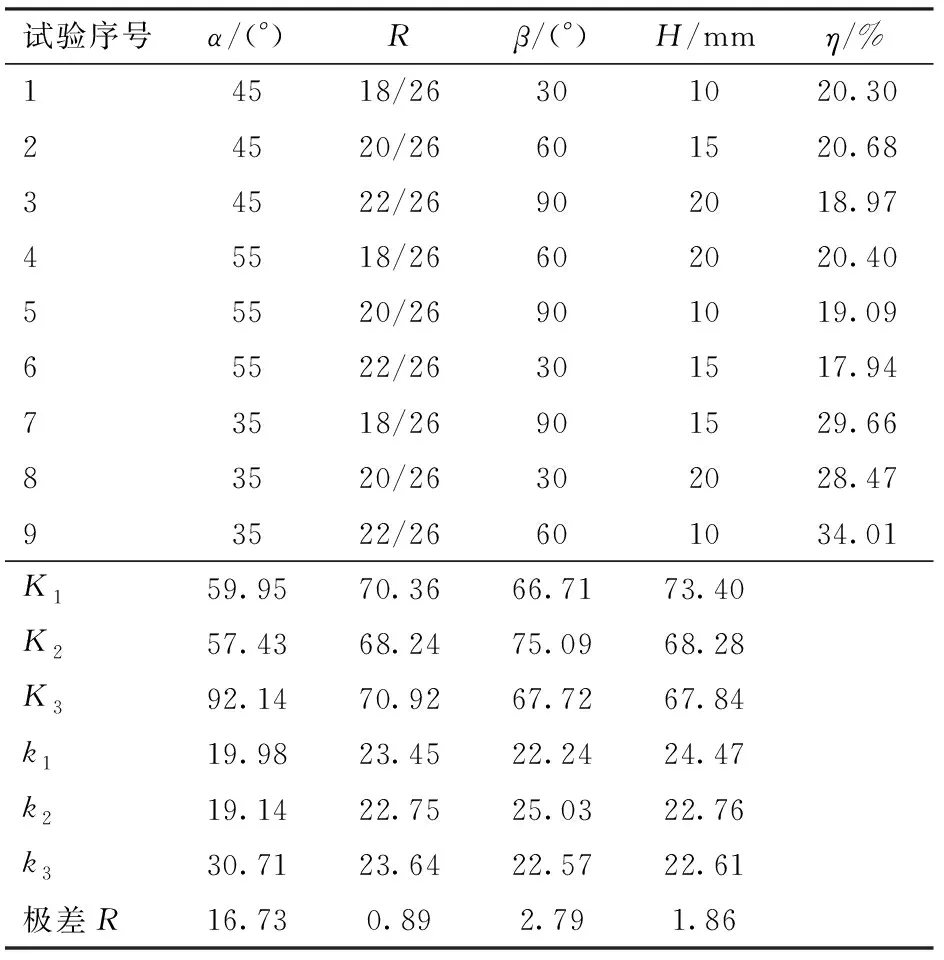
表6 中速过流量区域面积占比极差分析Tab.6 Range analysis of area proportion of medium speed flow area

2.2 正交试验抗堵塞性能

2.2.1颗粒通过点均匀度

在过滤的初始阶段，部分小颗粒能够通过滤网孔而不被拦截。随着过程的进行，颗粒在滤网上逐步堆积，从而形成滤饼层。分布均匀的颗粒会形成均匀的滤饼，起到辅助过滤的效果，同时也能避免由于局部堵塞而产生的一系列问题，因此需要通过分析小颗粒的运动轨迹来研究滤饼的分布。为了研究颗粒通过点分布的均匀性，采取类似网面过流量云图的区域划分方法，统计落在不同区域上的通过点，并采用相对标准偏差作为衡量坐标分布均匀性的指标，相对标准偏差Sr计算公式为

(7)

式中M——区域数

zi——区域i内颗粒数

在CFD-DEM计算结果的基础上通过Matlab统计颗粒轨迹线，计算小颗粒通过滤网面所对应的坐标(通过点坐标)，并使用Matlab计算其Sr，Sr越小表明通过点分布越均匀。

图9为Matlab绘制的颗粒通过点分布图，可以发现正交试验通过点主要集中在出口侧上端以及出口侧和入口侧交汇的柱面区域。对比网面过流量图，可以发现颗粒通过率低区域与高、低速过流量区域相对应，颗粒集中通过区域与中速过流量区域相对应。究其原因，高速过流量区域颗粒很容易堆积，形成滤饼从而对小颗粒进行拦截；高流速导致频繁碰撞，颗粒通过率下降；低速过流量区域水流流速过小以至于颗粒的跟随性低，颗粒的无规则运动明显。

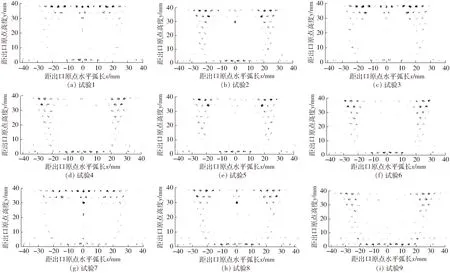
图9 正交试验颗粒通过点分布图Fig.9 Distributions of particles passing through points in orthogonal test

由表7可知，影响颗粒通过点分布相对标准偏差Sr主导因素为入口缩小比，影响因素的敏感度由大到小为入口缩小比、夹角、导流片圆心角、导流片高度。在9组试验中R取22/26时，Sr分别为45.67、58.20、41.61，其均值较R为18/26、20/26分别减小45.4%、12.1%，这也表明入口缩小比越大，颗粒分布均匀度越佳。

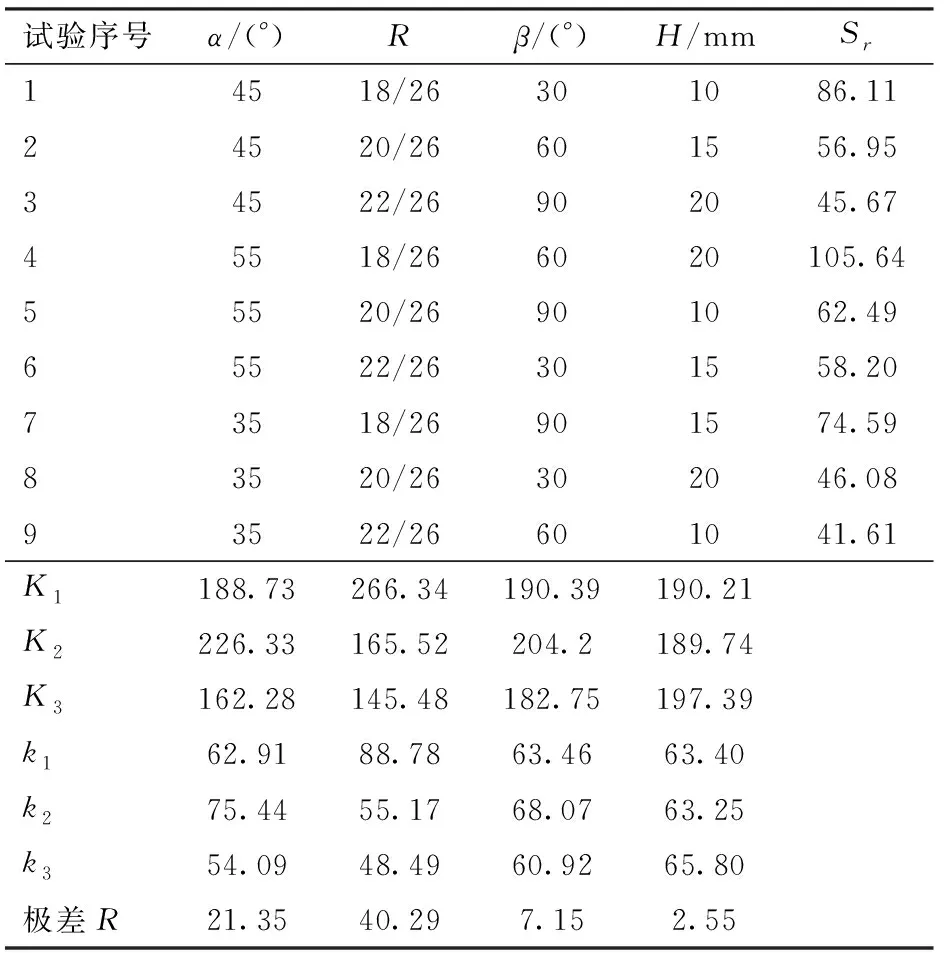
表7 颗粒通过点分布相对标准偏差极差分析Tab.7 Range analysis of relative standard deviation of particle passing point distribution

2.2.2颗粒拦截率

颗粒进入过滤器的结果分为通过和拦截两种情况，本次试验投入3种颗粒各2 000个，粒径分别为200、300、400 μm，滤网的筛分使粒径为300 μm和400 μm的颗粒被拦截，被拦截的颗粒分布在滤网的各个区域并构成滤饼的主体结构。滤饼层有助于捕获粒径小于过滤精度的颗粒，从而提高拦截率。通过Matlab计算出未通过滤网的200 μm颗粒数，然后将拦截数量除以总颗粒数得出拦截率Ir，并对正交试验的拦截率进行极差分析，结果如表8所示。

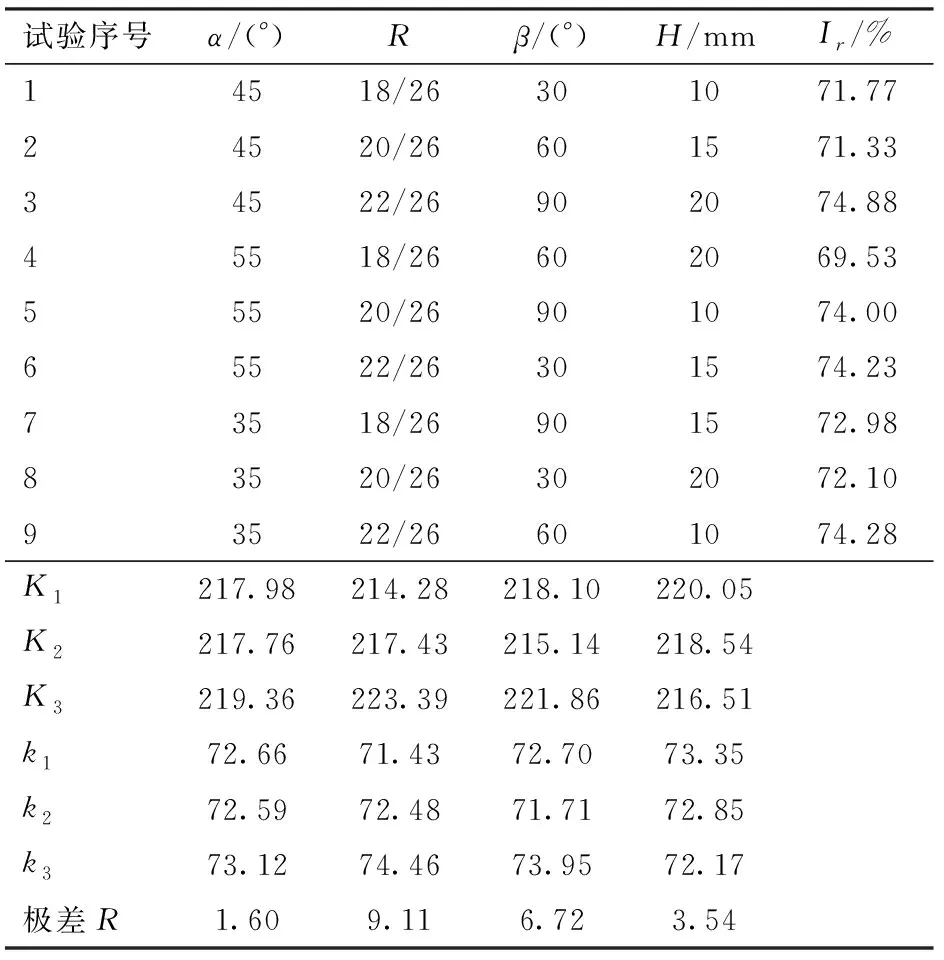
表8 拦截率极差分析Tab.8 Range analysis of interception rate

试验3拦截200 μm颗粒数最多达到493个，效果最差的为试验4拦截172个。各因素对拦截率影响由大到小依次为入口缩小比、导流片圆心角、导流片高度、夹角。各因素影响水平相近，入口缩小比为主导因素，夹角敏感度较小。当入口缩小比取22/26时，3组拦截率的均值为74.46%，较R为18/26提高近3个百分点。

2.3 参数优化与试验验证

2.3.1参数优化

本文试验指标选取4个，属于多指标正交试验，因此采用综合评分法对结果进行分析。视各指标的重要性相同，所以各指标的权重都为0.25。4个指标的隶属度由式(1)～(4)计算得出，将各指标隶属度之和作为整个试验的总指标。利用单指标试验的直观分析，得出影响因素对总指标敏感度从大到小依次为夹角、入口缩小比、导流片高度、导流片圆心角。根据极差分析(表9)得到最优因素组合为：夹角35°、入口缩小比22/26、导流片高度 10 mm、导流片圆心角90°。

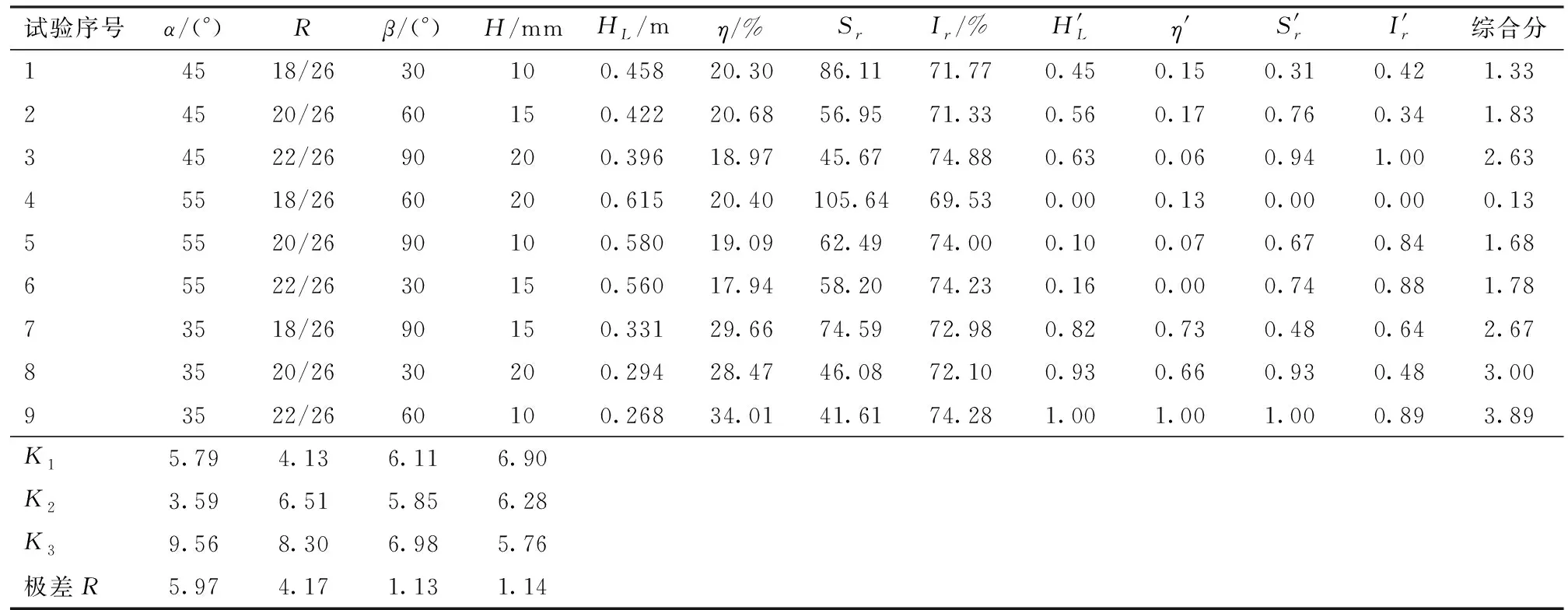
表9 综合评分法对试验结果的极差分析Tab.9 Range analysis of test results by comprehensive scoring method

2.3.2优化方案试验验证与分析

根据正交试验分析得出的最优设计参数组合重新构建几何模型，通过数值模拟对优化方案模型进行性能试验，将得到的结果与原模型试验值进行对比分析。

当入口流速为0.5 m/s时，优化方案水头损失为0.268 m，与原模型相比降低了36.6%。从两者网面过流量图(图10)来看，原型过滤器的最大过流量为7.74 L/h，最小过流量为2.32 L/h；优化模型最大过流量为6.49 L/h, 最小过流量为2.26 L/h。最大最小过流量间倍数由3.34下降为2.87，表明不同区域之间过流量变化更为平滑，不存在陡增与突降现象。低速过流量区域面积占比由55.7%降低到53.7%，虽然面积占比只减小2个百分点，但是图10a低速区域大部分位于2～3 L/h范围内，而图10b 低速区域过流量接近中速过流量，前者平均过流量远小于后者。图10a中速过流量区域面积占比20.68%，图10b中速过流量区域面积占比36.45%。同改进前相比，中速过流量区域面积占比增加15.77个百分点。

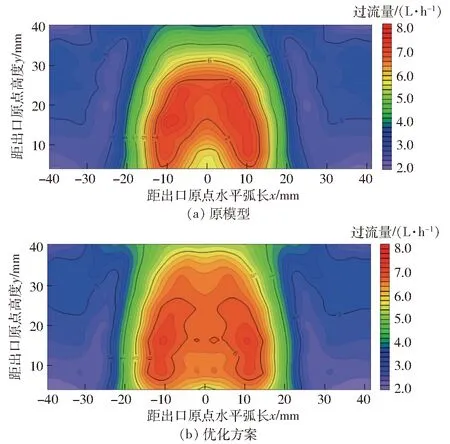
图10 原模型和优化方案网面过流量对比Fig.10 Comparison of network flow between original model and optimization scheme

由图11可知，图11a通过点颗粒主要集中在出口侧上端以及出口侧与入口侧的交汇处，而图11b颗粒分布范围广，滤网大部分区域都被充分利用。改进前Sr为57.56，颗粒拦截率为71.42%；优化改进后Sr为32.66，拦截率为75.35%，同改进前相比，相对标准偏差减小43.26%，拦截率提高3.93个百分点，表明了优化方案的有效性，也说明优化参数的准确性和可行性。

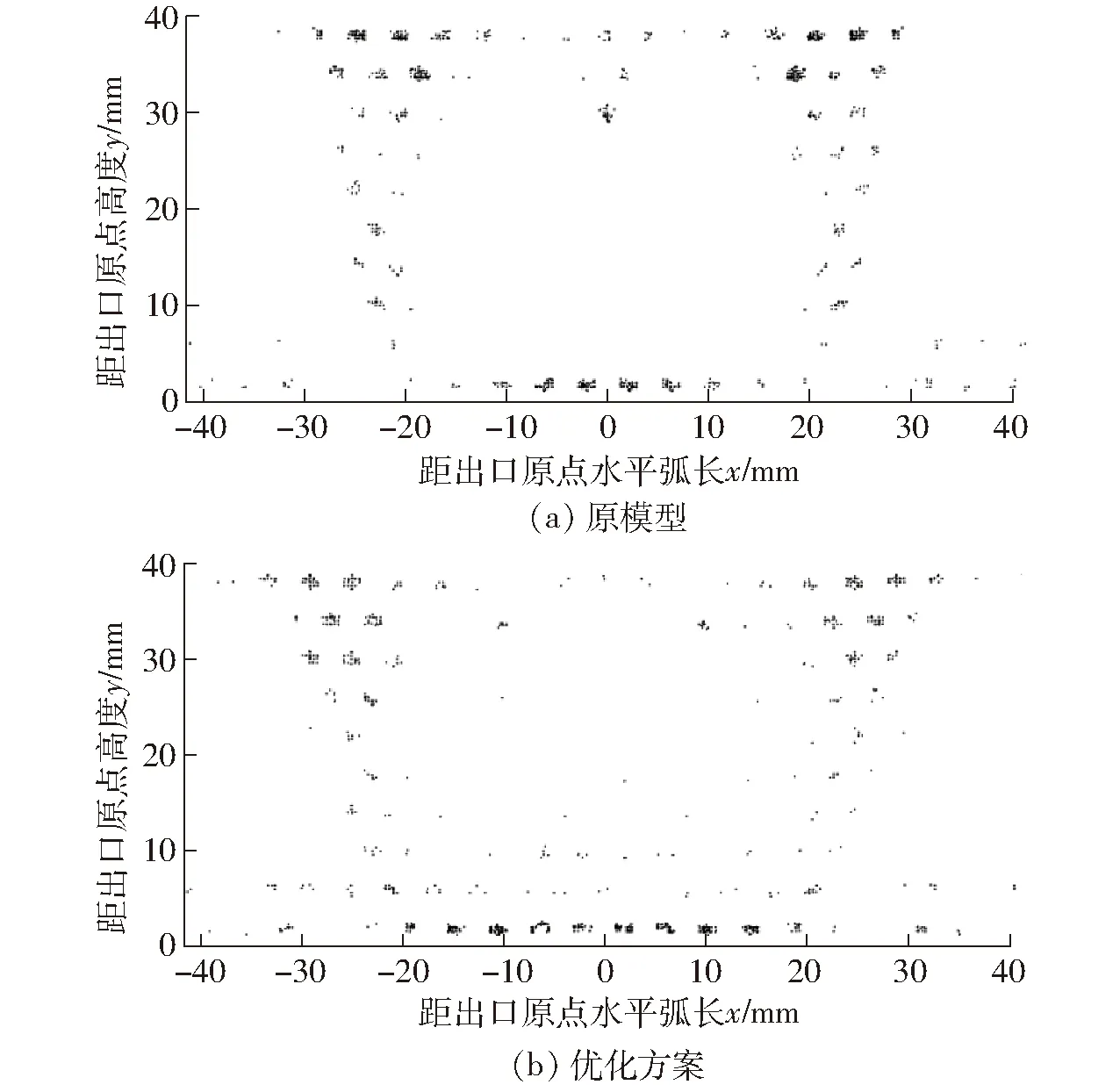
图11 原模型和优化方案颗粒通过点分布对比Fig.11 Comparison of particle distribution between original model and optimization scheme

3 讨论

通过结果分析发现影响水力性能最显著的指标为夹角，影响抗堵塞性能最显著的是入口缩小比，而对总指标而言，因素敏感度最大的为夹角，入口缩小比次之，并且夹角和入口缩小比的极差都远大于导流片圆心角和高度。极差较大的因素，表明了因素的水平对试验结果影响较大，所以夹角和入口缩小比为主要因素。在Y型网式过滤器优化的过程中，首先考虑夹角，因为夹角的确定对水头损失和网面过流量影响最大，同时水力性能与颗粒运动存在密切联系。对比图6与图9可以发现，颗粒集中区域都在最大最小过流量位置附近，改变最大最小过流量位置或者降低最大过流量与提高最小过流量对抗堵塞性能也有很大提升，进而体现结构优化对过滤器过滤性能的影响。

夹角的确定其实也意味着筒体与出口管道接触面积(即出口截面积)的确定，夹角越小，出口截面积越大。对于水头损失和中速过流量区域面积占比两个指标而言，夹角为主要影响因素且夹角与两指标呈正相关性，即随着夹角的减小，出口截面积逐步增大，更多的水流通过滤网之后直接进入出口管道，避免因与筒体的碰撞而导致水头损失的增大，同时降低与壁面撞击的回流对即将通过冲孔以及滤网内部的水流产生冲击的可能性。碰撞以及冲击发生的机率减小也提高了各个区域过流速度，中速过流量区域面积占比也将随之变大，所以夹角变小可以有效增大出水面面积，这与张凯等[26]将过滤器出口段改变为前大后小的圆弧形状，改善过滤器过滤性能的原理类似。

过滤器网面最大过流量与最小过流量所对应位置如表10所示，由于过滤器为对称结构，所以过流量基本遵循关于Y轴对称。降低最大过流量与提高最小过流量，能够保障滤网的正常工作，提高滤网上各个区域的平均流速和颗粒的网面分布度。根据表10中的坐标可以看出，有7组试验的最大过流量位置处于(±10.34 mm,16 mm)，局部过高的过流量易使滤网发生变形，宗全利等[9]发现过流量大的区域更容易分布泥沙从而产生局部堵塞，导致水头损失上升过快，进一步降低系统的整体过滤性能。为降低确定位置的局部过高过流量，建议：①考虑改变导流片形状，将高过流量区域的网孔遮挡住，避免第一波水流冲击此位置网孔。水流通过狭窄的入口形成高速射流，经导流片对流速进行削弱从而达到降低过流量的效果。②减小高过流量区域冲孔半径的同时，增加冲孔的密度，达到过流面积保持不变而降低过流量的目的。最低过流量集中发生在(±37.23 mm,4 mm)，网面过流量图(图10)显示低过流量区域都处于滤网的入口侧，采取以下两个措施来提高入口侧滤网的利用率：①考虑在靠近入口侧再设置一块或者多块导流片，对水流流态进行调整，使得部分水流向着出口侧前进，并在出口侧的导流片作用下进行流动，另一部分直接在新置导流片作用下通过入口侧的滤网。②因为入口侧过流量较小，所以可以增大入口侧滤网的冲孔半径，这不仅增加了入口侧总过滤面积，也不会出现因过流量过大而产生滤网变形甚至破损的现象。

表10 最大、最小过流量对应位置坐标Tab.10 Corresponding location coordinates of maximum and minimum overflows

本文正交试验虽然很好地平衡了试验次数，能够找到影响各指标的主导因素以及最佳参数组合，但未考虑各因素间交互作用对试验指标的影响，建议可以采用通径分析[27]作进一步分析。因为通径分析不但能够量化因素对指标产生影响的敏感度，还能分析因素的间接作用是拮抗作用还是协同作用，而在本试验中极差分析只能得到夹角对水头损失影响最为显著，入口缩小比次之，导流片圆心角及高度敏感度较小，不能探究当出口与滤网间夹角为主导因素时，另外3种因素对水头损失的间接作用是拮抗还是协同。通径分析可以根据误差对结果的通径系数的绝对值来判别是否存在对结果影响较大的因素未被考虑进去，使得结构优化方案更加严谨。

4 结论

(1)从水力性能来看，出口与筒体间夹角为主导因素。正交试验中、高速过流量区域均集中在出口侧，而入口侧过流量停留在2～4 L/h范围内。当夹角越小时，出口截面积与其呈正相关，中速过流量区域面积随之变大，使得过滤器内流场分布更为均匀。

(2)对抗堵塞性能而言，入口缩小比的影响最为显著。根据网面过流量与通过点分布云图，发现颗粒通过率低区域与高、低速过流量区域相对应，颗粒集中通过区域与中速过流量区域相对应。入口缩小比越大，颗粒分布均匀度越佳，拦截率也呈现正向增长。

(3)本文试验属于多目标正交试验，采用综合评分法确定了最优参数组合：出口与筒体间夹角35°、入口缩小比22/26、导流片高度10 mm、导流片圆心角90°。其中夹角对综合指标影响最为显著，因此夹角是网式过滤器性能优化设计的一个关键参数。优化后，水头损失与相对标准偏差分别减小了36.6%、43.26%，拦截率与中速过流量区域面积占比分别提高3.93、15.77个百分点，表明了优化方案的可行性和实际应用价值。