基于平稳小波变换的输电线路故障测距

吴承阳， 王玲桃

(山西大学 电力工程系，山西 太原 030013)

0 引 言

电力输电线路是电力系统能量传输的重要途径。当输电线路发生故障后，如果不能准确地确定故障点位置并及时排除故障，随着运行时间的增长，就会造成故障范围的进一步扩大，造成系统的过电压，损坏正常运行的线路和电气设备，从而破坏系统的安全运行[1]，造成不可挽回的经济损失。因此，为了最大限度地减少故障对输电线路的影响，及时准确地故障定位和故障排除，在国内外有着非常重要的研究意义、经济效益以及广泛的应用前景[2]。

现有的故障测距方法主要有故障分析法、行波法和智能法。故障分析法具有稳定性好、经济性好的优势，但是测距精度有限，并且计算量很大[3]。行波法具有快速高效的特点，且不受线路参数、故障电阻和故障类型的影响，但存在准确识别波头困难的问题[4]。人工智能技术在数据处理方面有较强的优势，但存在小样本问题和计算效率低的问题。

目前，在实际的电力系统应用中，行波测距是进行故障定位的主要方法。但是，行波的波速会受到自然环境的影响，因此波速的准确测量非常困难[5]。行波在传输过程中会发生衰减，导致行波波头的突变点越来越弱，难以准确辨别故障行波传输至线路两侧的具体时刻[6]。因此，行波法的可靠性和精度有待进一步提高。针对以上问题，本文提出一种基于平稳小波变换的双端输电线路行波故障测距方法。该方法通过将故障行波信号进行相模变换和平稳小波变换分析，最后得出行波波头到达两端测量点的时刻，由此实现故障定位。用MATLAB进行仿真试验，并与离散小波变换的方法进行比较，最终得出本文方法具有更高的准确性。

1 故障测距的理论依据及模型

1.1 不受波速影响的双端行波测距法

双端行波法是通过测量故障行波波头到达两侧测量点的时间进而实现故障定位。与单端行波法相比，双端行波法不用考虑行波复杂的折反射，测距精度更高[7]。

双端行波测距模型如图1所示。

图1 双端行波测距模型

图1中：设线路总长为L，假设在F点处t0时刻发生故障，设故障点距离测量端M、N的距离分别为lM和lN，故障行波首次到达两侧测量端的时间分别为tM1和tN1，第二次到达两侧测量端的时间分别为tM2和tN2，设故障行波波速为v。则有：

(1)

当故障点的位置距离测量端M近时，M端接收到的前两次行波信号分别为第一次到达的故障行波和它在故障点处的反射波。此时由以上公式消去波速可得故障点距M端的距离为：

(2)

当故障点的位置距离测量端N近时，则选用N端接收到的前两次行波信号进行测距计算，同理可得：

(3)

使用该测距方法计算故障距离不受行波波速的影响，只需要测出故障行波到达两侧测量端的时间。

1.2 平稳小波变换

平稳小波变换是由离散小波变换进一步优化而来的，它是一种非正交小波变换。在变换过程中，平稳小波变换不进行向下采样，具有平移不变性，这样就使得变换后的逼近信号和细节信号与原信号长度相等，因此可以最大程度地保留原信号中的有用信息[8]。

用平稳小波变换进行降噪处理，可以有效削弱分解过程中的振荡效应，最终使得去噪后的信号更加平滑。因此，相较于离散小波变换，平稳小波变换在信号处理和奇异点检测方面具有更大的优势。

设一维信号f∈L2(R),其对应的二进制连续小波变换公式为：

(4)

当b=k2j时，式(4)为正交小波变换;当b=k时，则为平稳小波变换。

两种变换的分解算法如下：

Mallat算法：

(5)

à trous算法：

(6)

式中:h和g分别为小波分解的低通滤波器和高通滤波器;aj-1,k为尺度系数，反映逼近信号；dj-1,k为小波系数，反映细节信号。由以上公式可以看出，à trous算法与Mallat算法结构相同，但à trous算法由于其平移不变性保留

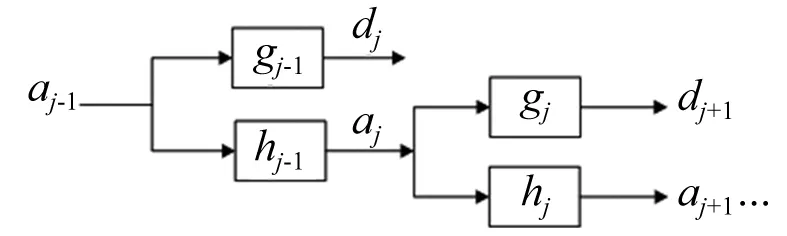
图2 平稳小波变换分解图

了更多原信号中的有用信息，因此更易于检测奇异点。

平稳小波变换的分解过程如图2所示。

1.3 基于SWT的双端法故障测距

由于三相线路存在电磁耦合，影响测距的精确性，为了便于分析，故障行波信号必须先通过相模变换解耦转化为相互独立的线分量。本文采用Clarke变换对行波分量进行解耦。Clarke变换矩阵为:

(7)

式中:iα、iβ、i0分别为电流行波的α模分量、β模分量和0模分量；ia、ib、ic分别为ABC三相电流。由于零模分量存在较为严重的衰减，而线模分量受外界影响因素小，因此本文选用α模分量进行故障定位。

将相模变换后的α模分量进行SWT分析，然后将分析结果代入到测距公式，便可得到测距结果。测距流程如图3所示。

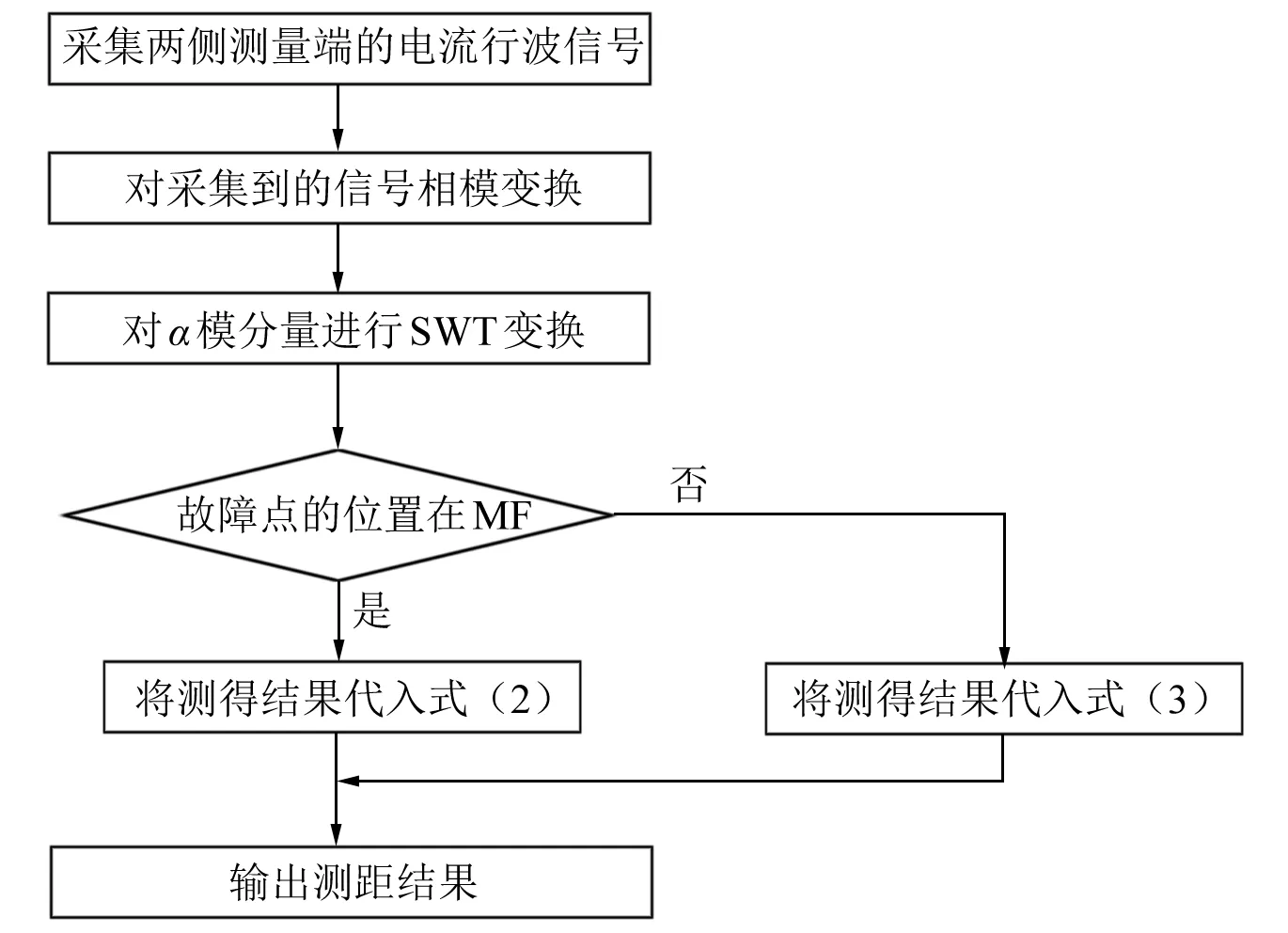
图3 故障定位流程图

2 仿真分析

通过MATLAB的电力系统工具箱建立了一个线路长度为300 km，电压等级500 kV，工频50 Hz的双电源供电系统。线路参数如表1所示。

表1 输电线路参数

本次仿真以A 相发生接地故障为例，仿真时长设为0.1 s，设置故障发生的位置为距M侧测量点100 km 处，对仿真模型中的三相故障发生器进行参数设置，故障发生时间为0.035 s，故障切除时间为0.083 s。

此时在测量端M和N测得的信号波形如图4所示。

用Clarke变换对故障行波信号进行解耦得到M、N两侧电流行波的α模分量。

设定采样率为10 000 Hz，并加入信噪比为0.000 1的白噪声，使用离散小波变换对电流α模分量进行db5的三层分解，并取第3 500到3 819的320个点分析，波形图如图5所示。

同样条件下，使用平稳小波变换对电流α模分量进行处理的结果如图6所示。

图4 A相接地故障时M、N两端的电流信号

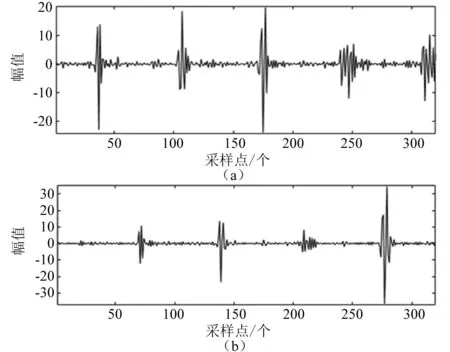
图5 M、N两侧电流行波离散小波变换波形

图6 M、N两侧电流行波平稳小波变换波形

比较图5、图6可以看出，通过平稳小波变换处理后的变换波形奇异点更加明显，因此更容易捕捉行波波头，相比较离散小波变换更加准确可靠。

由图6可以得到故障暂态行波首次和第二次到达测量端M的采样数值n分别为34、102，以及首次到达测量端N的采样数值68。通过测得的采样点的值，便可得到故障行波到达测量端M、N所对应的时刻分别为tM1=0.035 34 s，tM2=0.036 02 s，tN1=0.035 68 s，代入式(2)得故障距离为lM=100 km，误差为0 km。

在不同故障情况下进行仿真，测得的结果如表2所示。

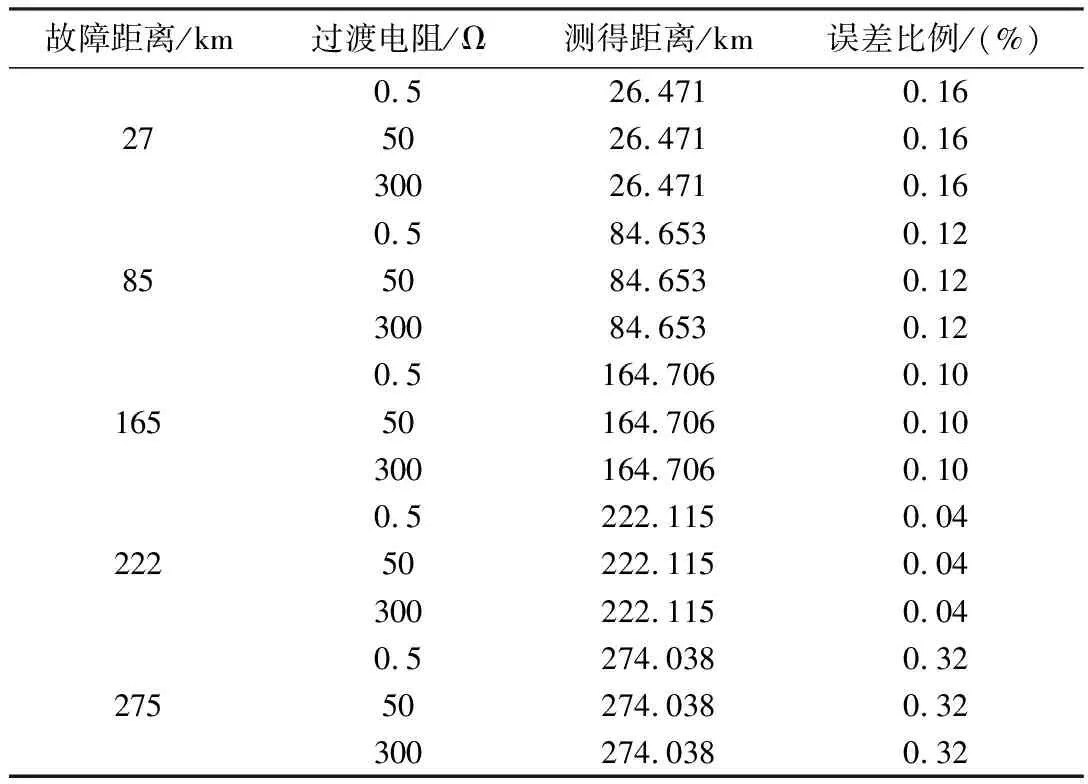
表2 故障测距结果

由表2可知，用平稳小波变换进行故障测距，测距结果不受过渡电阻和故障距离的影响，且有较高的测距精度。

3 结束语

针对行波波速和行波波头识别问题，提出一种不受波速影响，并能在分析故障行波信号时更方便、更准确的基于平稳小波变换的行波法故障测距方法。通过大量的仿真结果表明，该方法具有较高的测距精度，满足电力系统中故障定位的要求。