改进果蝇优化算法的工程项目信息数据处理

张建浩， 任核权， 章剑光， 谢天祥， 胡丹

(1.国家电网绍兴电力局电力经济技术研究所，浙江 绍兴 312000；2.绍兴大明电力设计院有限公司，浙江 绍兴 312000)

0 引 言

随着人工智能的逐步应用，采用人工智能方式管理工程项目信息将得到进一步发展[1]。但是以人工智能方式对工程项目信息进行管理会存在搜索信息效率低、优化差等问题，因此还需研究出更好的解决方法[2-3]。

为解决此类问题，学者们提出了一些随机启发式算法。文献[4]方法提出了一种混合和谐搜索算法(hybrid harmonious search algorithm，HHSA)来研究工程信息管理优化问题的顺序二次规划，该方法虽然通过搜索的方式实现了最佳信息的寻求，但是对于工程问题存在的技术缺点(即对初始值的敏感性，更复杂的导数和所需的更多枚举存储)很难处理。文献[5]方法提出了一种改进的量子人工鱼算法(improved quantum artificial fish algorithm，IQAFSA)，该算法不需要目标函数和约束的微分，能够快速进行计算，但是实际工程项目信息管理问题是高度复杂的，该方法无法在处理大数据过程中保证算法函数的优化质量。

1 工程项目信息管理系统设计

针对上述技术存在的问题，本文提出了一种基于线性递减步长和逻辑混沌映射(diminishing step and logistic chaos mapping, DSLC)的果蝇优化算法(fruit fly optimization algorithm, FOA)以解决工程项目信息管理问题，其创新点在于：

图1 工程项目信息 管理系统结构框图

(1) 将FOA的固定步骤更改为线性递减步骤，对于提高果蝇优化算法的准确性非常有效，以避免陷入局部优化。

(2) 采用DSLC-FOA可以削弱优化解决方案初始条件的敏感性，减少初始化参数对工程项目信息管理最优解的影响，并提高FOA的稳定性。

管理系统架构如图1所示。

如图1所示，工程项目包括所有材料数据与机器的采购、检测、入库、领用、台账、检查、维护和试验到报废全过程的信息化数据[6]。通过主机、虚拟器、存储器和网络等软件，构建“有线+无线”数据采集平台，做到对工程项目数据的全覆盖。通过适当的传输方式实时传输并存储到云数据库中。经过数据处理平台上DSLC-FOA集成处理工程项目信息管理数据，应用服务模块收到数据访问，多用户方式实现数据访问与数据存储的通信，通过一致性服务能够维护账户服务与通信存储服务的进程[7-8]。

2 DSLC-FOA模型

本文提出了一种DSLC-FOA来优化工程项目信息管理设计，整个算法模型的改进包括以下三个部分：

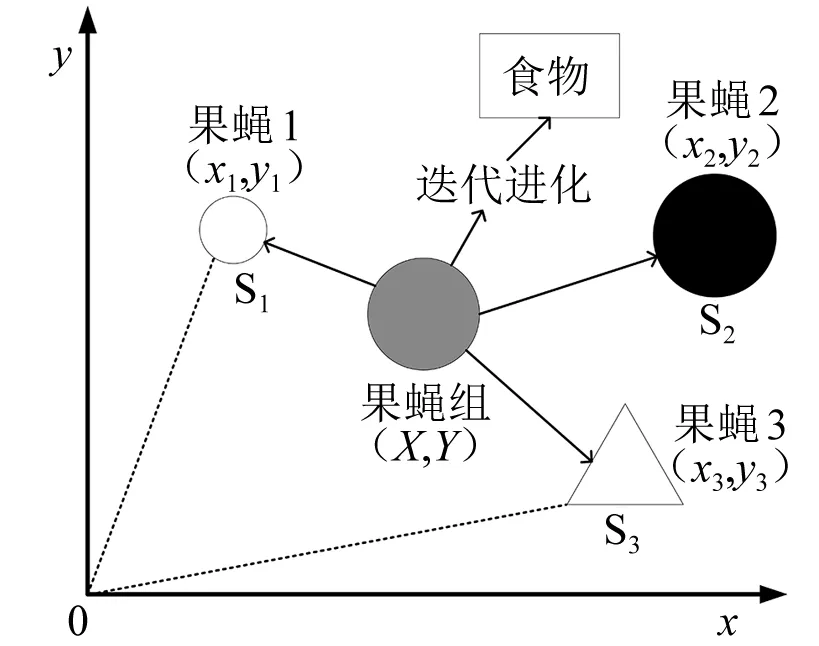
图2 果蝇优化算法的迭代过程

(1) 迭代过程将传统固定步骤更改为线性递减步骤。

(2) 引入逻辑混沌映射理论。

(3) 基于云计算技术数据集成处理。

果蝇搜索有用信息的迭代过程如图2所示。

2.1 线性递减步骤

在FOA的处理中，当迭代步骤固定时，很难找到工程管理项目数据信息的位置。工程管理项目数据信息在最后几次迭代处理时，一些个体的果蝇离工程管理项目数据信息可能越来越远。

考虑到FOA的缺点，第一个改进步骤是将固定步骤更改为线性递减步骤，以避免陷入局部优化并提高准确性。具体改进如下：

(1)

式中：S为初始迭代步长；S′为实际步长；Gmax为最大迭代次数；α为数据参数，其固定值为0.8。

2.2 引入逻辑混沌映射理论

为了减少初始化工程项目信息参数对解的影响并增强FOA的稳定性，第二个改进步骤是利用逻辑混沌映射理论。表达式如下：

x(n+1)=ux(n)[1-x(n)],x(n)∈[0,1]

(2)

式中：n为工程项目信息检索的迭代次数；u为混沌控制工程项目信息参数。上述工程项目信息搜索系统表现出混沌行为。工程项目信息混沌变量的计算公式如下：

Cx(n+1)i=4Cx(n)i[1-Cx(n)i]

(3)

式中：Cx(n)i为工程项目信息检索n次迭代后的第i个混沌变量。当Cxi∈[0，1]和Cx(n)i∈{0.25，0.50，0.75}时，系统处于混沌状态。xi∈[ai，bi]可用Cxi通过式(4)和式(5)进行如下更改：

Cxi=(xi-ai)/(bi-ai)

(4)

(5)

式中：Cxi为工程项目信息混沌变量；xi为第i个工程项目信息混沌变量的值，该变量在进行混沌映射变换后转换为常规变量；bi、ai为xi的取值上下限。

2.3 基于云计算技术数据集成处理

在对工程项目信息管理系统的最优路径分析中，本文利用云计算技术在工程项目数据库中对工程项目信息管理数据进行信息化数据整合，实现数据的集中管理，使工程项目信息管理数据能够动态地获取。获取工程项目信息数据的具体步骤如下。

在整合数据管理过程中，设整体工程项目信息管理数据集为X(项目集X包括整个建筑工程所有建材与机器的采购、检测、入库、领用、台账、检查、维护和试验到报废全过程的信息化数据)，在项目集X中挑选k个数据对首个频繁项集Y1(工程项目维护与试验数据集合)进行构造，其数据的选取原则为：P≥Q。其中：P为数据的求取概率；Q为项目集的最小支持度。Y1构造表达式具体为：

Y1=X(k-y)

(6)

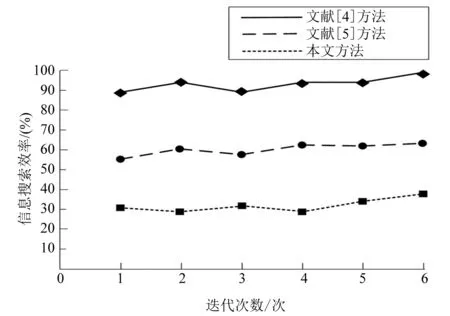
式中：y为频繁项集Y1中的构造数据项。构造数据的候选集C(工程项目维护数据集合)与其第二个频繁项集Y2(工程项目建材入库数据集合)，其中候选集C中的构造数据项需要在首个项集Y1中选出，选择基准为刨除包含非频繁项目的二维项目集E(工程建材采购数据集合)；第二个频繁项集Y2则在候选集C中选取数据，其数据的选取原则为：P

C=Y1(k-y)-E

(7)

Y2=C(k-x)

(8)

式中：x为频繁项集Y2中的构成项。当首个频繁项集Y1和第二个频繁项集Y2的构成项，满足x=y时，对二者进行合并，同理合并其他频繁项集，最终完成候选集的构造。

(9)

式中：Yn为第n个频繁项集；Yn+1为第n+1个频繁项集；yi为第n个频繁项集Yn中的构成项；xi为第n+1个频繁项集Yn+1中的构成项。

然后同上一步骤，构造数据的第n个频繁项集；在构造的n个频繁项集中对关联规则进行考察，其关联规则置信度公式为：

Confidence(Yn>Yn+1)=P(Yn|Yn+1)

(10)

式中：Confidence为置信度，获取n个频繁项集中预设值小于置信度的关联规则，对符合该规则的数据动态获取。

3 试验与分析

为了验证DSLC-FOA算法的实用性和有效性，对于DSLC-FOA算法的优化质量与数据搜索效率设计试验。

3.1 试验环境与数据集构建

本文采用的计算机操作系统为Windows10，64位，计算机的开发工具为[21]Visual Studio 2017，OpenCV 3.0。计算机的硬件环境为CPU：Inter(R)Core(TM)i7；主频为2.59 GHz；内存16 G，仿真模型采用MATLAB软件。

关于试验数据集的构建，本文应用了甘肃省兰州市X建筑公司某工程项目的信息数据库，从该信息数据库中取10 000条工程项目信息数据作为试验数据，其中，取代号5216—5220段铁塔工程项目进行碰撞检查，发现之前工程项目CAD设计图中的7处设计错误数据如表1所示，工程项目目标成本数据如表2所示。

表1 工程项目碰撞问题

表2 工程项目目标成本数据表 元

3.2 优化质量测试

为了突显DSLC-FOA的优化质量优势，与文献[4]方法提出的HHSA和文献[5]方法所采用的改进的IQAFSA进行了比较。试验针对DSLC-FOA在维度(D)为10的基准函数上进行了测试，关于基准函数采用格里旺克函数，用于测试优化后的工程项目设计处理效率，关于格里旺克函数在数学领域上的定义式为：

(11)

在对比试验中，三种算法都选择了相同的通用参数，最大迭代均为300次。所有算法使用MATLAB软件在不同的随机种子下运行50次，所得到的结果是统计试验数据的最优解、最差解、平均最小值和标准差，其统计结果如表3所示。

表3 三种算法的统计结果

从表3的结果可以明显看出，DSLC-FOA在得到的计算结果优于其他两种算法，并且标准偏差表明DSLC-FOA更加稳定而不是文献[4]方法所提出的HHSA和文献[5]方法所采用的IQAFSA。这是因为DSLC-FOA将固定步骤更改为线性递减步骤，以避免陷入局部优化并提高了准确性。

三种优化算法的格里旺克函数最佳函数值的平均值如图3所示。

通过观察图3可得，三种不同的曲线分别显示了HHSA、IQAFSA和DSLC-FOA格里旺克函数最佳函数值的平均值的变化趋势，可以明显看出DSLC-FOA的收敛速度和优化效率明显优于其他两种算法。

图3 三种算法的格里旺克函数收敛曲线

3.3 数据搜索效率测试

为了验证DSLC-FOA的数据处理效率的优势性，分别采用文献[4]方法所提出的HHSA、文献[5]方法所采用的IQAFSA和DSLC-FOA对工程项目信息管理数据进行6次搜索后，比较不同方法的工程项目信息管理数据的搜索效率。关于不同方法的工程项目信息管理数据的搜索效率对比结果如图4所示。

图4 不同方法数据搜索效率对比

分析图4可知，采用不同方法对工程项目信息管理数据进行6次搜索后，HHSA的平均数据搜索效率为61%，IQAFSA的平均数据搜索效率为32%，而本文所提方法的平均数据搜索效率为95%。由此可知，本文所提方法的工程项目信息管理数据的搜索效率较高。

4 结束语

本文提出了将线性递减步骤与逻辑混沌映射理论相结合的DSLC-FOA实现工程项目设计优化。其中，线性递减步骤对于提高FOA的准确性非常有效，同时，逻辑混沌映射可以削弱优化解决方案初始条件的敏感性，并提高FOA的稳定性。采用云计算技术，可动态获取工程项目信息管理数据。试验结果表明，本文研究所用算法更加适用可靠。