基于最值攀爬算法的直挂式储能关键技术研究

王昊, 张文超, 严辉强, 丁超, 裘鹏

(1.杭州模储科技有限公司,浙江 杭州 310000；2.浙江大学 电气学院,浙江 杭州 310000； 3.国网浙江省电力有限公司电力科学研究院,浙江 杭州 310000)

0 引 言

电池储能系统(battery energy storage system，BESS)可以提供多种关键辅助服务，需要对BESS中组件进行充分建模，以适当地反映电池储能系统的行为和性能[1-3]。文献[4]公开了基于电压源变换器平衡基频模型和直流环节动力学，基于一组线性微分代数方程，提出了电压角稳定分析的BESS广义数学模型。但是，过程控制系统(process control system，PCS)模块对系统性能的影响没有建模，并且在不同的微电网条件下，如负载重和/或不平衡的情况下，对模型的性能没有进行研究。文献[5]主要研究BESS在电力系统中主站和子站的监测系统，这种方法能够对各系统设备进行详细监测，但数据传输速度缓慢，会影响网源协调系统的工作效率。

1 关键技术

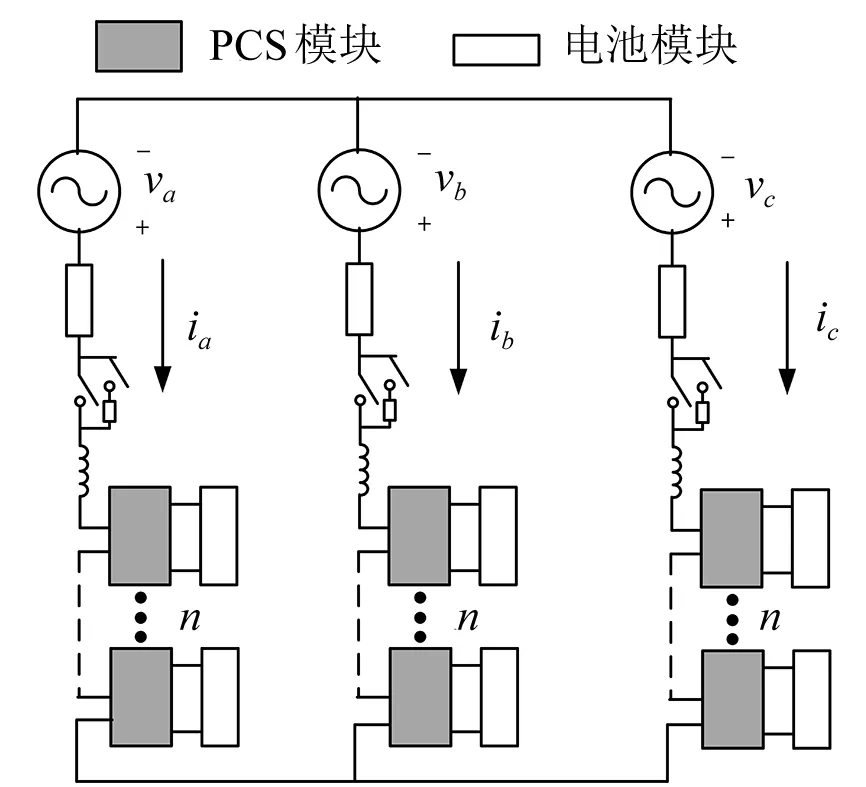
图1 直挂式储能系统电路图

针对上述技术存在的问题，本文搭建电池储能管理系统，其中关键技术包含了直挂式电池储能个人通信服务(personal communications service, PCS)的优化设计，解决了储能电池电压大幅波动工况下的效率优化问题。基于新型最值攀爬(max-min hill-climbing, MMHC)算法提高电池储能管理系统的性能。

1.1 直挂式电池储能PCS的优化设计

直挂式电池储能系统主电路结构如图1所示。

图1中：PCS模块为三相星形联结，经过滤波电感、交流熔断器和预充电装置接入中高压电网。每一相由n个功率模块级联而成，而每个功率模块主要由功率器件及其驱动电路、母线电容、直流熔断器和电池侧预充电装置组成。在PCS模块的交流侧有一个双向开关或接触器，用以在模块故障时将其切除，PCS模块直流侧则通过高压电缆与电池模块进行连接[6-7]。针对图1中直挂式电池储能PCS的优化设计过程如下。

步骤1：优化条件参数。在直挂式电池储能系统中，PCS的输出电压由n个功率模块的输出叠加得到，则有：

(1)

式中:k为三相电源a、b、c；dkj为三相电源k相中第j个功率模块的开关函数；ekj为三相电源k相中第j个PCS模块的直流母线电压，此处即电池模块电压。

由基尔霍夫电压定律可以得到PCS的网侧电压关系为：

(2)

式中:vsk为三相电源k相电压；vo为指整个直挂式电池储能系统的零序电压分量；Ls为整个直挂式电池储能系统的电感值。由PCS的输出电压以及三相电源电压确定。对于k相第j个PCS模块，其对应电池模块的充放电电流ikj即为：

(3)

于是可以得到对应电池模块的荷电状态(state of charge，SOC)模型即：

(4)

式中:SOCkj(0)为第j个电池模块SOC的初始值；Qn为第j个电池模块的额定容量。

结合式(1)～式(4)可以得出，直挂式电池储能系统的电池模块芯片级系统(system on chip，SOC)值与电池模块电压e有关。除此之外，需要满足电池储能系统整体的额定功率[8]，则电池单体总数量n必须为：

(5)

式中:ceil为向上取整函数；E为电池单体额定电压;F为充放电倍率；P为PCS模块额定有功功率；Q为PCS模块额定无功功率。

除以上条件外，电池单体总电压也必须满足一定条件以保证整个系统的正常运行，其条件公式为[9]：

(6)

式中:NE为电池单体总电压；εc为电池单体电压波动系数；V为三相电源额定相电压幅值；f0为PCS模块多电平变换器的功率器件开关频率;Ls为PCS模块输出电感值；I为网侧额定电流幅值。

步骤2：可靠性评估。为了分析出直挂式电池储能PCS的优化效果，本文主要针对功率器件的可靠性进行评估。在PCS模块中，本文采用的绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)在可控性以及电池功率转换效率等方面具有优越的性能，通常计算IGBT的可靠度R一般由式(7)得出[10]。

R(t)=e-λt

(7)

式中:λ为IGBT的故障率。简化分析时可当λ为一常数，可取100 FIT(1 FIT=1/109h)。在大容量直挂式电池储能系统中，PCS模块故障时将会被及时旁路退出，此时如果考虑故障模块的可维修性，则平均无故障时间(mean time between failure, MTBF)即为：

(8)

通过等式(7)～式(8)计算得出直挂式电池储能系统所有模块的平均无故障时间MTBF，通过该参数对整个直挂式电池储能PCS进行合理评估。

图2 PCS优化设计流程图

步骤3：PCS优化流程程序。前文对直挂式大容量电池储能PCS方案在电池条件参数需求与可靠性进行了分析，下面给出PCS优化设计的流程程序，如图2所示。

1.2 新型MMHC算法

为了提高电池储能管理系统的数据处理效率，本文采用基于最值算法(max-min hill algorithm，MAG)的新型MMHC算法，如式(9)所示。

BIC(Σg)=-2ln(lg(Σ|g)+ln(N)(2|V|+|E|))

(9)

式中:lg(Σ|g)为MMHC算法拓扑g渐近函数;|V|和|E|分别为MMHC算法拓扑g中网络节点数目和网络边界E的数目；Σ为与g相关的正态线性模型的协方差矩阵的最大渐近估计值。

关于MMHC算法拓扑g中的节点数目V是通过一组线性方程V=B•V+c得出，其中,B={βij}为一个β矩阵，使得(1-B)是可逆的；c为一个随机误差矢量。极大似然估计Σ可以通过使用残差迭代条件拟合算法来得出，相应的计算公式为：

Σ=(1-B)Ω(1-B)-T

(10)

式中:Ω为协方差矩阵。根据广义的分数分解性质，lg(Σ|g)可按MMHC算法拓扑g的C分量分解。MMHC算法拓扑g的C分量对应于其双向部分的连通分量，即去除所有有向边后由MMHC算法拓扑g生成的MAG图，其表达式为：

(11)

等式(11)中的每个sk对应一个C分量，可以通过等式(12)计算出。

(12)

式中:Ck为C分量k中的节点；Pag(Ck)为Ck中节点的父节点；gk为MMHC算法拓扑g对Ck∪Pag(Ck)交集中的边缘化节点；σ为指与父节点k对应的Σgk的对角线条数目。

通过以上定义公式，将MMHC算法应用于电池储能系统当中。MMHC算法程序如图3所示。

算法1:MMHC算法程序input: Data set D over V with N samples, tolerance tol, significance threshold α, maximum conditioning set max Koutput:g, score BIC//first phase: identifying admissible pairs;P← mmpcSkeleton(D,α,max K);//second phase: greedy score search;S ← corr(D);g ← empty graph;C ← {V∈V};foreachCk∈C dosk ← scoreContrib(Ck, 1, N);endcur Score ←-2Σsk+ ln(N)(2V + E);minScore← cur Score;repeatforeach pair (X, Y ) ∈Pdoforeach action in {addLeft, addRight,orientLeft, orientRight, remove, re-verse} doif action is applicable and does not create directed or almost directed cyclesthen(s’,C’,g’)← updateScores(X, Y,action, s, C,g,tol, N) cur Score ←-2Σsk+ ln(N)(2V + E);if cur Score < minScorethen(sB, CB,gB) ←(s’,C’,g’);end(s, C,g) ←(sB, CB,gB);minScore ←-2ΣskB+ ln(N)(2V + E);until no action reduces minScore;BIC←minScore图3 MMHC算法程序

2 试验与分析

图4 大容量电池 储能电站示意图

为了验证本文搭建电池储能管理系统中采用的两项关键技术的可靠性和实用性，2020年在X市某个清洁电池储能站进行“10 MW级电池储能电站关键技术研究及试点工作”，该示范工程已运行若干月，至今运行良好，整个系统的示意图如图4所示。

关于其电池相关数据参数如表1所示。

试验一：对于优化PCS的可靠性评估，本文通过对比不同的PCS拓扑形式以及IGBT的数量n，通过式(8)分别计算MTBF值。关于试验对比所采用的不同PCS模块拓扑及其IGBT数量如表2所示。

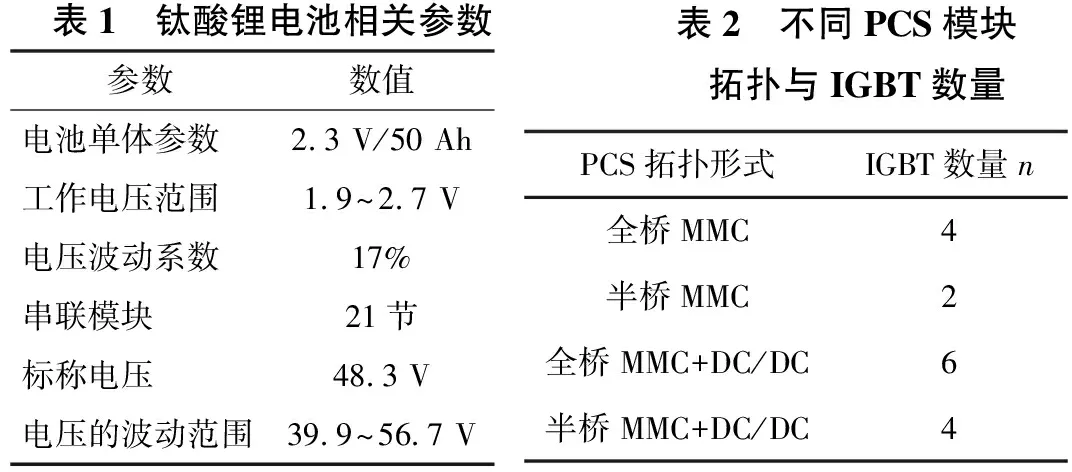
表1 钛酸锂电池相关参数参数数值电池单体参数2.3 V/50 Ah工作电压范围1.9～2.7 V电压波动系数17%串联模块21节标称电压48.3 V电压的波动范围39.9～56.7 V表2 不同PCS模块拓扑与IGBT数量PCS拓扑形式IGBT数量n全桥MMC4半桥MMC2全桥MMC+DC/DC6半桥MMC+DC/DC4

在仅考虑功率器件的情况下，储能PCS的可靠性与其冗余子模块Nr数直接相关。而本文试验案例中自变量采用了冗余比η，其主要定义的是整个高压直挂式电池储能系统中，冗余子模块数与子模块数的比值，无论哪种PCS拓扑形式，在保持冗余比相同的情况下，模块数越多，其可靠性越低，但降低得并不大。关于不同PCS拓扑形式的MTBF比较如图5所示。

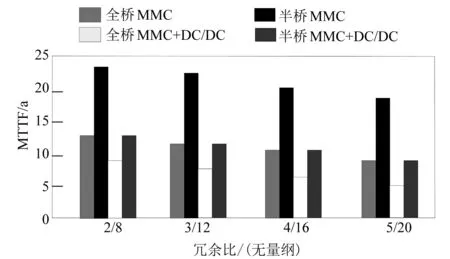
图5 不同PCS拓扑的平均无故障时间

从图5可以看出，横轴选取2/8、3/12、4/16、5/20四种冗余比η，在相同模块数以及冗余比的情况下，各种PCS拓扑间的 MTBF 差异较大，其中半桥MMC的MTBF最高，全桥MMC+DC/DC 的MTBF最低，这表明采用半桥MMC的PCS 拓扑可靠性最高。因此，半桥MMC拓扑及2个IGBT模块为直挂式电池储能PCS的最优设计。

试验二：为了验证本文采用基于MAG的新型MMHC算法处理电池储能相关数据的实时性，与MMHC算法进行对比试验。试验所用的电池储能数据均由高压直挂式电池储能系统中传感器采集。输入的电池储能数据样本信息如表3所示。

表3 变电站参数数据信息表

从试验数据集中提取0～2 GB电池储能基础数据量，根据数据大小和延迟时间为轴绘制曲线图，如图6所示。

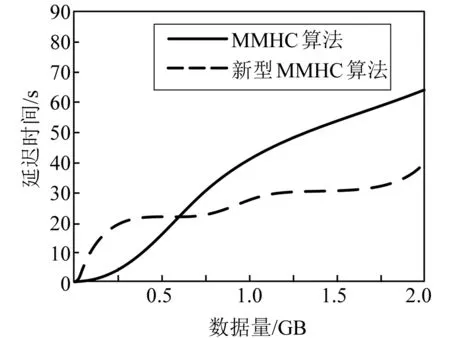
图6 两种算法所需时间对比

从图6可知，本文所开发的新型MMHC算法处理电池储能数据耗时更短、效率更高。这是因为MAG使得MMHC算法能够快速搜索电池储能相关数据，能够表现出MMHC算法的适用性。

3 结束语

本文以高压直挂大容量电池储能管理系统为对象，提出了一种新型混合MMHC算法和直挂式电池储能PCS的优化设计方法。通过计算最佳N、NE、n、Ls和f0等优化条件参数，计算不同模块数量、电感值及开关频率等配置下的可靠度，采用MMHC算法处理电池储能数据性能最好。然而，在PCS 拓扑选择以及MMHC算法的参数设置等方面尚存在诸多问题，需要进一步研究。