物料参数对立式搅拌釜混合性能影响的模拟

（江西理工大学江西省颗粒系统仿真与模拟重点实验室， 江西赣州341000）

颗粒混合是工业生产过程中最重要的单元操作之一，广泛应用于化工、 结晶、 冶金、 食品、 医药、 建材等领域中。颗粒混合是指2种或2种以上不同性质的颗粒，在力的作用下进入彼此区域内的过程[1]。颗粒混合时同时存在扩散混合、对流混合与剪切混合3种混合过程，通常初期以对流混合为主，中期以扩散混合为主，剪切混合则贯穿整个过程。在搅拌釜中，颗粒围绕搅拌轴进行混合，体现的主要方式为剪切混合与扩散混合。剪切混合是指在颗粒区域内颗粒受到剪切作用发生相对运动的过程；扩散混合是由于颗粒的紊乱运动而导致相邻颗粒相互交换位置所产生的局部混合，混合物料的差异会带来显著不同的混合效果。

离散颗粒在不同条件下分别具备固体、 液体、 气体的部分性质，内部运动机理非常复杂[2]。为了探究颗粒搅拌混合机理，部分学者采用了实验研究的方法，采用正电子发射粒子跟踪技术（PEPT）将颗粒的运动三维可视化，应用于双螺杆造粒机[3-4]、 犁耙混合机[5]、 流化床[6]、 转桶[2]以及搅拌釜等的研究中，粒子图像测速技术（PIV）在搅拌釜的研究中也广泛应用。例如，Cole等[7]采用PEPT技术深入探究泡沫浮选等应用的内部运输过程和颗粒、 流体、 气泡的相互作用机理，研究三相搅拌罐式反应器中固体-流体的搅拌混合过程。韩定强等[8]基于仿生学思想设计了一种鲸尾型搅拌桨，运用2D-PIV设备进行流场研究，发现新型桨叶可以提高最大径向速度和搅拌罐下部的轴向速度，搅拌桨产生的流场混沌程度更高，混合性能更好。Conway等[9]利用PIV技术测量了单分散、 多分散颗粒材料的瞬时速度、平均速度和波动速度，发现在多分散颗粒材料中，通过改变剪切速率能观察到不同的分离机制。Stewart等[10]应用PEPT技术研究搅拌釜低转速下（10 r/min）玻璃珠摩擦系数对混合性能的影响，并且观察到颗粒流的运动形态是漩涡状，但实验方法始终受到耗时长、设备贵等因素的限制，需要更好的方法来降低研究成本。

随着数值模拟技术趋于成熟， 越来越多的学者使用数值模拟技术进行颗粒混合的研究[11-16]。 相对于传统实验， 数值模拟所需的时间更短， 成本更低， 不受外界环境的干扰。 近年来， 离散单元法（DEM）成为颗粒动力学研究的重要方法之一， 可以计算和分析颗粒间的碰撞， 获取颗粒群运动的信息[17]。 Siraj[18]利用DEM研究了单片桨叶搅拌釜中2种不同粒径单分散颗粒的混合性能， 分析3种不同桨叶形状和桨叶角度对混合性能的影响。Saeed等[19]使用DEM研究了在搅拌釜中颗粒形状对混合性能的影响。 Havlica等[20]采用实验与数值模拟相结合的方法对二元玻璃珠的混合过程进行研究，发现粒子在低速时更容易从底部及桨叶后方朝转轴处靠近。 此外， 一些学者也针对无挡板搅拌釜内部的固液混合进行了研究[21-22]。 目前，关于搅拌过程的研究主要考虑搅拌釜结构参数改变带来的影响， 而在工程应用中， 即便同一类型待搅拌物料的参数也不尽相同， 所以研究不同物料参数对搅拌过程的影响至关重要， 是扩大搅拌釜适用范围和节能增效的必要前提。 为此， 结合颗粒的空间合角速度（离散元软件中对颗粒角速度的定义）和混合度， 对不同物料参数下无挡板搅拌槽内颗粒混合性能的变化进行系统研究， 选取颗粒粒径、 密度以及颗粒间的摩擦系数3种参数。 先讨论颗粒粒径的影响， 选出最佳粒径组合之后进一步分析颗粒密度和颗粒间摩擦系数对混合性能的影响。 使用软件为吉林大学于建群教授团队自主研发的拥有完全知识产权的离散元软件AgriCAE， 该软件的适用性已经在多项研究中得到了广泛验证[23-25]。

1 离散元法模型

离散元法通过建立固体颗粒系统的参数化模型，来模拟颗粒的行为并分析颗粒的运动，所有粒子的平动和转动运动都是通过求解牛顿运动方程来完成[13]，方程表达式为

（1）

（2）

式中:mi为颗粒i的质量， kg；vi为颗粒i的平移速度， m/s；fc, ij为颗粒i和颗粒j之间的接触力， N；fd, ij为颗粒i和颗粒j之间的黏性阻尼力， N；Ii是颗粒i的转动惯量， kg·m2；ωi是颗粒i的角速度， rad/s；Mt, ij和Mr, ij分别代表颗粒i和颗粒j之间的切向摩擦力矩和滚动摩擦力矩， N·m。

2 模型参数及分析方法

2.1 模型参数

参考Boonkanokwong[26]的实验数据， 选择采用的搅拌釜为圆柱形四叶搅拌釜， 示意图见图1。 颗粒密度为2 525 kg/m3， 不同粒径的颗粒总体积相等。 进料方式采用双入料口同时进料， 颗粒生成时无初速度， 自由下落。

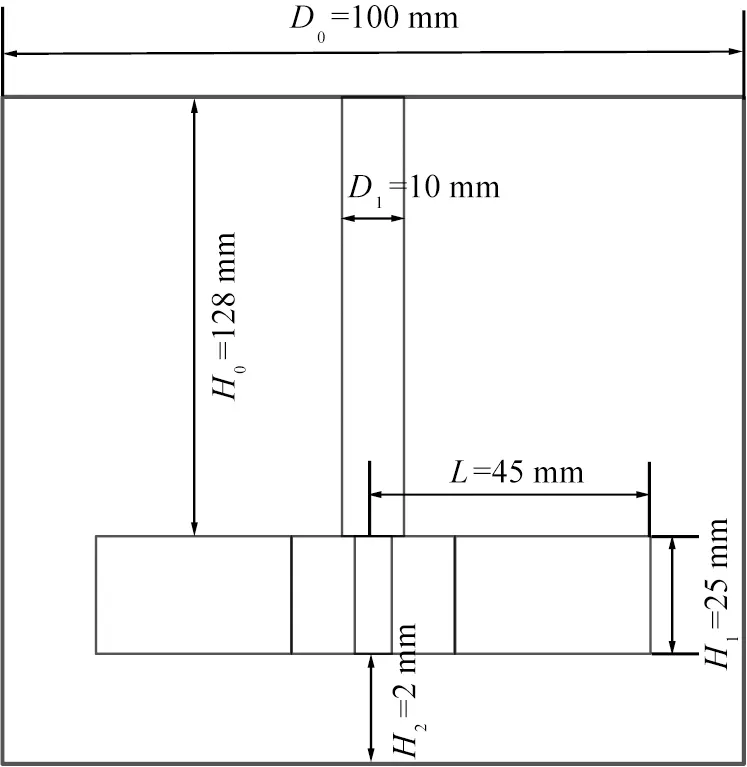
图1 搅拌釜示意图Fig.1 Sketch of stirred tank

2.2 分析方法

结合颗粒空间合角速度与混合度分析搅拌釜的混合性能，颗粒的空间合角速度可以从计算结果中提取，混合度则需要其他方法进行评价，常用的评价方法有接触数评价法[27]、 Lacey指数评价法[28]、 临近混合指数评价法、 标准差评价法和变异系数评价法[29]等。每种评价法适用的范围不同：Lacey指数评价法、 临近混合指数评价法适用于径向混合运动；变异系数评价法适用于轴向混合；变异系数评价法和接触数评价法多用于数值模拟中。Van Puyvelde等[30]提出接触数来评价混合度的方法，通过大小颗粒接触数与颗粒总的接触数的比值来评价混合度，表达式为

（3）

式中：q为混合度；Csl为不同颗粒之间的接触数；Ct为所有颗粒的接触数。

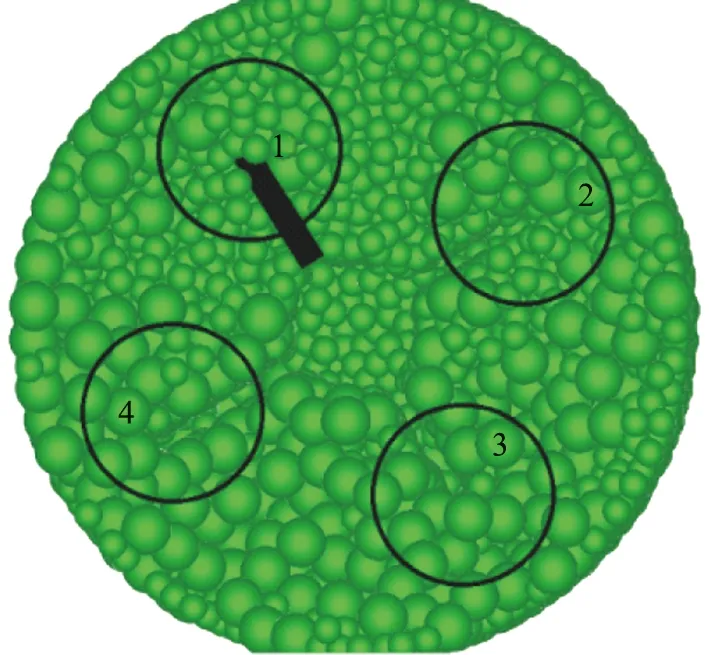
图2 表面取样示意图Fig.2 Surface sampling diagram

研究采用表层颗粒混合度来分析各参数对混合度的影响：选取不同时间点，在模拟结果的表面圈分4个直径为26.32 mm的圆，圆心与搅拌轴中心距为13 mm。为了保证较高的准确性，取4个圆平面的混合度平均值，圆平面取样示意图如图2所示。

3 结果及讨论

3.1 颗粒粒径对混合性能的影响

为了研究粒径对颗粒混合性能的影响， 颗粒的密度和颗粒间摩擦系数保持不变， 选取基础颗粒粒径为3.5 mm， 混合对象分别为粒径2.5、 3.0、 4.0、 5.0 mm的颗粒。 软件可以对所有颗粒进行编号， 为了方便对比， 结合颗粒的初始空间位置， 选取了编号分别为100、 500、 1 000、 3 000的颗粒， 针对其空间合角速度进行分析对比。图3为3.5、 5.0 mm组合下取样颗粒的初始空间位置示意图。

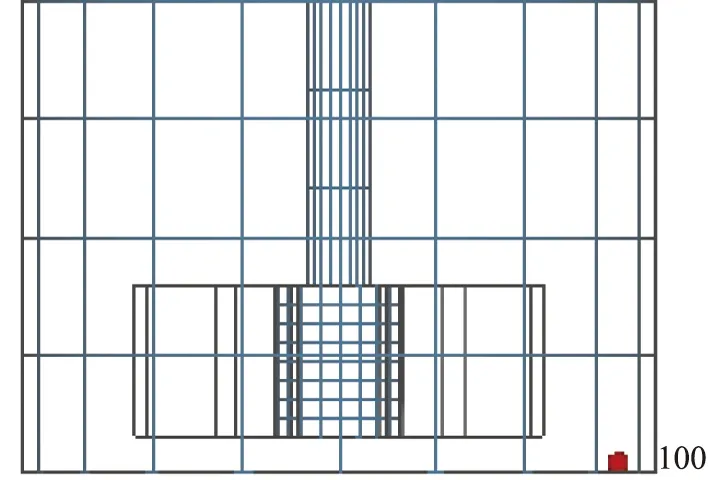
（a）编号100

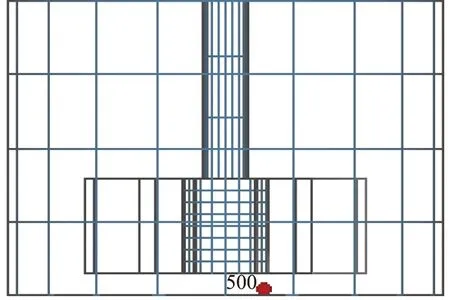
（b）编号500

（c）编号1000

（d）编号3000

不同粒径组合下取样颗粒的空间合角速度见图4，由图可以看出，3.5、 2.5 mm组合的空间合角速度整体上比其他颗粒组合的更大。此外，随着颗粒粒径的不断变大，颗粒空间合角速度振幅越来越小，说明颗粒粒径越大，角速度越小。

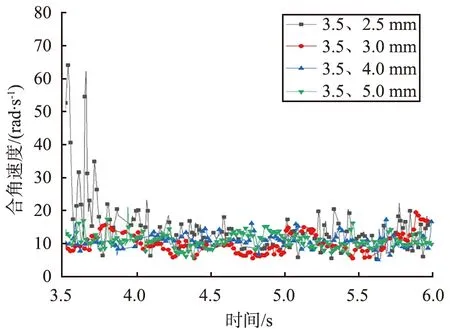
（a）编号100

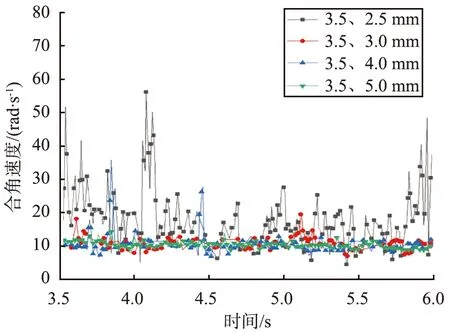
（b）编号500

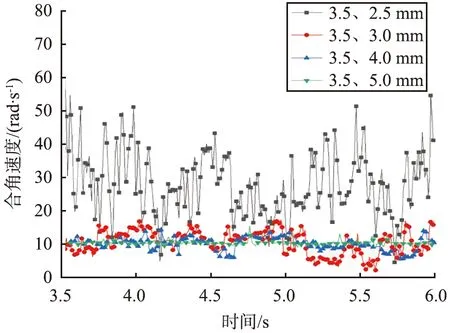
（c）编号100

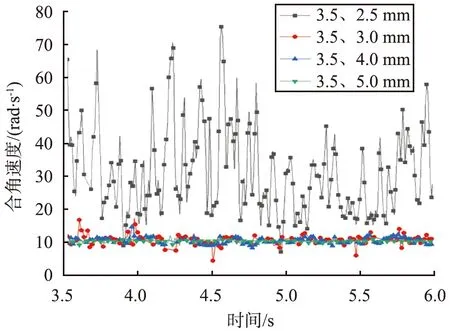
（d）编号3000

为了进一步分析粒径对混合性能的影响， 统计3.6、 4.2、 4.8、 5.4、 6.0 s的混合度。 颗粒粒径对表面混合度的影响如图5所示。 从整体来看， 最终表面混合度均在0.25～0.45之间， 3.5、 2.5 mm组合的表面混合度最大， 但混合时间较长， 这是因为颗粒粒径小， 数量多； 3.5、 3.0 mm组合与3.5、 2.5 mm组合的混合度接近； 3.5、 5.0 mm组合的混合效果最差。 总的来说， 随着粒径的减小， 颗粒的混合度在不断增大。

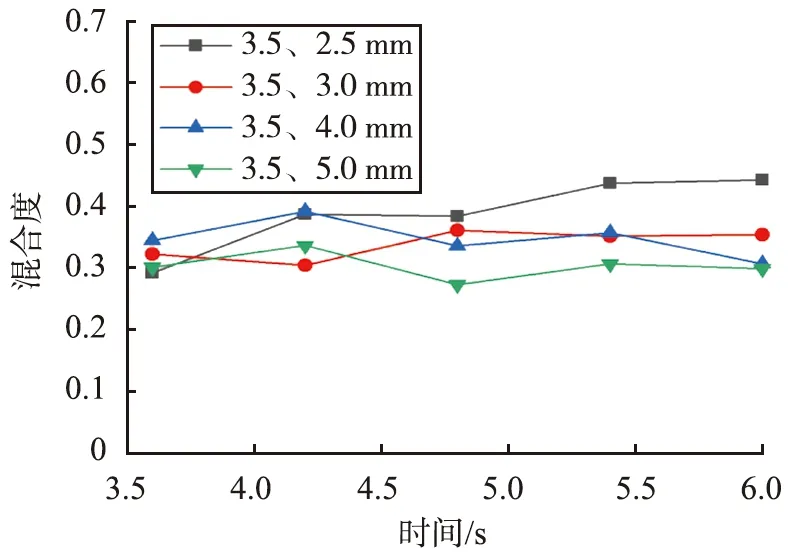
图5 不同粒径组合下颗粒的混合度Fig.5 Mixing degree of particles at different diameter combinations

3.2 颗粒密度对混合性能的影响

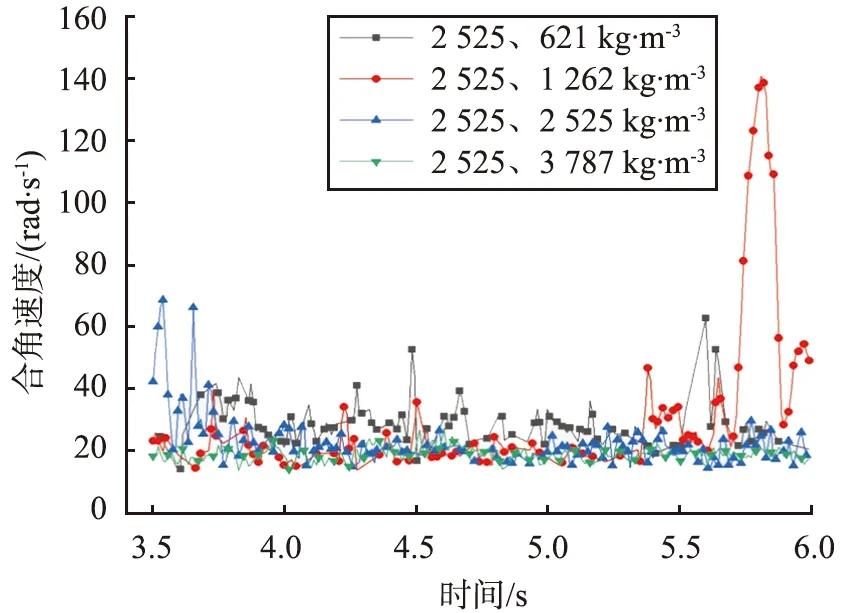
（a）编号100

（b）编号500

（c）编号100

（d）编号300

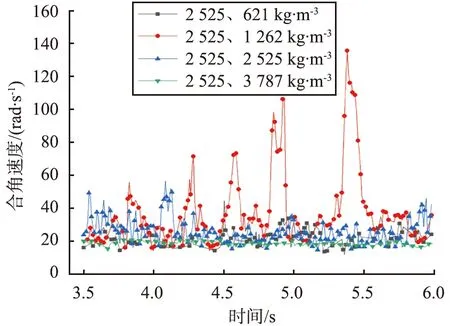
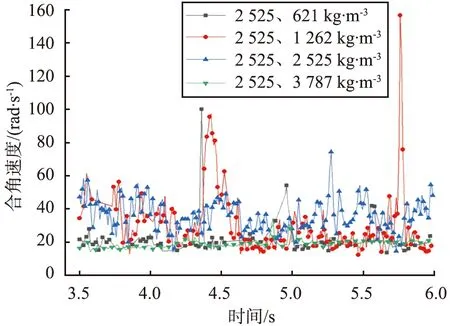
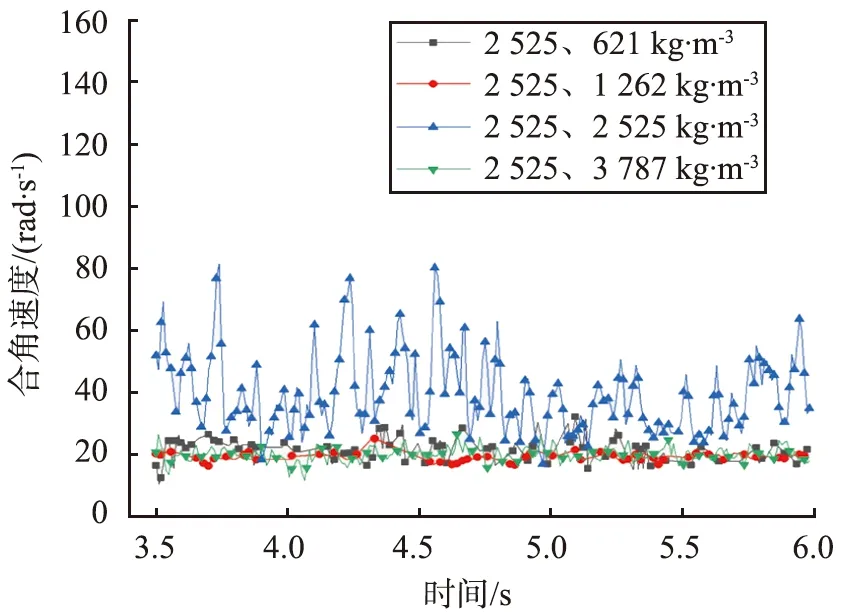
图6为不同颗粒密度组合下取样颗粒的空间合角速度分析图。由图可见，密度为2 525、 2 525 kg/m3组合的合角速度普遍比其他组合的大， 且模拟结果显示该组合的混合度最大， 进一步表明合角速度越大，混合效果越好。

编号100的颗粒为大颗粒，其他颗粒为小颗粒，大颗粒的合角速度较小。同时，模拟结果显示，颗粒密度差大，会导致颗粒间的分层，如密度为2 525、 621 kg/m3的组合，搅拌过程中密度小的颗粒向上运动，密度大的颗粒向下沉降，导致混合效果不佳。

4种不同颗粒密度组合下的表面混合度如图7所示。从图中可看出，颗粒密度为2 525、 621 kg/m3组合时，表面颗粒的混合度效果最差，q在0.1～0.2之间。而密度为2 525、 2 525 kg/m3组合时，混合度最大。表明颗粒密度差越小，混合度越大。

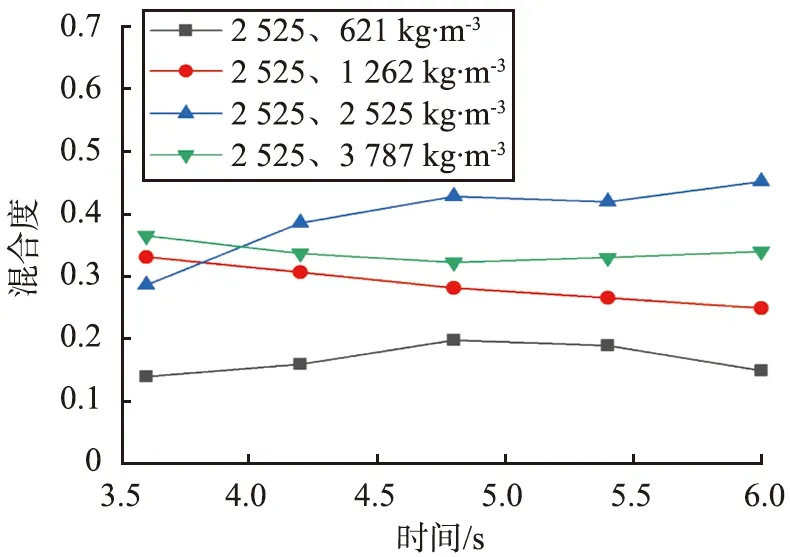
图7 不同密度组合颗粒的混合度Fig.7 Mixing degree of particles at different density combinations

3.3 颗粒间的摩擦系数对混合性能的影响

（a）编号100

（b）编号500

（c）编号1000

（d）编号3000

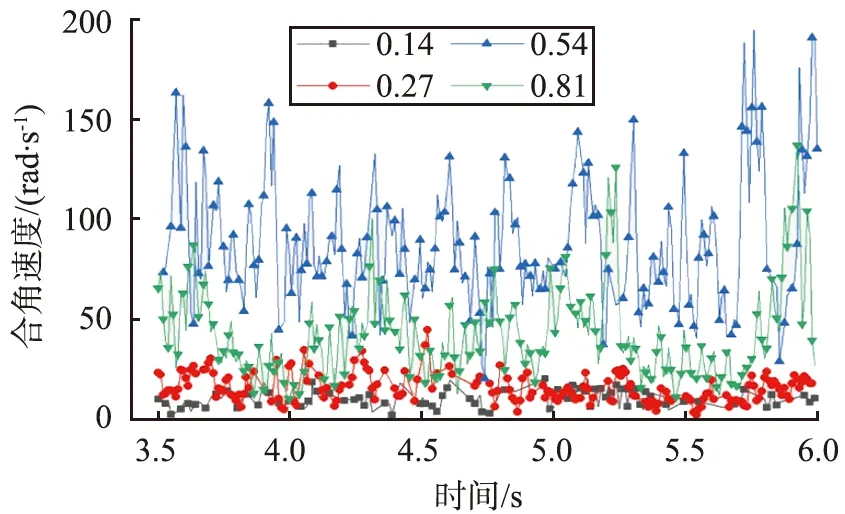
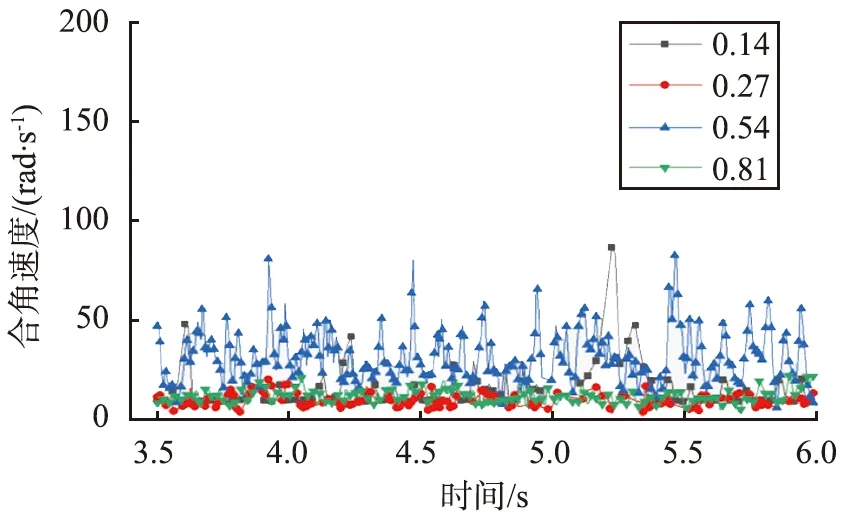
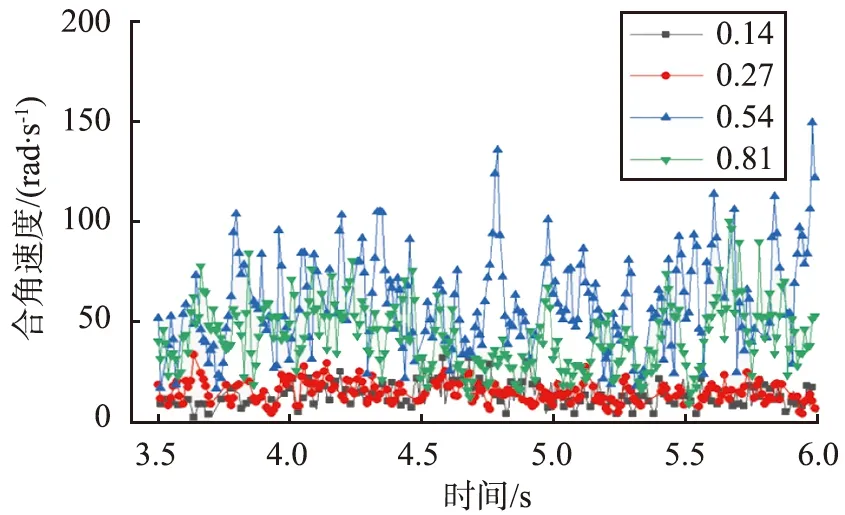
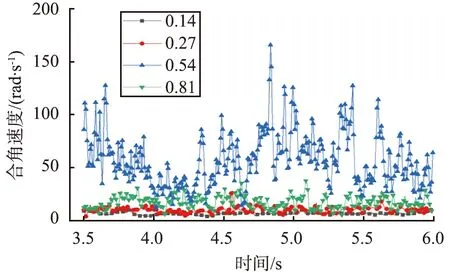
为了探究摩擦系数对颗粒混合性能的影响，采用2种颗粒密度均为2 525 kg/m3，直径分别为3.5、 2.5 mm，4组摩擦系数分别是0.14、 0.27、 0.54和0.81。图8为不同摩擦系数下取样颗粒的空间合角速度。由图可以看出，当摩擦系数为0.54时，颗粒的合角速度最大，其次是摩擦系数为0.81和0.27；摩擦系数为0.14时颗粒的合角速度最小。

摩擦系数的增加会导致颗粒表面变得粗糙， 彼此间的运动范围变大， 颗粒的混合程度得到提高， 但系数太大则会导致颗粒无法克服阻力运动， 颗粒混合效果反而变差。 图9为不同摩擦系数下颗粒的混合度。 从图中可以看出， 颗粒间的摩擦系数对混合度有着显著的影响， 当摩擦系数为0.14时，q值在0.1以下， 混合度非常小。 当摩擦系数变大时， 混合度也随之增加。 表面混合度最大的是摩擦系数为0.54的颗粒组合，q值在0.4～0.5之间， 且随时间的变化不大， 在3.6 s时达到了稳定状态。 总体上，颗粒混合度随着摩擦系数的增大先增加后减小， 在0.54时达到最大。

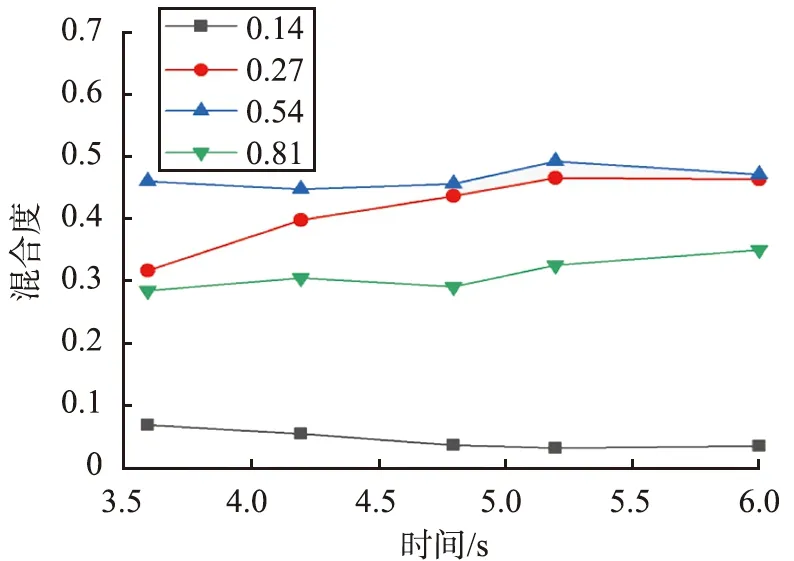
图9 不同摩擦系数下颗粒的混合度Fig.9 Mixing degree of particles at different friction coefficients

4 结论

针对不同物料参数对颗粒混合状态的影响进行了研究，结合颗粒的空间合角速度以及混合度对模拟结果进行分析。结果显示，颗粒空间合角速度的大小与混合度的大小并非相对应。在颗粒密度变化时，密度为2 525、 621 kg/m3组合的合角速度最大，但是密度为2 525、 2 525 kg/m3组合的混合效果最好。在摩擦系数变化时，空间合角速度与混合度变化一致，摩擦系数为0.54时，混合效果最好，此时，颗粒的空间合角速度最大且相对稳定。

混合度的分析结果更直接体现了不同参数改变对混合效果的影响。 不同粒径组合的颗粒混合度相差不大， 整体的混合度均在0.25～0.45之间； 相较于颗粒粒径， 颗粒密度的影响较大， 颗粒组合的密度差越大， 混合度越小， 颗粒密度组合为2 525、 2 525kg/m3时的混合度最大； 颗粒间的摩擦系数变化时， 颗粒混合度随着摩擦系数的增大先增加后减小， 在摩擦系数为0.54时混合度最大。 纵向对比颗粒粒径、 颗粒密度、 颗粒间摩擦系数对混合性能的影响， 颗粒间摩擦系数对混合度影响较大， 混合度在0.1～0.5之间波动。