稀土Ce3+/Eu2+离子和点缺陷发光性质的第一性原理研究

闻 军，黄晓晓，宁利新，段昌奎

（1.安庆师范大学 电子工程与智能制造学院，安徽 安庆 246133；2.安徽师范大学光电材料科学与技术安徽省重点实验室，安徽 芜湖 241000；3.中国科学技术大学 物理系，安徽 合肥 230026）

1 引 言

稀土发光材料在当代科学研究和能源信息领域中均都发挥着非常重要的作用[1-2]，例如它们在照明、显示、探测器、激光器、太阳电池、生物荧光标记、量子信息等方面具有广泛应用。特别是，Ce3+和Eu2+离子掺杂的无机荧光粉具有宽激发带、高效可见光发射、热稳定性好、显色指数高等特点，因而在白光发光二极管（Light-emitting diode，LED）中具有重要应用[3-8]。众所周知，物质的结构是决定其性质的根本因素之一。为了研究Ce3+和Eu2+离子掺杂的荧光粉中化学组分变化影响其微观结构、进而调控发光性质的关键机理问题，人们利用各种实验结构表征以及光谱测量分析手段对材料的结构以及性质进行了大量、卓有成效的研究[9-11]。需要指出的是，有时人们难以直接获得杂质掺杂或缺陷引入导致的原子位移以及结构畸变等关键信息。基于结构表征以及光谱测量等实验研究有时难以直接分析发光中心与配位环境以及其中缺陷之间的物理作用过程。理论计算手段可以为解决上述问题提供一种可行、可信的研究方案，从而为实验研究提供有力补充。

稀土发光材料的理论计算研究手段主要有密度泛函理论计算、多组态相互作用从头计算以及唯象模型分析。一直以来，人们主要利用唯象模型分析手段对稀土发光材料的发光性质进行理论研究，例如，晶体场理论[12-13]、Judd-Ofelt理论[14-16]以及Dorenbos经验模型[17-23]。近些年来，研究者们发展的第一性原理计算方法能够准确处理稀土离子4f和5d电子，从而为开展稀土发光材料的理论研究提供了新思路、新方案。通过密度泛函理论几何构型优化计算，可以获得在稀土离子各种复杂掺杂情形下体系稳定原子结构，据此可以计算获得基质中稀土离子与点缺陷的局域结构信息、热力学稳定性、电子结构、光跃迁能量及强度等[24-35]。因此，可以分析稀土发光材料的自激活发光、热释发光、长余辉发光、光致发光等发光物理过程以及杂质或点缺陷在上述发光过程中的可能作用。

本文主要介绍作者与合作者近年来利用理论计算模拟手段在稀土发光材料研究领域开展的主要研究工作以及获得的结果。第二部分主要介绍第一性原理计算方法，包括密度泛函理论计算、点缺陷计算以及多组态相互作用从头计算。第三、四部分分别介绍作者与合作者在固体中点缺陷的热力学稳定性与发光机理阐释、荧光粉中Ce3+和Eu2+离子4f→5d跃迁模拟与激发光谱指认方面开展的第一性原理研究工作。最后对本文进行了归纳、总结，并对稀土发光材料的第一性原理计算研究领域的机遇和挑战进行了简要总结。

2 第一性原理计算方法

2.1 密度泛函理论计算

密度泛函理论计算是一套标准的、用于处理稀土发光材料中缺陷或杂质的几何结构、热力学性质、电子结构以及发光性质的第一性原理计算方法[36]。在密度泛函理论框架下，研究者们可将电子密度分布作为基本变量用于研究体系的基态性质。Kohn和Sham通过引入非相互作用参考系统，精确处理并获得总能中动能的主要部分[37]。总能中其余较小部分主要包括电子-电子相互作用的非经典部分、自相互作用修正以及非相互作用参考系统未包含的动能的一部分。该部分可以通过各种近似形式的交换关联泛函（例如局域密度近似、广义梯度近似以及杂化密度泛函等）来处理[38-39]。密度泛函理论计算已被证明在描述诸如原子结构、电荷密度、形成能等多方面具有较高精度。研究者们通过构建超单胞模型来模拟完美的以及含有缺陷或杂质的各种情形的晶体结构，如图1所示。图中给出的是具有多种阳离子格位的Ca3（PO4）2晶体结构；其中掺杂离子（例如Ce3+和Eu2+离子）可能占据5种Ca格位。当掺杂离子与被替代离子价态不一致时，我们通常引入点缺陷以保证体系电中性。电荷补偿的点缺陷一般位于掺杂离子近邻配位环境中，这是由于掺杂离子与点缺陷具有相反电荷态。利用VASP[40-41]等主流的材料模拟计算软件对模型进行密度泛函理论计算，优化确定体系的稳定构型并计算获得总能量，进一步还可以计算获得体系稳定性（例如，热力学稳定性、动力学稳定性等）、电子结构（例如，能带结构、能态密度、电荷密度等）、缺陷性质以及光学性质（例如，介电常数、光吸收系数等）。

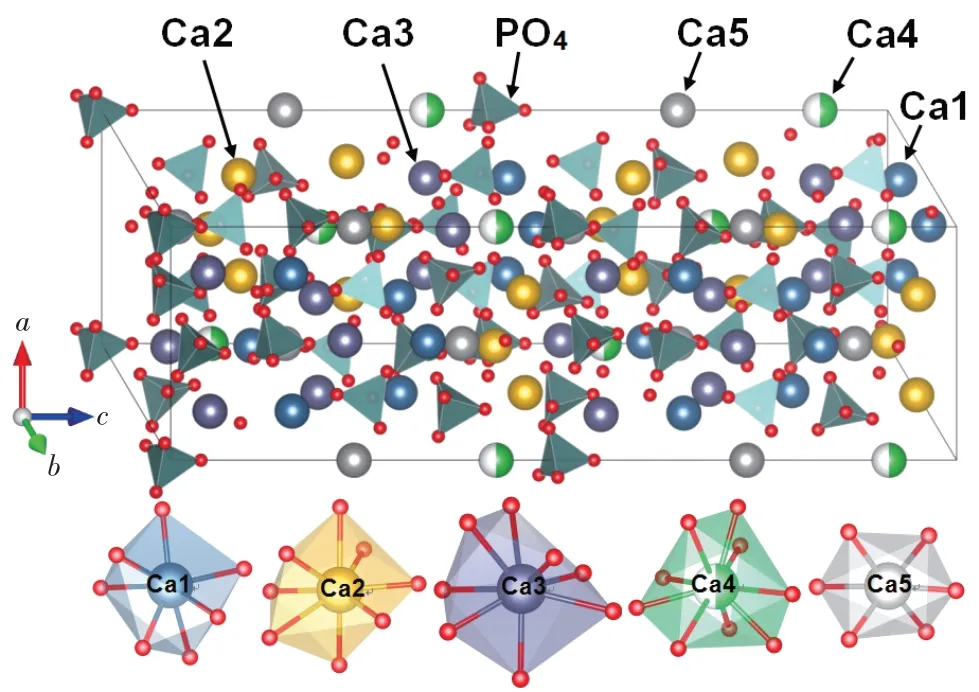
图1 Ca3（PO4）2晶体结构以及其中不同Ca格位的局域结构Fig.1 Schematic representations of the crystal structure and local structures of the Ca sites of the Ca3（PO4）2 crystal

为了准确预测固体基质带隙以及带隙中缺陷或杂质态位置，采用合理的密度泛函理论计算方法非常关键。通常的密度泛函理论计算（基于局域密度近似和广义梯度近似）由于采用局域交换能量近似而存在电子自相互作用问题，导致轨道过度离域化，从而严重低估基质带隙并且难以描述稀土离子的局域化4f电子。另一方面，Hartree-Fock理论只包含精确交换而无关联项，这会导致轨道的过度局域化。因此，我们通常选择杂化密度泛函理论计算方法（例如,PBE0和HSE杂化泛函）[42-44]。它们通过包含一部分Hartree-Fock精确交换能来实现对于基质带隙以及缺陷或缺陷态位置的准确描述。此外，通常采用投影缀加平面波（Projected-augmented wave，PAW）方法来描述原子离子实与价电子之间的相互作用。

2.2 点缺陷的第一性原理计算

在稀土发光材料的制备过程中，本征点缺陷通常会不可避免地产生。它们既可以作为稀土离子杂质异价掺杂时的电荷补偿中心，也可以作为导带电子或价带空穴的陷阱中心。在热力学平衡下，材料中缺陷或杂质的浓度是关于形成能的函数。具有电荷态q的缺陷或杂质（D）的形成能定义为[45-46]：

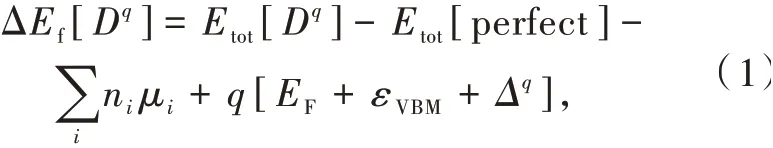
其中，Etot[Dq]和Etot[perfect]分别表示含有缺陷或杂质Dq的晶体和完美晶体的超单胞总能量，它们可以通过对相应超单胞进行密度泛函理论计算获得。考虑到兼顾杂化密度泛函理论几何构型优化效率以及消除杂质（或缺陷）镜像电荷影响，我们通常选取的超单胞（含有杂质或缺陷）边长约为1.0 nm。μi表示体系中第i种元素的原子化学势。ni表示从完美晶体超单胞中添加或者移除第i种元素原子的数量。当原子被移除时，ni取值为负；当原子被添加时，ni取值为正。EF是体系的费米能级，εVBM是体系的价带顶。Δq是超单胞有限尺寸以及周期性边界条件导致的电荷态依赖的修正项[47]。考虑到我们通常关注接近电中性的情况以及所选取超单胞大小（边长约1.0 nm），弛豫后的能量修正较小（例如对|q|=1情形，约0.1～0.2eV），因此我们的计算通常忽略Δq。

原子化学势通常依赖于实验合成制备条件。一般利用体相单质中单原子能量来近似代替晶体中相应原子化学势，例如，SrLiAl3N4（SLA）中金属元素Sr、Li以及Al原子。对于诸如氧、氮等原子，一般通过热平衡关系来确定其原子化学势，即晶体化学式单元的总能量（通过完美晶体的单胞总能量确定）等于化学式单元中所有原子的化学势之和。例如，SLA中N原子化学势可通过关系式μSr+μLi+3μAl+4μN=μbulk来确定（其中，μbulk代表SLA一个化学式对应的总能量）。从公式（1）可以看出，缺陷或杂质的形成能随着费米能级（在基质带隙中）变化曲线斜率的绝对值对应缺陷或杂质所带电荷数，斜率的正负号对应着含有缺陷的超单胞的正负性。计算的缺陷或杂质的形成能越高，表明在基质中缺陷或杂质存在的可能性越小。

基质中缺陷或杂质会在基质带隙或靠近能带边引入能级。这些能级与缺陷或杂质不同电荷态之间的转变过程相关。这意味着，从能带结构计算获得的缺陷或杂质Kohn-Sham能级不能直接被指认为是与上述实验或物理过程相关的能级。基质中缺陷或杂质的热力学转变能级ε（q2/q1）可以定义为具有电荷态q1和q2的缺陷或杂质形成能相等时体系费米能级在基质带隙中的位置，如下式（参见图2（a））[46]：

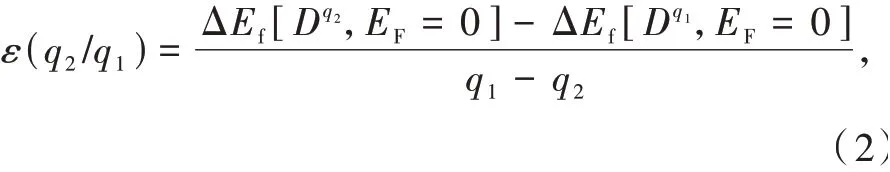
其中，ΔEf[Dq1,EF=0]和ΔEf[Dq2,EF=0]分别为密度泛函理论计算的缺陷或杂质Dq1和Dq2在费米能级位于价带顶时的形成能。在公式（2）中计算形成能时，所选取的包含缺陷或杂质Dq1和Dq2的超单胞应处于相应平衡构型，如图2（b）所示。热力学转变能级可以利用深能级瞬态谱实验观测确定；然而对于浅中心情形，上述能级则与热电离能对应[48]。缺陷或杂质的光跃迁能级εopt（q2/q1）与热力学转变能级定义（公式（2））类似。需要指出的是，在光跃迁能级计算公式中跃迁末态的几何构型与初态保持一致，如图2（b）所示。跃迁后，缺陷或杂质的末电荷态无法弛豫至平衡构型时，光跃迁能级即可通过实验观测确定。从公式（2）可看出，缺陷或杂质的热力学转变能级与光跃迁能级不依赖于原子化学势的取值。

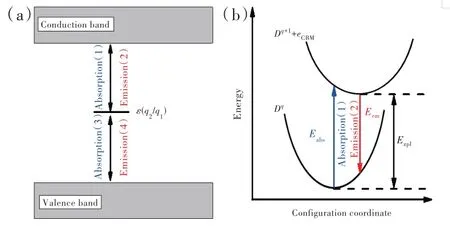
图2 （a）缺陷或杂质能级与基质导带以及价带之间电子交换相关的吸收、发射过程；（b）光跃迁过程（1）和（2）对应的位型坐标图。Fig.2（a）Schematic representations for the absorption and emission processes associated with the electron exchange between the defect level of the D and the conduction band or valence band.（b）Configuration-coordinate descriptions for the optical transition processes（1）and（2）.

2.3 多组态相互作用从头计算

利用密度泛函理论计算确定的稳定几何构型进行基于波函数理论的镶嵌团簇从头计算，可以获得荧光粉中掺杂Ce3+和Eu2+离子的4f→5d跃迁能量以及振子强度。首先，根据优化的稳定原子结构，构造以Ce3+或Eu2+离子为中心的镶嵌离子团簇，如图3所示。利用从头计算模型势（Ab-initiomodel potential，AIMP）[49]中 的相对论核势来模拟中心团簇环境[50]，中心团簇通常由掺杂离子和最近邻配位离子构成，有时也会包含次近邻配位离子（尺寸再大的中心团簇通常不再考虑）。中心团簇的构成主要取决于所研究具体问题需要，例如在Ce3+离子掺杂Y3Al5O12体系中，中心团簇除了包含Ce3+离子及其最近邻8个O2-离子外，还包含2个次近邻Al3+离子[51]。进而，我们可以准确处理Si—N共取代（Si4+替换Al3+以及N3-替换O2-）对于其中掺杂Ce3+离子4f和5d能级的影响。需要说明的是，将次近邻配位离子（须与中心离子距离较近）纳入至中心团簇对于稀土离子最低5d能级结果有一定改善，但同时也会增加计算量。根据测试计算，我们发现包含最近邻和次近邻配位离子情形（大中心团簇）的多数5d晶体场能级比只包含最近邻配位离子情形（小中心团簇）的相应能级升高。特别是对于Ce3+离子最低5d1能级，大中心团簇比小中心团簇通常升高约1 000～2 000 cm-1。例 如，对 于X2-Y2SiO5∶Ce3+体 系，团 簇（CeY1O6Si4）7+比（CeY1O6）9-计算的Ce3+离子最低的5d1能级升高1 880 cm-1（Y1格位），团簇（CeY2O7Si4）5+比（CeY2O7）11-的5d1能 级 升 高1 993 cm-1（Y2格位）[52]。可以根据只包含最近邻配位离子的计算结果与实验光谱的对比，分析确定是否需要增大中心团簇的尺寸。利用AIMP镶嵌势[53]描述中心团簇以外3～5个配位层内的晶格环境，从而防止配位阴离子被过分极化。如前所述，当掺杂离子与被替代离子价态不一致时，我们同样会在掺杂离子局域环境（中心团簇内或其外围晶格环境）中引入用于电荷补偿的点缺陷。利用点电荷[54]表示AIMP以外的周围离子，确保体系电中性并充分考虑团簇与点电荷环境之间的有效衔接。其次，主要采用MOLCAS程序中组态相互作用、二级微扰修正以及自旋-轨道耦合作用模块对镶嵌团簇进行从头计算[55-63]。对于掺杂Ce3+和Eu2+离子，采用相对论有效核势（[Kr]核）以及（14s10p10d8f3g）/[6s5p6d4f1g]高斯价电子基组；对于O2-离子，采用[He]核有效核势以及（5s6p1d）/[2s4p1d]高斯价电子基组。

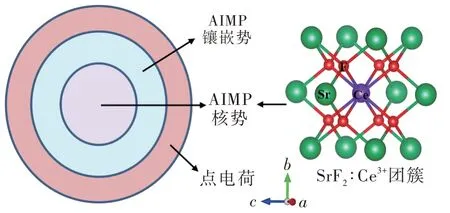
图3 镶嵌团簇模型示意图（以SrF2∶Ce3+为例）Fig.3 Schematic diagrams of the embedded cluster model（taking SrF2∶Ce3+as an example）

程序先对镶嵌体系进行分子轨道计算，通过分析轨道组成找出重要轨道。然后，基于组态相互作用获取精确波函数，并对重要轨道展开的组态空间进行完全活性空间自洽场（Complete-active-space self-consistent field，CASSCF）计 算[55-57]，其中考虑了掺杂离子与配体之间的成键作用和非动态相关作用。对于Ce3+离子来说，完全活性空间是由1个电子分别占据以4f、5d、6s为主要成分的13个分子轨道组成。对于Eu2+离子来说，完全活性空间是由7个电子分别占据以4f、5d、5f为主要成分的19个分子轨道组成。利用多组态二级微扰理论（Complete-active-space second-order perturbation theory，CASPT2）程序[58-61]对能量进行进一步修正，以考虑掺杂离子4f与5d电子之间以及它们与配体电子之间的动态关联作用。最后，根据CASSCF计算的波函数和CASPT2计算的能量结果，利用限制性活性空间态相互作用程序RASSI（Restricted-active-space state-interaction）进行自旋-轨道耦合（Spin-orbit，SO）计算[62-63]，获得Ce3+和Eu2+离子4f和5d能级能量。上述计算考虑了与Ce3+（或Eu2+）离子4f→5d跃迁相关的4f1（或4f7）基态和5d1（或4f65d1）激发组态，在自旋-轨道耦合作用下，最终获得13个（或144个）Kramers双重态。

3 固体中点缺陷的热力学稳定性与发光机理阐释

关于长余辉以及自激活荧光粉的发光机理以及其中电子与空穴陷阱的本质，目前尚未有统一的、令人信服的理论模型。基于杂化密度泛函理论计算，可以获得荧光粉中各种点缺陷的形成能，分析热力学稳定性和电子结构，确定热力学转变能级与光跃迁能级，获得最稳定电荷状态随体系费米能级（其位置对应样品制备时所处的环境气氛）的变化趋势。进一步，将相对容易形成的点缺陷的光跃迁能量与实验热释发光曲线（可确定电子或空穴陷阱的深度）或实验激发光谱直接进行对比，可以确定陷阱或自激活发光的来源，分析荧光粉的热释发光、长余辉发光、自激活发光的物理过程以及点缺陷在上述发光过程中的可能作用[64-72]。

SLA∶Ce3+荧光粉在绿光激发下能够实现黄光到红光的宽带发射。当激发光波长为470 nm时，该荧光粉的发射光谱分别在560 nm和620 nm处各呈现一个发射带。在该荧光粉中，Ce3+离子与被替代Sr2+离子的价态不同，因此体系中存在受主型缺陷以补偿上述价态差异。此外，有文献报道SLA∶Eu2+荧光粉的红色长余辉发光，并提出施主型氮空位是其中可能存在的电子陷阱[73]。我们考虑SLA中20种不同的本征点缺陷，包括两种Li空位（VLi）、两种Sr空位（VSr）、八种N空位（VN）、两种LiSr反位缺陷以及六种LiAl反 位 缺 陷。本 征 点 缺 陷VLi1,2、VSr1,2、LiSr1,2,、LiAl1-6、VN和杂质CeSr在不同电荷态下的形成能随费米能级变化情况如图4（a）～（d）所示[71]。由于SLA通常是在还原气氛下制备，这对应费米能级位于带隙上方且靠近导带的情形。因此，我们可以发现，VLi、VSr、LiSr、LiAl和VN最稳定电荷态分别为-1，-2，-1，-2，+1价。两种CeSr孤立缺陷最稳定电荷态均为+1价，即在占据Sr格位时，Ce3+比Ce4+离子更加稳定。根据密度泛函理论计算的缺陷形成能，我们进一步可以得到各种点缺陷的热力学转变能级，如图5所示。受主型缺陷（VLi、VSr、LiSr和LiAl）可作为价带中空穴的俘获中心；而施主型缺陷（VN）可作为导带中电子的俘获中心。VN+的ε（+/0）能级位于导带底下方0.34～0.74 eV区间内，这说明VN+是合适的电子俘获中心，可以为室温余辉发射提供合适的电子俘获能级。

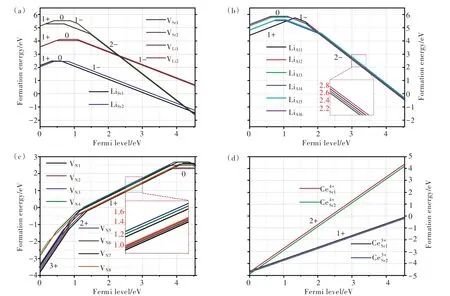
图4 SLA中不同电荷态下本征点缺陷。VLi1，2、VSr1，2、LiSr1，2（a），LiAl1-6（b），VN1-8（c）和孤立缺陷CeSr1，2（d）的形成能与费米能级的关系［71］。Fig.4 Formation energies for intrinsic point defects.VLi1，2，VSr1，2，LiSr1，2（a），LiAl1-6（b），VN1-8（c），and isolated dopants CeSr1，2（d）in different charge states as a function of the Fermi level（EF）position in the band gap of SLA.At each EF position，only the formation energies for the most stable charge states are shown for the point defects［71］.

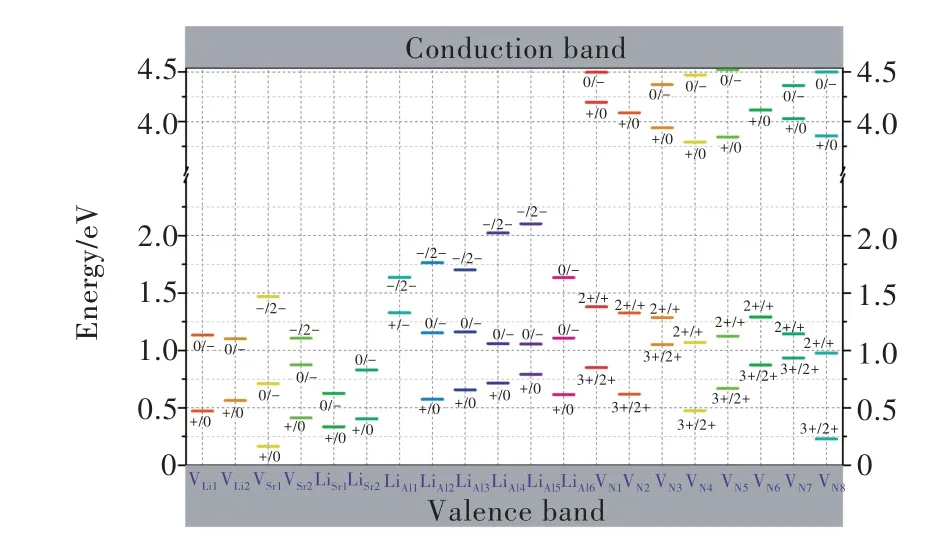
图5 SLA中点缺陷的热力学转变能级在带隙中的分布［71］Fig.5 Summary of calculated thermodynamic transition energy levels for point defects in SLA［71］

未掺杂的磷灰石型M5（PO4）3X（M=Ca，Sr，Ba；X=F，Cl，Br）材料能够实现从蓝光到橙光的精细发光调控[74-77]。缺陷形成能的计算结果表明，三种氧空位（VO）以及三种反位缺陷（XO）的形成能较小，容易在该类基质中产生[72]。我们计算了束缚于上述六种缺陷激子的光跃迁能量，其中具有最低缺陷形成能的氧空位（VO（3））热力学转变能级如图6所示。我们发现，束缚于氧空位的激子光跃迁能量（涉及到εopt（+/0）能级）与实验激发光谱较为吻合。因此，可将M5（PO4）3X体系强烈的自激活发光归结于其中氧空位中性与+1价电荷态之间转变所涉及的光跃迁。此外，根据第一性原理计算，我们发现Li2SrSiO4∶Eu,Dy长余辉荧光粉中中性氧空位可能会捕获导带中电子（来自Eu2+离子4f→5d跃迁）或者接受从价带顶激发而来的电子，变为负一价[69]。热释测量实验中的热激活将使得被捕获的电子脱离处于负一价氧空位（亚稳态），并进入导带成为自由电子。它们很有可能与局域在基质带隙中某些特定缺陷能级上或者位于价带顶的空穴结合，从而产生热释发光。

图6 M5（PO4）3X（M=Sr，Ba；X=Cl，Br）中 具 有 最 小 形成能的氧空 位（VO（3））热力学转变能级ε（1+/0）、ε（2+/0）以及ε（2+/1+）。SPOC、SPOB、BPOC、BPOB分 别 代 表Sr5（PO4）3Cl、Sr5（PO4）3Br、Ba5（PO4）3Cl及Ba5（PO4）3Br，CB和VB分别代表导带和价带［72］。Fig.6 Thermodynamic transition energy levels ε（1+/0），ε（2+/0）and ε（2+/1+）of the VO with the smallest defect formation energy（i.e.，the VO（3））in the M5（PO4）3X（M=Sr，Ba；X=Cl，Br）.SPOC，SPOB，BPOC and BPOB represent Sr5（PO4）3Cl，Sr5（PO4）3Br，Ba5（PO4）3Cl and Ba5（PO4）3Br，respectively.CB and VB represent conduction band and valence band，respectively［72］.

4 荧光粉中Ce3+和Eu2+离子4f→5d跃迁模拟与激发光谱指认

针对荧光粉（例如Ca4F2Si2O7、La2CaB10O19、Ca10M（PO4）（7M=Li，Na，K）、Ba2Y5B5O17、Ba3Y2B6O15、Y3Si5N9O等）中掺杂Ce3+和Eu2+离子的各种可能占据情形[78-89]，优化和计算超单胞几何构型和总能计算，获得实验上通常难以确定的发光中心近邻原子位移和畸变信息，确定稀土离子各种占据情形的出现几率，正确判断稀土离子格位占据偏好以及电荷补偿机制。结合CASSCF/CASPT2/RASSI-SO计算，准确考虑动力学关联效应以及自旋轨道耦合效应，计算的Ce3+和Eu2+离子4f→5d跃迁能量以及相对振子强度能够与实验激发光谱直接进行对比分析，从而能够准确指认荧光粉激发光谱。

许多应用型荧光粉的晶体结构通常较为复杂（例如，多种阳离子格位、无序占据、电荷补偿等情形），单从实验数据或经验晶体场分析难以将光谱与占据格位之间进行关联，例如绿色长余辉材料SrAl2O4∶Eu2+荧光粉。该基质中存在两种Sr格位，分别是格位尺寸相对较大的Sr1格位和相对较小的Sr2格位。虽然人们在绿光发射（室温）和蓝光发射（低温）均来自于Eu2+离子5d→4f跃迁这一问题上已经达成共识，但是具体发光格位归属尚不能确定，更不用说长余辉发光机理。经验晶体场分析结果表明，绿光和蓝光发射分别来自于占据在Sr1和Sr2格位上的Eu2+离子[90-91]。然而，Ce3+离子在SrAl2O4中的格位占据研究[92]间接表明，SrAl2O4∶Eu2+中绿光和蓝光发射可能分别来自于占据在Sr2和Sr1格位上的Eu2+离子。

我们基于密度泛函理论优化的稳定原子结构，构造镶嵌团簇（EuSr1O9）16-和（EuSr2O9）16-，采用基于波函数的多组态相互作用方法（CASSCF/CASPT2/RASSI-SO计算），首次获取了低对称配位环境下EuSr1和EuSr2的4f→5d跃迁能量[86]。通过比较计算结果与实验低温格位选择激发光谱中最低4f→5d跃迁能级的相对位置（图7），可以确定SrAl2O4∶Eu2+中绿光和蓝光发射分别来自于占据尺寸相对较小Sr2和较大Sr1格位的Eu2+离子，解决了长期困扰该荧光粉的重要难题。需要指出的是，从头计算的电子跃迁能量和强度对应着零声子线以及声子边带谱中跃迁强度最大的电-声子跃迁的能量和强度。如需进一步考虑声子振动对光谱展宽的影响，一种较为简单的方法是在每个电子跃迁上叠加一个高斯或者洛伦兹线型展宽[93]。另外，该工作还利用从头计算的中间结果阐明了配位环境影响4f→5d跃迁能量的结构和电子方面的原因，明确指出晶体场劈裂的增加是主导光谱红移的重要因素。

图7 不同监测波长下SrAl2O4∶Eu2+的实验激发光谱（a）、及Sr1（b）和Sr2（c）格位上Eu2+离子4f65d1组态能级计算值［86］。Fig.7 The experimental normalized excitation spectra（a），and schematic diagram for the calculated energies and relative oscillator strengths of the 4f→5d transitions from the 4f7（8S7/2）ground level to the spin-octet levels in the 4f65d1 configuration of EuSr12（+b）and EuSr22+（c）in SrAl2.

原型β-Ca3（PO4）2晶体中有5种金属阳离子格位，其中M1、M2、M3、M5格位为Ca完全占据，M4格位为Ca半数占据（即Ca占据与Ca空位数量比为1∶1），如图1所示。这意味着人们可以通过“晶体工程策略”进行基质组成调变以实现Eu2+离子光色调控。例如，在紫外激发下Eu2+离子发射光谱包含有两个明显分开的谱带[94]：418 nm处的发射峰以及长波长处的宽带，这表明Ca3（PO4）2∶Eu2+中可能存在两种发光中心。当向其中继续加入同价Mg2+离子后，宽带发射强度明显提升[95-96]；当异价M+（Li+、Na+、K+）离子取代M4格位后，Eu2+离子发光颜色可以在紫蓝至黄色范围内进行调谐[97-98]。然而，关于Eu2+离子光谱指认，目前尚无定论，主要原因在于格位配位环境的不规则。我们采用多组态相互作用从头计算方法，对β-Ca3（PO4）2型荧光粉中占据不同格位Eu2+离子4f→5d跃迁能级进行了计算[87]。如图8所示，通过比较最低4f65d1能级的相对位置可以看出，占据M4格位Eu2+离子的最低4f65d1能级位置最高。通过与实验激发光谱比较，进一步指出，窄带发射来自于占据在M4格位上的Eu2+离子，宽带发射则来自于占据在M1～M3格位上的Eu2+离子，对Eu2+激活一系列β-Ca3（PO4）2型荧光粉的发光格位给出了统一解释。

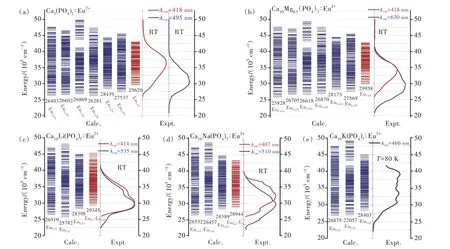
图8 几种Eu2离子激活β-Ca3（PO4）2型发光材料实验激发光谱以及不同格位上Eu2+离子4f65d1能级，其中4f7基态能级设置为0 cm-1［87］。Fig.8 The 4f65d1 energy levels of Eu2+ions at different sites in Eu2+-doped β-Ca3（PO4）2-type phosphors，along with the corresponding experimental excitation spectra.The 4f7 energy level of the ground state of the Eu2+ion is set to be zero［87］.

我们对发光材料中掺杂Ce3+离子的跃迁能量和相对振子强度进行了计算。例如，正硅酸盐Li4SrCa（SiO4）2中有一种Sr和一种Ca格位。两套实验发射光谱和激发光谱表明可能存在两种Ce3+离子发光中心，但这两种发光中心分别来自于占据Sr格位还是Ca格位上的Ce3+离子还不甚清楚。对于该体系，我们构造Ce3+离子占据Sr（或Ca）格位的超单胞模型，并在Ce3+离子的最近邻Ca（或Sr）格位引入Li+离子以保证体系电中性。基于优化获得的体系稳定几何构型，分别计算了两种不同掺杂情形下Ce3+离子4f→5d跃迁能级（图9（a）、（b）），并与实验低温激发光谱比较（图9（c）、（d））；直观指认近紫外发射和蓝光发射分别来自于占据在Sr和Ca格位上的Ce3+离子[88]。分析Ce3+离子5d能级信息，进一步指出晶体场劈裂主导了两种发光中心的相对光谱位移，并结合实验数据获取了两种Ce3+离子最低5d1能级相对于基质导带底的能量，定性讨论了猝灭机制。

图9 从头计算的Li4SrCa（SiO4）2中Ca格位（a）和Sr格 位（b）上Ce3+离子4f1→5di（i=1～5）跃迁示意图以及与实验低温激发光谱（（c）发射波长为455 nm，（d）发射波长为335 nm）的比较［88］。Fig.9 The schematic diagrams for the energies and relative oscillator strengths of the 4f1→5di（i=1-5）transitions for Ce3+ions at Ca（a）and Sr（b）sites in Li4SrCa-（SiO4）2，along with the low temperature excitation spectra（（c）λem=455 nm，（d）λem=335 nm）［88］.

类似地，还计算了蓝色荧光粉Ba2Y5B5O17∶Ce3+和Ba3Y2B6O15∶Ce3+中不同阳离子格位上Ce3+离子4f1和5d1组态能级，如图10（a）、（b）所示[89]。通过比较发现，Ba2Y5B5O17∶Ce3+中最低激发带A1主要源于M2格 位 上Ce3+离 子4f1→5d1跃 迁，窄 带 荧 光 粉Ba3Y2B6O15∶Ce3+的 激 发 带 则 源 于Y2和Y3格 位 上Ce3+离 子4f1→5d1～3跃 迁，这 明 确 排 除 了CeBa的 贡献。因此，我们对两种硼酸盐荧光粉的蓝光来源进行了确切指认。进一步，根据从头计算的5d能级重心以及晶体场分裂值，可以认为Ba3Y2B6O15∶Ce3+中CeY3相对于CeY2的晶体场能级间跃迁（4f1→5d1）能量下降可能是由于前者的平均键长小于后者。同时还可根据计算获取的Ce3+离子最低4f1和5d1能级在基质带隙中的位置（确定其与导带底之间的能量差），估算出Ce3+离子掺杂体系的猝灭温度。我们发现Ba3Y2B6O17∶Ce3+比Ba3Y2B6O15∶Ce3+的猝灭温度高，这与实验测量结果定性一致。

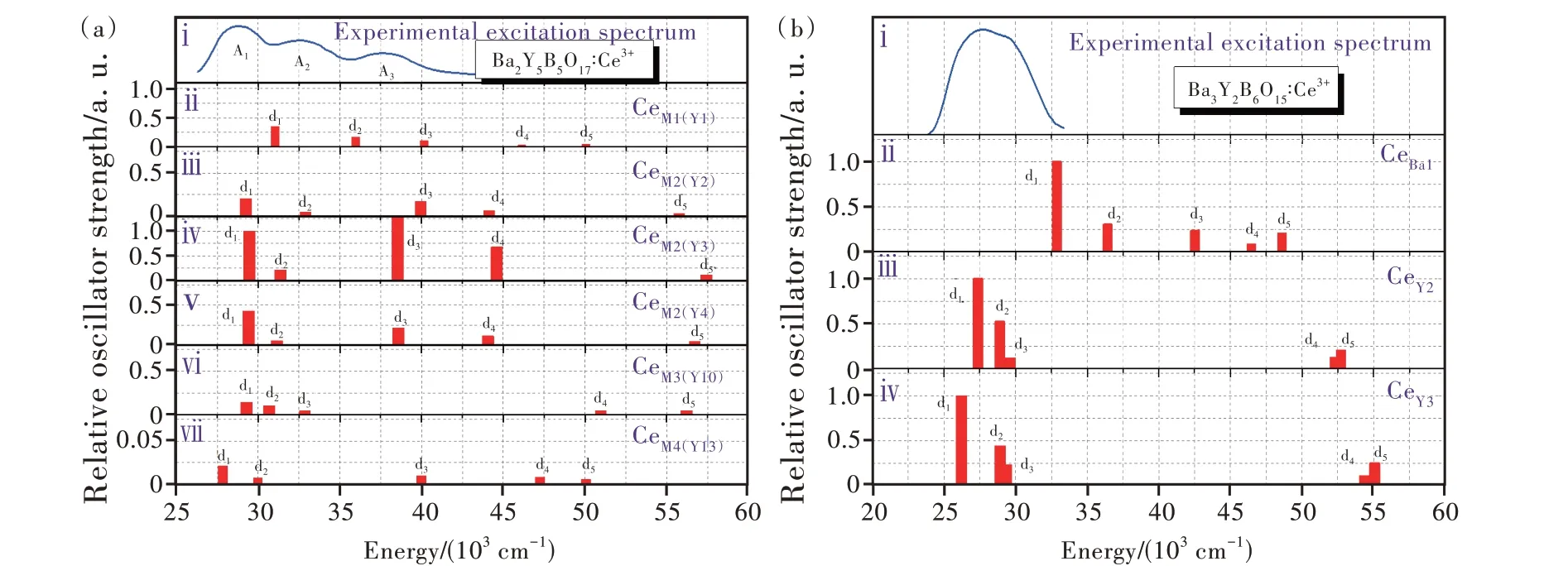
图10 Ba2Y5B5O17（a）和Ba3Y2B6O15（b）中占据不同格位Ce3+离子4f1→5di（i=1～5）跃迁能级以及相应的实验激发光谱［89］。Fig.10 The Schematic diagrams for the energies and relative oscillator strengths of the 4f1→5di（i=1-5）transitions for Ce3+ions at different sites in Ba2Y5B5O17（a）and Ba3Y2B6O15（b），along with the experimental excitation spectra［89］.

5 结论与展望

本文介绍了作者与合作者近年来在固体中点缺陷的热力学稳定性与发光机理阐释、荧光粉中Ce3+和Eu2+离子4f→5d跃迁模拟与激发光谱指认等方面的第一性原理计算研究进展。众所周知，第一性原理计算方法不依赖于实验光谱数据，直接从基质晶体结构和组成出发，通过密度泛函理论（特别是杂化密度泛函理论）计算，获得基质材料中可能存在的本征点缺陷以及实验上难以确定的稀土离子或缺陷的局域原子结构，进而探讨其对于热释发光、长余辉发光、自激活发光、光致发光等各类发光物理过程的可能影响。基于稳定原子结构，通过构建以Ce3+或Eu2+离子为中心的镶嵌离子团簇，结合基于波函数的多组态相互作用从头计算，可以获得掺杂离子4f→5d跃迁能量以及相对振子强度，从而直接指认实验激发光谱并解释相关实验现象。

综上所述，第一性原理计算方法在研究稀土发光材料的原子结构、电子结构和发光性质等方面具有较大优势，对于优化稀土发光材料性能和促进新型材料设计等具有重要推动作用。在该研究领域，目前仍然存在一些机遇和挑战，需要人们持续关注和不断攻关。这些机遇和挑战主要有：

（1）荧光粉的热稳定性是在实际应用中影响发光品质的关键因素，因此研究者们需要对荧光粉的猝灭机制进行研究，以期改善其热稳定性质。目前，人们常用热激发交叉弛豫和电子热电离两种机制解释热猝灭行为。虽然通过计算5d态激发能级距离导带底的能量差可以进行定性分析且具有参考意义，但是由于稀土离子5d电子极易受到局域配位环境影响，上述能量差在不同基质材料中往往表现差异较大。因此，可以将现有计算与材料力学性质计算相结合，探索确定一套有效的计算方法，帮助理解、改善荧光粉的发光热稳定性。

（2）能量传递是实现荧光粉光色调控的重要手段之一。目前，虽然能够被UV有效激发的蓝色和绿色发光材料种类较多，但是高性能的红色荧光粉却极少，主要由于一些常用红色发光中心的能级跃迁禁戒。实验上向其中继续掺入其他稀土离子，通过离子间的能量传递可以实现高效红光发射。我们期望基于理论计算研究手段，从微观角度分析不同发光中心之间的能量传递机理，为红色荧光粉乃至其他荧光材料的能量传递研究提供新思路，为实验制备性能更加优异的白光发光二极管提供理论支持和指导。

（3）Ce3+和Eu2+离子掺杂荧光粉的系列研究成果表明，包括密度泛函理论与多组态相互作用从头计算方法在内的第一性原理计算在研究发光材料发光机理方面具有较大优越性。本文介绍的相关计算方法可以推广至过渡金属离子（例如，Cr3+、Bi3+、Mn4+等离子）掺杂体系。

稀土发光材料理论计算研究领域的研究者们可以针对结构表征和光谱测量等实验研究工作中相关机理问题，发展或应用先进的第一性原理计算方法，设计并构造合适的几何结构模型，汇总并分析计算过程相关数据和信息，探究诸如上面提到的各类发光机理问题，从而帮助诠释实验结果、促进新材料的设计和性能优化。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220247.