线性系统的事件触发输出反馈有限时间有界控制

杨中林,魏自航,林相泽

(南京农业大学人工智能学院,江苏南京 210031)

1 Introduction

With the development of wire and wireless technologies,modern control systems have been operated by digital communication networks.In standard control books such as [1-2],periodic control is presented as the only choice for implementing feedback control laws on digital platforms.However,classical sampleddata control is based on performing sensing and actuation periodically.For a type of large-scale resourceconstrained wireless embedded control systems,it is desirable to limit the sensor and control computation and communication to instances that the system needs attention.Hence,an aperiodic digital control called event-triggered control(ETC)[3-8]has been proposed to avoid the waste of sources and the congestion of computing devices or communication networks.

Up to present,for research on event-triggered control,most existing literatures focus on asymptotical stability (AS) [9-14].It is well known that asymptotical stability of a system is a qualitative analysis over an infinite time interval.However,in many practical applications,such as missile systems,analog computer systems,active and parametric networks,the main concern is the quantitative behavior of the system over a fixed finite-time interval [15-19].In these cases,finite-time stability,which focuses its attention on the system behavior over a finite-time interval,is more practical than asymptotical stability analysis of a system.In recent years,finite-time stability was extended to finite-time boundedness (FTB) [16,18].Most of existing results focus on conventional feedback control or classical sampled-data control and FTB of dynamical systems via event-triggered control is still in its embryonic stage.

ETC scheme,which is reactive and generates sensor sampling and control actuation when the triggering condition based on current measurements is violated [6],has been widely applied to deal with many control issues,such as state or output feedback control[5,11-13,20],because it can efficiently reduce the update number of control signal so that communication resources can be saved significantly.The first important issue is that ETC schemes should guarantee a positive minimum inter-event time (MIET) which is the minimal time distance between any two consecutive event time instants.Otherwise,Zeno behaviour occurs.It was proven that for state feedback control of linear systems without external disturbances the positive MIET is guaranteed to exist [5].While,for an output feedback controller in a similar setup,the positive MIET may not exist [21].Moreover,it was theoretically proven that with arbitrary small external disturbances,the positive MIET possibly becomes zero even though it can be ensured in the absence of external disturbances[22].Hence,it is not an easy task to ensure that finite-time boundedness of the closed-loop systems in ETC output feedback scheme to avoid Zeno behaviour because for FTB,the presence of external disturbances is a indispensable part of the definition,which motivates this study.

For ETC schemes,the joint design of the feedback controller and the triggering condition is another important issue.In asymptotical stability of the closed-loop system via event-triggered control,emulation-based approaches are the common choice in practice [5,9-10,14].Hence,in this paper,an emulation-based approach is also used to consider the triggering condition with a priori that the output feedback controller is given to make the closed-loop system finite-time bounded.However,as everyone knows,the disadvantage of such an emulation-based approach is that it is impossible to obtain an optimal joint design of the feedback controller and the triggering condition[10-11].Hence,in this paper,to overcome this disadvantage,a free parameter is introduced in the design process of the triggering condition to minimize the update number of control signals while finite-time boundedness of the resultant closedloop system is still guaranteed.

Main contribution and innovation of this note are listed as follows: 1) Event-triggered output feedback finite-time bounded control for linear systems is discussed,and the ETC strategies,including the triggering condition which can be tuned by regulating a free parameter,is proposed for the first time,to the best of authors’knowledge.2)Sufficient conditions for finite-time boundedness of linear systems under eventtriggered control are presented by virtue of Lyapunovlike function.The conditions are transformed into linear matrix inequalities such that it is easy to be verified and applied.

Notations: In this paper,N,Rn,Rn×nrespectively represent the sets of natural numbers,n-dimensional vectors andn×nmatrices.The superscriptTstands for matrix transposition.λmin(·) andλmax(·) denote the minimum and maximum eigenvalues of a real symmetric matrix.

2 Problem formulation and preliminaries

Consider the following linear system:

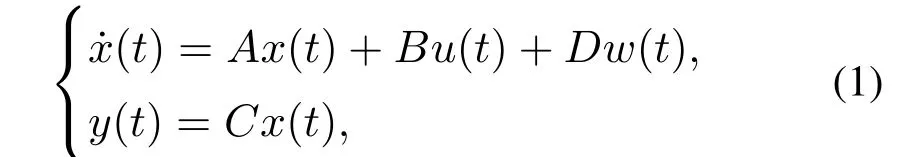
wherex(t)=[x1(t)x2(t)··· xn(t)]T∈Rnis the state,u(t)∈Rmis the control input,w(t)∈Rqis the disturbance input,y(t)∈Rpis the output signal.The matricesA,B,C,andDare system matrices with appropriate dimensions.

An observer-based state feedback controller is as follows:

In this paper,the control inputuis updated at certain instants{tk}k∈Ninstead of continuing implementation.Thus,the closed-loop system can be represented by

Letδ(t)=u(tk)-u(t)=,which can be viewed as a measure of the difference between sampled control input and continuous-time ones.Thus,the closed-loop system(3)can be expressed in terms ofandeas follows:

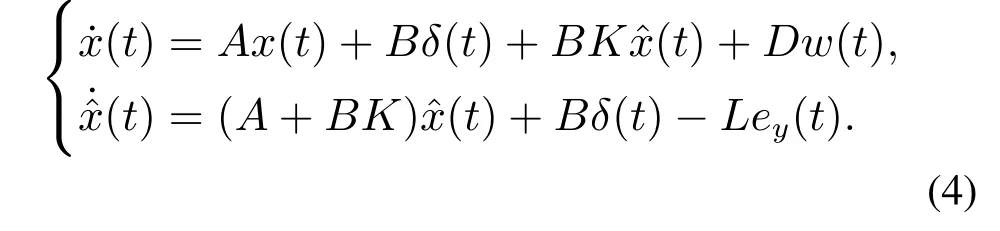
In order to discuss the event-triggered output feedback finite-time bounded control of linear systems,the following standard assumptions and definitions of finite-time boundedness,which are cited from [18-19,23-24],are listed as follows.

3 Main results

In this section,finite-time boundedness of linear system (1) via event-triggered output feedback control is to be discussed.

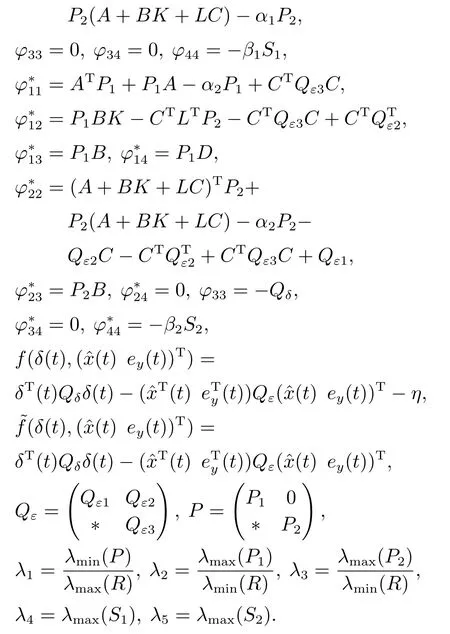
ProofThe proof procedure can be divided into two parts:

Part IUpper-bound estimation of Lyapunov-like function.

Choose a Lyapunov-like function

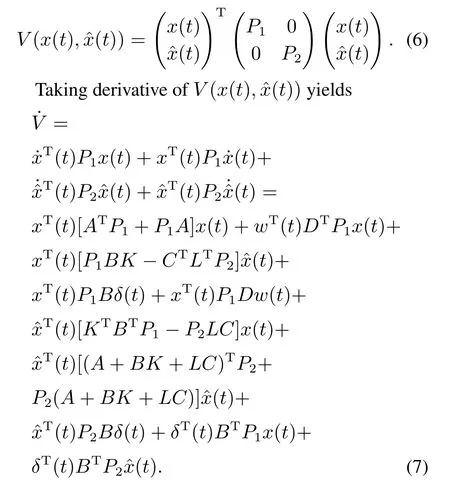
For ETC design,the event-triggered time is separated at least byTwhich is used to avoid Zeno phenomenon.During[tk,tk+T),the control is not updated.Aftertk+T,event condition determines when the control should be updated guaranteeing system performance.Hence,upper-bound estimation in[tk,tk+T)and[tk+T,tk+1)should be done respectively.

Step 1Upper-bound estimation in[tk,tk+T).

Based on(6)and(7),it yields

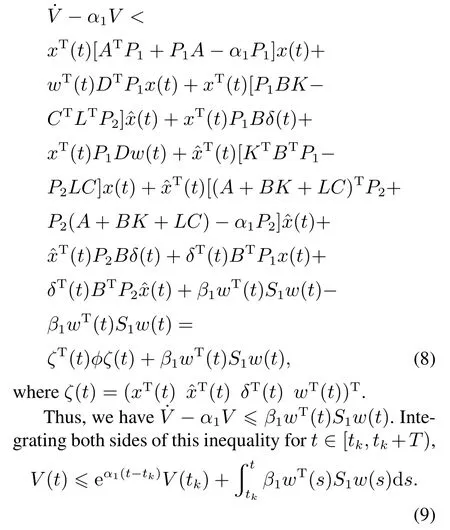
Step 2Upper-bound estimation in[tk+T,tk+1).

As that of Case 1,it is not difficult to get that

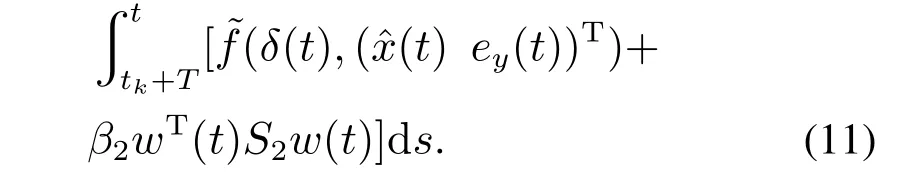
Part IIFinite-time boundedness analysis.

Using the iterative method,fort ∈(0,Tf) andt ＞tk+T,based on(9)and(11),it yields

Remark 1It is well known that asymptotic stability is a qualitative analysis but finite-time boundedness is a quantitative one,and AS of the system does not mean FTB of the system and vice visa[15,18,23].But,in the framework of event-triggered control,the difference of AS and FTB should be noted extraordinarily.For AS,the overall energy trend needs to be downward to guarantee asymptotical stability of the system,for example,during the period between two updated time such as [tk,tk+1) the energyV(x(t)) of the system is required to decline[5]or be bounded during[tk,tk+T)and comes down during [tk+T,tk+1) [11].Fig.1(a)shows the case as that in [11].During [tk,tk+T),the energyV(x(t)) of the system is only required to be bounded but not declined,the system is AS but not FTB.However,for FTB,the energyV(x(t))of the system does not need to decline,but the upper-bound estimation of the Lyapunov-like functionV(x(t)) should be known to guarantee finite-time boundedness of the closed-loop system,Fig.1(b).

Fig.1 Difference between asymptotic stable and finitetime bounded

Remark 2From Theorem 1,it is not difficult to see that the event-triggered sampling rule designed in this paper includes two parts,time condition and event condition.Time condition can effectively avoid Zeno phenomenon for the sampling time separated at least byT.Event condition is proposed to coordinately determine the next update time of control signal.It is worth mentioning that the free parameterηin event condition,which is used to coordinately regulate the number of updates of the controller,is put forward for the first time,to the best of our knowledge.

Remark 3For update ways of control signal,it is mainly affected by the adjustment of two free parameters in the event triggered sampling rules,which areTin time condition andηin event condition,respectively.In terms of the update forms of control signal,it can be divided into periodic update and aperiodic update,e.g.see Fig.5(a): aperiodicity and Fig.5(c):periodicity.On the other hand,according to the update influence of control signal on the finite-time boundedness of system,it can be regarded as effective control signal and invalid control signal.In Fig.3,for Case 1 and Case 2,the system is Un-FTB(UFTB),so the corresponding updated control signal is invalid control signal.However,for Case 3,the system is FTB,so the updated control signal at this time is the effective control signal.

4 Illustrative example

In this section,simulation results are presented to show the validity of the method proposed in this paper.

Example 1Consider the following linear system with an event-triggered output feedback controller:

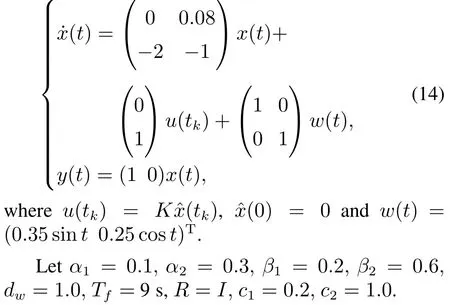
As will be readily seen from Fig.2(a),Case 1,linear system(14)is AS,but it is not FTB.To make linear system(14)FTB,letK=(3-6)andL=(-0.5-6)T.Withη=0.2,statuses of control signal are exhibited in Table 1,and responses ofxT(t)Rx(t) are shown in Fig.2.From Fig.2(a),Case 2,it can be seen that with the initial control values un-updated,linear system(14)is still not finite-time bounded,which means that control input needs more updation.If control signal updates according to an appropriate event-triggered condition,the closed-loop linear system is finite-time bounded,see it in Fig.2(a),Case 3.So,the effectiveness of the proposed method is proved.

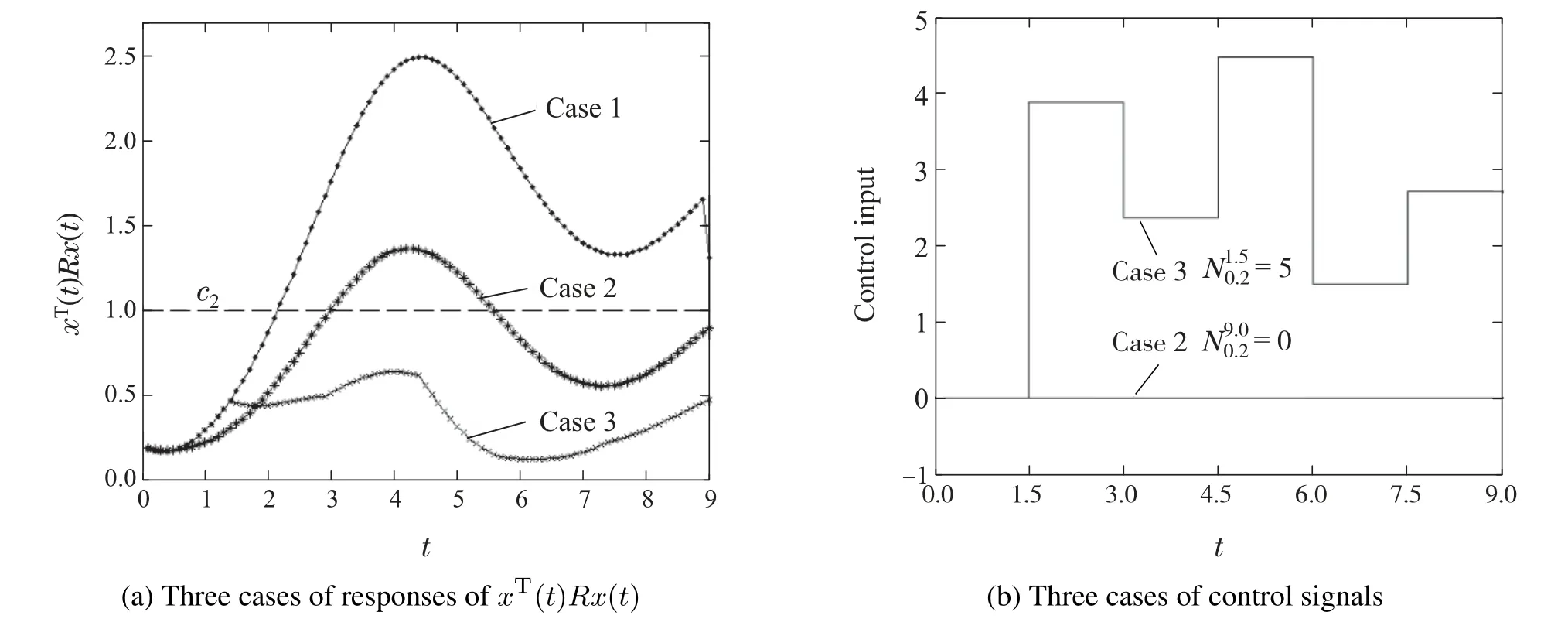
Fig.2 State response and control input

Table 1 Control signal with η=0.2

Moreover,based on numerical calculation,maximum effective values ofTandη,,can be found.For linear system(14)withK=(3-6)andL=(-0.5-6)T,=2.2 s and=17.1.Linear system (14) is FTB as long as 0＜T≤2.2 s andη≤17.1.And in Fig.3,T=1.5 s,η=0.18 andT=2.0 s,η=10 are respectively chosen.

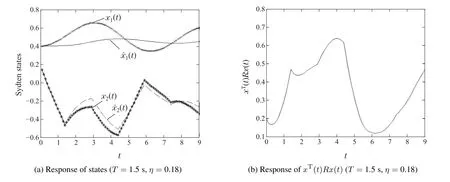
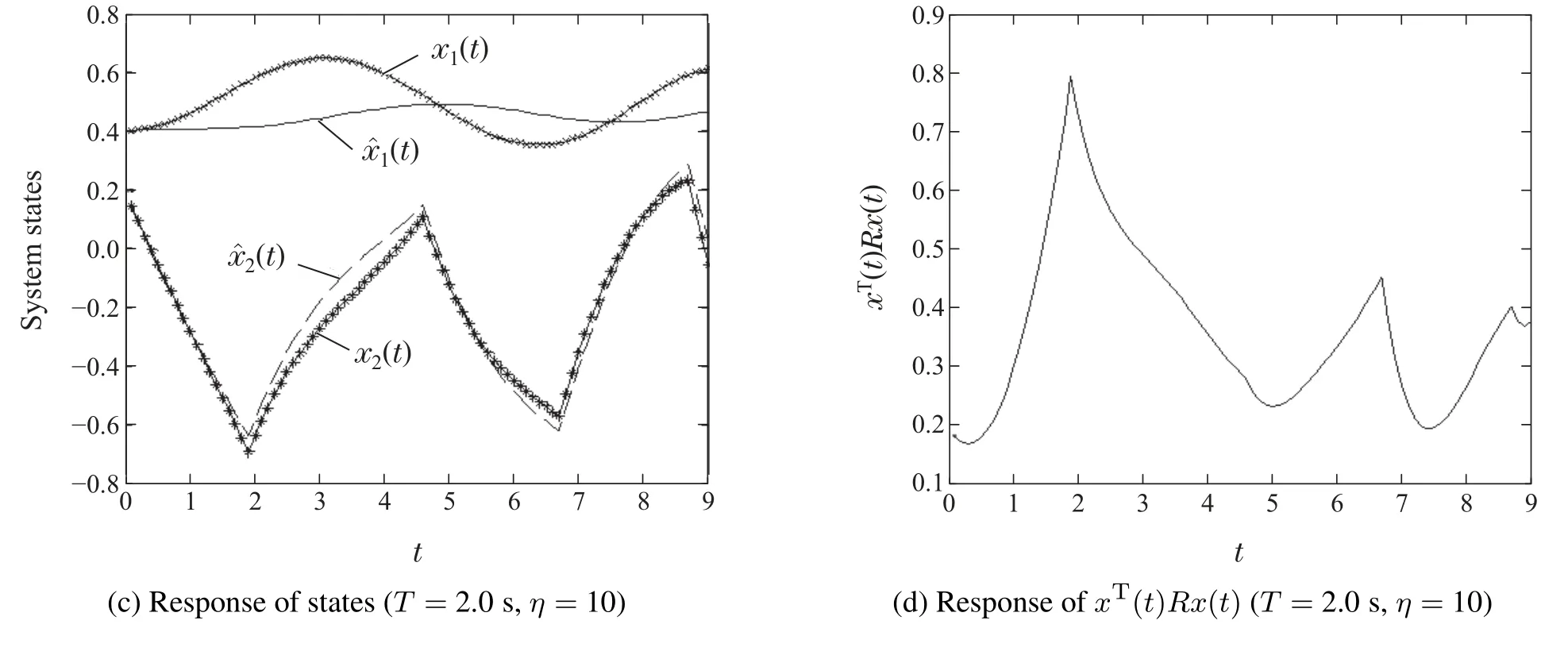
Fig.3 System response with different parameters

For linear system (14) withK=(3-6) andL=(-0.5-6)T,in case of continuous control,the system is not FTB,as shown in Fig.4(a)and Fig.4(c),but with an appropriate event-triggered control strategy,the system may achieve FTB as shown in Fig.4(b)and Fig.4(d) withT=1.0 s,η=15.On the other hand,for linear system (14),and the parametersc1,c2andKchanged to bec1=0.04,c2=1.0.andK=(0.1-10),then the system is FTB with continuous control,as shown in Fig.5(a)and Fig.5(c),but for inappropriate ETC,the closed-loop system is not FTB,as shown in Fig.5(b)and Fig.5(d).

Fig.4 State response and control input with continuous and appropriate ETC strategies

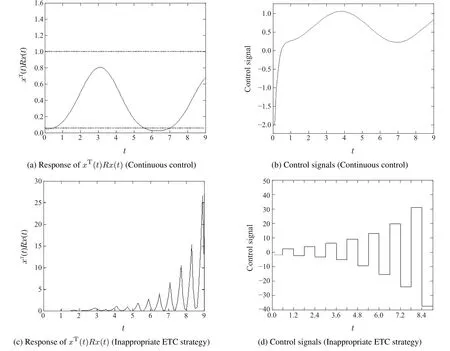
Fig.5 State response and control input with continuous and inappropriate ETC strategies

5 Conclusion

Finite-time boundedness of linear systems via event-triggered output feedback control have been addressed.Based on Lyapunov-like function,sufficient conditions have been presented to ensure FTB of the resultant closed-loop system via ETC.Moreover,an appropriate event-triggered rule with tunable parameters has been proposed to avoid Zeno behavior and to guarantee system performance.How to extend the proposed method to switched linear systems needs further research.