级联RTAC系统动态神经网络辨识与分散镇定控制

张 宇 程开新 竺俊杰 武国勋 姚熊亮

(1.青岛哈尔滨工程大学创新发展中心,山东青岛 266400;2.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨 150001;3.大连理工大学电气工程学院,辽宁大连 116024)

1 引言

具有旋转激励的平移振荡器(rotational/translationalactuator,RTAC)是研究欠驱动系统[1-2]的基准系统之一,因其具有明显的强非线性、欠驱动特性,常被用来分析设计非线性控制器,测试控制器的性能.

关于RTAC系统的控制器设计问题,很多学者已经进行了广泛的研究.期刊International Journal of Robust and Nonlinear Control对RTAC系统的非线性控制问题进行过专门的研究报道[3-4].对于RTAC系统,常见的控制设计方法有两类: 一是通过部分反馈线性化和解耦处理将系统转化为严格反馈的级联规范型,然后应用经典的反步法得到系统的稳定控制律[5-7];另外一种方法是利用RTAC的无源特性设计控制器[8-9].近期,学者们进一步挖掘了RTAC的特性,对其运动耦合增强[10]、匹配干扰下的连续控制[11]以及最大反馈线性化[12]等问题进行了研究.此外,其他一些控制算法,包括输出反馈控制[13-14]、滑模变结构控制[15-16]、自适应控制[17]、智能控制[18]也被应用于RTAC的控制器设计.

现有的RTAC系统控制研究多以单个RTAC系统作为被控对象,对多个RTAC构成的级联型RTAC系统的控制研究则鲜见报道.其中,Sun等人研究了级联RTAC的非线性耦合与鲁棒控制[19]以及基于部分状态反馈的级联RTAC镇定[20].但是关于级联RTAC系统的控制还有很多问题没有解决,如协同控制问题,集中、分散不同控制器形式对系统镇定影响,以及考虑子系统间不确定关联的鲁棒控制等问题,这些都值得进一步研究探讨.

针对现有级联RTAC系统控制研究存在的问题,为丰富级联非线性系统控制理论,本文将对基于动态神经网络辨识的级联型RTAC系统的分散镇定控制展开研究.首先,采用拉格朗日方程得到级联RTAC数学模型;然后,引入动态神经网络利用其对非线性函数的逼近能力,辨识出分散子系统间的不确定关联项,并采用考虑不确定关联项的分层滑模控制算法完成系统稳定性控制;最后,通过数值仿真验证所提分散控制系统的有效性.

2 级联RTAC数学模型

如图1所示,级联RTAC系统由n个RTAC通过弹簧柔性连接组成,对于第i(1 ≤i≤n)个RTAC,其由一个未驱动的平移振荡器(小车)和受转矩驱动的旋转偏心质量(小球)组成.小车通过弹簧连接在固定端(或第i-1和i+1个RTAC)上,在水平方向作一维直线运动,位移用xi表示,小球在作动器转矩Ni的作用下在水平面内做旋转运动,转动角度为θi.小车质量为Mi,弹簧刚度系数为ki,小球质量为mi,其转动半径为ri,小球关于质心转动惯量为Ji.

对于第i个RTAC子系统,选取小车位移xi和小球转角θi为广义坐标,此时拉格朗日方程具体形式为

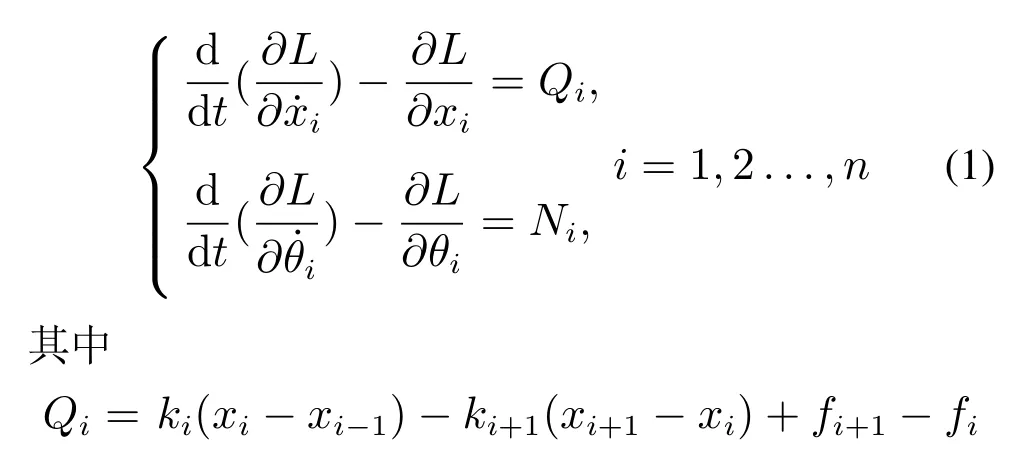
为RTACi在直线运动方向受到的非保守力.L为RTACi子系统的拉格朗日函数,fi(i=1,2,...,n)为RTAC子系统间的不确定作用力(如非线性弹性恢复力、弹簧阻尼力等未建模动态),fi同时作用在RTACi和RTACi-1两个子系统上,增强了子系统间的关联,称其为级联RTAC系统的不确定关联项,为表述简洁,将不确定关联项记为

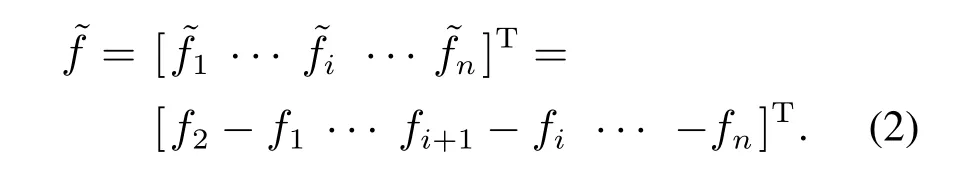
通过计算RTACi子系统的动能和势能差值得到子系统的拉格朗日函数L,代入到式(1)中,可得到RTACi子系统的数学模型,即

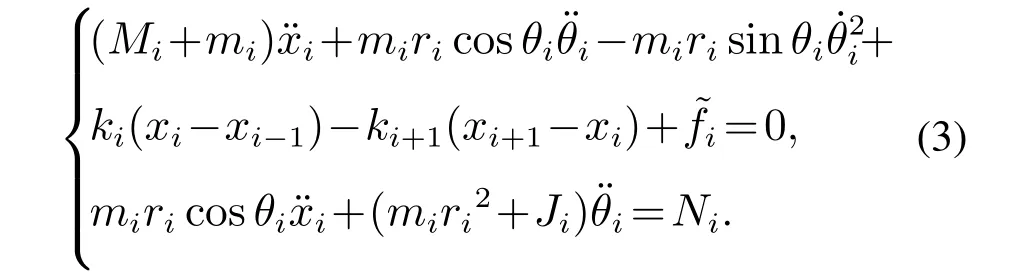
将n个RTAC的数学模型联立,可得到整个级联RTAC系统的数学模型.

级联RTAC系统每个子系统数学模型形式接近,具有相似组合系统特征,可将式(4)整理为矩阵形式

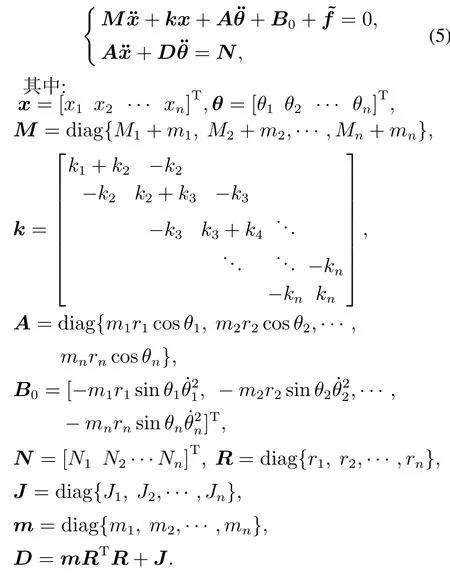
3 级联RTAC动态神经网络分散控制

3.1 分散控制

作为一种非线性关联系统的有效控制手段,分散控制的基本思想为将整个被控系统拆解为多个相互关联的子系统,以子系统的局部状态信息作为依据设计分散控制器[21-22].与集中控制相比,分散控制各子系统控制器不需要通信,可提高控制器执行效率,且各子系统控制器独立运行,增加了控制系统可靠性.为此,本文采用分散控制方法来实现级联RTAC系统的镇定控制.

不同于单个RTAC,级联RTAC系统的小车具有多级耦合特性,不确定关联项引起的建模误差在级联RTAC耦合特性影响下可在多个RTAC子系统间传递,形成误差累积;此外,级联RTAC系统具有多个振动模态,而不确定关联项与振动形式相关,在不同模态下并不相同.在无法确定不确定关联项与RTAC子系统间弹簧弹性力的相互关系时,直接对系统进行离散,将不确定关联项作为外部干扰,独立设计镇定控制器将不可避免的造成控制精度低的问题.因此,开展分散控制时,对级联RTAC系统的不确定关联项进行辨识是必要的.

3.2 动态神经网络辨识

在级联RTAC系统的分散控制系统设计中,如何处理RTAC子系统间的不确定关联项,是保证分散控制系统控制效果的关键.为此,本部分引入动态神经网络(dynamic neural network,DNN),利用神经网络对任意连续有界非线性函数的一致逼近能力,辨识出级联RTAC中的不确定关联项,并以此为基础,完成级联RTAC系统的分散控制器设计.

因动态神经网络存在时间相关环节,在处理动力学系统的辨识问题时,其动态性能较静态网络更具优势[23-24].动态神经网络辨识具体实现方法如下.

将级联RTAC系统数学模型整理为如下形式:

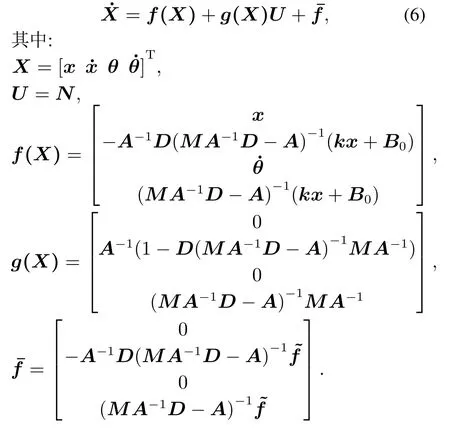
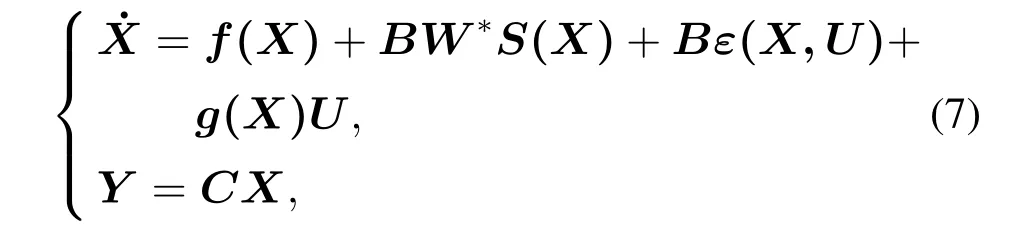
其中: 状态变量X维数为4n,B为4n×r矩阵,C为q×4n矩阵,W*为r×4n维神经网络权值矩阵,ε(X,U)为系统误差项,满足‖ε(X,U)‖＜θ*,θ*＞0为未知常数.S(X)为光滑、至少二次可微单调递增函数组成的4n维向量,此处选用Sigmoid函数,形式为

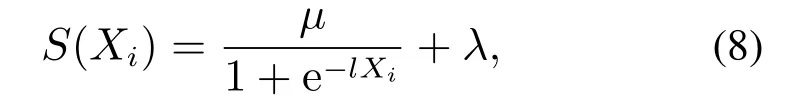
其中:μ和l为有界参数,λ为常数,Xi(i=1,2,···,4n)为系统状态变量.

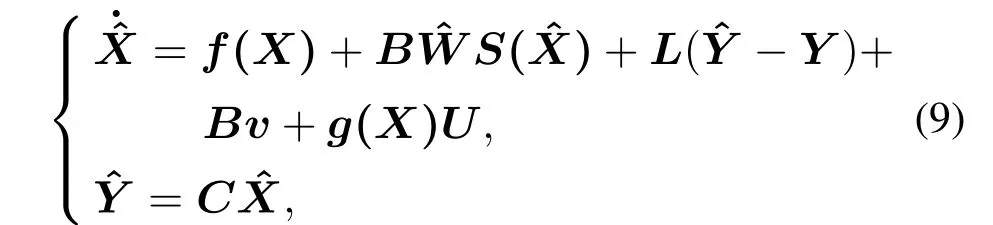
其中,选取适当的L,使得Ac=LC为稳定矩阵,且使(Ac,B)构成可控对,此时,如果存在q×r矩阵F,使H(s)=FTC(sI -Ac)-1B为一严格正实函数矩阵,则一定存在一个4n×4n阶正定矩阵P满足

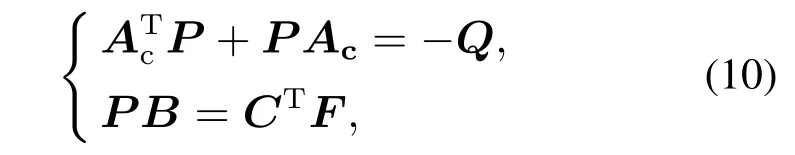
其中Q为任意4n×4n阶正定矩阵.需要注意的是,本问题中系统状态均为可测量的,DNN的主要目标为不确定关联项的辨识.DNN突触连接权值采用如下自适应律进行在线调整,以实现对不确定关联项的在线辨识.

关于上述动态神经网络对级联RTAC系统中不确定关联项辨识误差的收敛性,存在如下定理.

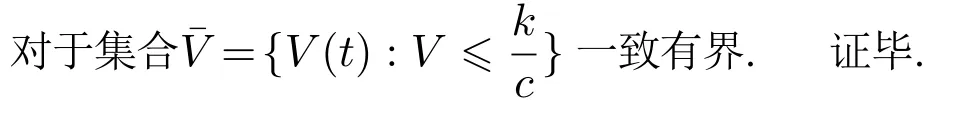
3.3 分层滑模分散镇定控制

首先为RTACi设计如下一级滑模面,两个滑模面分别对应RTACi子系统的振子平移运动和旋转激励旋转运动.

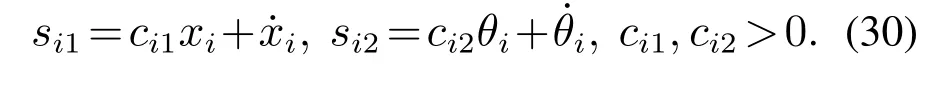
若系统状态能达到一级滑模面,当在一级滑模面上运动时,系统状态满足:=0,RTACi子系统的小车位移和小球旋转角度均按指数收敛到零.

考虑到RTAC系统的欠驱动特性,单个控制输入Ni无法同时对两个独立变量si1和si2进行直接控制,为保证RTACi子系统的一级滑模面能够到达,仍需为其设计二级滑模面,构造如下线性二级滑模面:

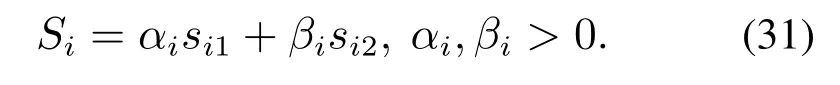
为得到使RTACi子系统二级滑模面稳定的滑模控制律,为其选取如下Lyapunov函数:

当且只当Si=0时,式(38)中的等号成立.由式(38)可知Vi(t)≤Vi(0)-≤Vi(0),即Vi(t)有界,根据Lyapunov 稳定性理论与LaSalle’s不变集原理,可知Si可稳定收敛于系统的不变集,即零点.要证明RTACi子系统的小车位移和小球旋转角度也稳定收敛到零,还需要对一级滑模面的稳定性进行证明,具体证明过程见附录A.

4 数值分析

通过数值仿真分析本文所提级联RTAC系统控制方案的控制效果.在数值仿真过程中,设定n=3,即级联RTAC系统包含3个RTAC子系统.每个RTACi子系统取相同参数,具体取值如表1所示.

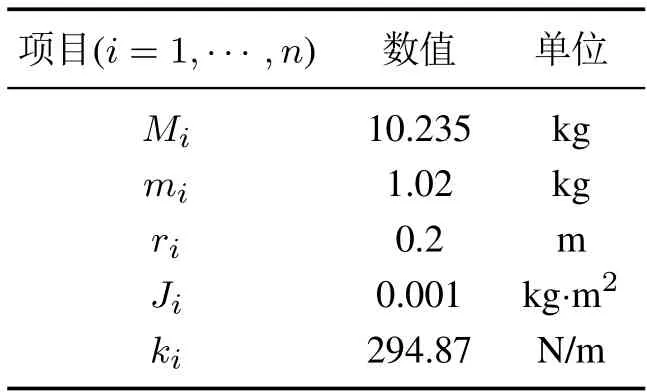
表1 级联RTAC系统参数Table 1 System parameters of cascade RTAC

对于n=3的级联RTAC系统,其在固定住小球转角时,可视为三自由度振动系统,在不考虑不确定作用力(如非线性弹性恢复力、弹簧阻尼力等未建模动态)的影响时,其有三阶振动模态.级联RTAC系统小车的各种运动均可表示为3种振动模态的线性组合,如果能对3种振动模态进行有效控制,即可实现级联RTAC系统任意平移振动的有效控制.

为了验证基于动态神经网络辨识的级联RTAC系统分散控制器的有效性,对3种不同工况下的RTAC系统镇定控制以及不确定关联项辨识进行了分析.3种工况对应n=3的级联RTAC系统的三阶振动模态.以三自由度振动系统的振型向量为基础,以第2个RTAC子系统小车初始位移为基准进行归一化,确定不同工况下各RTAC 子系统中小车的初始位移.通过调整各RTAC子系统中小车的初始位移,可以控制级联RTAC系统进入哪种振动模态.3种工况对应的初始条件如表2所示.

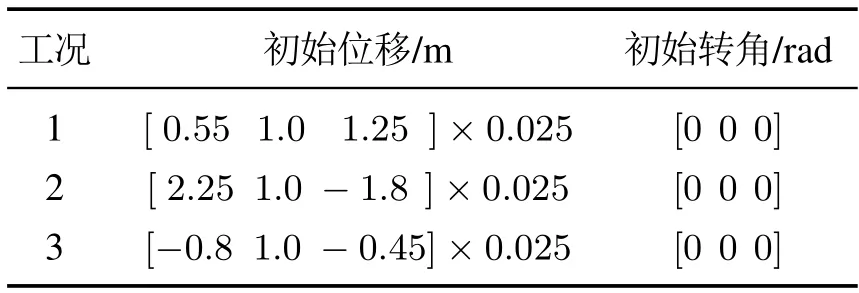
表2 各工况初始条件Table 2 Initial conditions of simulations

仿真中不确定关联项采用正弦函数形式,即˜f=Asinωt,在3种工况下各RTAC子系统的不确定项幅值均取0.1 N,频率分别取级联RTAC系统的三阶共振频率,即2.38 Hz,6.69 Hz以及9.67 Hz.分别对无控、分层滑模分散控制(hierarchical sliding mode decentralized control,HSMDC)以及基于动态神经网络的分层滑模分散控制(dynamic neural network based hierarchical sliding mode decentralized control,DNN-HSMDC)3种不同条件下的级联RTAC小车位移响应和不确定关联项辨识情况进行了分析,数值结果见图2-7.

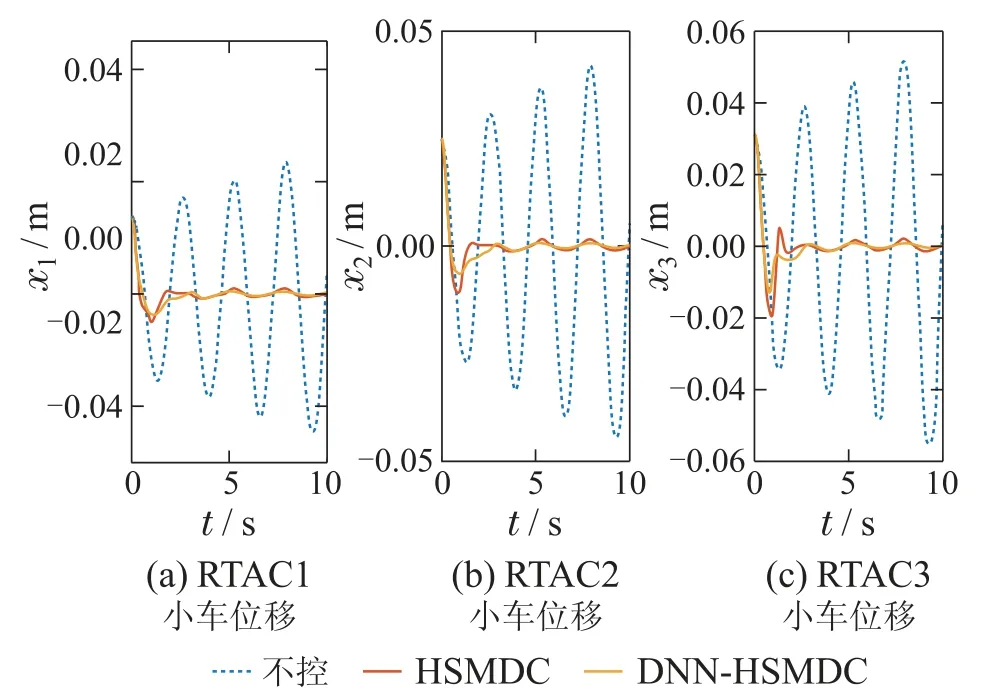
图2 工况1: 一阶振动模态下RTAC小车位移响应Fig.2 Simulaiton1:displacement responses of RTAC in first vibration mode

如图2所示,在一阶振动模态下,因不确定干扰项频率与系统一阶共振频率一致,向级联RTAC系统注入能量,导致无控条件下3个小车的位移响应幅值逐渐增大,而施加HSMDC和DNN-HSMDC控制后,小车位移很快稳定到原点附近.在观测时间[0,10]s内,HSMDC控制使3个小车的位移均方根值分别降低了84.5%,83%和81%;DNN-HSMDC控制则分别降低了85%,84.3%和83.6%.可以看出DNN-HSMDC控制效果要优于HSMDC,这是因为DNN-HSMDC引入神经网络对级联RTAC系统中的不确定关联项进行辨识,补偿了建模误差,得到了更加准确的被控对象模型,进而提升了控制效果.

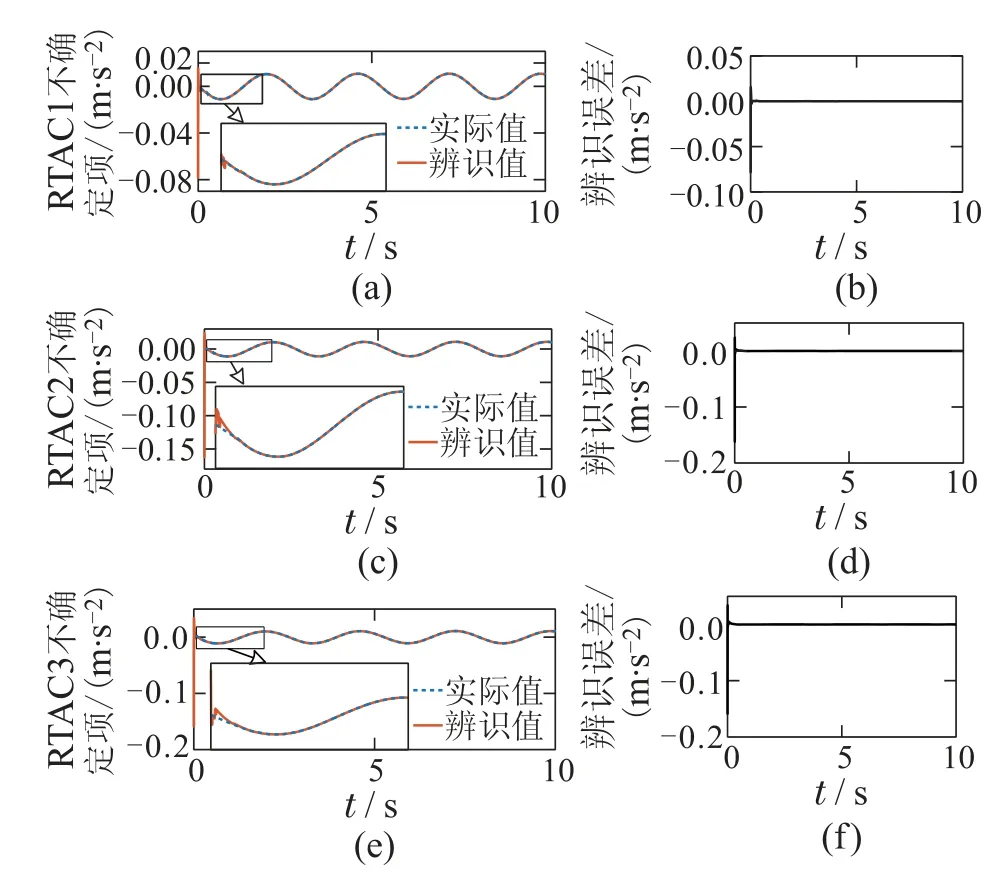
图3 工况1: 一阶振动模态下不确定关联项辨识结果Fig.3 Simulaiton1: identification results of uncertain interconnected forces in first vibration mode

为比较不同控制算法的瞬态控制效果,采用单周期位移峰值衰减率作为瞬态性能评价指标,即从仿真开始到小车振动一个周期结束时,小车位移峰值相较于不控时的衰减比例.因为施加控制前后,小车运动周期维持不变,故单周期位移峰值衰减率可体现控制器对振动的抑制快慢.相较于不控时,HS-MDC控制下的3个小车的单周期位移峰值衰减率分别为94.8%,97.3%,86.5%;而DNN-HSMDC控制下单周期位移峰值衰减率可达95.1%,98.3%,95%,可见DNN 辨识引入对振动控制系统瞬态性能也有提升.

如图4-7所示,对于二阶振动模态和三阶振动模态下的级联RTAC系统镇定控制,可得出与工况1类似的结论.不同工况下,基于动态神经网络辨识的分层滑模分散控制均能实现对级联RTAC系统不确定关联项的准确辨识,并能实现小车位移响应的有效镇定,且控制效果要优于无辨识环节的HSMDC控制.

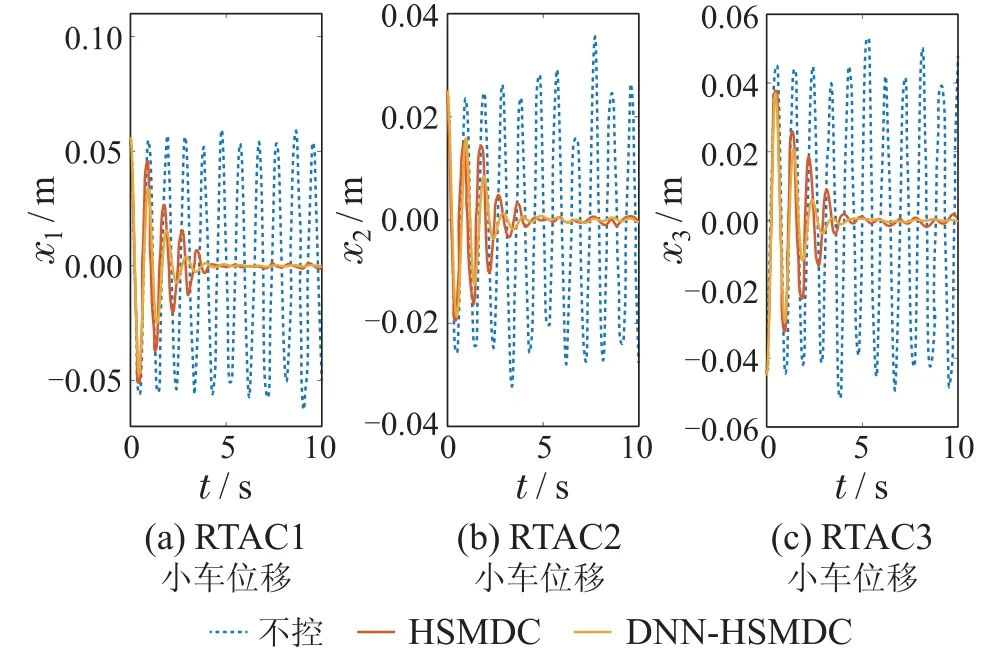
图4 工况2: 二阶振动模态下RTAC小车位移响应Fig.4 Simulaiton 2: displacement responses of RTAC in second vibration mode

工况2中,HSMDC对3个小车控制效果(位移均方根降低量)分别为63.7%,68.6%和65.5%,稳态误差为[1.5 1.1 1.9]×10-3m,单周期位移峰值衰减率为18.3%,31.7%,28.5%;DNN-HSMDC 控制效果为70.9%,71.7%和70.3%,稳态误差为[0.37 0.34 0.25]×10-3m,单周期位移峰值衰减率为41.4%,47.9%,37%.

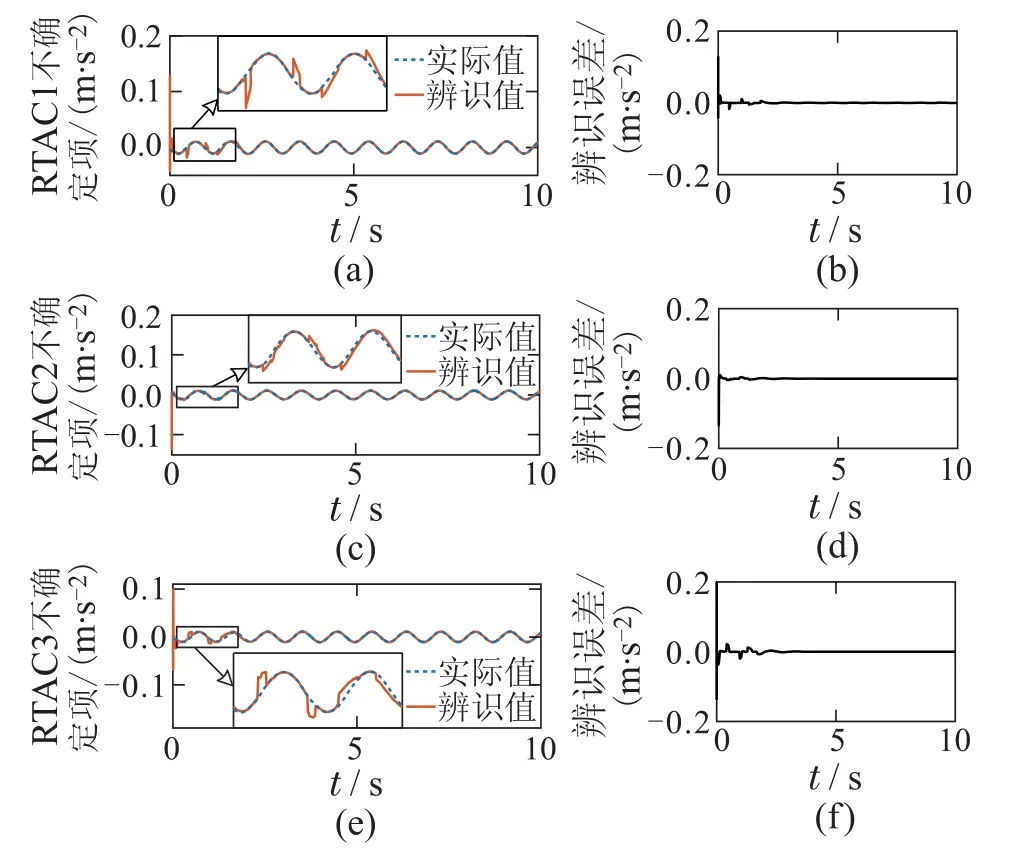
图5 工况2: 二阶振动模态下不确定关联项辨识结果Fig.5 Simulaiton 2: identification results of uncertain interconnected forces in second vibration mode

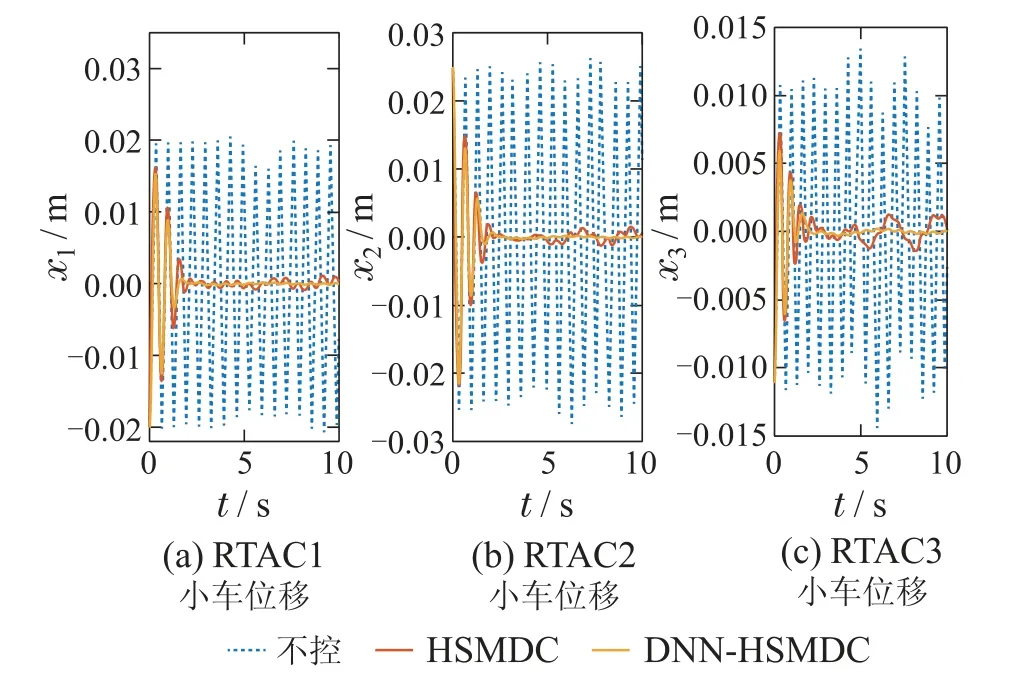
图6 工况3: 三阶振动模态下RTAC小车位移响应Fig.6 Simulaiton 3: displacement responses of RTAC in third vibration mode

工况3中,HSMDC对3个小车控制效果(位移均方根降低量)分别为74%,75.1%和77.3%,稳态误差为[1.1 1.5 1.5]×10-3m,单周期位移峰值衰减率为30.5%,37.3%,44.4%;DNN-HSMDC控制效果为76%,76.4%和80.7%,稳态误差为[0.12 0.11 0.13]×10-3m,单周期位移峰值衰减率为37.2%,47.4%,48.3%.在工况2和工况3中,DNN辨识环节的引入对控制效果的提升要比工况1更加明显.

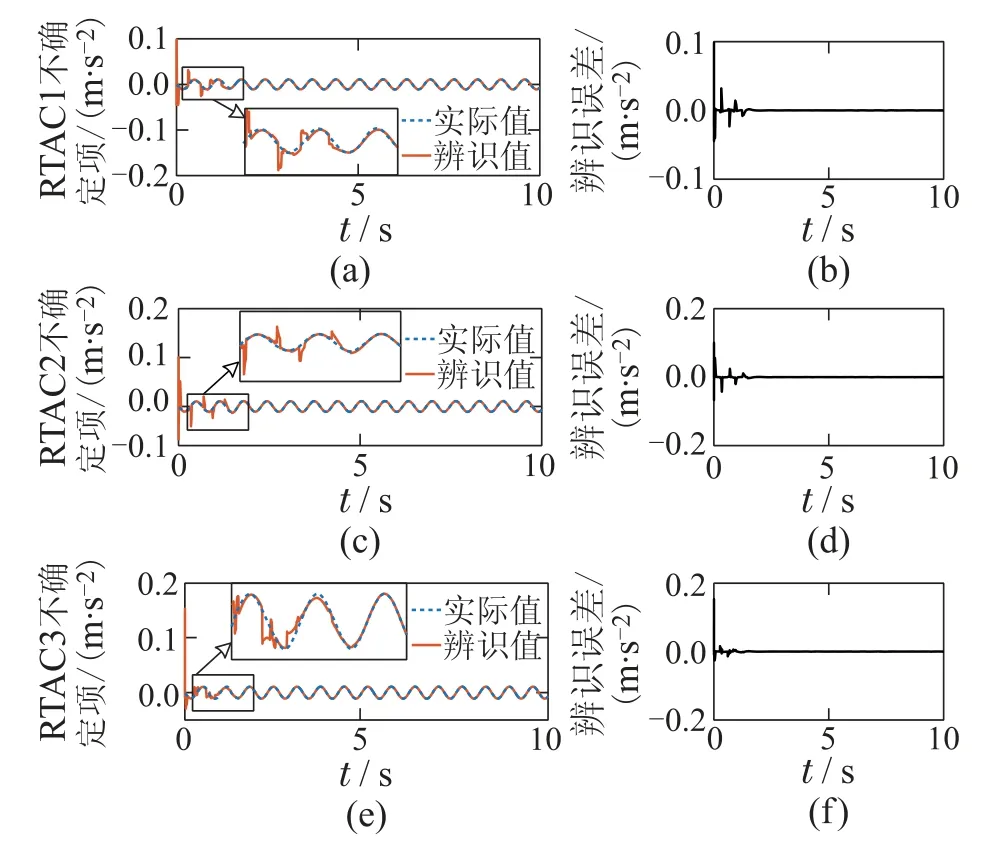
图7 工况3: 三阶振动模态下不确定关联项辨识结果Fig.7 Simulaiton 3: identification results of uncertain interconnected forces in third vibration mode

5 结论

本文提出了一种基于动态神经网络辨识的级联RTAC系统分散控制方案.引入动态神经网络辨识出分散子系统中的不确定关联项,并采用分层滑模控制算法为级联RTAC系统设计了分散控制器,通过理论分析给出了动态神经网络辨识误差一致有界的条件,证明了闭环分散控制系统的稳定性.数值仿真表明,基于动态神经网络辨识的分层滑模分散控制能实现对级联RTAC系统不确定关联项的准确辨识,可补偿系统建模误差,进而在系统位移响应抑制以及控制精度方面均优于无辨识环节的分层滑模分散控制.

附录A RTACi子系统一级滑模面稳定性证明

只有两级滑模面稳定性均得到证明,才能保证RTACi子系统镇定能够实现.现对如下一级滑模面的稳定性定理进行证明.

综上可得σ1∈L2,σ2∈L2.两个一级滑模面均为平方可积函数,且其导数有界,根据Barbalat引理即可证得两个一级滑模面是渐近稳定的.