输出非对称死区的非严格反馈非线性系统控制

孙 猛,杨 洪

(1.江苏海洋大学电子工程学院,江苏连云港 222005;2.江苏海洋大学计算机工程学院,江苏连云港 222005)

1 引言

在日常生活中,绝大多数物理系统为非线性系统,如:近空间飞行器系统[1]、无人直升机系统[2],因此,近些年来,学者们更加重视对非线性系统的研究.

一方面,基于逼近的自适应反步法作为非线性系统的一种研究方法得到了学者们的关注,并且在此研究领域中,学者们取得了大量的研究成果[3-8].文献[9]借助反步法,解决了具有未建模动态的严格反馈时滞系统的自适应模糊控制问题.文献[10]利用径向基函数神经网络(radial basis function neural networks,RBFNNs)和跟踪微分器实现对未知函数和虚拟量导数的逼近,通过反步法研究了未知控制方向的不确定系统.为了解决传统反步法中存在的参数爆炸问题,文献[11]基于反步法提出了动态面控制.动态面控制需要在反步法设计中的每一步引入一个一阶滤波器.文献[12]使用了动态面控制和反步法,利用RBFNNs逼近未知函数,研究了一类具有输入饱和的未知非线性系统自适应控制问题.然而,上述文献研究内容针对的均是严格反馈的非线性系统,相比严格反馈系统,非严格反馈系统更具一般化,控制器设计问题上也更加复杂,所以上述文献所使用的研究方法有待进一步提升或改进.

另一方面,死区经常出现在实际系统中,如液压伺服系统[13]、机器人系统[14].死区的发生会降低系统性能,造成系统的振荡,甚至使系统不稳定.目前有许多文献记录输入死区相关研究[15,18,20],但是,在实际系统中,系统输出也会出现死区情况.文献[16]针对具有输出非对称死区和状态含时滞的严格反馈系统,采用一种光滑模型描述死区,并设计了稳定的自适应模糊控制器.文献[17]针对具有输出对称死区的非严格反馈系统,通过动态面控制方和反步法,设计了一种稳定的自适应神经网络控制器.然而,上述文献内容忽略了对输出非对称死区非严格反馈系统的研究.

受到上述文献研究内容的启发,本文针对具有输出非对称死区的非严格反馈非线性系统,设计一种自适应神经网络控制器.本文主要的创新之处如下:

1) 由于在实际系统中,系统的输出死区大多是非对称形式,如在机器人系统中,机械执行关节间存在动态摩擦,会使机器人存在输出非对称死区.因此,在文献[17]的基础上,本文考虑具有输出非对称死区的非严格反馈系统.相较于输出对称死区,输出非对称死区更具一般性和广泛性,也更具实际工程研究价值;

2) 由于含未知控制方向的情况普遍存在于实际物理系统中,如船舶航向控制系统,所以,本文在文献[17]的基础之上,考虑系统状态含未知控制方向的情况.研究系统控制方向对解决现实控制问题具有一定的价值.

2 系统描述及预备知识

2.1 系统描述

考虑下面的非严格反馈非线性系统:

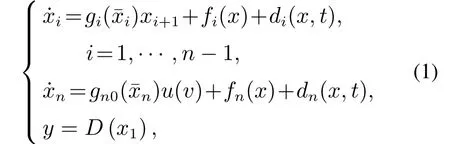
其中:x=[x1··· xn]T∈Rn,=[x1··· xi]T∈Ri,i=1,···,n表示系统的状态向量;y ∈R表示系统的输出;v(t)∈R和u(v)分别表示控制器的输入和系统的输入;di(x,t)表示有界的外部扰动信号;fi(x)是未知的光滑非线性函数,其中fi(0)=0;gi(·),gn0(·)是未知参数;D(x1)表示输出死区函数.

2.2 输出死区模型

本文考虑的输出为非对称死区[16],其模型如下:

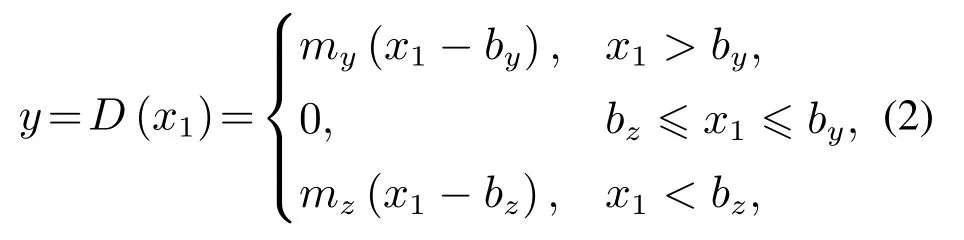
其中:mz ＞0和my ＞0分别表示死区函数的左右斜率;bz ＜0,by ＞0,|by-bz|表示死区宽度.

基于输出死区的描述,式(2)可以写成

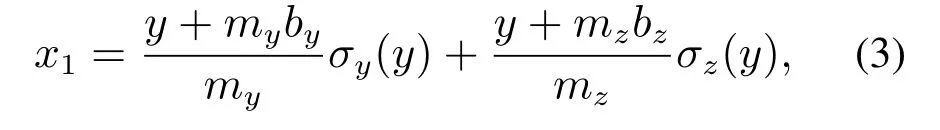
其中:σy(y)=(π+2 arctan(ky))/2π;σz(y)=(π-2 arctan(ky))/2π,k ＞0为可调参数.式(3)表示对输出死区求逆的结果,通过改变k值大小,从而可以使用该光滑模型表示式(2)中的非线性死区.

定理1的证明和文献[16]中的定理1证明类似,因此在此省略证明过程.

2.3 输入饱和模型

本文考虑的输入具有饱和特性[20],其模型如下:

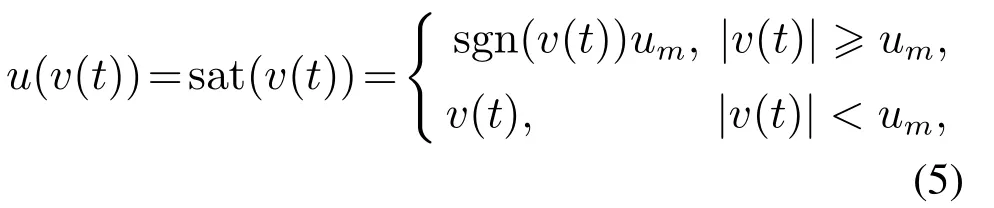
其中um是u(v)边界,当v(t)值为|um|时,u(v(t))不可微,可采用一种光滑模型逼近输入饱和函数

系统(9)的控制目标是设计的控制器v能够使系统的输出y(t)很好地跟踪给定参考的理想信号yr,即跟踪误差要满足|z1(t)|=|y(t)-yr|≤kz1,kz1为正常量,并保证闭环内所有信号是半全局一致最终有界.

为了进行控制器设计,现做出如下假设.

注2本文中的假设借鉴了文献[12,17,19,21-22]中的相关假设,说明本文做出假设的合理性.

2.4 Nussbaum函数

定义1一个连续可导的函数N(ζ),如果满足

2.5 径向基函数神经网络

对于任意定义在紧集Ωz ∈Rq上的非线性连续函数f(Z),可以由RBFNNs进行逼近[23]

3 自适应神经网络控制器设计和稳定性分析

为了简化表达,首先定义下面符号:

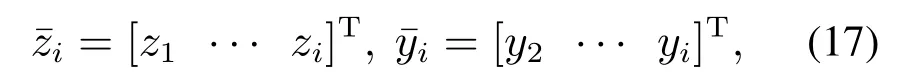
其中i为不大于n的正整数.

基于动态面控制技术,现引入如下的坐标变换:

其中:i=2,···,n;zi为误差面;ωi为一阶滤波器输出信号;yi为有界层误差;αi为虚拟控制信号.构造虚拟控制信号αi和

注4引理2说明了系统全状态可以通过变量分离的方法分离成一系列光滑函数,由假设4可以看出,包含系统全状态的未知函数也可以分离成一系列光滑函数.

3.1 控制器设计

本小节中,基于反步法的动态面控制技术将被用于处理非严格反馈非线性系统(9),设计的步骤如下.

步骤1根据式(4)(9)(18),对z1进行求导得到

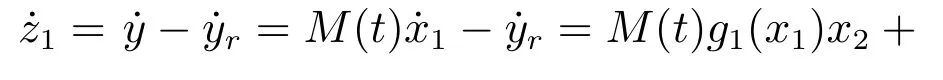
其中bn为正常量.

3.2 稳定性分析

本小节的主要目的是对所设计的神经网络控制器进行稳定性分析.首先,准备如下工作,定义下面紧集:

其中p,B0为正参数.

构造如下Lyapunov函数:

根据式(16),Young不等式,可以得到

4 仿真算例

本节通过两个数值模拟例子,验证本文所设计神经网络控制器的有效性.

例1考虑下面非严格反馈非线性二阶系统:

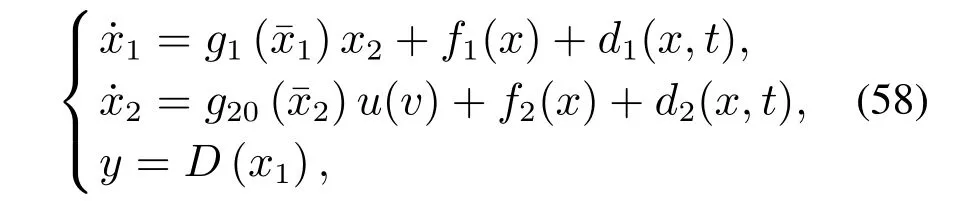
被控对象(58)的仿真参数选取表1所示.

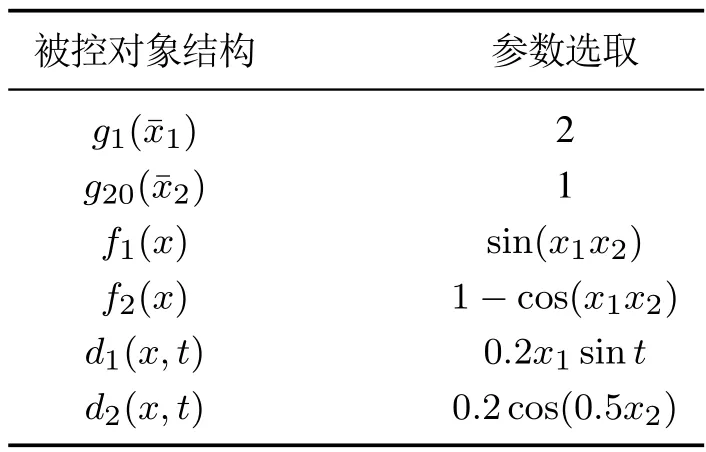
表1 被控对象(58)结构取值表Table 1 Value table of the controlled object(58)

本例中yr=0.3 sint.虚拟控制信号α2通过式(21)计算得到,其中选取a1,k1分别为2,2.其余参数取值如下:x1(0)=0,x2(0)=0.2,ω2(0)=0,θ(0)=0.5,ζ(0)=1,k2=5,a2=2,h0=0.1,σ=0.05,η=100,κ2=0.001,kz1=0.15.

在本例中,输出非对称死区y=D(x1)是由式(59)计算得到

图1是输出非对称死区y的跟踪效果及其跟踪误差图,从图中可以看出在本文所设计控制器的控制下,y可以很好地跟踪给定参考信号yr,且跟踪误差z1可由约束|kz1|控制,说明系统具有良好的跟踪性能.自适应参数θ和控制信号v(t)的有界性如图2-3所示.虚拟控制信号α2,滤波信号ω2以及它们之间的误差y2如图4所示.

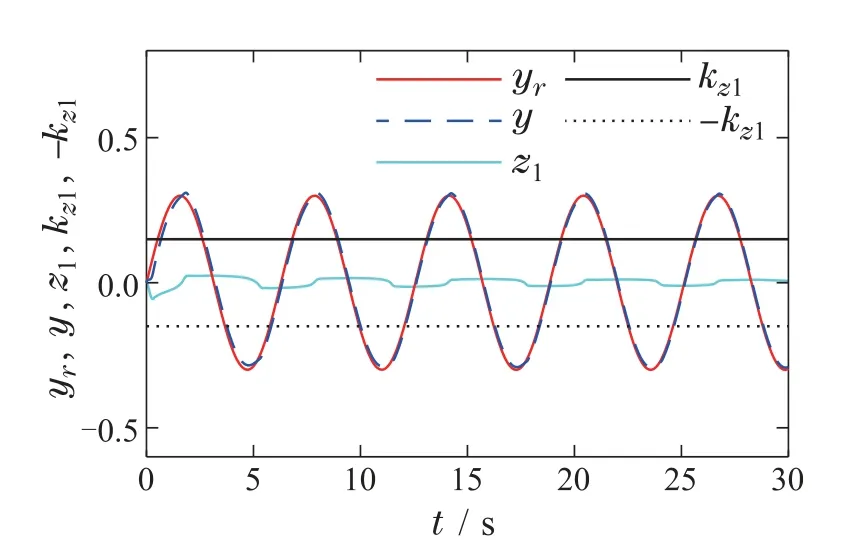
图1 输出y的跟踪效果和跟踪误差Fig.1 The tracking effect and tracking error of output y

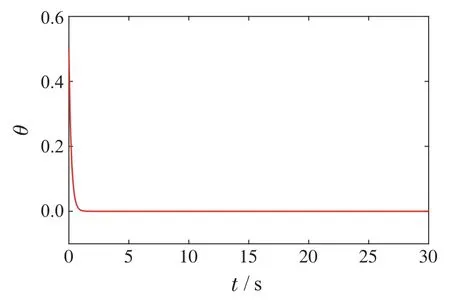
图2 自适应参数θ轨迹Fig.2 The trajectory of adaptive parameter θ

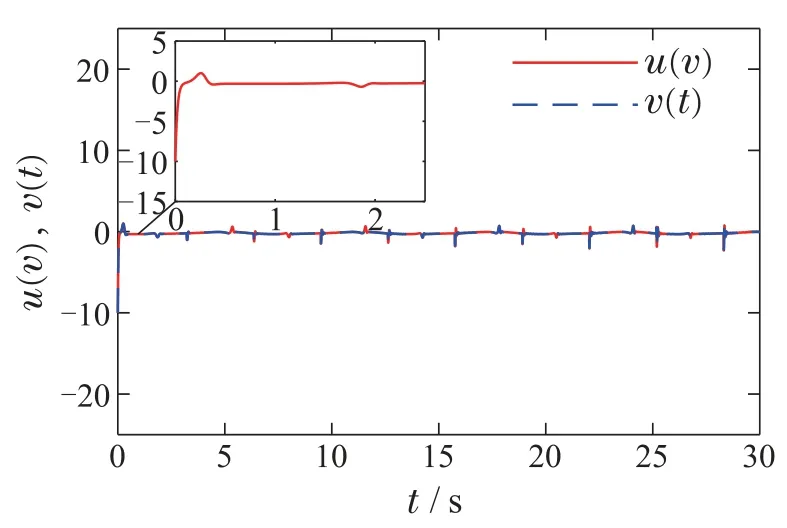
图3 控制输入v和饱和输入u(v)Fig.3 Control input v and saturation input u(v)

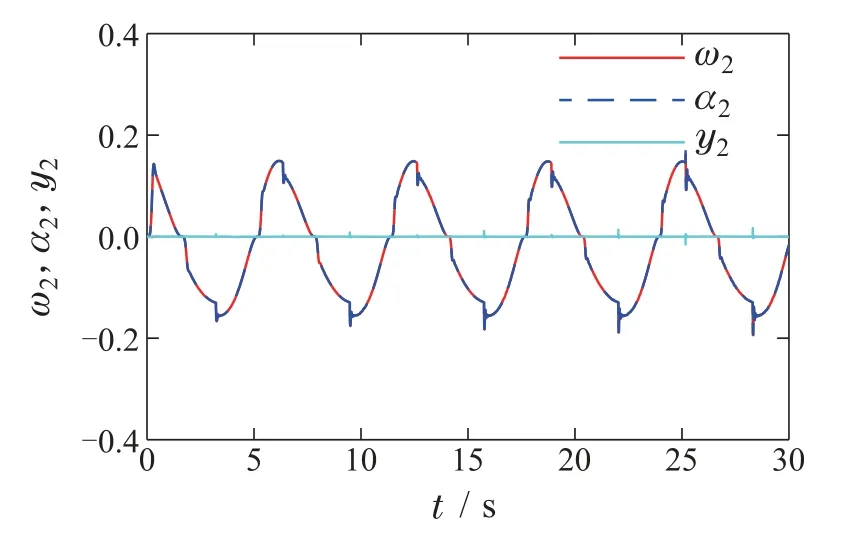
图4 虚拟信号α2,滤波信号ω2及有界层误差y2的轨迹Fig.4 The trajectories of virtual signal α2,filter signal ω2 and boundary layer error y2

例2考虑下面可以描述化学反应的简化Brusselator模型[17]:

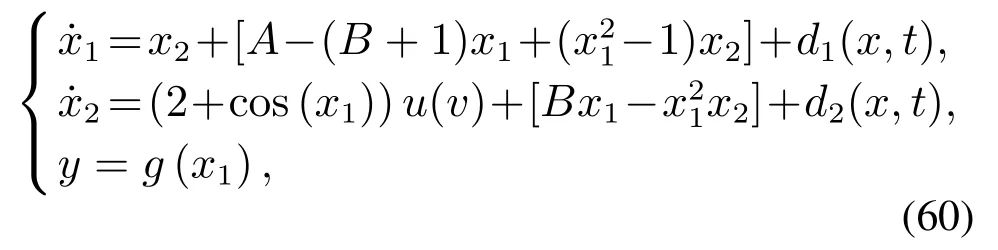
其中x1,x2代表反应中间产物的浓度.储存化学品的供应用A和B来表示,A ＞0,B ＞0.g(x1)表示输出对称死区.文献[17]中指出,Brusselator模型是一种可在一系列近似之后,从部分差分方程中推导出来的简化化学模型.所以,在实际的化学反应中,难以避免存在数学建模误差和其他类型的未知非线性.因此,系统的输出难免存在输出非对称死区的情形.基于此,本仿真考虑实际化学反应过程中,系统输出为非对称死区的Brusselator 模型,形式如下:

其中D(x1)为输出非对称死区.本文选取A=1,B=3,那么被控对象(61)的仿真参数选取则如表2所示.

表2 被控对象(61)结构取值表Table 2 Value table of the controlled object(61)

本例所选取的参考信号为yr=0.5 sint+3.虚拟控制信号α2通过式(21)计算得到,其中选取a1,k1的值分别为7,10.其余参数选取值如下所示:

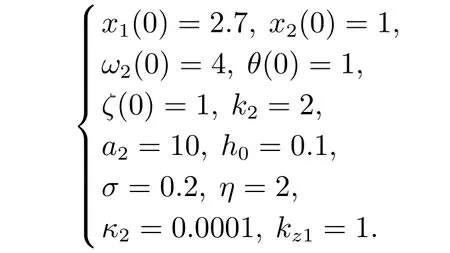
在本例中,输出非对称死区y=D(x1)是由式(62)计算得到

图5是输出非对称死区y的跟踪效果及其跟踪误差图,从图中可以看出y可以很好地跟踪给定参考信号yr,且跟踪误差z1可由约束|kz1|控制,说明系统具有良好的跟踪性能.自适应参数θ和控制信号v(t)的有界性如图6和图7所示.虚拟控制信号α2,滤波信号ω2以及它们之间的误差y2如图8所示.仿真结果表明,在实际仿真案例中,本文所设计的控制器同样满足要求.

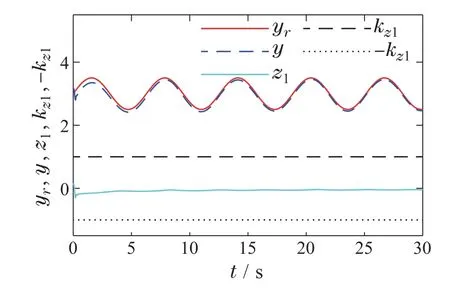
图5 输出y的跟踪效果和跟踪误差Fig.5 The tracking effect and tracking error of output y

图6 自适应参数θ轨迹Fig.6 The trajectory of adaptive parameter θ

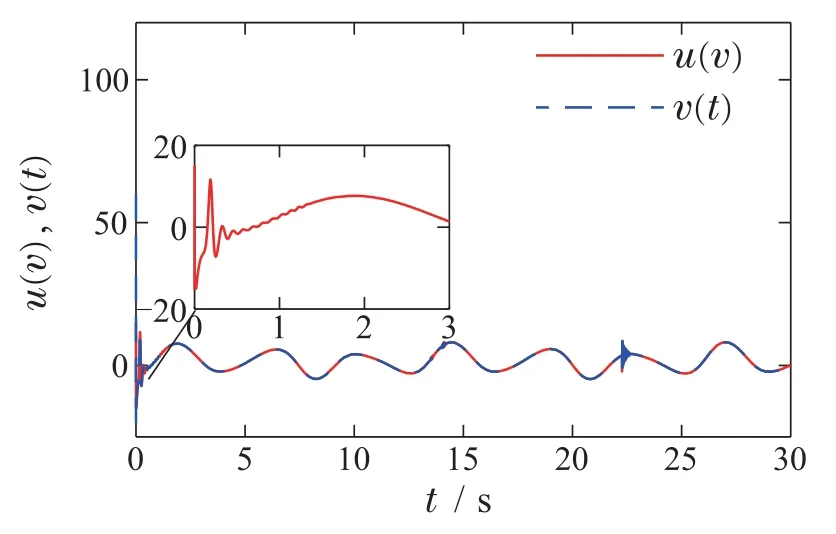
图7 控制输入v和饱和输入u(v)Fig.7 Control input v and saturation input u(v)

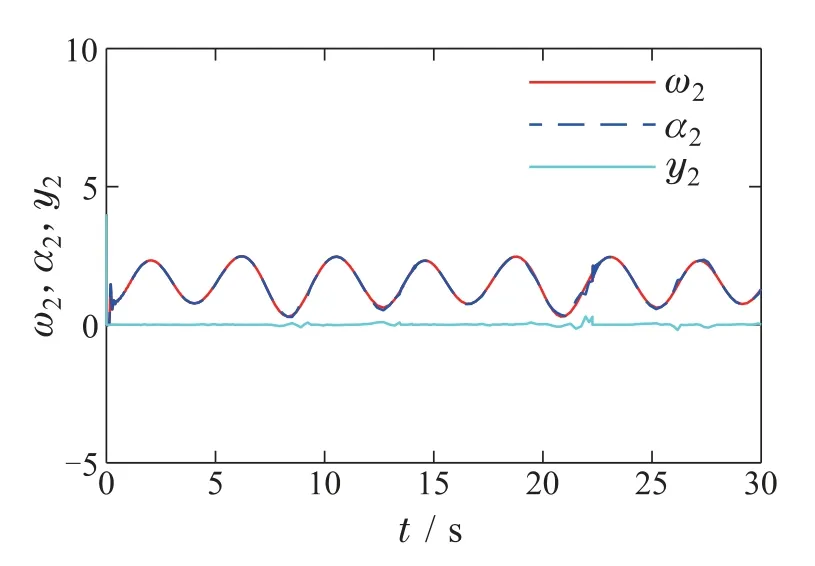
图8 虚拟信号α2,滤波信号ω2及有界层误差y2的轨迹Fig.8 The trajectories of virtual signal α2,filter signal ω2 and boundary layer error y2

5 结论

本文研究了具有输出非对称死区和状态含未知控制方向的非严格反馈非线性系统,设计了自适应神经网络控制器.针对非对称死区,采用基于死区逆的光滑逼近模型进行表示,并将此模型代入控制器的设计中.针对状态含未知控制方向,做出限制未知控制方向的假设,并设计含未知控制方向的虚拟控制信号和实际控制器.通过Lyapunov稳定性分析证明了闭环系统内所有信号半全局一致最终有界,且跟踪误差满足约束条件.仿真结果表明了所设计控制器的有效性.