基于可调谐二极管激光吸收光谱的气池光程可溯源测量

龙江雄，张玉钧，邵 立，叶 庆，何 莹，尤 坤，孙晓泉

1. 国防科技大学脉冲功率激光技术国家重点实验室，安徽 合肥 230037 2. 先进激光技术安徽省实验室，安徽 合肥 230037 3. 中国科学院合肥物质科学研究院，安徽 合肥 230031

引 言

在碳中和的国际大背景下，精确可靠地定量测量大气温室气体浓度是实现碳中和的有利手段，开发测量结果可直接溯源至国际单位制SI的气体分析仪对温室气体浓度的精确可靠监测具有重要意义。利用红外激光光谱技术结合计量学溯源方法可在不使用标准气体校准的情况下实现测量结果直接溯源至SI。

可调谐二极管激光吸收光谱(TDLAS)技术广泛应用于各类分析物的检测，具有响应速度快、 检测灵敏度高、 选择性好、 易于小型化等特点[1-4]。TDLAS根据比尔朗伯定律反演气体浓度，其中气池光程是一个重要参数，它的精确度直接影响气体浓度的测量不确定度，实现测量结果直接溯源的条件之一是可溯源的气池光程，因此，对气池光程的可溯源测量有利于开发可直接溯源的气体分析仪。一般情况下，单通气池的光程可使用机械测量方法实现可溯源测量，然而，机械测量无法排除激光在气池内传播方向变化的影响，很难精确测量多通气池(如White气池、 Herriott气池)的光程，常用的方法是通过测量标准气体的吸收光谱计算气池光程。

2017年，周鑫等[5]使用DAS测量了氧气的吸收光谱，得到的单通气池光程相对机械测量结果偏差为0.78%。然而，上述测量未对结果的可溯源性进行分析，目前关于气池光程的可溯源测量研究较少报道。Nwaboh等[6]在含有White气池的光路中加入校准的单通气池，交替往其中一个气池通入标准气体并排空另一个气池，获得两种情况的吸收光谱，经比较计算得到White气池的光程，分析测量过程中引起不确定性的可能因素，最终得到的光程相对不确定度为0.20%。该方法通过校准的单通气池计算多通气池的可溯源光程，计算过程中无需知道标准气体的线强。然而，该方法与使用DAS测量气池光程相比，操作步骤相对复杂；后者虽然操作更为简单，但受限于HITRAN数据库[7]中气体吸收线强较大的不确定度，光程测量结果的不确定度相对较大。

本文以三次反射型气池的光程可溯源测量为例，使用TDLAS技术结合计量学溯源方法测量标准高纯CO2的吸收光谱，采用美国国家标准技术局最新测量得到的30012-00001跃迁带P 4e支线强(相对不确定度为0.15%)[8]反演气池光程，使用速度依赖的Voigt线型精确计算得到不同气压下的积分吸光度信号，对其进行线性回归分析，全面分析各参量的测量不确定度及其传递过程，计算得到可直接溯源的气池光程为(81.61±0.42) cm，相对标准不确定度为0.51%，测量不确定度小于直接测量结果。

1 原 理

TDLAS基于比尔朗伯定律，它描述激光透过气体的光强It(ν)与入射光强I0(ν)的关系如式(1)[9]

It(ν)=I0(ν)exp(-STrisoφ(ν-νc)nL)

(1)

式(1)中，riso是气体的同位素丰度[10]与HITRAN数据库中的同位素丰度之比(如riso=x12CO2/x12CO2HITRAN，其中x12CO2和x12CO2HITRAN分别为12CO2在取样气体和HITRAN中的丰度)，φ(ν-νc)是在中心波数νc处的归一化谱线形状，L是吸收光程，n是气体的分子数密度，ST是跃迁谱线在温度为T时的线强，其线强与温度的函数关系如式(2)[9]

(2)

式(2)中，c，h，kB和νc分别是光速、 普朗克常数、 玻尔兹曼常数和中心波数，E″表示跃迁吸收谱线的基态能级值，Q(T0)和Q(T)分别是参考温度T0和实际温度T的配分函数值，ST0是参考线强(T0=296 K)，KT表示线强的温度依赖系数。

根据理想气体状态方程p=nkBT，吸收气体分子数密度n可用该气体的压强p与气体温度T、 玻尔兹曼常数kB表示，式(1)可改写为光程L的计算式

(3)

式(3)中，α(ν)=ln(I0(ν)/It(ν))是光谱吸光度，A是积分吸光度，pχCO2是CO2的分压。通过测量特定温度T和压强p下吸收气体的积分吸光度A可得到气池光程L。

计量学溯源是指通过记录的不间断校准链将测量结果与规定的参考标准关联起来，每条校准链均影响测量不确定度[11]。一个可溯源的测量结果由均值和相应的不确定度组成，按照国际标准组织发布的指南中不确定度的计算方法[12]，若某一被测变量y是由n个彼此独立的输入参量xi(i=1, 2, …,n)根据函数y=f(x1,x2, …,xn)计算得到，那么y的合成标准不确定度uC(y)计算公式如式(4)

(4)

式(4)中，u(xi)是输入参量xi(i=1, 2, …,n)的标准不确定度，由此可得式(3)左边光程L的相对标准不确定度计算公式为

(5)

式(5)中，uL,uT,uA,uST0,uKT,up,uriso分别表示L，T，A，ST0，KT，p和riso的不确定度。只有上述输入参量可溯源，根据式(3)计算得到的光程L才是可溯源的，因此，使用校准的工具和标准的计算方法测量和计算上述输入参量，能够获得可溯源的气池光程。

2 实验部分

采用DAS技术对高纯CO2(99.999%)进行光谱测量，实验装置如图1所示。实验所用光源为FITEL公司生产的中心波长1 576 nm的DFB半导体激光器，工作温度范围和最大工作电流分别为20～35 ℃和120 mA，线宽小于2 MHz。使用武汉东隆科技有限公司的电流控制模块LDC-0050和温度控制模块LDT-0200实现对激光器的电流和温度调节，将信号发生器(RIGOLDG5102)产生的锯齿波扫描信号

DFB: distributed feedback; D: detector (InGaAs); VG: Vacuum gauge; BV: Ball valve; NV: Needle valve; GC: Gas cylinder

(重频1 kHz、 占空比9∶1)加载到电流控制模块上，以调谐激光器输出波长。

三次反射型气池为铝合金材质，其光路结构如图1中三维模型所示，激光通过单模光纤和准直透镜从气池上方耦合进气体池，从反射镜到右侧凹面镜，再次经过反射镜从气池上方耦合镜输出，激光在气池内经过了3次反射，可认为该气池是多次反射长光程气池的简化模型。直接测量光程Lm=(81.21±0.80) cm是使用校准的米尺测量三个反射点之间及其与激光耦合出入点之间的距离得到的，相对标准不确定度为0.99%，测量不确定度是综合考虑测量定位误差、 测量示值误差和测量路径与实际光路可能不重合造成的误差估算得到的。采用加热温控系统(含PT100温度传感器)使气池温度保持在(294.2±0.1) K。气池一端通过针阀与装有高纯CO2的钢瓶减压阀连接，另一端通过球阀与旋片式真空泵连接，电容薄膜规真空计(ANELVAM-342DG-13)通过三通接头与气池出气口连接，用于气池内压强的测量，使用Swagelok检漏液对气路进行气密性检测，未出现漏气现象。出射光由InGaAs探测器接收，探测器紧挨输出窗口镜，以尽可能排除空气中CO2对测量结果的影响。用示波器(KEYSIGHT DSOX3054T)同时采集经过放大的探测器信号和LDC-0050的扫描电流信号，以实现采样点与波数的转换。

使用波长计(Bristol 621B)测量了不同工作温度和电流下的激光器输出中心波数，结果如图2所示，DFB输出中心波数随工作温度的升高而减小，随电流的增大非线性减小。由于实验要测量CO2在6 344.68 cm-1附近的吸收谱线，通过观察吸收峰在电流扫描范围内的位置，设定DFB的工作温度为31.3 ℃，电流扫描范围0～90 mA，在此工作条件下，同时用波长计和示波器分别对DFB输出波数ν和扫描电流i进行采样，并对数据(νvsi)进行二次非线性拟合，得到的DFB输出波数与电流的关系模型为

ν=b0+b1i+b2i2

(6)

式(6)中，b0=(6 345.348 81±0.000 67)，b1=(-0.006 6±2.397 8)×10-5，b2=-6.255 2×10-5±2.014 7×10-7。

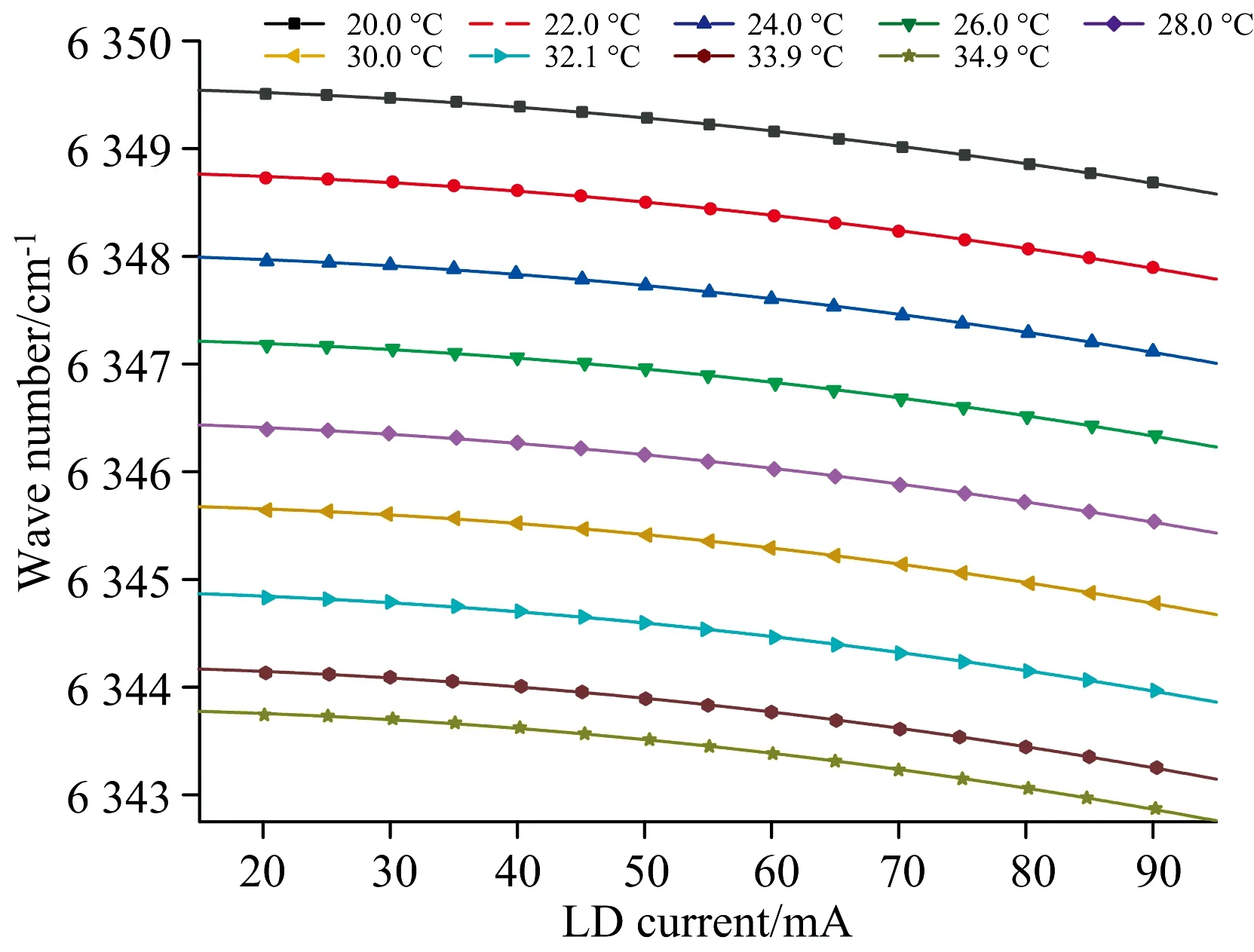
图2 DFB输出波数与温度、 电流的关系Fig.2 Output wavenumber of DFB as a functionof temperature and current

实验之前使用真空泵将气池内压强抽至0.1 Torr以下，静置310 min，气压升高0.6 Torr，估算气池系统的平均泄漏速率小于0.002 Torr·min-1。向气池内充入标准高纯CO2(99.999%)，而后抽真空，排除管道内和气池内残留的空气，重复该操作三次。缓慢通入高纯CO2至压强为100 Torr，用真空泵降低压强，待气压稳定后，分别记录压强p在74.2，59.4，48.7和36.0 Torr时的探测器信号，为提升信噪比，探测器信号经过1 000次平均，对应的采样时间为1 s，图3是p=74.2 Torr时的探测器信号和采样点对应的波数。对未吸收区域进行三次多项式拟合，获得入射光对应的基线信号。

图3 压强为74.2 Torr时的探测器信号及其 基线拟合与采样点对应的波数

根据比尔朗伯定律提取吸光度信号，将同步采集的扫描电流值代入式(6)实现采样点与波数的转换，并利用相邻两个吸收峰中心波数在HITRAN中的间隔进行校准，获得光谱吸光度信号，如图4 (a)所示(p=74.2 Torr)，其中吸收峰1的中心波数在6 344.68 cm-1附近，为本实验测量的吸收线，与其相邻的吸收峰2的中心波数在6 344.77 cm-1附近。在OriginLab软件中使用Voigt线型(VP)对不同压强下的吸光度信号进行多线拟合，拟合残差的标准差σ=5.786 44×10-4，如图4(b)所示，从残差形状可知，VP在吸收线峰值附近拟合效果较差(局部标准差σlocal=7.895 89×10-4)。进一步使用二次速度依赖Voigt线型(qSDVP)[13]进行多线拟合，拟合残差的标准差σ=3.565 12×10-4，如图4 (c)所示，在吸收线峰值附近的残差标准差σlocal=2.826 4×10-4，在整个拟合范围内的残差形状较为平坦，拟合效果较好。使用qSDVP拟合不同气压下的光谱吸光度，得到对应的积分吸光度及其相对标准不确定度(relative standard uncertainty, RSU)如表1所示。

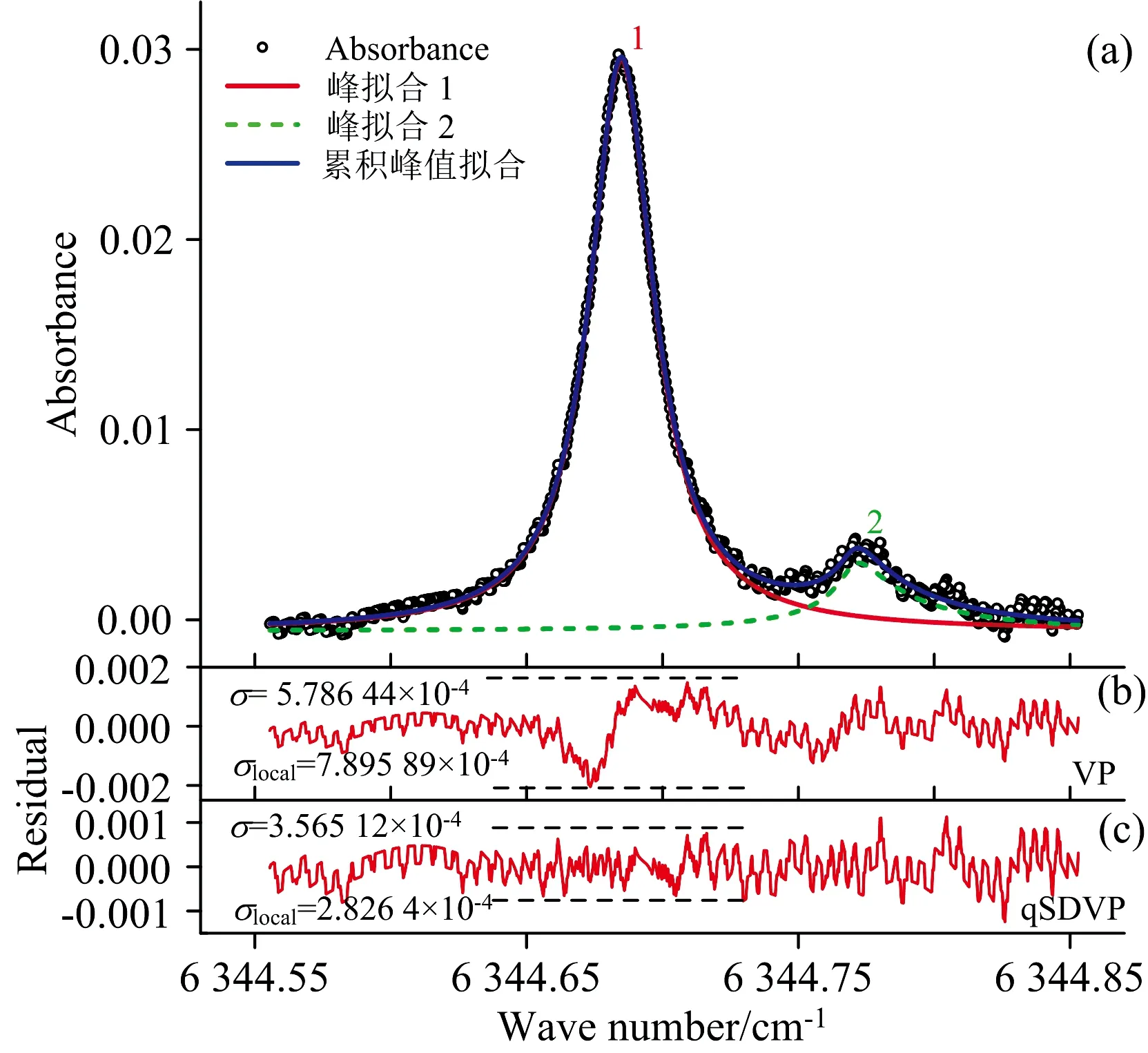
图4 压强为74.2 Torr时的(a)光谱吸光度及qSDVP拟合，(b) VP拟合残差，(c) qSDVP拟合残差

表1 不同压强下的积分吸光度及其相对标准不确定度Table 1 Integral absorbance and corresponding RSUat various pressure

3 结果与讨论

要实现气池光程的可溯源测量，需对等式(3)右边的各个测量变量进行溯源分析，确定各个变量的相对标准不确定度(RSU)。玻尔兹曼常数kB为标准值，不确定度为0。温度和压强是经校准的传感器测量得到的，测量结果可直接溯源至国际标准(SI)。气体温度T=294.2 K是使用PT 100传感器测量得到的，该传感器测量的标准不确定度为0.2K，RSU为0.07%，其他因素如温度分布的不均匀性对最终测量量值的不确定度贡献很小，本文不作考虑。

实验使用的电容式真空计测量精度为0.2%，泄露在数据采集时间内(1 s)引起压强变化小于3.3×10-5Torr (0.004 4 Pa)，在最小实验压强p=36 Torr (4.8×103Pa)时引起的RSU小于0.0001%，可忽略不计。虽然真空泵无法抽至绝对真空，但反复用高纯CO2清洗气池后，可忽略残留空气对CO2压强测量的影响，因此气体压强p的RSU为0.2%。同位素丰度比riso=1.000参考文献[10]，响应的RSU为0.05%。实验使用的气体为标准高纯CO2(99.999%)，气体浓度值取χCO2=1，RSU为0.001%。

最关键的参数线强S1, T0=(6.647±0.010)×10-24cm·molecule-1(RSU为0.15%)取自美国国家标准技术局最新测量得到的30012-00001跃迁带P 4e支参考温度下的线强[8]，该线强量值与对应的RSU已被纳入HITRAN数据库[14]，将作为HITRAN 2020版本中CO2光谱参数的更新内容之一。根据HITRAN中的光谱数据，图4(a)中的吸收线1的展宽范围内包含40012-10001跃迁带P 2e支谱线，该线强S2, T0=9.768×10-27cm·molecule-1(RSU为2%)。其他几支线强量级小于10-28cm·molecule-1在本实验压强条件下吸收强度很小，不作考虑。根据Nwaboh等关于线强的不确定分析[15]，式(2)右边的输入参量Q(T0)，Q(T)，h和νc对ST的不确定贡献几乎为零，当气体温度T的不确定度为0.2 K时，KT的相对标准不确定度约为0.053%。将T=294.2 K和HITRAN数据库中上述P 4e与P 2e两支谱线对应的光谱参数值代入式(2)分别得到K1, T=1.014 6，K2, T=0.973 6。综上分析，式(3)中ST0KT=S1, T0K1, T+S2, T0K2, T。

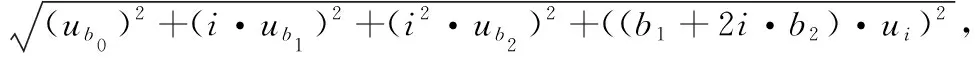
为了计算不同压强下光程L的均值及其标准不确定度，将式(3)改写为如式(7)形式

(7)

式(7)中，Γ的取值对应不同的压强p。使用在线工具[16]对不同压强下的Γ值及其标准不确定度进行估算，获得横纵坐标均具有标准不确定度(AvsΓ)数据，对该数据进行线性回归分析，结果如图5所示，图中蓝色和绿色误差棒分别表示Γ和A的标准不确定度。由线型回归模型的斜率可得最终计算的气池光程L=81.61 cm，标准不确定度为uL=0.42 cm，相对标准不确定度为0.51%。由于截距值小于其不确定度值，回归模型的截距参数值没有意义，表明测量的气池光程是可靠的。与直接测量光程(81.21±0.80) cm相比，本实验测量的可直接溯源至SI的光程相对偏差为0.49%，不确定度更小。

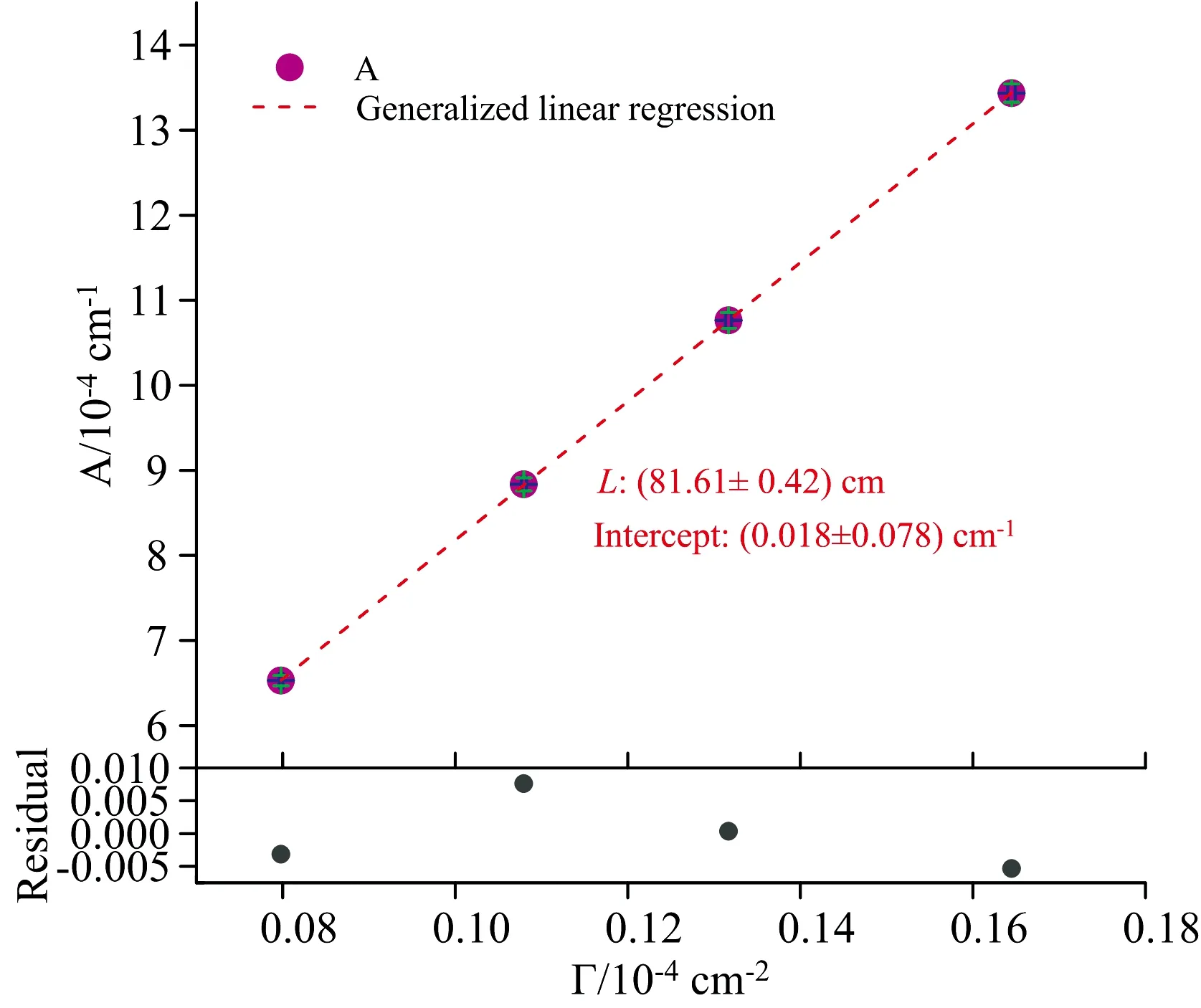
图5 积分吸光度A与Γ的关系及其线性回归分析Fig.5 Integral absorbance A as a function ofΓ and its general linear regression

表2展示了光程L的不确定度估算和各输入参量对不确定度的贡献。由表可知，主要影响光程不确定度的因素是拟合的积分吸光度Afit和波数ν的不确定度，其贡献占比分别为29.10%和43.98%。影响Afit不确定度的主要因素是光谱吸光度的信噪比，CO2在6 344.68 cm-1附近吸收强度相对较弱，实验中的气池光程限制了信噪比的提升。然而，当测量多通长光程气池的光程时，信噪比能得到较大提升，进而能够降低Afit的贡献占比。波数ν的不确定度主要来源于扫描电流的稳定性，可通过提升扫描电流稳定性来降低其贡献占比。采用的线强S1, T0不确定度(0.15%)较小，对于减小光程的测量不确定度具有重要作用。虽然线强S2, T0的不确定度(2%)较大，但由于其量值比S1, T0小3个数量级，因此其对最终结果的不确定度贡献几乎为零。

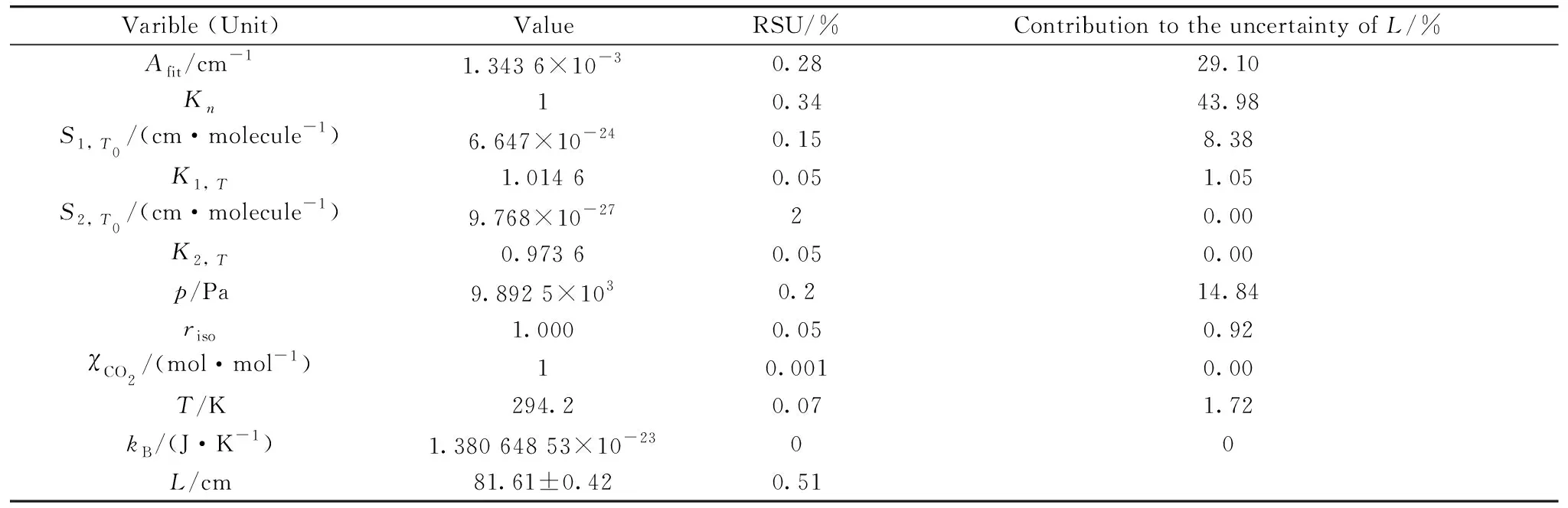
表2 光程L的不确定度估算Table 2 Uncertainty budgets for optical path length L

4 结 论

基于TDLAS技术，搭建了气池光程可溯源测量实验系统，采用美国国家标准技术局最新测量得到的CO2气体30012-00001跃迁带P 4e支线强(不确定度为0.15%)，对具有多次反射光路结构的单次反射型气池光程进行了可溯源测量。全面分析了各输入参量的不确定度及其传递过程，最终获得可直接溯源的气池光程L=(81.61±0.42) cm，相对标准不确定度为0.51%，与直接测量量值相对偏差为0.49%。对光程不确定度贡献最大的是拟合的积分吸光度和波数的不确定度，改善二者的不确定度是进一步提升光程测量精度的关键。增大光程可以提升吸收光谱信噪比，有利于改善积分吸光度的拟合不确定度，进而提升光程测量精度，因此本系统亦适用于多通长光程气池的光程可溯源测量。