浅谈含容电路回路电阻理想化处理的正确性
孙朝晖
(宁波市北仑中学 浙江 宁波 315800)
图1所示的含容电路中质量为m的导体棒垂直于无限长直导轨放置且接触良好;电容器为C,初时刻不带电;忽略回路电感;导轨宽为L.规定矢量向右为正,电容器下极板电势为零,回路电流逆时针流向为正,磁感应强度B如图所示.
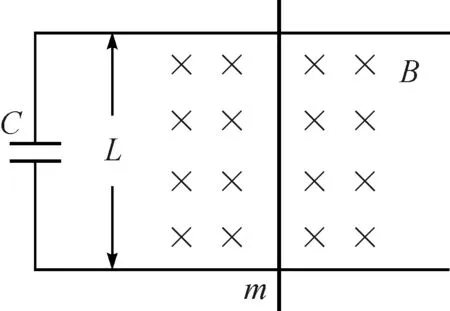
图1 导体棒在含容电路中切割磁感线示意图
下文将在导体棒处于不同初始条件下,分别对回路各部分的状态量、过程量等进行定量计算并分析讨论,从而分析两种初始条件下回路电阻理想化处理的正确性.
1 导体棒以初速度v0向右切割磁感线
如图2所示,导体棒从初速度v0减速至最终速度v1,后以无限趋近v1的速度做匀速运动,稳态时导体棒动生电动势与电容器电势差相等,回路电流为零.
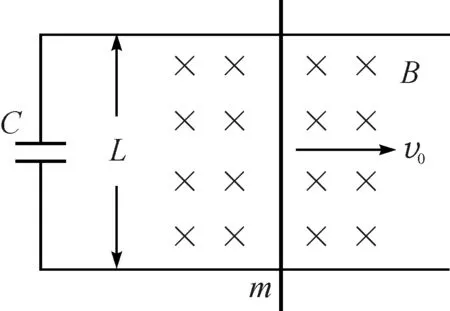
图2 导体棒在含容电路中以初速度v0切割磁感线示意图
1.1 理想化处理:忽略回路电阻
因忽略电阻,故回路未产生焦耳热.该系统导体棒在向右做减速运动过程中,动能减小部分完全转化为电容器的电场能.可得
E1=BLv1
(1)
Q1=CE1
(2)
(3)
(4)
由
ΔEk=WC
再结合式(1)解得最终速度为
(5)
注:如此分析存在问题,后文会进行讨论.
1.2 不忽略回路电阻R
回路电阻为R,则该系统导体棒动能的减小部分转化为电容器的电场能和回路电阻的焦耳热.对导体棒用动量定理,有
dp=Fdt=-BILdt=-BLdq
即为
mv1-mv0=-B2L2Cv1
(6)
从而解得
(7)
分别单独计算导体棒从初态到稳态的过程中动能减小量ΔEk、电场能增量WC以及电阻的焦耳热Q
(8)
(9)
考虑导体棒切割磁感线过程中的一般情况,由基尔霍夫电压定律得
该式两边对时间求导得
由以上微分方程解得回路电流的表达式为
(10)
通过积分求得电阻在t0时间内的焦耳热为
(11)
导体棒达到最终速度的过程中,总焦耳热为
(12)
1.3 讨论
1.2中的式(8)、(9)、(12) 经验证,ΔEk=WC+Q恒成立,符合能量守恒定律,回路存在焦耳热但无额外电磁辐射能量损耗.
发现电阻最终焦耳热Q(∞)表达式与电阻R无关,不能因为R很小就将之忽略,否则能量就不守恒了.而式(5)与式(7)的差异就在于,前者对回路电阻理想化处理.在1.1中若忽略回路电阻,则动生电动势时刻等于电容器电压,电容器时刻处于满充状态,于是回路也就没有电流了,明显与初状态矛盾.故回路电阻不能理想化忽略,式(5)计算错误,式(7)计算正确.
实际上,回路电阻越小,则回路RC常数越小,回路充电就越快,但由于充电电流较大,由式(11)可知距初态相同时间t0内的焦耳热会越大.由式(12)可知,从初态到稳态的全过程中,由于达到稳态所需时间无穷大,在考虑总焦耳热时不能因电阻很小而作理想化处理将之忽略.但在有限时间t0内,由式(11)可知,R越小,Q越小,当R→0时,焦耳热Q(t0)→0,此时将回路电阻作理想化处理是正确的.
2 静止导体棒受恒力F向右加速
如图3所示,导体棒从静止开始受恒力F与安培力的合力,向右做加速运动.

图3 导体棒在含容电路中受恒力F由静止开始切割磁感线示意图
2.1 忽略回路电阻
(13)
F-BIL=ma
(14)
以上两式解得导体棒加速度和回路电流为
(15)
(16)
由式(15)可知导体棒做匀加速直线运动.恒力F在有限时间t0内做功WF,该功转化为电容电场能WC及导体棒动能Ek.可计算得
(17)
(18)
(19)
经验证,确实WF=WC+Ek符合能量守恒定律,因忽略电阻,故回路无焦耳热.
2.2 考虑回路电阻R
动生电动势等于电容器与电阻上的压降之和
该式两边对时间求导有
又

(20)
解得导体棒加速度及回路电流的表达式为
(21)
(22)
进一步通过积分求得电阻的焦耳热为
故对于电阻焦耳热的计算
(23)
2.3 讨论
在有限的时间t0内,由式(23)可知当R→0时,焦耳热Q→0,此时将电阻理想化处理而忽略焦耳热是正确的.但在无限长时间内,电阻焦耳热为无穷大.
3 结论
结合上文的分析,将电磁感应中含容电路在两种初始条件下运动情况及回路电阻理想化处理的正确性进行汇总分析,如表1所示.

表1 两种初始条件下导体棒运动情况
在导体棒以初速度v0向右切割磁感线的初始条件下,电容器初态端电压为零,而导体棒初态电动势非零,此时回路若无电阻,可得电容器端电压等于导体棒端电压,但这明显是矛盾的.因此,研究电容器的充电电流等相关问题时,不能将回路电阻理想化处理而忽略.
在理想化处理中,忽略电阻的焦耳热并不机械地等同于回路没有电阻.上述两种初始条件,在有限的时间内,当回路电阻R趋近于零的时候,回路的焦耳热也确实趋近于零,此时在研究回路的能量时将焦耳热忽略是正确的.但由于电阻的存在,电容器电压并不等于导体棒的感应电动势,电容器还时刻处于充电状态,回路电阻也因两端电势差非零而使得回路存在充电电流.虽然回路电阻很小,或回路充电电流很小,在无限长的时间里,其焦耳热的累加也并非为零.因此,在有限的时间里,若仅研究回路的焦耳热,在回路电阻很小的时候可以将之忽略.但在研究电容器的充电电流等相关问题时,不能将回路电阻理想化处理而忽略;在无限长时间里,在考虑回路焦耳热和电容器充电电流问题时,往往不能将回路电阻忽略.

