巧用教材原题及衍生题探析“法拉第圆盘”类问题

周佳

(清华附中嘉兴实验高中 浙江 嘉兴 314000)

1 引言

高中物理人教版上放置了两道“法拉第圆盘”类问题．一道在新、旧教材的“涡流、电磁阻尼和电磁驱动”一节中，另一道先在旧教材“楞次定律”一节中[1]，后在新教材中转移到“电磁感应”一章的“复习与提高”板块[2]并增加了一个小题．这两道教材原题与之后在各类考试中出现的衍生题均引起了师生的广泛讨论，笔者将这类问题梳理、对比，纠正部分学生的错误观念，总结出切实可行的解题思路与方法．

2 教材原题及解析

【教材题1】有一个铜盘，轻轻拨动它，能长时间地绕轴自由转动．如果在转动时把蹄形磁铁的两极放在铜盘的边缘，但并不与铜盘接触(图1)，铜盘就能在较短的时间内停止．分析这个现象产生的原因．

图1 题图

解析:铜盘可视为由无数根导线并列组成，形成无数个闭合回路．在磁场中转动时每根“导线”都会切割磁感线从而产生感应电流，宏观上形成涡流．由楞次定律可知，“通电导线”受到的安培力与其相对运动的反向相反，故铜盘能在较短的时间内停止．

疑难梳理:部分学生存在疑惑，在铜盘转动过程中，其面积没有变化，则通过铜盘的磁通量也不变，根据电磁感应定律，不会有感应电流产生，怎么会有安培力呢？这是典型的 “通量法则佯谬”，回顾法拉第电磁感应定律的完整表述——闭合电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比．须注意到磁通量变化必须针对某一闭合回路来讲，学生的误区在于认为整个圆盘只有一个大回路(图2)．事实上虽然整个圆盘的磁通量不变，但圆盘上可以划取无数回路，其中任何一个回路都在随着圆盘转动[3]，如图3所示，回路a、b在进出磁场的过程中都会发生磁通量的变化，从而产生感应电流，宏观上形成涡流．

图2 学生认为的闭合回路

图3 铜盘中的无数回路

【教材题2】图4是法拉第发明的圆盘发电机示意图，铜盘安装在水平的铜轴上，它的边缘正好在两磁极之间，两块铜片C、D分别与转动轴和铜盘的边缘接触．使铜盘转动，电阻R中就有电流通过．

图4 法拉第圆盘发电机示意图

(1)说明圆盘发电机的原理．

(2)圆盘如图4方向转动，请判断通过R的电流方向．

(3)如果圆盘的半径为r，匀速转动的周期为T，圆盘处在一个磁感应强度为B的匀强磁场之中．请讨论这个发电机的电动势与上述物理量的关系．

解析:(1)从“切割”的角度来看，圆盘可看成由无数根半径为r的辐条组成，圆盘转动时每根辐条都在切割磁感线产生感应电动势，相当于电源的作用；从电磁感应定律的角度来看，圆盘转动过程中闭合回路CDRC的磁通量发生变化，从而产生感应电流．

(2)由右手定则可知，感应电流方向为C至D．

(3)如图5所示，顺着磁场方向看，闭合回路CDRC在极短时间Δt内的面积变化量为扇形CDD′的面积，设圆盘半径为r，旋转角速度为ω，则

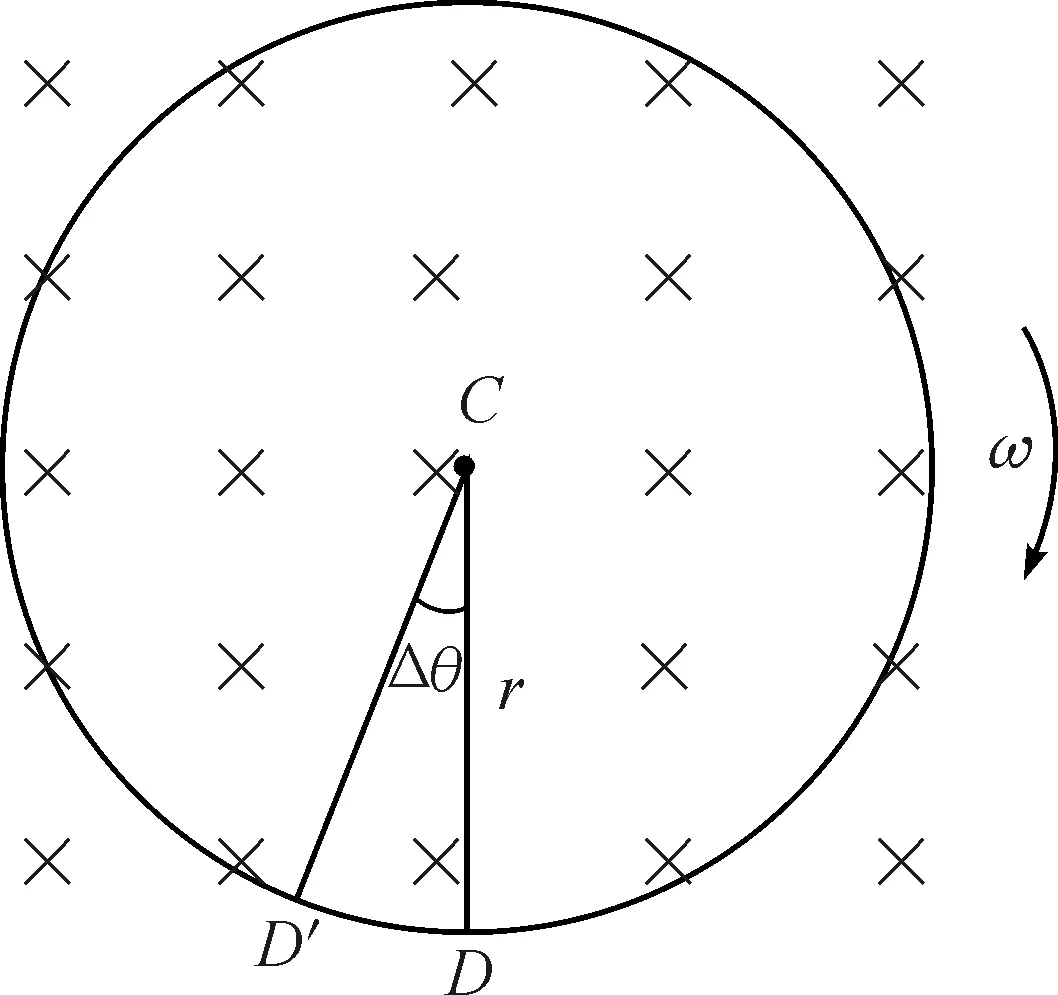
图5 回路CDRC的面积变化

由电磁感应定律可得

疑难梳理：部分学生沿用上一题的思路分析该题，认为既然磁场范围足够大，那么圆盘上任何回路的磁通量在转动过程中都不变，无法产生感应电流．该疑惑的症结在于机械照搬方法而没有抓住“闭合回路”的正确观念，此题中的闭合回路是由圆盘辐条CD与外电路构成的，即CDRC回路，而其他主观划分的回路均不与外电路连通，因此没有分析的意义．这时有学生提出，图中显示CDRC回路平面与磁场方向平行，因此磁通量始终为零．该观点的错误之处在于认为CD部分是固定不动的，但事实上CD是圆盘沿半径方向的“辐条”，随圆盘的转动而转动．还有学生从“切割”的角度加以分析，认为每根辐条在一瞬间切割之后就与外电路断开，因此不会形成稳定电流．该思路忽视了圆盘是由无数根辐条并排而成的，上一根辐条与外电路断开后的下一瞬间，下一个辐条便与外电路连通，该过程随着圆盘的转动而不断重复，因此能够形成稳定的电流．综上，该题结果与匀强磁场的范围无关．

3 教材衍生题及解析

【衍生题1】有一个铜盘，轻轻拨动它，能长时间地绕轴自由转动．若将铜盘置于足够大的匀强磁场中(图6)，铜盘能在较短的时间内停止下来吗？

图6 衍生题1题图

解析：如图7所示，由于匀强磁场足够大，所以对于铜盘上所有的回路，其磁通量在转动的时候都不变，因此不会产生感应电流，铜盘不会在较短时间内停下来．

图7 铜盘上的无数回路

疑难梳理：若将题干中的足够大的匀强磁场改为足够大的非匀强磁场呢？圆盘转到不同位置时，其回路的磁通量会发生变化，所以会产生感应电流与安培力，铜盘能够在较短时间内停下来．

【衍生题2】电阻不可忽略的导电圆盘的边缘用电阻不计的导电材料包裹，圆盘可绕固定点O在水平面内转动，其轴心O和边缘处电刷A均不会在转动时产生阻力，空气阻力也忽略不计．用导线将电动势为E的电源、导电圆盘、电阻和开关连接成闭合回路，如图8(a)所示在圆盘所在区域内充满竖直向下的匀强磁场，如图8(b)所示只在A、O之间的一块圆形区域内存在竖直向下的匀强磁场，两图中磁场的磁感应强度大小均为B，且磁场区域固定．将图8(a)和图8(b)中的开关S1和S2闭合，经足够长时间后，两图中的圆盘转速均达到稳定．则( )

图8 衍生题2题图

A.从上往下看，圆盘沿顺时针方向转动

B.刚闭合开关时，图8(a)中的圆盘比图8(b)中的圆盘加速得快

C.将两图中的开关断开，图8(b)中的圆盘仍然匀速转动

D.将两图中的开关断开，图8(a)中的圆盘比图8(b)中的圆盘减速得快

解析:图8(a)、(b)中圆盘上的电流方向均为O到A，根据左手定则可知，从上往下看圆盘沿逆时针方向转动，选项A错误．因为两图中的圆盘完全相同，因此刚闭合开关时，圆盘的加速度大小仅取决于安培力大小，需要针对安培力公式F=BIL中的3个因素加以分析．由于电路和圆盘完全相同，所以两图中从O至A的电流大小相同，此外磁感应强度B也相同，所以安培力大小只须看两图中L的大小．图8(a)中圆盘受到安培力部分的有效长度为半径OA，图8(b)中的有效长度为圆形磁场区域的半径，小于OA．综上图8(a)圆盘受到的安培力更大，所以加速得更快，选项B正确．若将开关断开，由于图8(a)中的磁场区域足够大，因此圆盘上任何回路在转动过程中的磁通量都不变，不会产生感应电流和安培力，仍然匀速转动．而图8(b)中的磁场在有限区域内，因此圆盘上所有回路在进出磁场时都会引起磁通量的变化，从而产生感应电流和安培力，将减速转动，选项C、D错误．故选项B正确．

疑难梳理:开关闭合时的物理本质为通电导线所受的安培力，两图区别为“导线”的有效长度不同．开关断开时的物理本质为电磁感应，物理模型为孤立导体盘，图8(a)相当于衍生题1，图8(b)相当于教材原题1，分析时抓住闭合回路的磁通量这一关键点．也可以从“切割”的角度分析，开关断开后的孤立圆盘可看作由无数根沿半径方向的辐条并排而成，因为图8(a)磁场布满整个圆盘，所以这些辐条产生的感应电动势都等大，电荷只在盘心和盘边缘处积累，无法在圆盘内部形成电流，故不会产生安培力．而图8(b)中的磁场存在于部分区域内，只有一部分辐条产生感应电动势，可以在圆盘中形成电流(图9)[4]，产生安培力．

图9 辐条切割磁感线产生的电流

如何理解题干中“经足够长时间后，两图中的圆盘转速均达到稳定”？这与反电动势有关，圆盘转动时产生感应电流，进一步产生安培力，阻碍圆盘的转动，并且随着速度的增大而增大，当该反向安培力与此前的正向安培力平衡时，圆盘达到最大速度，之后速度保持不变．

图10 衍生题3

(1)线圈的EF边刚刚越过磁场边界OA时，该线圈产生的电动势的大小和受到的安培力大小F；

(2)以EF边通过磁场边界OA为计时起点，画出该线圈穿越Ⅰ、Ⅱ两磁场区域的过程中电流随时间的变化图像，以逆时针为电流正方向；

(3)从EF边通过磁场边界OA开始，转盘转一圈的过程中，94个线圈产生的总热量Q．

解析:(1)EF边切割磁感线产生感应电动势，其大小

E=nBLv

因为r比L大很多，所以

v≈ωr

可得

E=nBLωr

代入数据得

E=15 V

根据安培力公式可得

代入数据得

F=6 N

(2)EF边进入磁场Ⅰ且GH边没有进入磁场Ⅰ时，仅EF边切割磁感线，感应电流大小为

可得I=3 A，根据右手定则可知电流方向为逆时针；EF边进入磁场Ⅱ且GH边进入磁场Ⅰ时，EF和GH边均切割磁感线，根据右手定则可知，此时感应电动势的大小E′=2E=30 V,感应电流大小

即I′=6 A，方向为顺时针；EF边离开磁场Ⅱ且GH边尚在磁场Ⅱ时，仅GH边切割磁感线，此时感应电流

即I=3 A，方向为逆时针．因为转盘匀速转动，所以进、出磁场时间相同，每个阶段持续的时间均为

代入数据得

综上可画出I-t图像，如图11所示．

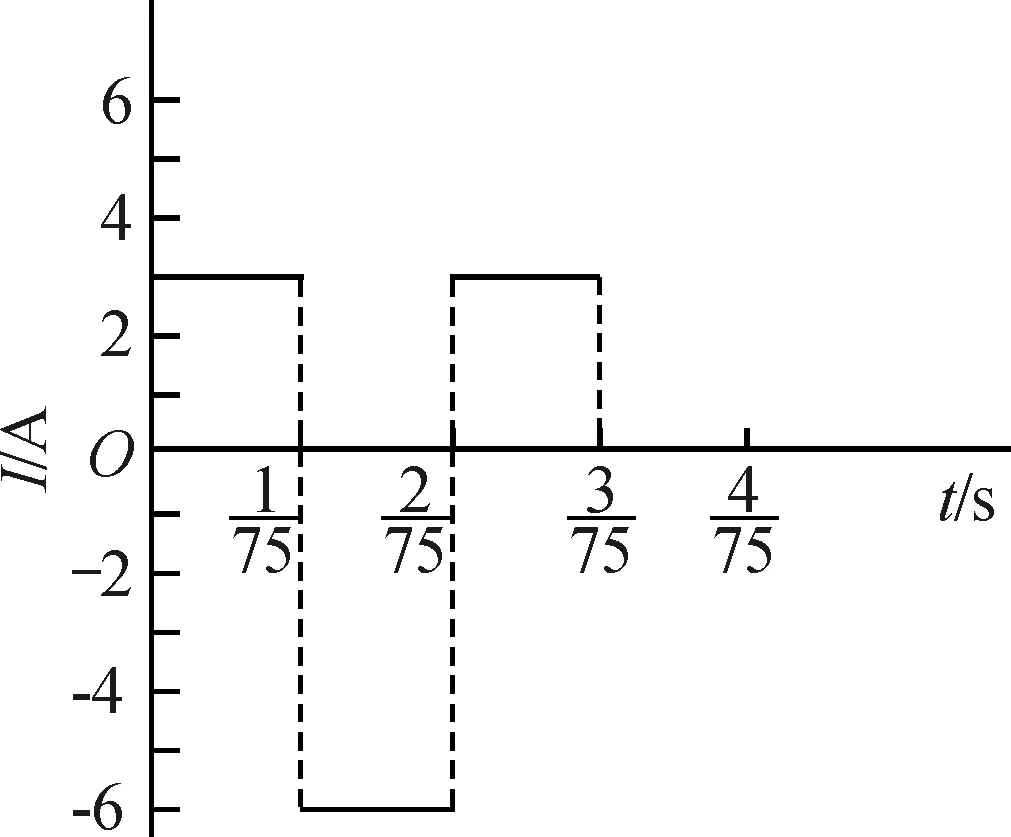
图11 电流随时间的变化图像

(3)在转盘转一圈的过程中，对任意线圈分析可得热量

Q=2I2RΔt+I′2RΔt

代入数据得

Q=3.6 J

由题意可知所有线圈都相同，且相对于转盘圆心对称分布，因此总热量

Q总=94Q=338.4 J

疑难梳理:该题不直接考查法拉第圆盘的原理，而是将原理分解转化为题干，体现在一处简化与四处理想化处理．解题时须关注四个理想化处理的目的，处理(1)说明可以用BLv计算感应电动势；处理(2)为了简化第二小题感应电流的计算；处理(3)说明每个线圈都挨个连续进入磁场，中间没有空档期；处理(4)说明了线圈在同一切割阶段内产生感应电流大小不变．此题难在审题，易在计算，若事先掌握了教材原题1的物理模型，则不会对看似复杂的题干产生陌生感和恐惧感，能够迅速完成解题．

4 总结

通过以上教材原题与衍生题的分析，我们发现解决法拉第圆盘类问题的关键在于确定闭合回路．外接无源回路时，分析对象是由圆盘辐条与外电路所组成的闭合回路；无外接回路时，分析的对象是圆盘内部的无数个任意回路．外接有源回路时，圆盘运动过程中产生反电动势，也会形成感应电流．由此可以总结出在不同外接回路及所处磁场的情况下，法拉第圆盘类题目的物理特征，如表1所示．若将“部分匀强磁场”与圆盘所处的无磁场区域看作一个整体，该整体相当于一个“全域非匀强磁场”，因此表1中第四、五行的结果是相同的，本文不作具体论述．

表1 不同条件下“法拉第圆盘”类问题的物理特征