数控机床机电-刚柔耦合特性分析下的进给系统动态运动误差溯源方法

卢成伟,吴铖洋,钱博增,向皖生,项四通*,,3

(1.宁波大学 机械工程与力学学院,浙江宁波 315211; 2.宁波精雕数控工程有限公司,浙江宁波 315211;3.上海交通大学 机械系统与振动国家重点实验室,上海 200240)

数控机床作为制造业的“工作母机”,能加工各种复杂表面,生产效率高、灵活性好且装夹时间短,在提升国家制造业水平上起着举足轻重的作用[1]。如图1所示,运动误差是影响机床加工精度的重要因素,包括静态运动误差与动态运动误差。“静态运动误差”的定义为[2]:由于制造与装配误差引起的运动轴几何精度丢失,包括几何误差与热误差,具有非时变性;“动态运动误差”的定义为[3]:由于机床进给率、速度或加速度变化,形成切削力引起的结构变形及振动,具有时变性与动态性。

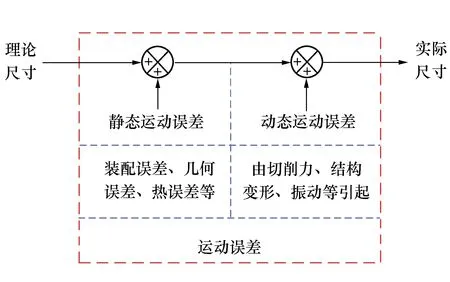
图1 影响机床加工精度的动静态运动误差

关于机床进给系统的静态运动误差辨识、建模与补偿已经相对成熟[4-6],但是关于动态运动误差规律和典型特征尚不明确,严重阻碍了数控机床加工精度提升。然而,随着制造业对机床精度的要求越来越高,动态运动误差的机理溯源对制造出高质量、高精度的数控机床显得尤为重要。

机床进给系统的动态运动误差是伺服系统和机械结构两者耦合作用的结果[7]。目前,国内外研究人员对机床动态运动误差的影响因素、误差模型、产生过程等[8-9]开展了相应的研究。影响因素方面:Andolfatto等[10]系统地划分了影响工件加工精度的主要因素,同时利用3个电容式位移传感器研究动态运动误差的影响因素,结果表明,速度和加速度越大,机床的动态运动误差越大。Li等[11]在试验模态试验和工作模态试验的基础上,对机床进行了不同进给速度下的模态试验,研究发现,五轴数控机床的阻尼和频率随机床进给速度的变化而变化。误差模型方面:Altintas等[12]和Brecher等[13]指出机床误差模型是追溯动态特性的关键,并基于数控编程路径与控制系统仿真实现了机床加工性能的联合仿真。Zhang等[14]采用有限元方法,综合考虑机床的集中质量单元、分布质量和轴间耦合等因素,构建了机床的动力学模型,并预测了机床的动态精度。产生过程方面:王磊等[15]根据进给系统刚柔特性,研究速度、加速度、刚度、阻尼等因素对动态运动误差的影响。李杰等[16]考虑机床进给系统的集中柔性和分布柔性,建立了进给系统的动力学模型,并以此为基础,通过MATLAB/Simulink仿真分析了输入信号为阶跃或正弦信号时,线性进给系统动态误差的产生过程。

上述学者的研究在动态运动误差领域已取得了一定的成果,但主要集中于对动态运动误差的理论分析,基于实际切削试件溯源动态运动误差的研究相对较少。本文以一台三轴数控立式加工中心为研究对象,以实际切削试件为本源,提出了基于机电刚柔耦合特性分析的动态运动误差溯源方法。具体为:将实际切削圆试件的三坐标标定结果与机床空载下的球杆仪圆测试结果对比,同时,考虑伺服三环控制回路和机械结构的刚柔特性,建立了机电刚柔耦合动力学模型。通过比较实际切削与模型仿真的结果,溯源由伺服系统和机械结构产生的动态运动误差。

1 动静态运动误差分离原理

机床动静态运动误差综合作用导致圆试件尺寸存在偏差,其总误差E由静态运动误差Estatic与动态运动误差Edynamic构成,即

E=Edynamic+Estatic

(1)

其中,动态运动误差Edynamic主要是由伺服系统Eservo和机械结构Emecha两方面引起,即

Edynamic=Eservo+Emecha

(2)

机床动静态运动误差的分离原理如图2所示。不同进给速度下切削圆试件后,使用三坐标测量机标定其实际尺寸,并减去其理论尺寸即为该圆试件的总误差E。在机床空载状态下进行球杆仪圆测试,因不存在切削力,故可忽略由机械结构引起的动态运动误差(Emecha),因此球杆仪测试结果可视为静态运动误差(Estatic)与伺服系统引起的动态运动误差(Eservo)之和,即为(Estatic+Eservo)。总误差E减去球杆仪测试结果,即可分离出由机械结构引起的动态运动误差(Emecha),即

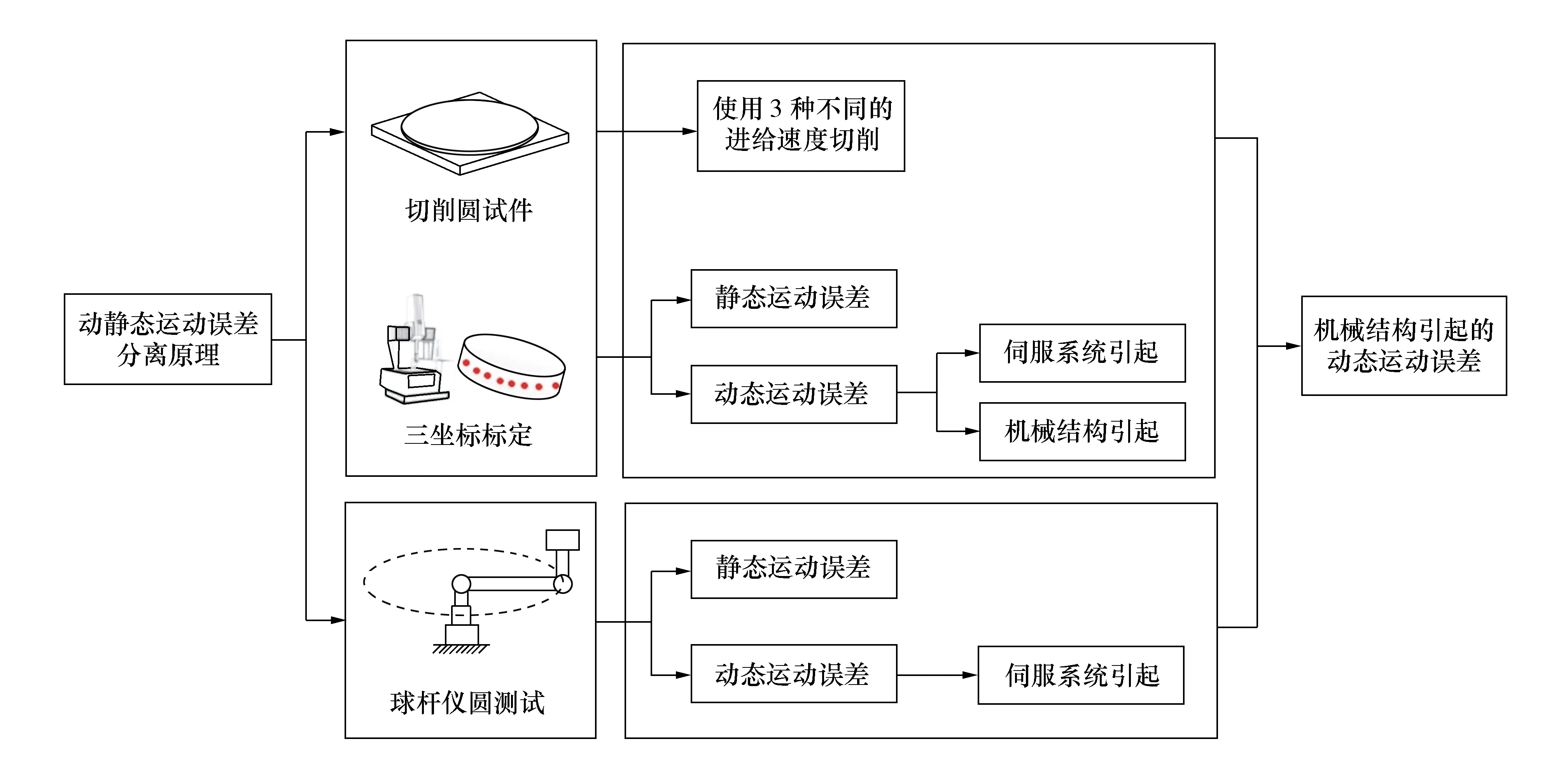
图2 动静态运动误差分离原理

Emecha=E-(Estatic+Eservo)

(3)

2 机电刚柔耦合动力学建模

2.1 直线进给系统物理模型

如图3所示,数控机床直线进给系统主要由伺服电机、联轴器、滚珠丝杠副、直线导轨、滑块、工作台、前后支撑轴承等组成。本实验中,该机床的滚珠丝杠左端前支撑轴承采用固定的安装方式,右端后支撑轴承采用游动的安装方式。

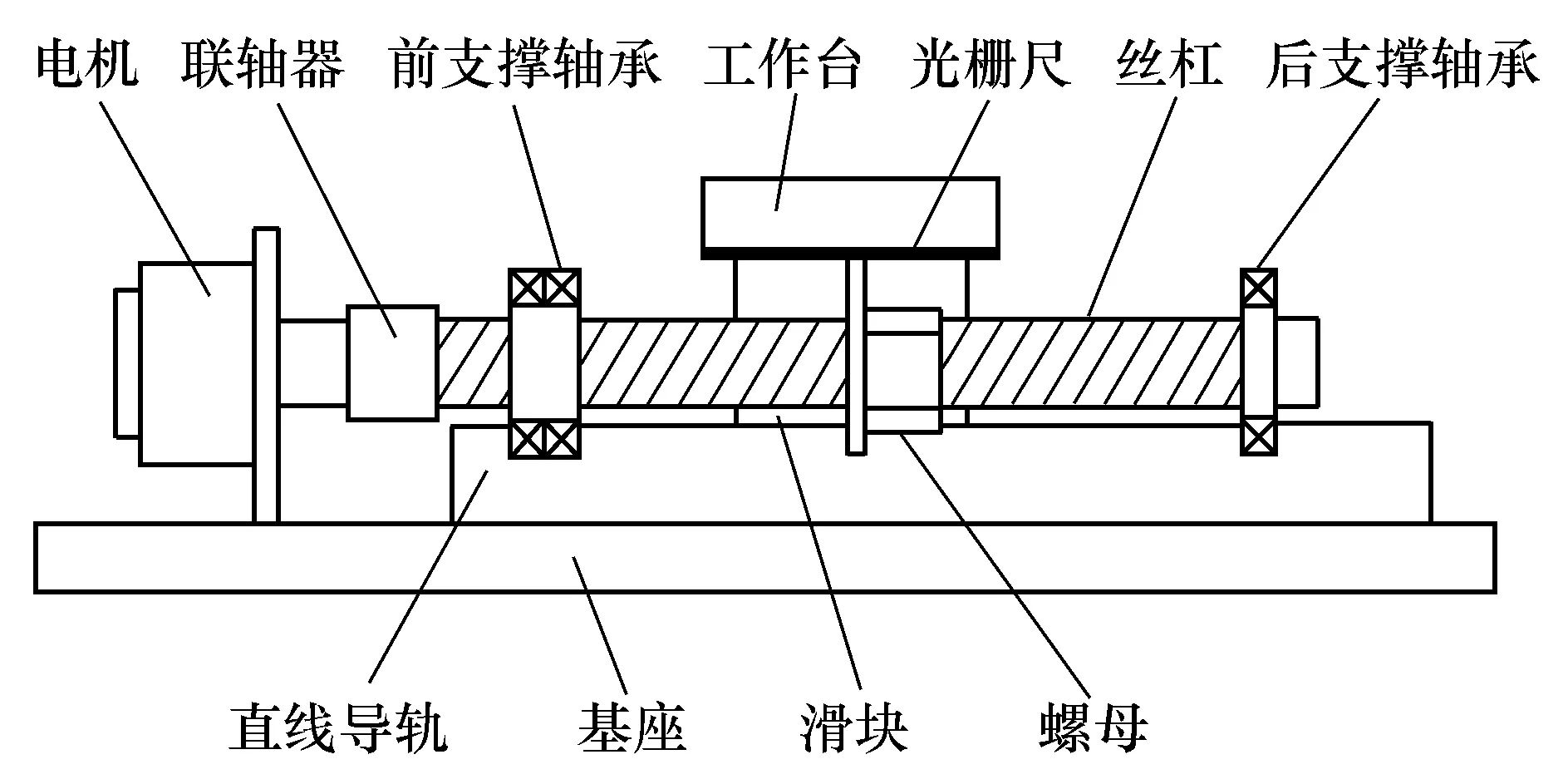
图3 直线进给系统的物理结构

2.2 机电刚柔耦合建模

直线进给系统中电机的回路电压U(t)可根据基尔霍夫电压定律求得,反电动势Ec(t)可根据电磁感应定律求得,即

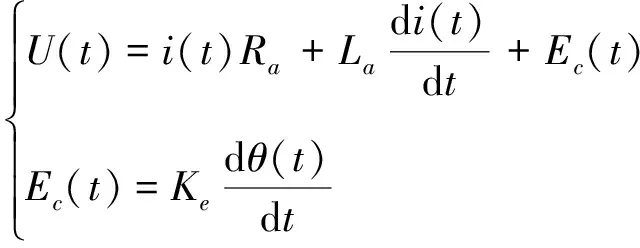
(4)

式中:i(t)为回路电流;Ra,La,Ke分别为电机的电枢电阻、电感和反电动势系数。

电机在驱动电流下产生的转矩Tm(t)为

Tm(t)=Kti(t)

(5)

式中Kt为电机的扭转常数。

联轴器和丝杠螺母是关键的动力传递和转换部件,其结构和性能参数对直线进给系统的动态精度有一定的影响。因其在机床实际切削加工中会产生微小变形,所以不能将它们完全按照刚体进行分析,故建立如图4所示的进给系统动力学模型。

图4 直线进给系统动力学模型

图4中:Jm和Js分别为电机和滚珠丝杠的等效转动惯量;Tm和θm分别为电机的输出转矩和输出角位移;k1为联轴器的扭转刚度;k2为丝杠与螺母之间的连接刚度;θs为滚珠丝杠转动的角度，可按导程P折算出位移xs;mt为工作台的质量,其直线位移为xt;Bs为滚珠丝杠两端轴承引入的黏性阻尼；Bt为工作台的滑动阻尼。上述机械结构参数的具体数值见表1所示。

表1 直线进给系统的机械结构参数

在不考虑电机内部机械阻尼的情况下,电机的输出力矩Tm(t)可表达为

(6)

式中:T1(t)为电机的负载力矩;i为电机的减速比。

根据图4建立的动力学模型,可得该进给系统的动力学方程为:

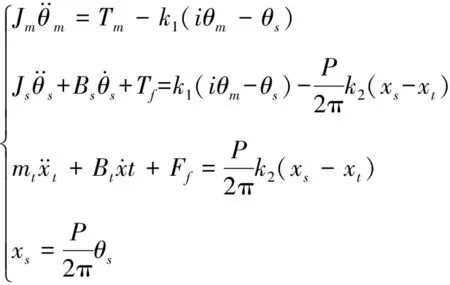
(7)

传统的动力学模型一般未考虑机械结构间的摩擦力,但实际切削中由于摩擦力对机床的动态运动误差分析存在一定影响,因此本文动力学模型综合考虑了丝杠螺母间以及导轨与滑块间的摩擦力的影响。

丝杠螺母间的等效摩擦力矩Tf可视为库仑摩擦力矩[17],表示为

Tf=Tcsgn(v)

(8)

式中:Tc为库仑摩擦力矩;v为相对滑动速度。

导轨与滑块间的摩擦力可用Stribeck摩擦力模型来表示[17],即

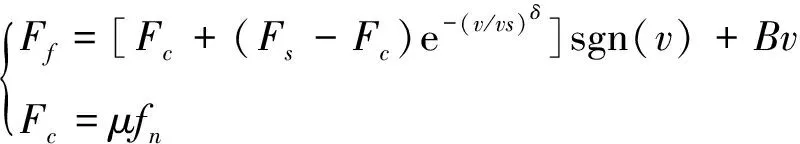
(9)

式中:B为黏滞摩擦因数;Fc为库仑摩擦力;Fs为最大静摩擦力;v为滑块的运动速度;vs为Stribeck速度;δ为经验常数;μ为摩擦因数;fn为法向力。

2.3 直线进给系统动力学模型与仿真

直线进给系统的动力学模型主要分为伺服系统和机械结构两部分。伺服系统采用PID三环控制,其中位置环采用比例控制,其比例增益为Kp;速度环与电流环采用比例-积分控制,其比例增益与积分时间常数分别为(Kv,τv)和(Ki,τi),具体控制参数如表2所示。

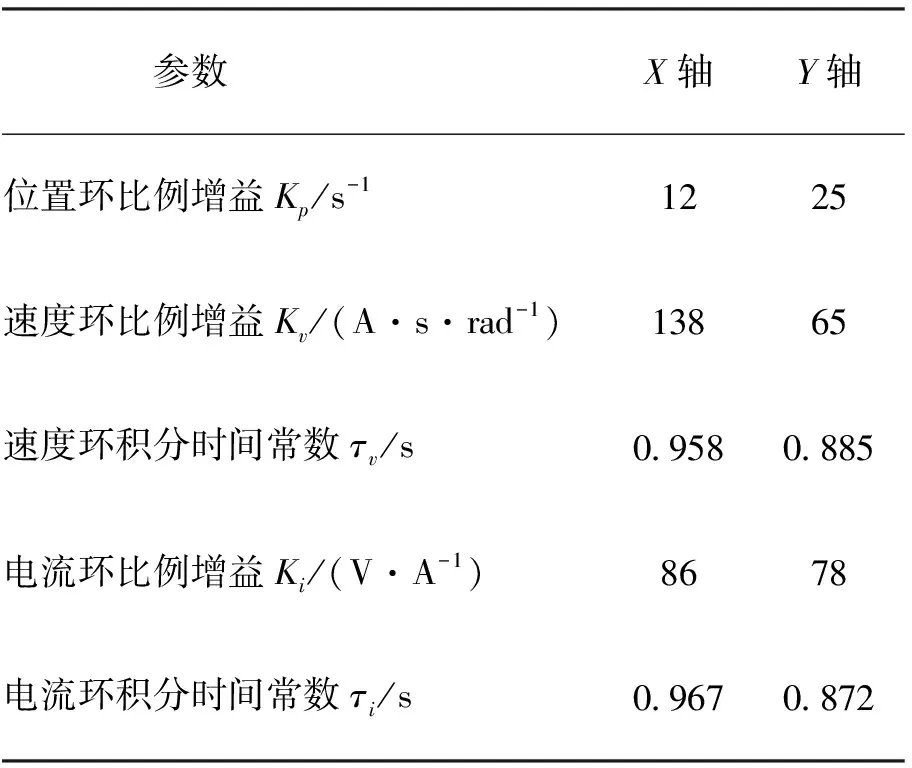
表2 PID三环控制参数

根据直线进给系统结构及伺服系统与机械结构间的输入输出关系,建立如图5所示的刚柔耦合动力学模型。其中:x*、θ*、ω*为位置、角度和速度指令;i*、u*为控制电流和电压;ωm为电机的输出角速度。

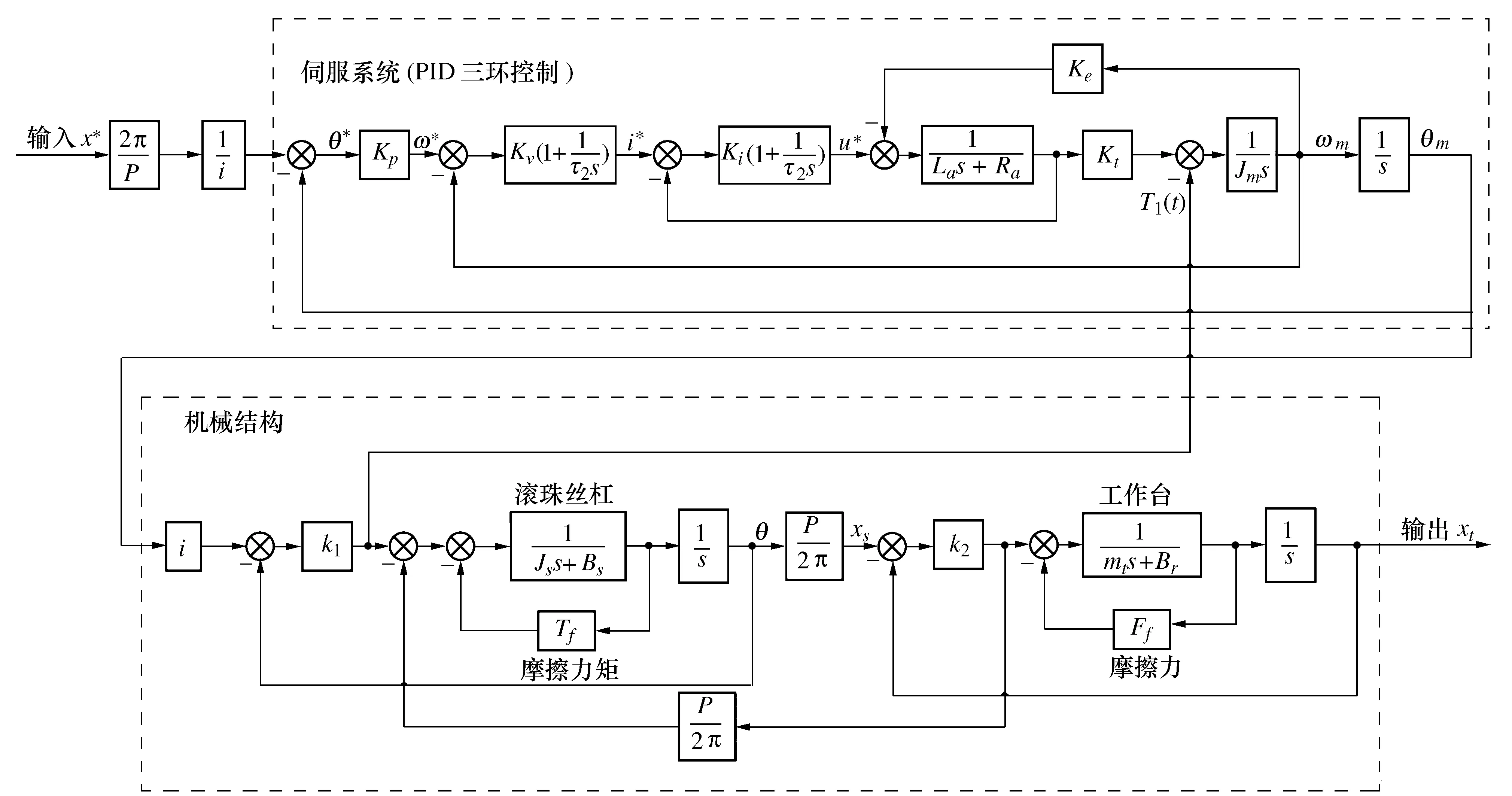
图5 直线进给系统的刚柔耦合动力学模型

在MATLAB/Simulink环境下,基于上述动力学模型进行XY两轴联动圆轨迹仿真。X轴和Y轴的输入信号为

(10)

式中:R为圆半径;t为时间;改变ω值可表示不同进给速度。

图5所示的动力学模型可综合反映由机械结构和伺服系统两部分引起的动态运动误差。在100 mm/min、300 mm/min、500 mm/min这3种不同进给速度下进行仿真,可得到总动态运动误差,如图6a)所示,其总体趋势呈三角函数变化,它们的误差变化区间分别为[-67 μm,+60 μm]、[-81 μm,+72 μm]和[-95 μm,+82 μm],且随进给速度的增大而增大。

单独仿真运行伺服系统部分,可得到由伺服系统引起的动态运动误差,结果如图6b)所示。在3种不同的进给速度下,其误差变化区间分别为[-15 μm,+15 μm]、[-16 μm,+16 μm]和[-18 μm,+18 μm],最大变化量仅为3 μm。

将总动态运动误差(图6a))减去由伺服系统引起的动态运动误差(图6b)),即可得由机械结构引起的动态运动误差(图6c))。对比图6a)～图6c)这3幅图可发现,由机械结构引起的动态运动误差占总动态运动误差的75%以上。由此可见,由机械结构引起的动态运动误差对总动态运动误差起主导作用。

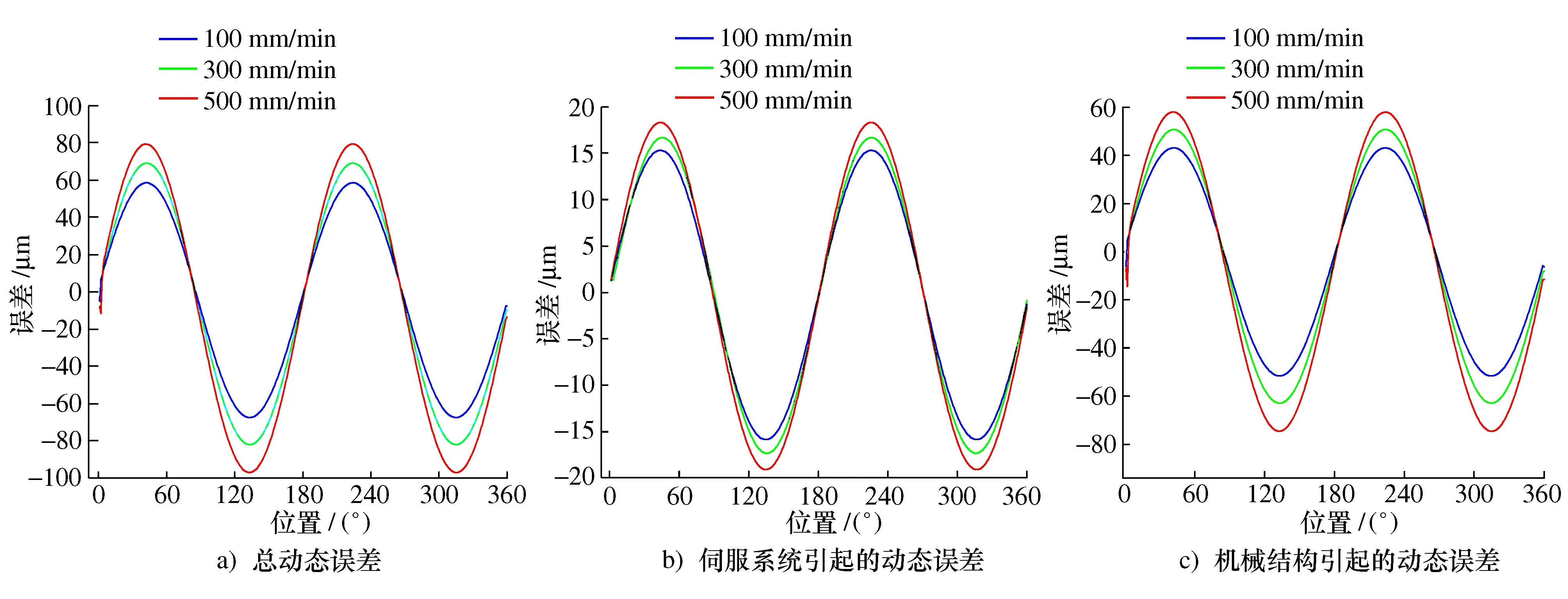
图6 基于圆轨迹的动态运动误差仿真结果

3 实验验证

3.1 圆试件切削

在一台三轴VMC850E数控立式加工中心上开展实验。试件的原材料为205×205×20 mm的铝合金,经去毛刺、清洗后装夹到机床工作平台夹具上。实际切削工艺参数如下:3种不同进给速度100 mm/min、300 mm/min、500 mm/min,主轴转速1 200 r/min,圆试件半径100 mm,切深5 mm。加工完成后的工件如图7所示。

图7 实际切削圆试件

3.2 三坐标测量机标定

如图8所示,在圆试件的圆周上均匀选取72个点,对其进行三坐标标定,可得3个圆试件的总加工误差如图9所示。在3种不同的进给速度下,其误差变化区间分别为[-26 μm,+20 μm]、[-30 μm,+24 μm]和[-36 μm,+27 μm]。3种不同进给速度下的圆试件的总误差曲线形状基本相同,且随速度的增大而增大。

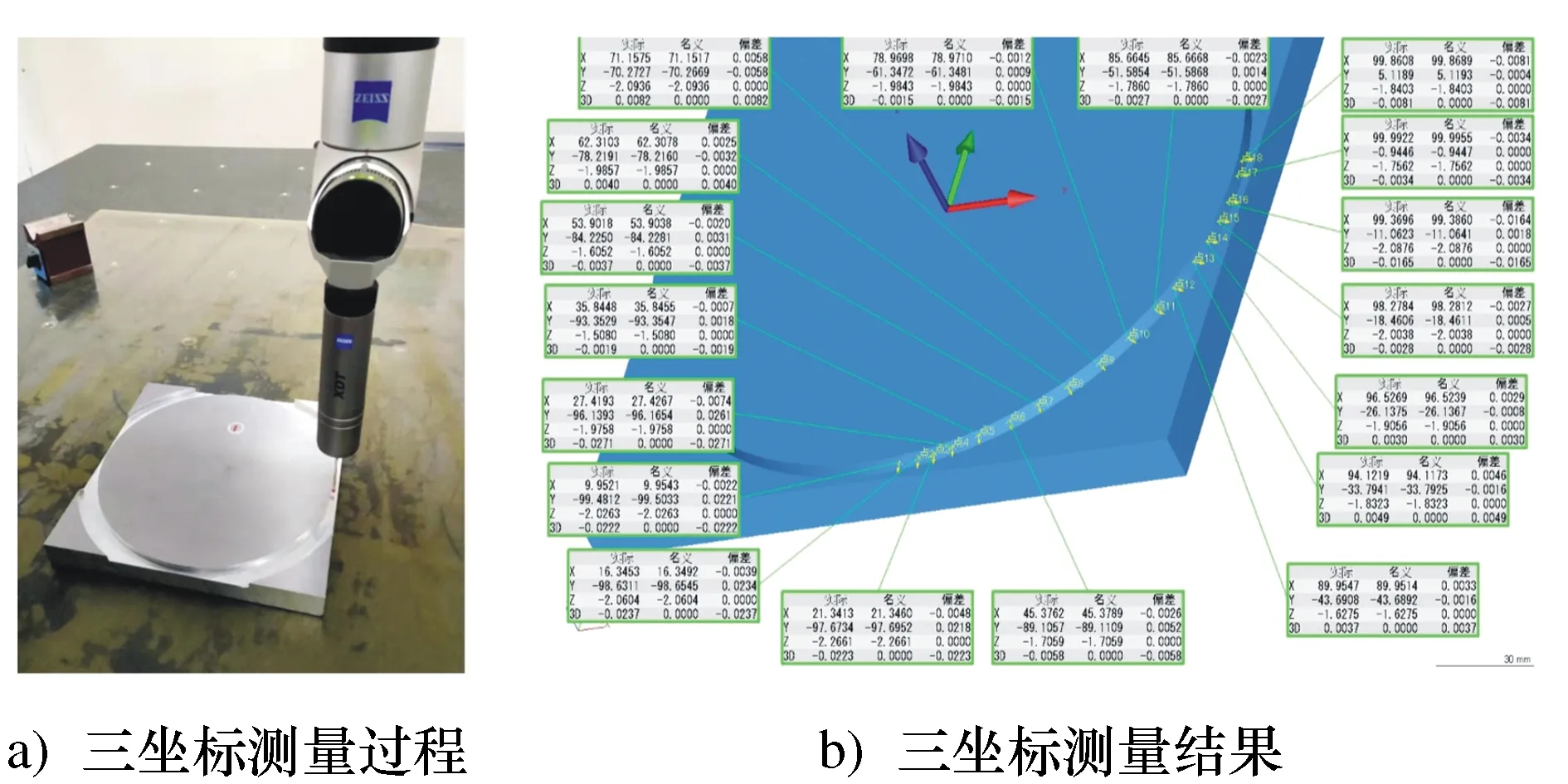
图8 三坐标标定过程

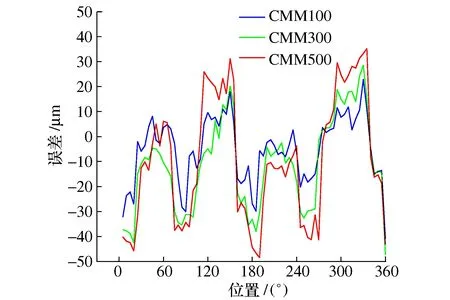
图9 三坐标机标定的圆试件总误差

3.3 球杆仪圆测试

如图10a)所示,在机床空载状态下,以进给速度(100 mm/min、300 mm/min、500 mm/min)在XY平面进行半径为100 mm的球杆仪圆测试。球杆仪圆测试误差可视为机床的静态运动误差(几何误差)与由伺服系统引起的动态运动误差之和。测试过程中,球杆仪在XY平面中运行的位置与圆试件切削时刀具运动位置相同,从而保证两者静态运动误差的影响相同,方便分析由伺服系统引起的动态运动误差。

球杆仪测试结果如图10b)所示,其误差变化区间为[-90 μm,+83 μm],不同进给速度下的3组测试得到的误差基本相同,最大变化量仅为2 μm。此外,本次球杆仪实验还测试了进给速度分别为800 mm/min、1 000 mm/min、1 200 mm/min、1 500 mm/min、1 800 mm/min时的误差,测试结果见表3。同样,在这五组不同的进给速度下,圆测试结果几乎不随进给速度的变化而变化,最大变化量仅为2 μm。

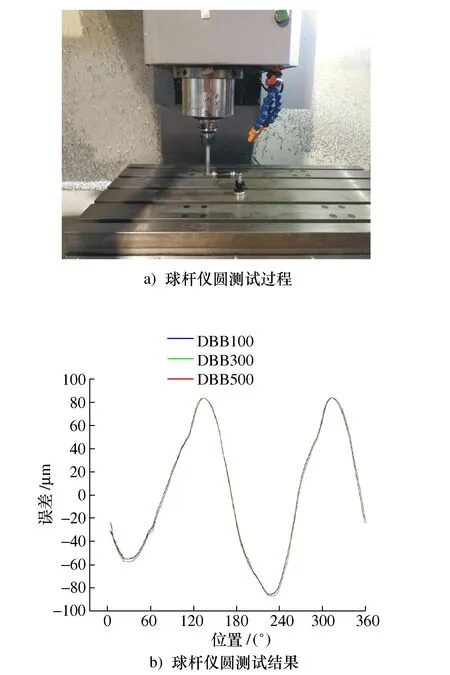
图10 球杆仪测试

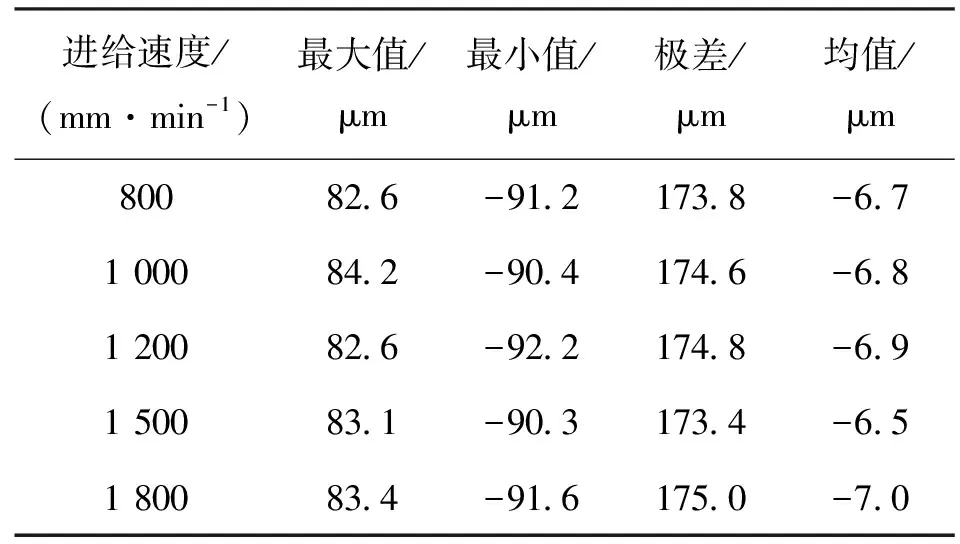
表3 不同进给速度下球杆仪圆测试的结果

由于球杆仪测试得到的误差是由机床的静态运动误差和伺服系统引起的动态运动误差两部分组成,而静态运动误差在机床的相同位置一般为恒定值,所以,不同进给速度下,由伺服系统引起的动态运动误差的变化不大。因此,可认为不同进给速度下,工件总误差的变化主要来自于由机械结构引起的动态运动误差。

4 动态运动误差溯源

将三坐标标定值(图9)减去球杆仪圆测试结果(图10b)),即为由机械结构引起的动态运动误差,如图11所示。由机械结构引起的动态运动误差的整体变化趋势大致呈三角函数规律,它们的误差变化区间分别为[-70 μm,+70 μm]、[-80 μm,+80 μm]和[-85 μm,+85 μm]。由此可见,随着进给速度的增大,由机械结构引起的动态运动误差逐渐增大。

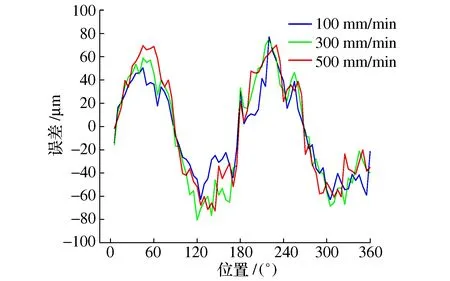
图11 由机械结构引起的动态运动误差

将仿真结果(图6c))与实验结果(图11)中的由机械结构引起的动态运动误差进行对比,得到如图12所示的结果,两者的吻合度可根据精度公式计算，即

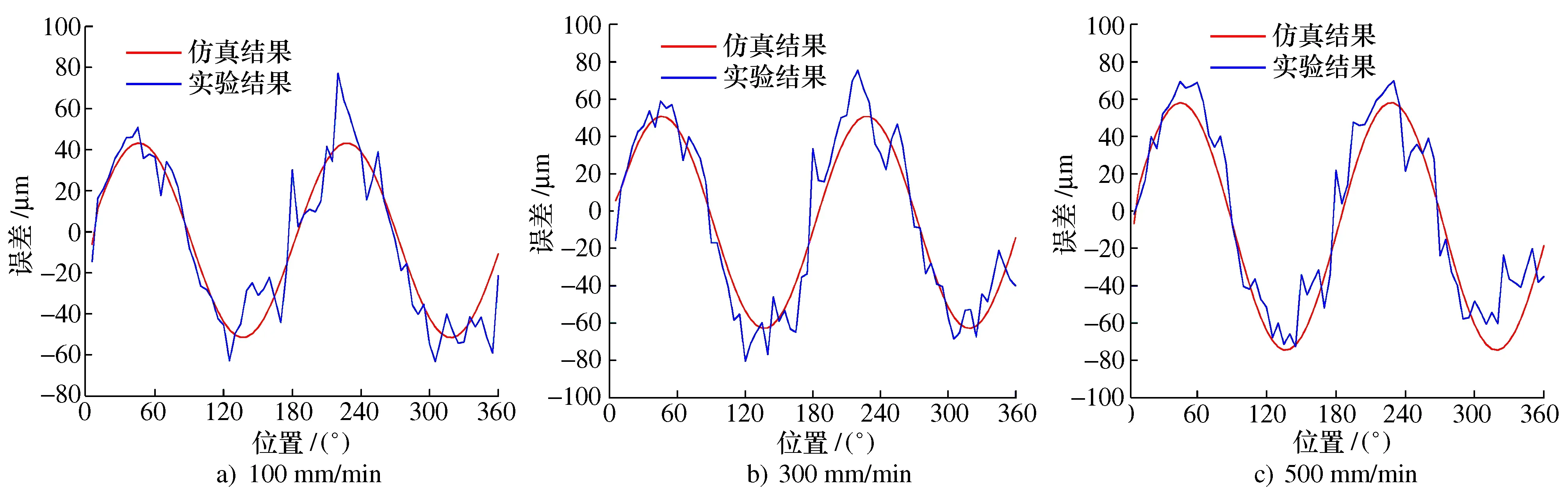
图12 不同进给速度下由机械结构引起的动态运动误差的实验与仿真结果对比

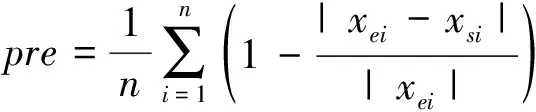
(11)

式中:xei为第i组实验数据;xsi为第i组仿真数据;n为样本个数。

3组实验与仿真曲线的吻合度分别为72.3%、76.8%、71.5%,由此验证了动力学模型的准确性。

5 结论

本文通过不同进给速度下切削圆试件,并基于三坐标标定与球杆仪圆测试分离了由机械结构引起的动态运动误差。同时建立了机床进给系统的机电刚柔耦合动力学模型,溯源了两轴联动时的动态运动误差,得到以下结论:

1)直线进给系统的动态运动误差由伺服系统和机械结构两部分决定,其中由机械结构引起的动态运动误差在总动态运动误差中占主导作用;

2)在机床空载的状态下,球杆仪圆测试结果几乎不随进给速度的增大而改变,即进给速度的变化对由伺服系统引起的动态运动误差影响不大;

3)基于机电-刚柔耦合特性分析的动力学模型可准确分析数控机床直线进给系统的动态运动误差。

以上结论可为数控机床直线进给系统的动态运动误差分析和补偿奠定理论基础。