探索式服务组合中的增量式失败服务模式挖掘
袁云静,王 菁,韩燕波,栗倩文,陈高建,焦博扬
(北方工业大学 大规模流数据集成与分析技术北京市重点实验室,北京 100144)
0 引言
随着服务计算、云计算、物联网、大数据等高新技术的快速发展与成熟,各个服务行业与领域涌现出大规模智能服务,人们的生活越来越依赖于互联网提供的服务[1-2],而服务系统中的细粒度原子服务难以满足日益复杂的用户需求。因此,服务组合受到科研人员的持续关注。在求解科研协作、远程医疗、城市应急等应用领域问题过程中,服务组合逻辑往往难以预先定义完备,需要在用户参与过程中不断调整,支持边执行边构造的探索式服务组合[3]应运而生。在探索式服务组合过程中产生了大量的服务组合流程,充分利用这些历史数据可以增强服务组合流程的可重用性,提高服务组合效率。
通过分析总结探索式服务组合形成的服务组合流程,发现用户选择服务具有一定共性,某些服务经常共同出现在一个服务组合流程轨迹中,这些固定搭配的服务往往以子片段的形式出现,表现出粒度大、复用性高等特征,文献[4]将这种被高频使用的服务搭配称为服务模式。由于探索式服务组合流程的执行轨迹分为两种,其对应的服务模式也分为成功服务模式和失败服务模式两种,将这两种服务模式应用于探索式服务组合,一方面可以提高用户构造服务组合流程的效率,另一方面可以充分利用领域先验知识,提高服务组合流程的可重用性。而当前工作大多只关注成功服务模式的挖掘,尚未有对失败服务模式挖掘的研究,相应历史数据的价值没有得到充分发挥。如果将成功服务模式的挖掘方法直接运用于失败服务模式的挖掘,会造成不必要的时间与资源浪费,原因是在流程轨迹中,只有一部分流程片段最终导致执行失败,而非整个轨迹都是失败的,因此将挖掘聚焦于失败部分可提高挖掘效率。
针对上述问题,本文提出探索式服务组合流程实例建模及服务模式建模方法,设计了一种扩展gSpan算法的增量式失败服务模式挖掘算法(Incremental Failure Service Pattern Mining Algorithm, IFSPMA),通过所提模型与算法,可增量式地挖掘出服务组合流程执行失败轨迹中的失败服务模式,实验表明,相比原始算法,IFSPMA明显提高了挖掘效率。
1 相关工作
1.1 基于日志的服务模式挖掘
基于日志的服务模式挖掘算法主要有4种:
(1)α及其扩展算法[5]该算法扫描日志中的所有实例,抽象活动之间的基本关系,根据基本关系的类型直接构造流程的控制流结构,其虽然能够处理各种控制流结构,但是无法处理日志中的噪声。
(2)启发式算法[6]该算法主要考虑流程实例在日志中出现的频率,其虽然既可以挖掘流程的主要行为,也可以处理日志噪声,但是忽略了流程细节,而且无法处理日志多样性并进行质量监控。
(3)遗传算法[7]该算法是一种模拟生物进化过程的搜索技术,能够同时处理各种控制流结构和日志噪声,但可能得不到最优的流程模型。
(4)基于日志分类的算法 该算法对日志中的执行实例进行聚类[8],将日志划分为多个子日志,借助已有挖掘算法对子日志进行挖掘,该算法能够很好地处理日志的多样性,但是依赖现有具体挖掘算法。
1.2 基于流程的服务模式挖掘
基于流程的服务模式挖掘可抽象为频繁子图挖掘,其解决方式主要采用Apriori算法和FP-growth算法两种算法思想。
应用Apriori思想的挖掘算法有基于Apriori的图挖掘(Apriori-based Graph Mining, AGM)算法[9]和基于该算法的改进算法,AGM算法思路简单,以递归统计为基础,可挖掘出所有频繁子图,但对大型数据库的执行效率较低。其改进算法有频繁子图(Frequent Subgraph, FSG)算法[10]和基于Apriori的连通图挖掘(Apriori-based connected Graph Mining, AcGM)算法[11],这两种算法的执行效率较AGM算法均有提高。文献[12]采用Apriori算法思想设计了一种辅助服务组合发现的挖掘算法。
FP-growth算法[13-14]将数据压缩到频繁模式树中,存储项的关联关系,然后对模式树产生频繁集,其因为无需产生候选频繁集,所以执行效率高于Apriori算法。基于这一算法思想的频繁子图挖掘算法包括gSpan算法[15]、快速频繁子图挖掘(Fast Frequent Subgraph Mining, FFSM)算法[16]等,其中gSpan算法的最右路径扩展与频繁剪枝策略,大幅降低了算法运行时间;FFSM算法在计算支持度时,只对embedding set进行扫描,提高了计算速度与效率,但其无法支持有向图的挖掘。LIU等[17]借助FP-growth算法思想从历史服务组合挖掘服务模式来研究服务选择算法优化。
以上服务模式挖掘的相关工作均是针对构建成功的服务组合流程的挖掘方法,尚未考虑文献[18]探索式服务组合中带有调试点的失败流程轨迹,且其挖掘往往针对整个服务组合流程,易对时间与资源产生不必要的浪费。因此,本文综合考虑当前服务模式挖掘的特点及其存在的问题,采用基于流程的服务模式挖掘算法,鉴于这类可选算法的挖掘效率及可实现性,最终选择基于gSpan算法进行改进,以支持对包含调试点的失败服务模式的挖掘。
1.3 增量式更新
增量式更新的相关工作主要有增量式关联规则挖掘、增量式频繁子图挖掘。FENG等[19]针对原始数据库不变、最小支持度和置信度改变时,如何生成新的关联规则,提出增量式更新算法(Incremental Updating Algorithm, IUA)和并行增量式更新算法(Parallel Incremental Updating Algorithm, PIUA);CHEUNG等[20]针对最小支持度和置信度不变、数据库发生改变时,如何生成新数据库的关联规则,提出快速更新(Fast Update, FUP)算法;XU等[21]研究在原始数据与最小支持度、置信度同时发生变化时关联规则的更新问题;CHAE等[22]对频繁子图挖掘算法gSpan进行了增量式挖掘,将增量式gSpan应用于动态图包分类,并随时间推移逐步更新top-m最具辨别力的特征。虽然当前增量式更新已有较多研究,但是尚未发现在服务领域的应用。本文结合所使用的失败服务模式挖掘算法,在文献[22]增量式gSpan研究的基础上进行改进,使其适应服务模式挖掘的应用环境。
2 服务模式模型
本章主要对探索式服务组合实例及服务模式进行形式化建模。
2.1 探索式服务组合实例模型
探索式服务组合可支持业务用户对不完备的服务组合流程进行边执行边构造,在构造执行过程中遇到执行结果不正确或中间产生数据不满意的情况时,可在相应节点处添加调试点,派生新的轨迹,然后继续构造,直到探索出一条可完成目标任务的成功路径。探索式服务组合实例模型如图1所示。

定义1探索式服务组合实例。探索式服务组合实例表示为一个三元组Instance=instanceID,name,trackSet,描述通过服务组合流程实例实现某些目标的探索性过程。其中,instanceID为探索式服务组合实例的唯一标识符;name为探索式服务组合实例的名称;trackSet为实例中包含的轨迹集合。
定义2轨迹。轨迹表示为Track=trackProfile,instanceID,status,activities,transitions,directDeriv,dataPocket,exploredState,其中:trackProfile为轨迹基本信息,包括trackID,name,createTime等;instanceID为轨迹所属实例;status为轨迹的执行状态,status∈{init,running,suspend,complete,terminated};activities为轨迹中包含的活动;transitions为轨迹中所包含活动间的变迁关系;directDeriv在派生关系中定位原始轨迹,directDeriv=originalTrack,probePoint,originalTrack标记当前派生轨迹的父轨迹,probePoint标记派生时原始轨迹中的调试点(添加调试点操作参见定义5,派生关系参见定义6);dataPocket为轨迹执行产生的数据信息;exploredState为探索完成后的轨迹状态,exploredState∈{success,failure}。
定义3活动。活动表示为Activity=activityID,activityName,Input,Output,QoS,type,status,其中:activityID为活动的唯一标识;activityName为活动名称;Input为输入参数集合;Output为输出参数集合;QoS为活动质量;type为活动类型,type∈{service,start,end,orSplit,orJoin,andSplit,andJoin};status为活动执行状态,status∈{init,running,suspend,executed}。
定义4变迁关系。变迁关系表示为Transition=tranID,fromAct,toAct,dataMappingSet,其中:tranID为变迁关系的唯一标识;fromAct为变迁关系源活动;toAct为变迁关系目标活动;dataMappingSet为源活动和目标活动之间的数据映射关系集合,每个数据映射可表示为dataMapping=SourcePara,TargetPara,mappingExpression,SourcePara为源节点的输入和输出参数的集合,TargetPara为目标节点的输入参数的集合,mappingExpression为SourcePara和TargetPara之间的参数映射关系表达式。
定义5添加调试点操作。添加调试点操作记为addProbePoint(pt,a),其中pt为轨迹,a为活动,只有pt的状态不是terminated且a的状态为executed,才允许添加调试点。该操作会生成新的轨迹pt′,其变迁关系的dataMappingSet及调试点a的前继活动均从原始轨迹克隆且保持不变,调试点a及其后继活动克隆后重置初始化。
定义6派生关系。派生关系是一个二元单向关系dr(tr1,tr2),其中tr1为原始轨迹,tr2为派生轨迹。如果两个流程片断分别表示流程轨迹tr1和tr2中从开始节点的可达流程片断,满足:①流程片断中活动的名称、输入输出参数,以及参数值、类型等完全相同,且状态均为executed;②流程片断中变迁关系的源活动、目标活动及活动之间的数据映射关系完全相同。则称这两个可达流程片断相同。如果两个轨迹共享相同的可达流程片段,则其为派生关系,其中createTime较小的轨迹为原始轨迹,另一个为派生轨迹。
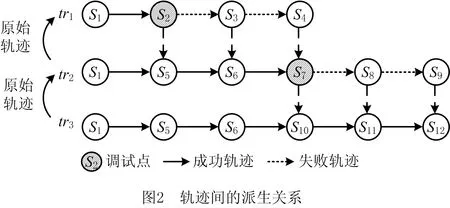
轨迹间的派生关系如图2所示,包括3条轨迹tr1~tr3和12个服务节点S1~S12,其中:tr1为原始轨迹,S2为原始轨迹中的调试点,从该点派生出轨迹tr2,片断S1为原始轨迹tr1和tr2的相同可达流程片断;以tr2为原始轨迹,S7为调试点,派生出轨迹tr3,片断S1→S5→S6为其相同的可达流程片断。
2.2 服务模式模型
探索式服务组合实例执行完成后,可确定成功流程轨迹与失败流程轨迹,对这两种轨迹进行挖掘可得两种不同的服务模式。
定义7服务模式。服务模式表示为SP={spID,activities,transitions,type},其中:spID为服务模式唯一标识;activities为服务模式包含的活动;transitions为活动间存在的变迁关系;type为服务模式的类型,type∈{success,failure}。
3 增量式失败服务模式挖掘算法
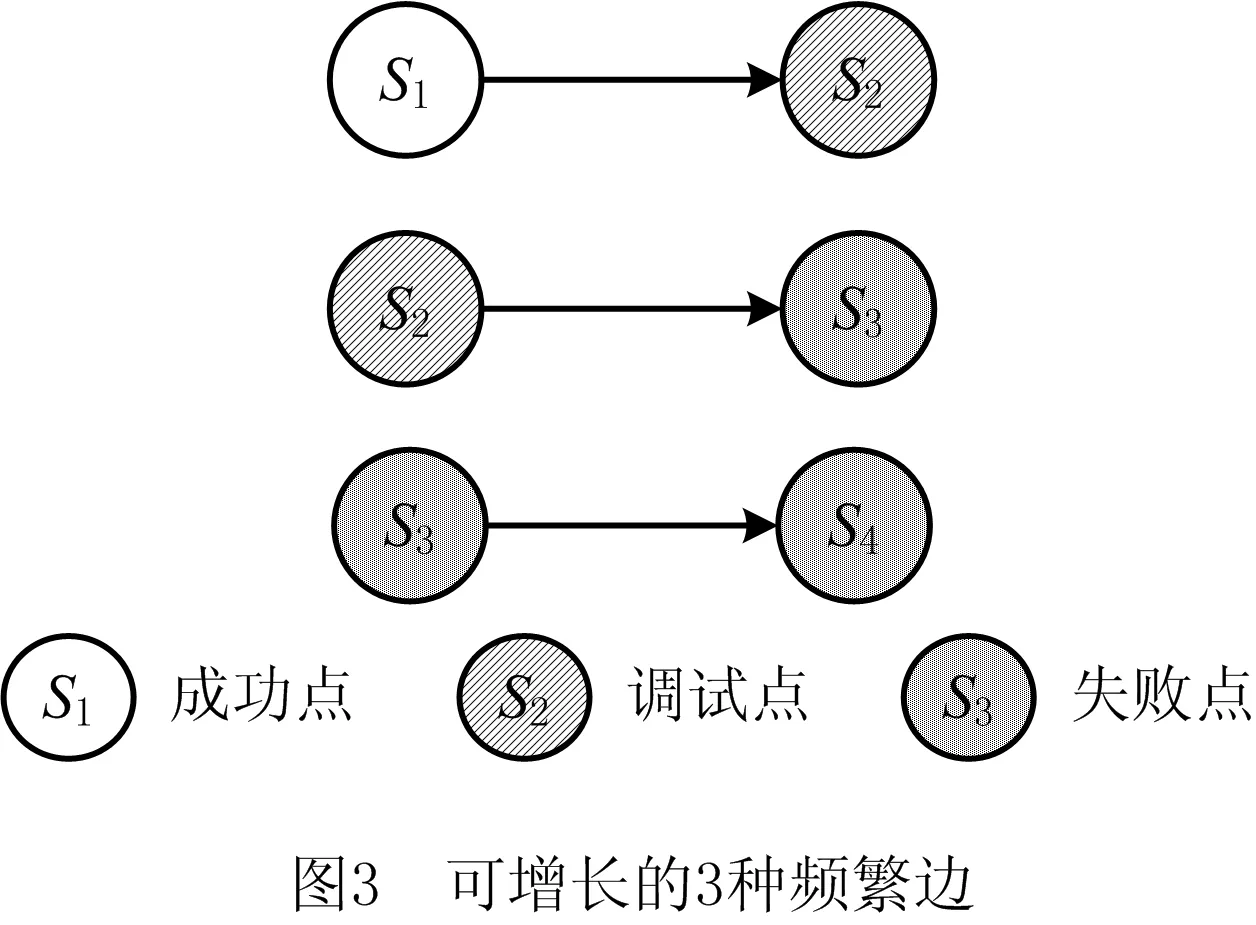
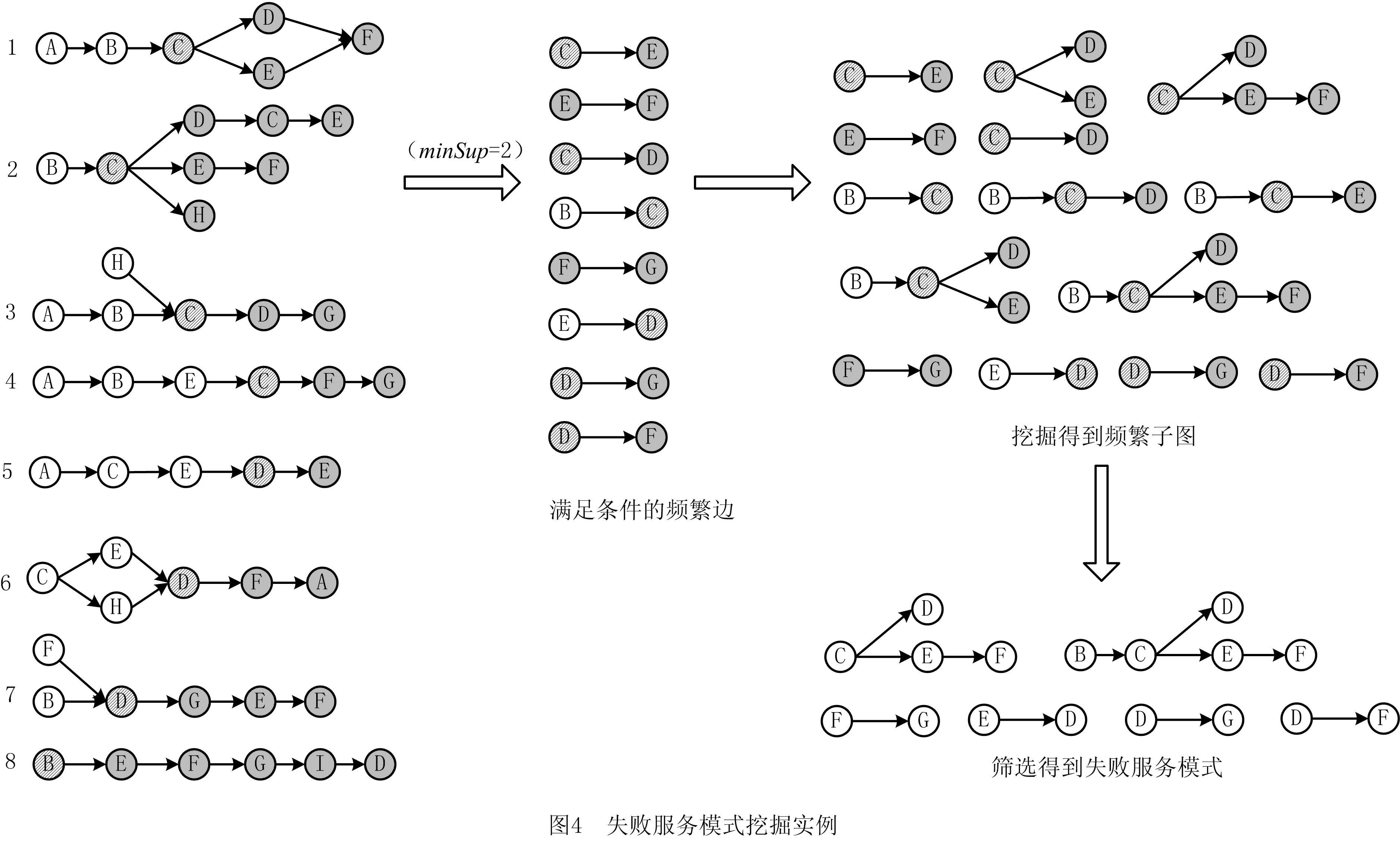
为了从服务组合流程的失败流程轨迹中挖掘出失败服务模式,并适应服务组合流程数量不断增加的探索式服务组合环境,本文提出IFSPMA,该算法将挖掘范围限定在调试点附近,对执行失败的轨迹进行挖掘。首先将输入的失败流程轨迹集T抽象为图集P,将轨迹上调试点前面的顶点标记为成功点,调试点后面的顶点标记为失败点(算法1第1行);然后基于频繁度对P中的顶点与边排序,删除非频繁顶点与边(算法1第2~3行),将剩余频繁边以深度优先搜索(Depth First Search, DFS)的字典序排序(算法第5行);最后,为挖掘得到失败服务模式,要求频繁子图中必须包含至少一个调试点或失败点,因此仅针对图3中的3种频繁边进行Subgraph_Mining最右路径扩展挖掘(算法第8行),将扩展后形成的DFS编码树作为中间结果保存,用于后续增量式挖掘。完成一条边的扩展挖掘后,从原图删去挖掘过的这条边(算法第12行),继续扩展挖掘下一个满足条件的频繁边的子图,重复该过程,直到遍历完所有满足条件的频繁边。该过程实例如图4所示。
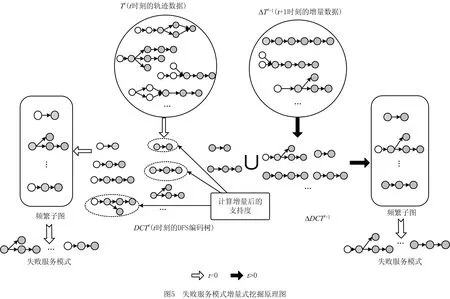
IFSPMA的增量式挖掘部分介绍如下:如果当前服务库中不存在服务模式,如图5所示的t=0时刻算法过程,将DFS编码树中支持度大于minSup的节点作为频繁子图输出,并经筛选得到失败服务模式存入服务库;如果当前服务库中已有服务模式(算法1第15行),则合并当前时刻(假设为t+1时刻)增量DFS编码树与t时刻DFS编码树,将同时存在于两棵树中的节点支持度相加作为t+1时刻该节点的支持度,将仅存在于t+1时刻增量DFS编码树与仅存在于t时刻DFS编码树中的节点直接拷贝到t+1时刻DFS编码树中(算法1第16~21行);最后,根据minSup对DFS编码树进行剪枝得到所有频繁子图(算法1第22~24行),筛选后得到失败服务模式。
该失败服务模式增量式挖掘原理图如图5所示。
算法1IFSPMA。
输入:轨迹集T、t时刻的DFS编码树t_dct、最小支持度minSup。
输出:失败服务模式集合FS。
1: 将T抽象为图集P并标记成功点与失败点;
2: 通过频繁度对P中的顶点与边进行排序;
3: 移除非频繁顶点与边;
4:FS1←P中的频繁1子图;
5: 以DFS字典序为FS1排序;
6:FS←FS1;
7: for FS1中的每条边e do
8: if e.from和e.to均为失败点
or e.from为调试点,且e.to为失败点
or e.to为调试点:
9: incremental_dct←incremental_dct∪{e};
10: 初始化s为e, 设置s.P为包含e的图集;
11: FS←Subgraph-Mining(P,FS,s,minSup);
12: P←P-e;
13: if |P| 14: break; 15:if t_dct不为空: 16: for increment_dct中的每一个DFS编码c do 17: if c在t_dct中: 18: 重新计算c.support,并将更新后的c写入t1_dct中; 19: else: 20: 直接将c写入t1_dct中; 21: 将t_dct中剩余的DFS编码写入t1_dct中; 22: for t1_dct中的每一个DFS编码c do 23: if c.support >=minSup: 24: FS←FS∪{c}; 25:FS←FS中的频繁闭子图; 26: return FS 子过程调用1子图挖掘。 输入: 图集P、频繁子图集合Q、频繁片段s、最小支持度minSup。 输出:频繁子图集合Q。 1: if s≠min(s): 2: returnQ; 3: if t_dct不为空: 4: Q←Q∪{s}; 5: 遍历P中包含s的每个图,并扩展得到包含s的子图; 6: for扩展得到的每个子图c do 7: incremental_dct←incremental_dct∪{c}; 8: if support(c)≥minSup: 9: s←c; 10: Q←Subgraph-Mining(Ps,Q,s); 本节采用仿真实验评估IFSPMA的性能和有效性。为提高实验的可信度,本文采用myexperiment(www.myexperiment.org)研究社区爬取的1 405个流程作为实验数据集,其为该社区访问量和下载量最高的xml与t2flow格式的数据集。该社区是供全球生物计算研究者发布并共享生物计算流程及实验计划等信息的一个协作环境,学者们可以在社区中发布其流程和实验,与小组分享,也可以找到其他人的流程,从而减少实验时间,避免流程再造。 为满足算法需要,本文将收集到的生物流程文件进行解析,将服务抽象为顶点,服务名称设为顶点标签,服务之间的关联关系抽象为边,为获得更多的频繁服务模式,将统计出的最频繁的16个活动节点设为调试点。由于从网站上爬取的流程均可成功执行,本文通过程序模拟构造失败流程轨迹,共构造10 490个流程轨迹,用于IFSPMA实验验证。 仿真程序用Anaconda 3.6和Pycharm开发,运行在一台CPU为AMD Ryzen 7 2.90 GHz、内存为16 G的Windows操作系统PC机上。 实验主要观察在挖掘准确度相同时,IFSPMA相比未使用增量式更新的失败服务模式挖掘算法(Failure Service Pattern Mining Algorithm,FSPMA)及未将挖掘聚焦于调试点附近的gSpan算法挖掘效率的提升情况,3种算法的对比说明如表1所示。实验主要分析在挖掘准确度相同时,不同的最小支持度、轨迹数量、挖掘结果个数对算法运行时间的影响。 表1 算法对比说明 算法参数主要为最小支持度和轨迹数量,如图6所示,在轨迹数量固定为10 000的条件下,调整最小支持度,针对FSPMA与gSpan算法,在挖掘结果完全相同时,前者的运行时间明显低于后者,当minSup=10时,FSPMA与gSpan算法的挖掘效率均处于较优状态。 选取minSup=10,分析不同轨迹数量下的运行时间,如图7所示。当轨迹数以1 000为单位增长,挖掘准确度基本相同时(误差极小可忽略),IFSPMA的运行时间明显低于FSPMA和gSpan算法。 挖掘到的服务模式个数也可能会影响IFSPMA的运行时间,当minSup=10时,不同算法挖掘相同服务模式个数所用的运行时间如图8所示。可见,随着挖掘到的服务模式个数的增长,IFSPMA的运行时间比gSpan算法明显降低,比FSPMA算法有所降低。 综上所述,IFSPMA可有效将挖掘聚焦于生成失败服务模式,避免gSpan算法面向整个服务组合流程的挖掘方式,而且算法可适应不断增量的探索式服务组合环境。在不同的最小支持度和轨迹数量下,IFSPMA的挖掘效率较其他两种算法均有提升,其中在当前数据集下,minSup=10时,IFSPMA的效率比gSpan算法提高得最多;随着轨迹数量的增加,IFSPMA效率相比FSPMA提高的百分比稳定在40%左右,相比gSpan提高的百分比稳定在67%左右。 本文重点讨论了从执行失败的服务组合流程轨迹中增量式挖掘失败服务模式的相关研究。针对探索式服务组合的特点,为加快用户探索式构建服务组合流程的速度与准确度,同时充分利用历史服务组合流程数据,提出一种扩展gSpan算法的改进算法——IFSPMA,用于挖掘探索式服务组合流程中调试点附近失败流程轨迹的服务模式,在此基础上研究增量式挖掘,动态更新服务库中的服务模式。另外,根据问题及算法特点,定义了探索式服务组合实例模型与失败服务模式模型,作为IFSPMA的基础。通过用模拟数据集对算法进行实验评估,将IFSPMA与非增量的FSPMA算法和未聚焦于调试点的gSpan算法进行对比,验证了本文方法的有效性和实用性。 未来将研究历史服务模式的失效问题,淘汰过时的服务模式,并结合服务模式的更新迭代分析历史库中的服务模式,观察其演化趋势。4 实验
4.1 数据集与环境
4.2 实验验证

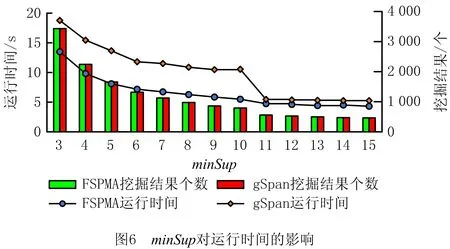
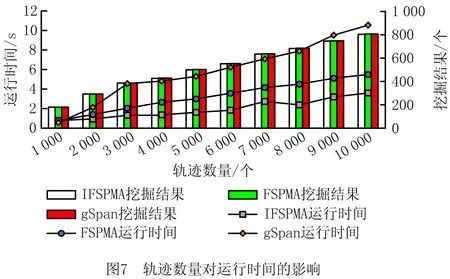
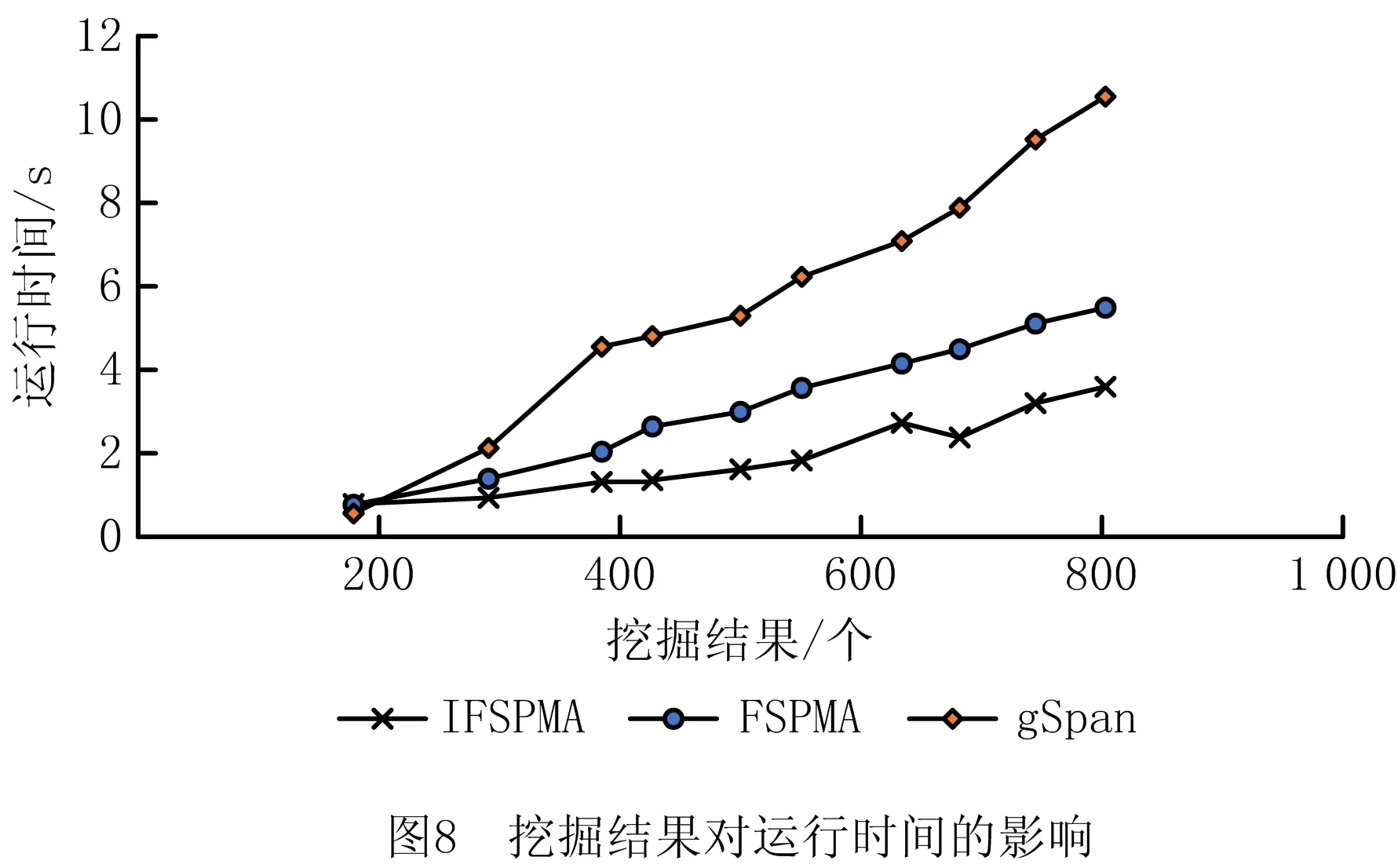
5 结束语

